基于弦测法与密度聚类的三维结构光波磨检测
2020-02-26王培俊李保庆李文涛
杨 杰,王培俊,肖 俊,李保庆,李文涛
(1.西南交通大学机械工程学院,成都 610031; 2.成都西南交大研究院有限公司,成都 610031)
钢轨波形磨耗,简称“波磨”,是指钢轨踏面沿纵向出现的一种周期性类似波浪形的不平顺现象,是城市轨道交通的主要危害之一[1-2]。严重的波磨不仅会缩短轨道的使用寿命,还会产生刺耳的噪声,甚至发生脱轨现象,产生严重的安全事故。因此,快速有效地检测波磨,及时对轨道进行维护,显得尤为重要。
波磨在钢轨的曲线、直线段皆有发生,直线段的波磨现象较轻微。其中,在轨道减振器地段,波磨波长为35~50 mm,在客货混运段的波磨波长一般为200~300 mm。地铁线路的曲线段较多,以R=350 m的小半径曲线段为代表的地段发生波磨较严重,波长一般为30~80 mm。在重载铁路上,波磨主要发生在曲线段,波长为100~600 mm[2-5]。
目前,国内外钢轨波磨检测的方法以接触式检测为主,其代表有:钢轨波磨仪、德国的RMF1100、惯性法等。其中,波磨仪采用弦测法,属于静态检测,仅适用于短距离短时间测量。RMF1100利用测量头与钢轨踏面接触获取踏面数据,计算得到波磨信息,属于动态检测[6]。惯性法是在轨检车车体安装加速度传感器,得到模拟波形来表征实际波形,但轨检车费用昂贵,且不能达到理想的检测精度[7-9]。近年来,国内学者在非接触式检测上进行了大量研究,马子骥等提出的基于多线结构光视觉的钢轨波磨动态测量方法[10],但校正、提取轨鄂点、配准都存在误差,导致精度难以满足波磨高精度检测的要求。李清勇等提出基于钢轨图像频域特征的钢轨波磨检测方法,从频域空间中基于频率阈值和能量阈值判定波磨线,对连续区间的频率和能量进行判断,从而识别波磨图像[11]。但波磨的多样性令该方法仅能识别周期性非常明显的波磨,大部分的波磨可能被忽略。李坪等提出应用三维结构光和小波分析进行波磨检测[12],应用香农采样定律和小波分析计算波磨,由于采样随机性大且波磨复杂多变,有可能导致结果不准确。
为有效地检测波磨,提出综合利用三维结构光技术、弦测法和密度聚类算法的波磨检测方法,实验室样件试验及现场试验结果均较为理想。
1 波磨检测系统方案设计
基于光学三角形测量原理的三维结构光检测系统,由光栅投射仪、两个成一定夹角的摄像头和计算机系统构成了三维结构光双目视觉检测系统,如图1所示。
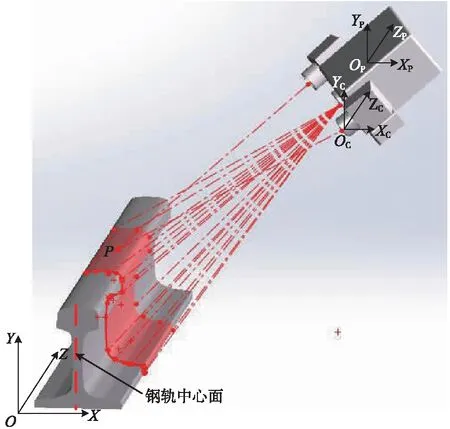
图1 三维结构光检测示意及原理
测量时,将该系统搭载在检测小车平台上,将调制后周期变化的光栅条纹投射到被测钢轨表面,光栅条纹随钢轨的形貌特征发生畸变。光栅条纹呈周期性变化,其相位也在不断地移动,计算其相位的偏移量,便可通过相位计算得到物体表面的三维信息[13]。波磨检测方案如图2所示。

图2 检测方案
2 平面遍历弦测法与密度聚类分析
如前所述,波磨常发生于轨道的曲线段[14],当取1 m长、R=350 m曲线段钢轨作为研究对象时,其所对应的弧度角为
θ=360°/(2πR)=0.164°
(1)
由弧度角引起1 m钢轨起始两端轨头中心线的偏差为
Δc=R-R·cos(θπ/180°)=4.368×10-4mm
(2)
由上述计算可知Δc的大小可忽略不计,可将曲线段钢轨分为若干1 m长的钢轨与标准直线钢轨进行配准(1 m钢轨包含了常见波磨的若干个波峰和波谷)。
2.1 纵向平面遍历
2.1.1 遍历区间
本研究的数据处理对象为钢轨点云,计算的基础是点之间的欧式距离,设Pi(xi,yi,zi)和Pj(xj,yj,zj)是点云中的两点,其对应欧式距离L2为
(3)
纵向平面遍历实质是从钢轨轨头遍历区域一侧开始,建立平行于钢轨中心面,且垂直于轨头截面的平面Si(x=Mi,i∈0,1,2,…,N) ,形成y-z平面簇;然后确定一个平面阈值VS,计算轨头各个数据点Pk(xk,yk,zk)到Si的距离,满足式(4)的点则视为平面Si对应钢轨截面的点。
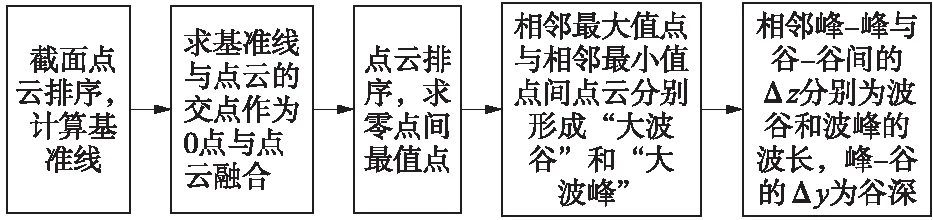
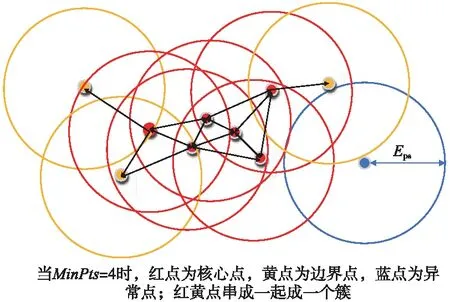
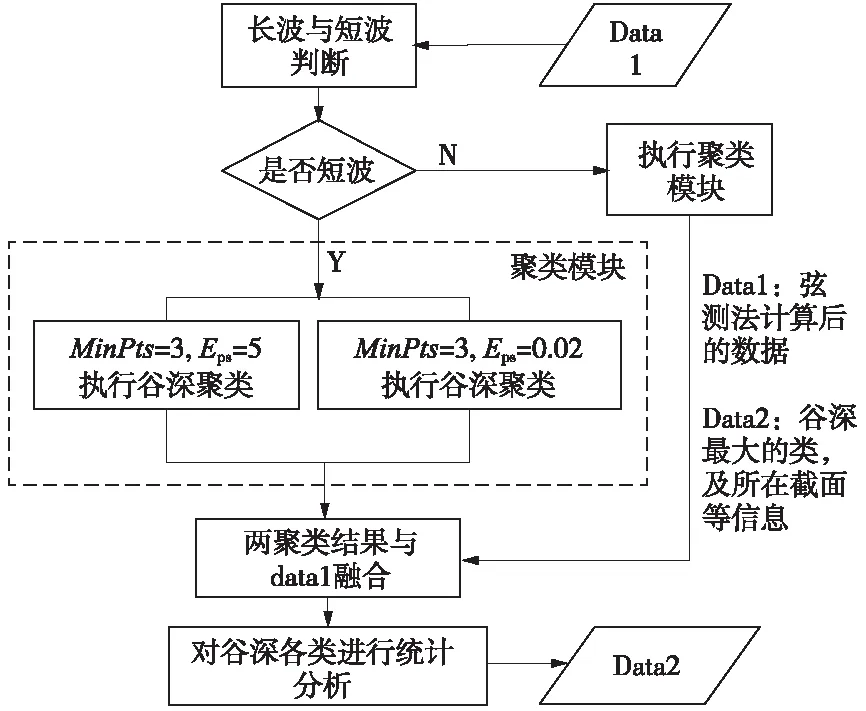
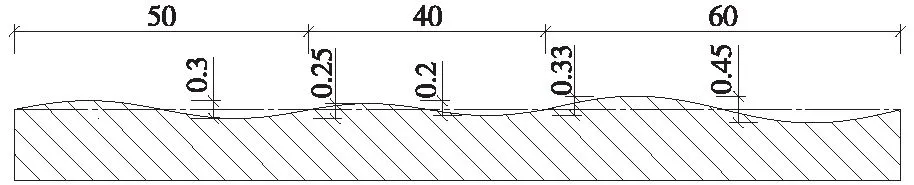
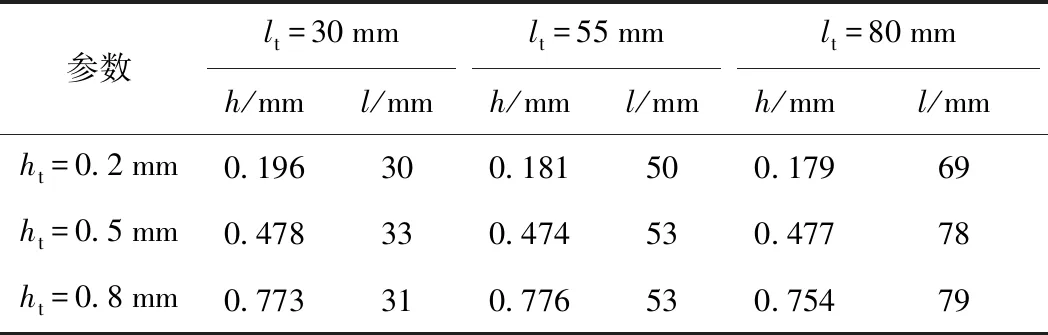
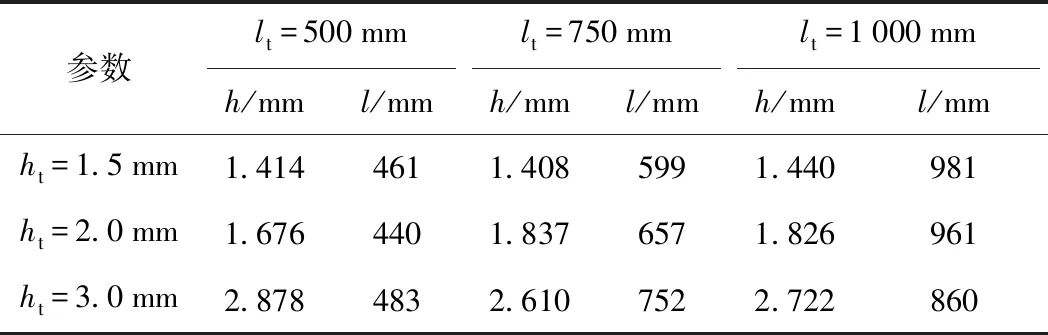
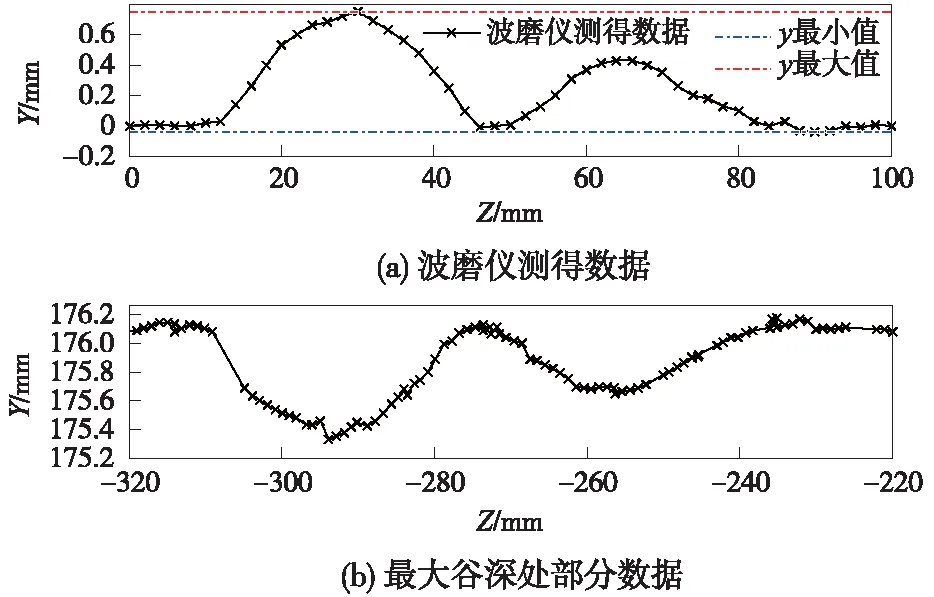
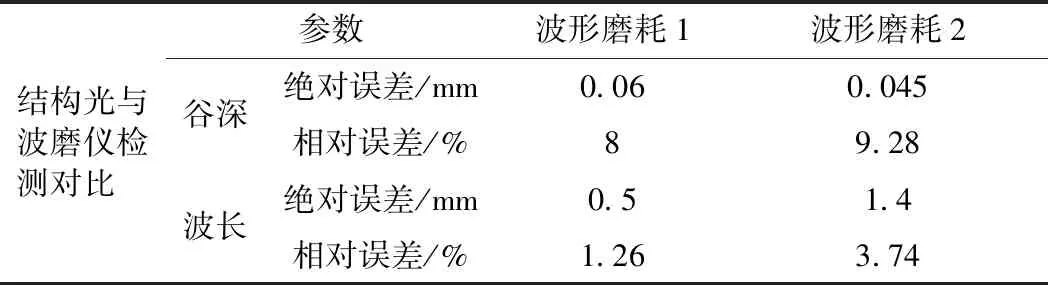
|xk-Mi| (4) 采用接触式D&F160312钢轨波磨仪进行对比试验,其测量头的位置PV距钢轨中心面的横向距离约为15 mm。进行平面遍历计算时,须将该测量点包含在遍历区域内,选取轨头距钢轨中心面20 mm内的轨顶区域为平面的遍历区域。 2.1.2 平面阈值与平面间距 平面阈值VS的大小与各平面遍历取点时,每个对应纵向截面上所包含点的数量有关。采样后,邻近点的间距约1 mm,钢轨纵向截面沿Z方向步进取点时,为保证步进内的点更接近截面,在该采样半径下需保证VS≤1 mm。 在实验室采集一段钢轨的点云,采样配准后进行平面遍历,当VS分别取0.2,0.5,0.8,1.0 mm时,得到的截面点云个数分别为100,250,350,450,其轨顶某截面轮廓如图3所示。当VS=0.8 mm时,邻近点之间间距接近采样半径。 图3 轨顶某纵向截面在不同VS下的轮廓 为尽可能将遍历区域内点云用于计算分析,遍历平面间距VI应与平面阈值VS相匹配。当VS=0.8 mm,VI=1.0 mm,遍历得到37个截面,遍历点数约13 000,采样后遍历区域内的点数约15 000,遍历区域内的点云得到充分利用。 工务部门检测波磨常用的设备为波磨仪,其检测原理是基于静态弦测法[14],每次检测前需先调零标定以保证精度。操作流程是:将波磨仪平直固定在轨顶→轨顶某点进行调零→移动游标卡尺读取并记录数据。根据所记录数据,将相邻峰谷的高度差视为谷深,相邻“峰-峰”或“谷-谷”的横向坐标之差视为波长。 遍历获取的各个截面的点都是静态数据点,利用弦测法对各个截面的数据进行谷深和波长的计算。以各纵向截面上所有点的Y坐标值的均值作为计算基准线,尽管纵向截面的轮廓在Z方向小尺度上会忽高忽低,在大尺度上却存在高于或低于基准线的“大波峰”与“大波谷”。基于此,忽略小尺度上波峰与波谷的影响,仅保留这些“大波峰”与“大波谷”的最值点,作为波长与谷深计算的基础。波长与谷深的计算流程如图4所示。 图4 波长与谷深计算流程 2.3.1 密度聚类算法 DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)是一种典型的密度聚类算法,该算法通过样本分布的紧密程度来假定样本的类别,将紧密相连的样本划为一类,就得到一个聚类类别[16,17]。DBSCAN算法的工作原理如图5所示,将数据点分为三类。 图5 DBSCAN算法的工作原理 核心点:在半径Eps内含有超过MinPts数目的点。边界点:在半径Eps的邻域内点的数量小于MinPts,但是落在核心点的邻域内。噪声点:既不是核心点也不是边界点的点。 2.3.2 谷深与波长的聚类分析 波磨可分为短波(波长30~80 mm)的波纹磨耗和长波(波长>80 mm)的波浪磨耗,其对应的波谷深度允许限值分别是0.3 mm和1.5 mm[18]。高速铁路对行车平稳性要求较高,短波的波谷深度允许限值也提高至0.2 mm[19]。波磨发生时会产生一定范围的接触斑[3,20],使得波长之间、谷深之间存在相似性,采用DBSCAN算法分别对波长和谷深进行聚类,可将相似或相同接触斑的数据尽可能地聚类在一块,经数理统计方法,即可得到对应钢轨的波磨信息。 DBSCAN使用的是全局的密度阈值MinPts和邻域搜索半径EPs,较大的EPs可将不同的波长聚类出来,但无法将较小的谷深聚类出来。反之较小的EPs可将谷深进行聚类,但可能引起波长聚类的数目太多影响效率且不精确,无法通过单一的EPs完成两个维度(波长与谷深)的密度聚类。对谷深聚类时要保证对0.1 mm以下的变化敏感,可令EPs=0.02 mm。至于波长聚类,要对10 mm的变化敏感,EPs=5 mm,聚类的具体流程见图6。 图6 波长与谷深聚类流程 为检验上述的邻域搜索半径EPs和密度阈值MinPts能否满足聚类要求,设计顶面廓形如图7所示的样件,在实验室条件下验证算法的可用性。 图7 样件纵向截面(单位:mm) 样件聚类计算结果与理论值对比见表1。表中k代表聚类成分,tv、cv表示理论值和计算值,h、l表示谷深和波长。 表1 样件聚类的理论与计算对比结果 mm 由表1可知,计算分析得到的短波共有4类,各类的谷深数值与理论相符,其偏差基本都在0.05 mm内,所取EPs与MinPts能满足聚类要求。 为验证上述算法的鲁棒性,设计a、b、c、d 4种顶面廓形不同的样件,对各样件进行10次重复性试验取计算均值,结果如表2所示。表中k代表聚类成分,tv、cv表示理论值和计算值,h、l表示谷深和波长。 从表2可以看出,该方法应对不同的样件时,表现良好,能够有效地分析出样件表面的形貌信息,鲁棒性较高。 为检验该算法的计算精度,在极限谷深和波长下,采用控制变量法对算法结果与理论值的偏差进行分析。首先,将样件设计成纵向截面的谷深分别是0.2,0.5,0.8 mm,波长分别为30,55,80 mm的连续正弦波,利用该方法对样件分别进行10次计算,结果如表3所示,表中h、l分别表示计算谷深和波长,ht和lt分别表示理论谷深和波长。 表3 短波范围内算法计算结果 由表3得,短波范围内算法的谷深计算绝对误差约0.025 mm,其相对误差随谷深的增大而减小,计算精度能满足实际检测需要[18]。为验证长波范围内算法的计算精度,将样件纵向截面设计成谷深分别是1.5,2,3 mm,波长分别是500,750,1 000 mm的连续正弦波,计算结果如表4所示,表中h、l分别表示计算谷深和波长,ht和lt分别表示理论谷深和波长。 表4 长波范围内算法计算结果 由表4可得,长波范围内算法的谷深计算误差在0.1 mm内,计算精度满足检测的要求[18]。 3.3.1 试验环境 在成都铁路局工务大机段进行了现场试验,试验对象为发生短波波形磨耗的站线。首先使用D&F160612型数显钢轨波磨仪对相应60 kg/m钢轨进行手工测量,如图8(a)所示,检测长度0.9 m,分辨率0.01 mm。然后,利用道岔结构光检测系统对同一段钢轨进行数据采集,如图8(b)所示。单次扫描幅面为400 mm×300 mm,单幅测量精度为0.03 mm,扫描点距为0.25 mm。 图8 现场试验 3.3.2 试验结果 该波形磨耗利用波磨仪测得的52个数据点如图9(a)所示,可以看出该钢轨发生了两种不同的波形磨耗,分别是谷深0.75 mm波长40 mm和谷深0.44 mm波长36 mm的波形磨耗。利用本文方法计算分析得到相应的两种波形磨耗:谷深0.81 mm波长39.5 mm、谷深0.485 mm波长37.4 mm的波形磨耗,并得到最大谷深发生在第14个截面处,即距钢轨中心面11.2 mm,将该截面数据输出如图9(b)所示。 图9 波磨仪与本研究方法测得的波形磨耗数据 3.3.3 精度与效率分析 手工检测与结构光检测结果对比如表5所示。 由表5可知,现场实测结果的谷深绝对误差在0.05 mm左右,相对误差在10%内。结构光系统采集的单幅钢轨点云Z坐标跨幅为350 mm,短波及波长为80~350 mm的波磨可一次拍摄完成检测;对于波长350~700 mm的波磨需拍摄两幅,点云需拼接两次,两幅点云的拼接误差约0.05 mm;对于波长700~1 000 mm的波磨需拍摄3幅,点云需拼接3次,3幅点云的拼接误差约0.10 mm。 表5 结构光检测与波磨仪检测偏差对比 由样件试验可知,短波范围内算法的谷深计算误差在0.025 mm内,扫描仪的检测精度为0.03 mm,本研究方法的短波谷深精度约0.055 mm,相对误差随谷深的增加而减小,现场实测结果与该规律相符合。长波范围内,算法的谷深计算绝对误差在0.1 mm内,相对误差为6.7%,因此长波范围内的计算精度基本能满足检测要求。 现场试验表明,波磨仪检测参数单一,结构光检测系统一次扫描可得到钢轨的垂磨、侧磨、肥边及波磨等多个参数,且随着检测长度增加,手工检测耗时费力的弊端逐渐突显,结构光检测系统的效率高于波磨仪。 (1)将三维结构光、弦测法和密度聚类算法结合起来对钢轨波磨进行检测,可有效地对不同谷深和波长进行分类计算,从而得到钢轨波磨的相关信息。 (2)实验室样件试验和现场试验表明,本研究方法测量短波波磨时的谷深精度约0.05 mm,满足波磨检测精度要求。相比波磨仪检测效率更高,适合长时间测量。同时,最大谷深所在的截面数据,能较好地呈现钢轨表面纵向的起伏变化情况,符合实际情况,本研究方法比惯性法更能反映钢轨实际轮廓表面。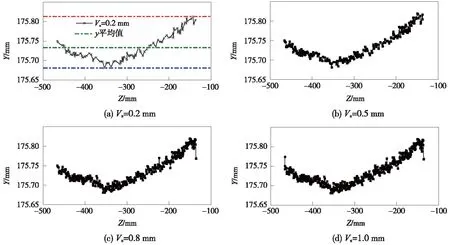
2.2 基于弦测法求取谷深和波长
2.3 密度聚类分析
3 实验室与现场试验
3.1 纵向平面遍历

3.2 可重复性试验
3.3 现场试验

4 结语
