面向站立姿态的操纵舒适性评价模型研究

赵 川，余隋怀，陈 晨，寸文哲，王 龙

(陕西省工业设计工程实验室(西北工业大学)，西安 710021)

站立姿态下手部的操纵舒适性是人机工效主要的评价内容之一.良好的操纵舒适性不仅减少操作人员疲劳，提高动作协调性和灵活性，而且影响生产效率和产品质量[1].目前，国内外针对操纵舒适性进行了大量研究，发现操纵人员的年龄、性别、操纵位置及操纵力等因素是影响上肢疲劳及肌肉负荷的重要因素[2-4]，而且采用固定站立操作姿势的工作人员肌肉骨骼损伤检出率高于采用坐姿操作的人员[5].

理想情况下设计师应该了解用户不同操纵位置相对应的舒适性，提高产品的设计质量.对于舒适性评价主要有两类方式：主观和客观评价[6].主观评价主要是获取被试者的心理感受，结果受被试者影响较大[7].客观评价是指借助相关标准、设备和评价方法对心理或生理参数进行测量[6].

虽然NASA[8]和Society of Automotive Engineers(SAE)[9]提供的标准非常全面，但是规定的可达域和舒适操作范围比较宽泛，在工程应用中有一定局限性[10].表面肌电图技术(sEMG)和脑电图(EEG)等能够精确获取被试者的数据，但通常受场景和经费限制[11-12].随着数字人体模型(Digital human models,DHMs)越来越多地应用于工程领域，良好的舒适性预测模型也是该类工具的主要期望功能之一.因此，将主观舒适度问题量化之后再进行数学建模，形成一套客观有效的舒适度评价方法具有重要意义.

文献[13]通过上肢关节力矩的动态变化值和上肢主要肌力变化量来分析舒适性，但是只考虑了三个关节角度，而且没有验证模型的精确性.Kolich M等[14]利用压力特征量和人体测量学量建立了舒适度评价的多元线性回归模型和神经网络预测模型.Kee[15]基于主观舒适性提出了3D iso-comfort舒适性曲面，通过关节角度建立回归模型分析主观舒适性，可以对桌面控制装置进行评价，但是只考虑了三个关节角度(肩部、肘部、手部)，因此不能对多自由度的姿势进行分析.基于数据驱动的评价方法被大量提出.沈阳[16]等采用线性回归方法，建立了微商车在四种路况(如：沥青、水泥、砂石和颠簸)下的不舒适度预测模型.文献[17]通过实验，收集被试者操纵姿势、目标位置、人体尺寸和主观舒适性数据，并利用实验数据建立舒适性预测模型.类似方法也被应用于汽车内饰评价和坐姿操纵舒适性评价[18-19].

由于人体姿势、运动控制以及主观评价的高变异性，通过实验方法研究操纵舒适性预测模型是非常有效的方法，但是目前对于站立姿势下的舒适性评价研究较少.T-S模糊神经网络(Takagi-Sugeno Fuzzy Neural Network，T-S FNN)作为一种将模糊逻辑与神经网络有机结合的系统，具有较强的容错能力和自适应学习性能，被广泛应用于处理各种不确定性和模糊性问题[20]，恰好符合主观舒适性预测问题不确定性、模糊性的需求.鉴于此，本文针对站立姿态下，基于T-S模糊神经网络建立手部操纵舒适性评价模型，该模型输入参数为操纵目标位置、关节角度、人体尺寸及脚部压力数据，输出参数为舒适性得分.

1 站立操纵作业研究对象

用户在站立姿态下操纵产品过程中涉及用户本身、产品和操纵环境，三者共同构成典型人机系统.在作业过程中，人的感知包含了对自身感知(即本体感觉)、触觉、视觉、听觉以及其他方面的知觉，多种知觉共同形成综合感知特征决定着舒适性.

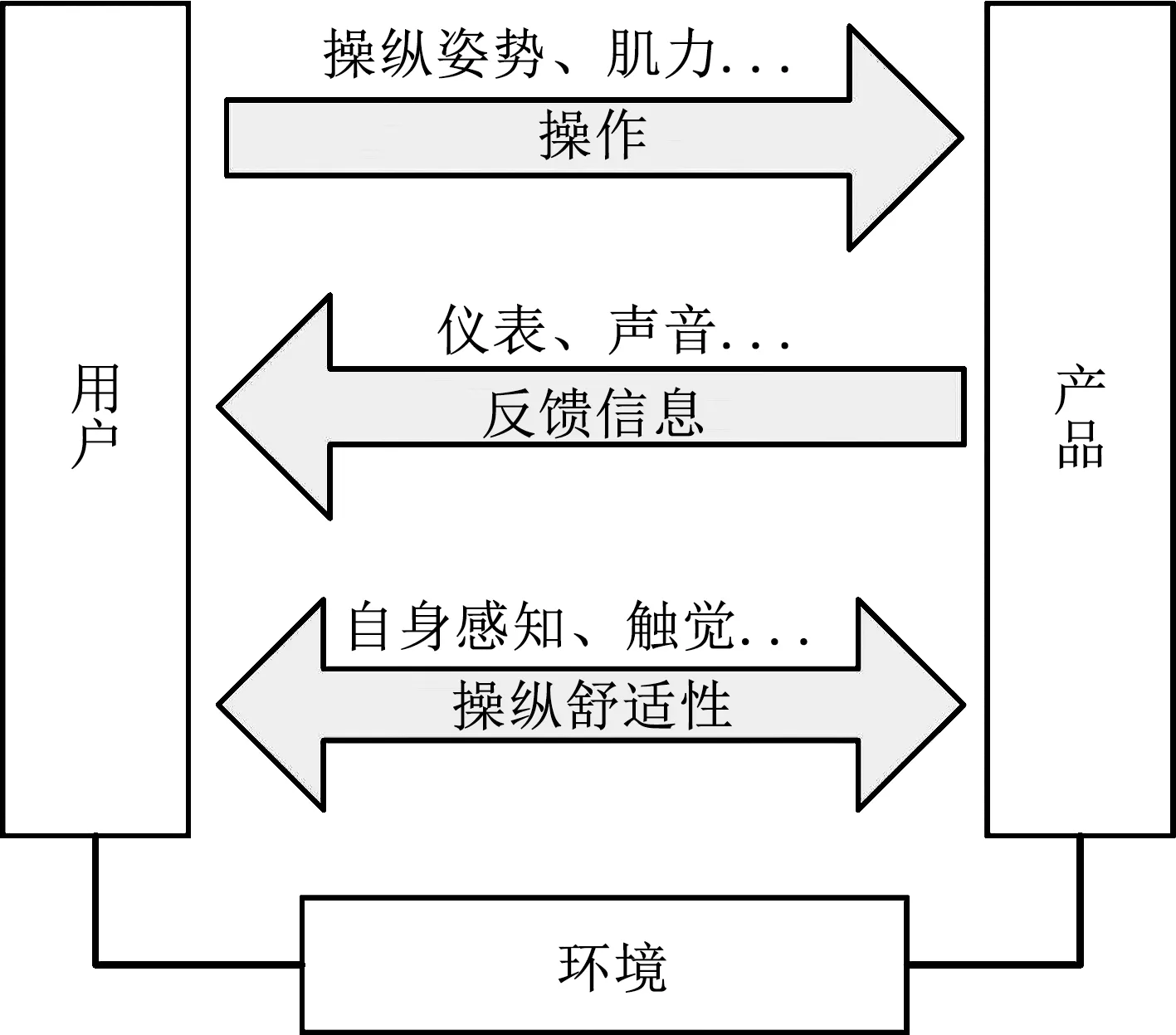
图1 人机关系示意

人要改变机器的运行状态，需要通过手或脚施加力于产品的操纵装置，对于操纵作业而言，其主要形式是操纵力，而操纵姿势直接关系到操纵力[21].机器对于用户具有反馈作用，主要通过仪表显示变化以及警报装置的声音提示等方式，引起人相应的感知，使用户能够了解产品的实时运行状态，以便完成作业任务.此外，人和产品都处在一定作业环境中，作业空间、照度、温湿度、振动条件以及特殊气体等因素都会对人的感受与产品的运行产生影响，如图1所示.在操纵过程中，由于操纵目的和产品运行状态在不断变化，故上述过程形成持续运行的闭环反馈模型.本研究主要对模型中产品位置及操纵姿势变化引起的感知变化进行预测.

2 操纵舒适性实验

根据上述分析，建立操纵舒适性分析评价模型首先需要获取与舒适性相关的用户、产品及操纵环境等数据.20名右手利者参与了本次实验，其中女性11名、男性9名.根据《中国成年人体尺寸GT 10000-88》，男性身高所占百分位数为50%～95%，女性身高所占百分位数为40%～99%，身体测量数据见表1.

为了分析不同操纵位置对用户舒适性的影响，25个圆形贴纸用来代表不同的操控位置.圆形贴纸的直径为3 cm，5行、5列均匀排列于塑料板上，每个圆形贴纸之间的间距均为20 cm.被试者要求自然站立，向前伸出右臂，上臂与躯干为90°，肘关节与肩部保持水平.调整塑标板位置使中指指尖触碰到第3行、第3列圆形贴纸的中心，此位置为被试者最大操纵范围为B3.在此基础上，增加塑料板水平距离10 cm为B4；减少水平距离15 cm为B2；减少水平距离30 cm为B1，如图2所示.目标中心位置根据每个被试者肩高和肩部到中指指尖的长度来决定.

表1 被试者人体测量数据

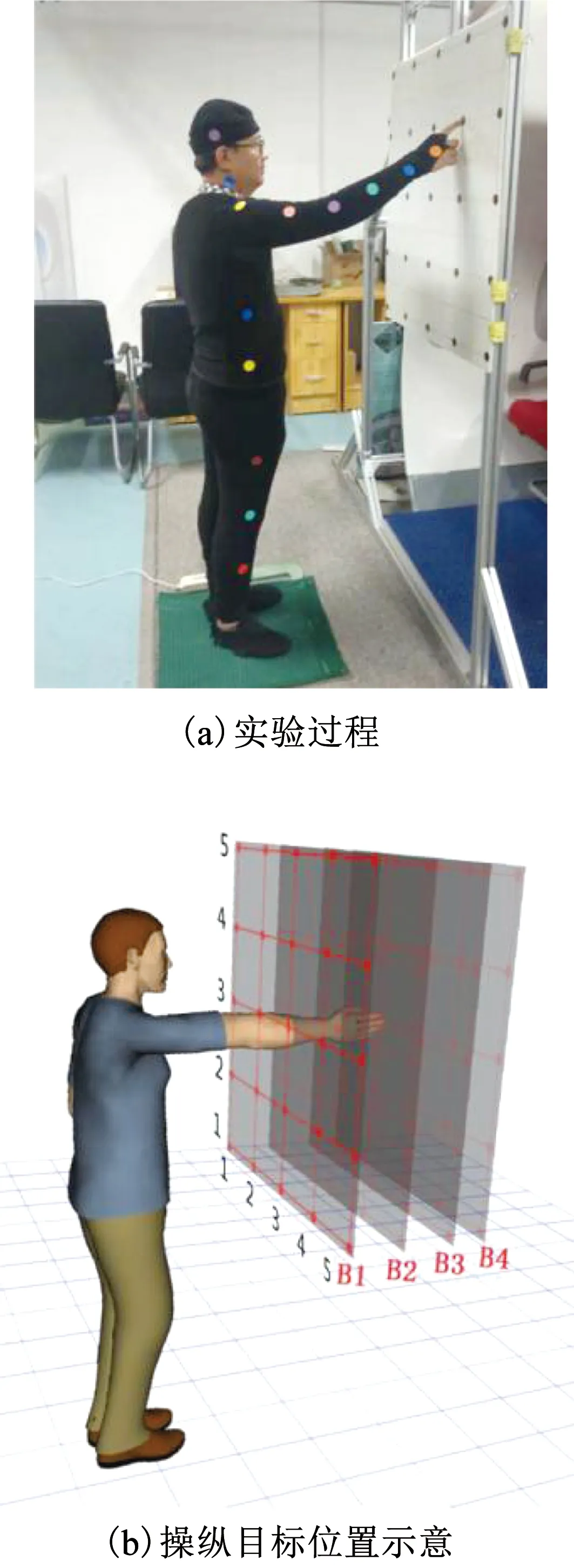
图2 操纵舒适性实验

实验开始后，被试者根据实验员的指示，用食指点击圆形贴纸中心，并保持5 s.点击过程中被试者可以自由弯腰、调整肩部和肘部来完成操作.但是不能调整站立位置和目标位置.塑料板和圆形贴纸的点击顺序都是随机决定，首先随机决定塑料板位置，然后随机决定要点击圆形贴纸的位置.一个点击任务完成后被试者需要休息1～2分钟，然后进行下次点击实验.被试者一共需要完成100次操纵任务(5行×5列×4个塑料板位置).

每次点击实验结束后，被试者要求完成CP-50(10)主观不舒适性问卷调查[22].问卷从0分～5分，分成6个类别，分别表示极端不舒适、非常不舒适、不舒适、中等、舒适和非常舒适.每个类别又细分成10个得分，得分低于10表示极端不舒适.实验开始前被试者需要熟悉该问卷.

实验过程中将不同颜色的贴片放置于被试者右侧的主要关节部位(颈部、肩部、上臂、下臂、手腕、腰部和腿部).利用1台SONY摄像机(HDR-CX510)进行拍摄，将摄像机放置在被试者右侧，观测角度与矢状面垂直，拍摄被试者整个身体的运动姿势.将视频数据导入Tracker (4.11.0，Open Source Physics)获取关节角度运动轨迹[23]，根据夹角计算公式获取关节角度，如图3所示.

采用压力座垫(Body Pressure Measurement System，Tekscan)，不间断地记录脚部体压分布.压力座垫包含1 024(32×32)个传感器，厚度为1.78 mm，测力范围从0 mmHg到250 mmHg(5PSI).压力座垫检测面积为471 mm×471 mm.在实际测量过程中，体压分布的平均压力(Mean pressure)和峰值压力(Maximum pressure)可以用来解释76.2%的体压分布数据变化，平均压力梯度(Mean gradient)和峰值压力梯度(Maximum gradient)，与被试者主观舒适性具有显著相关性[24-26].因此，本研究选择平均压力、峰值压力、平均压力梯度和峰值压力梯度4个体压分布参数对主观舒适性进行预测.

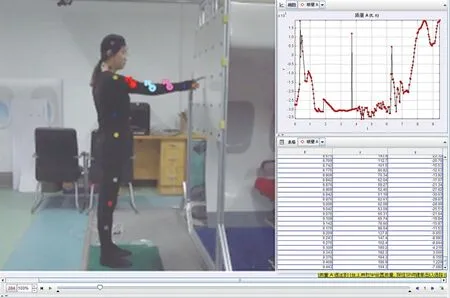
图3 关节角度计算

3 数据处理及操纵舒适性模型建立

实验结束后可以得到预测模型相应输入数据和输出数据.输入数据包括被试者身体测量数据、关节角度和操纵目标位置、压力座垫数据，输出为主观舒适性得分.

然而在实验过程中，由于问卷的主观不确定性，不同被试者对主观舒适性的判断也不同，所以在相同操纵位置舒适性得分也会有较大差异.而T-S FNN网络结构和参数需要根据样本的差异而自行调整，需要有较好的自适应能力.针对上述问题考虑到预测模型的结构辨识复杂、模糊规则选取较困难等弊端，本研究将箱式图(box-plot)引入到数据样本预处理中[27].针对不同被试者和操纵位置的舒适性得分差异，确定相应参数初始值，对样本数据进行筛选.有利于提高T-S FNN的效率和精确性，并增强网络的自适应性.

如图4所示.异常值(outlier)为偏离总体数据的数值，会对模型产生不可靠影响.IQR为上、下4分位之差，主要用以测量数据的离散程度，其中包含了50%的数据.上、下4分位(upper/lower quartile，Q3/Q1)，为第75%位数和25%位数.内上限(upper fence)为Q3+1.5*IQR，内下限(lower fence)为Q1-1.5*IQR.内上限和内下限以外的值为异常值.利用SPSS对主观舒适性数据进行异常值处理，结果表明共有异常值22个，剩余1 978个数据将用来训练舒适度评价模型.

该模型使用T-S FNN模糊推理系统，具备两组可训练参数.依据实验数据，可确定T-S FNN各层节点数和隶属度函数的参数初始值，如图5所示.有4类共21个输入，其中身体数据包括：性别、身高、体重、立姿举高、侧面手臂长、肩部指尖长、坐高和坐姿下肢长.关节角度包括：颈部、躯干、上臂、下臂、手腕和膝盖的角度.压力座垫数据包括：平均压力、峰值压力、平均压力梯度和峰值压力梯度.操纵目标位置：塑料板位置和圆形贴纸坐标X轴、Y轴坐标.每个输入有2个隶属度函数.该模型利用了典型T-SFNN结构，输出端每个端点都具有识别函数，根据训练数据设定阈值.给定训练网络的输入输出样本对后，建立T-S FNN模糊推理系统过程如下：

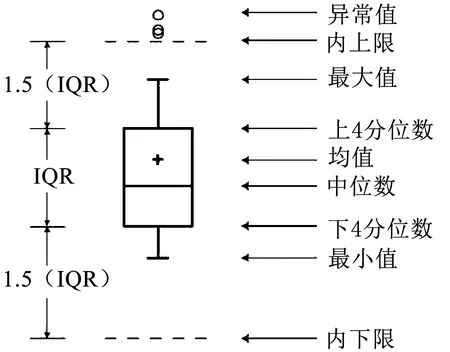
图4 箱型

第1层：第1层节点的数量(N)为每个输入自变量的数量(m=21)及相应隶属度函数(n=2).输出节点被定义为

Oij=μi,j(Xi),fori=1,m,j=1,n.

(1)

式中：μij为第jth个隶属度函数，采用高斯函数作为隶属度函数，Xi定义为

(2)

式中：a，b，c，为高斯函数的预定参数.

第2层：该层输出代表每个规则的强度.由输入层决定

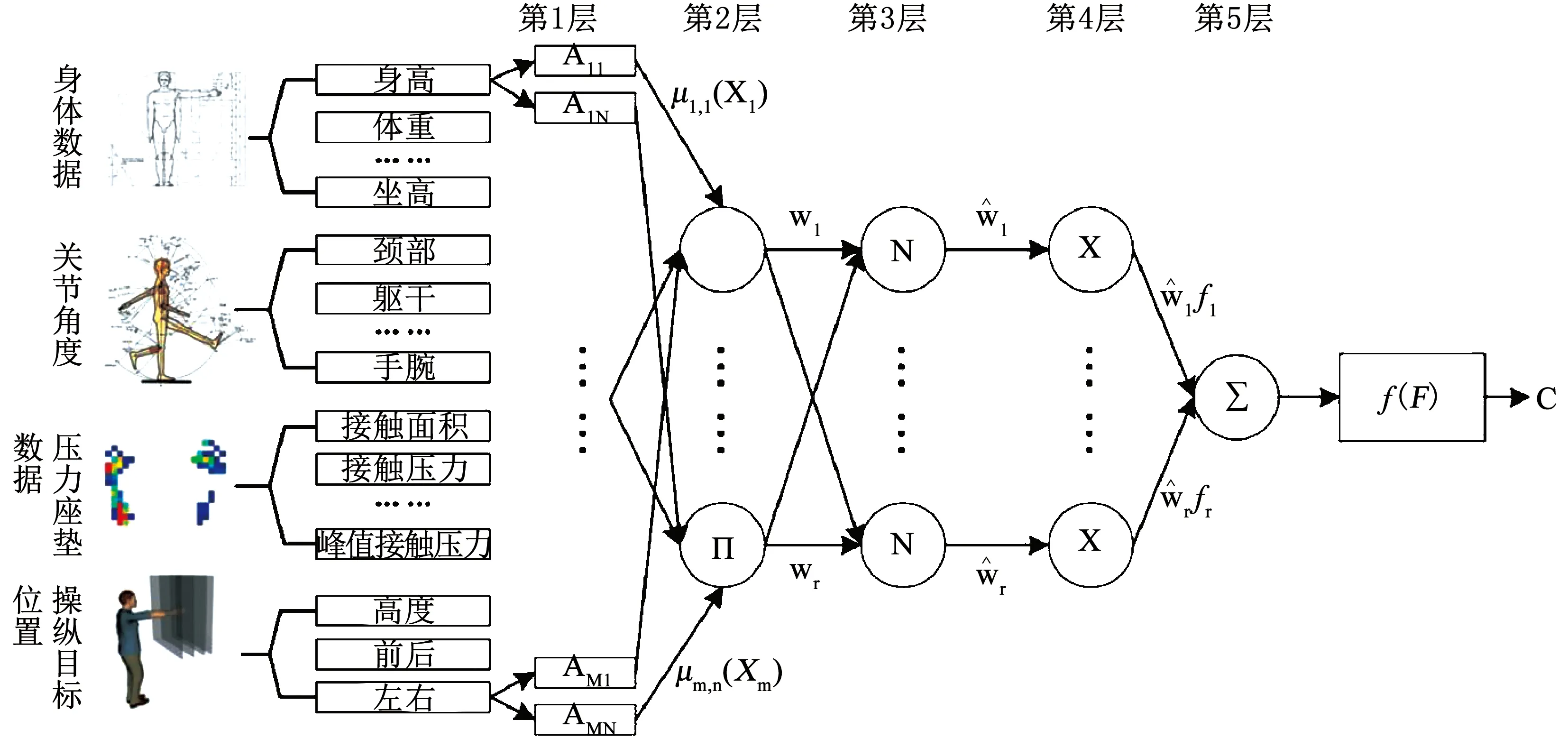
图5 操纵舒适性预测T-S FNN模型

Ok=Wk=μ1,i(X1)μ2,i(X21)…μm,i(Xm).

(3)

第3层：该层将输入节点k的权重进行无量纲处理

(4)

第4层该层输出为if-then规则的加权值：

(5)

式中:fk为第Kth个模糊规则

(6)

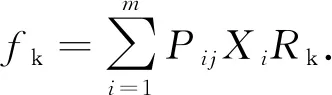
式中：Pij和Rk为后件参数，i=1；mj=1；nk=1；r.

第5层：该单节点层根据前4层的权重计算ANFIS最终结果(F)

(7)

最终，判别函数f(F)根据F的数值输出主观舒适性得分c.

90%(1780条)的实验数据用来对模型进行训练，10%(198条)的实验数据用来验证模型.T-S FNN的实现及计算过程通过Matlab(2016a)实现，如图6所示为操纵目标X轴和Y轴坐标位置对主观舒适度影响.在模型训练过程中使用反向传播算法与最小二乘法的混合方法，使该模型的前件参数和后件参数在训练过程中都经过了优化.

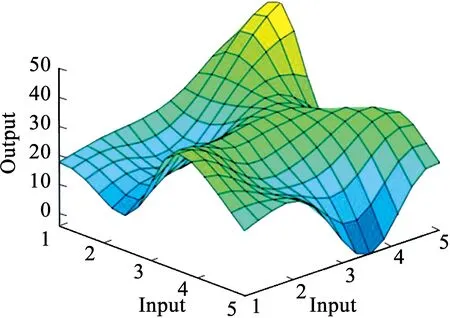
图6 目标位置对舒适性得分影响

最后通过对比该模型的预测舒适性值和实际舒适性得分均方根误差(REMS)验证该模型的有效性.RMSE用来表示实际值Cact和预测值Cest差别

(8)

式中：s为被试者数据索引，m=1,2,…,198,N为样本数量，N=198.

4 实例分析及性能验证

针对剩余10%(198条)实验数据，利用建立的T-S FNN预测模型获取被试者的操纵舒适性参数.如图7所示.为了说明T-S FNN预测模型的精确性，将该方法与BP神经网络的求解方法进行比较.通过Matlab，在相同运行环境、软件平台及实验数据下，设定BP神经网络的最大迭代次数Epochs=10 000，网络训练误差 ET=10-7.对操纵舒适性数据进行预测，如图7所示.由式(8)计算两种方法的预测值和实际值的差别，结果显示T-S FNN预测结果的均方根误差为1.53，BP神经网络预测结果的均方差为4.99，因此T-S FNN预测模型能够更好地反应被试者的真实情况.

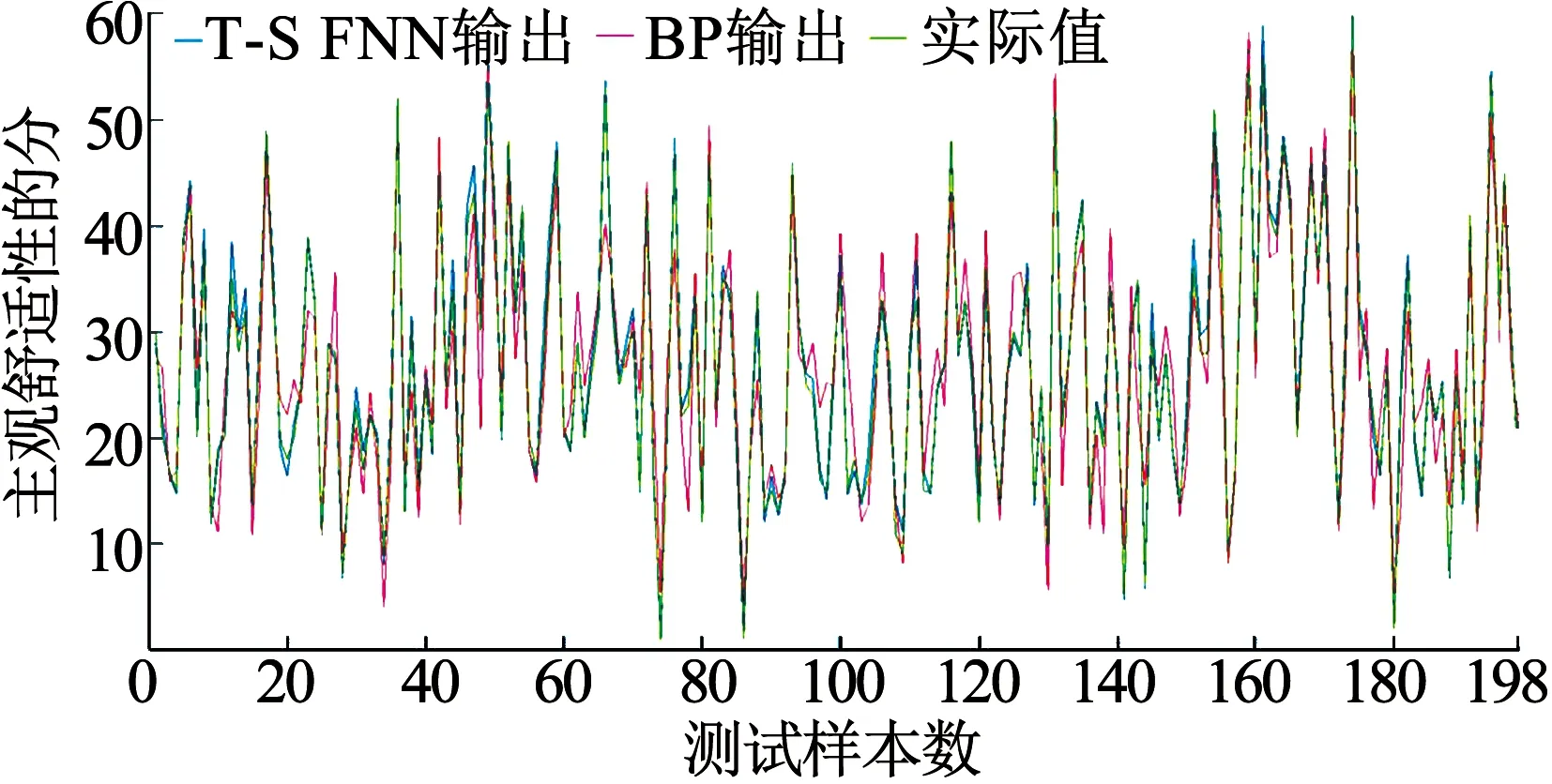
图7 模型预测得分

为进一步分析T-S FNN预测模型的有效性，随机选取了15组不同操纵任务，利用西门子人机工程仿真软件JACK[28,29]将被试者的关节角度作为输入计算相应的RULA[30]和OWAS[31]的评估结果.并采用Spearman等级相关，验证相关性，见表2.结果表明T-S FN的预测值与实际值相关性系数r=0.962，与RULA得分相关性系数r=0.833，与OWAS得分相关性系数r=0.694，通过查询《Spearman秩相关系数临界值表》[32]，当样本数n=15，相关性系数r>0.654时，我们有99%的置信度认为两个随机变量相关.所以在P=0.01的置信水平上来看，T-S FN的预测值不仅和实际值是等级相关，而且与RULA和OWAS的评估结果显著相关.

表2 Spearman 相关性分析

5 结论

本文在数据驱动的方法基础上提出一种基于T-S FNN的站立姿态操纵舒适性预测模型.通过站立操纵实验收集主观舒适性得分、目标位置、关节角度、人体尺寸及脚部压力数据.针对主观舒适性得分差异，通过箱式图对样本数据进行筛选，提高了T-S FNN的预测效率和精确性，最后构建了针对站立姿态的T-S FNN舒适性预测模型，从而实现对站立姿态下不同操纵位置的主观舒适性预测.与BP神经网络预测模型进行比较，也可看出T-S FNN模型可以对样本精确学习，具有较强泛化能力，并且预测精度高.最后随机选取15组不同操纵任务，采用Spearman等级相关，验证了T-S FN的预测值不仅和实际值有显著相关性，而且与RULA和OWAS的评价结果显著相关.以该方法为基础，可以进一步构建各影响因素与操纵舒适性指数的映射模型，并将其导入数字人体模型中，对站立姿态下的操纵舒适性进行预测，可有效地减少工作中上肢疲劳及肌肉负荷问题.但是，由于被试样本量较少、年龄众分布较集中等因素，使得大量历史数据信息需要不定时维护与更新，以不断提高预测结果对实际操纵舒适性动态变化的适应性，下一步将结合手臂和肩部的肌电数据展开更深入研究.