粒组尺寸缺陷对颗粒破碎极限分形维数的影响

雷练武, 于钱米， 李金钊, 曹玉鹏, 牛吉强, 陈岁芳

(1.宁波华东核工业工程勘察院,浙江 宁波 315040;2.山东科技大学 交通学院,山东 青岛 266590;3.潍坊学院 建筑工程学院,山东 潍坊 261061)

分形理论可以透过无序混乱现象和不规则形态，揭示隐藏在复杂现象背后的规律、局部和整体之间的本质联系，该理论已经广泛用于解决地质和岩土工程中复杂问题(谢焱石等, 2008；胡青华等, 2011；钱琨等, 2017；王艳艳等, 2019；张晓峰等，2016)。关于不同初始级配粗粒土颗粒破碎极限分形维数的研究很多(徐永福, 2017；张季如等, 2015, 2016)。其中部分研究是对侧限条件下的粗集料施加静压力或冲击荷载，分析有限作用次数下的颗粒破碎结果直接得到有限荷载条件下的分形维数，另一部分研究是利用有限荷载条件下颗粒破碎过程中相关数据进行建模，预测出极限情况下的分形维数。这些方法耗费时间长，其破碎结果准确度受实验条件影响非常大。从另一个角度分析，粗集料堆积稳定之后，如果内部颗粒面与面接触，单向受力作用很难使粗集料内部颗粒破碎。颗粒间存在的孔隙为颗粒发生破碎和破碎过程中颗粒空间移动这两种行为提供了更多可能性，实际粗集料中颗粒形状不规则、不均匀，堆积稳定后颗粒间存在孔隙是必然的。颗粒破碎过程可被理解为破碎产生的新颗粒向多余孔隙移动的过程，该过程与粗集料初始堆积状态直接相关，因此从初始堆积状态的角度研究测量颗粒破碎极限分形维数的方法可节省时间和提高准确度。

还有研究利用对固定形状颗粒排列组合或分析颗粒破碎过程中颗粒尺寸变化规律等几何学方法计算颗粒破碎极限分形维数(赵中岩等, 1992；Stäger et al., 2018；Yu et al., 2019)。赵中岩等(1992)研究了碎裂岩的极限分形模型，模型中各子块尺寸取决于初始正方体边长，而且相邻子块间无缝隙，此限制使碎裂岩的极限级配具有了间断性。Yu等(2019)使用增长路径(GP)方法生成的粗集料破碎的二维极限分形模型保持了极限级配的连续性，因为第n条路径(PAn)不表示正方体的边长，而是代表第n个颗粒粒组的尺寸，它含粒径介于筛孔径dn和dn+1之间的所有颗粒。GP方法生成的极限Sierpinski垫片(Ettestad et al., 2018)的总面积取决于初始增长路径(GP0)或初始路径(PA0)的起始点d0(最大筛径)的数值大小。使用GP方法分析二维极限分形模型是一种理想的方式，给定任意一个d0(d0>0)，都可以使用GP方法得到与d0相对应且极限分形维数约等于2.585的结果。实际通过室内筛分试验得到某个粒组，只是因为筛分试验后该粒组处于孔径为dn和dn+1的两个筛子之间，并没有测量该粒组内所有颗粒粒径的实际分布情况。

综上所述，有必要研究新的、简单的室内实验方法。该方法能够快速测量初始状态基本参数，高效计算单一初始粒组粗集料的极限分形维数；基于新方法的测量结果，进一步深入研究初始粒组中粒径间断性对粗集料颗粒破碎极限结果的影响，这对深入分析和预测颗粒破碎规律具有指导意义。

1 极限分形维数新实验测量方法

1.1 计算原理

极限分形维数是由颗粒破碎极限百分比计算得到的。颗粒破碎极限百分比的实验测量原理如图1所示。图1显示的单一颗粒粒径粗集料初始堆积状态具有最大孔隙比(emax)。单向破碎模式1是指单一颗粒粒径粗集料中部分颗粒破碎后与没有破碎的颗粒一起重新排列而消除孔隙的过程。单向破碎模式1的破碎结果(y%)需要根据初始堆积状态的emax测量值进行计算。单向破碎模式2是指单一颗粒粒径粗集料中所有颗粒都发生破碎后重新排列消除孔隙的过程。单向破碎模式2的破碎结果(100%)是理论最大破碎值。实际破碎模式介于这两种单向破碎模式之间。

1.2 实验方法

本研究使用两种粗颗粒实验材料：石英砂和粗粒土，分别取自砂厂和共玉高速路基基床填料。石英砂(QS-1)包含4个粒组，颗粒粒径d分别为1.18～2.36 mm、0.425～1.180 mm、0.250～0.425 mm、0.075～0.250 mm，密度都是2.66 g/cm3。粗粒土(CS-2)包含4个粒组，颗粒粒径d分别为1～2 mm、0.5～1.0 mm、0.25～0.50 mm、0.075～0.250 mm，密度分别为2.61 g/cm3、2.70 g/cm3、2.64 g/cm3、2.63 g/cm3。粒组用PSF表示。

将6份不同体积的单一粒组石英砂通过漏斗慢速倒入6个同型号量筒内，用工具轻轻抹平量筒内粗集料表面，记录6个量筒内的体积(Vi,单位cm3，i=1～6)，测量过程中禁止震动，防止孔隙缩小，影响测量结果。使用电子秤测量并计算出与石英砂Vi对应的质量(Mi,单位g)。每一个关于Vi和Mi的数据都需要测量3次，最终结果取3次测量结果的平均值。

石英砂孔隙体积(Vi,void)计算公式为：

Vi,void=Vi-Mi/2.66

(1)

对于粗粒土而言，式(1)中Mi/2.66中的分母将随PSF的变化而变化。将石英砂破碎颗粒的最少质量设为Mx, 则：

(2)

石英砂最小破碎百分比(yi,单位%)计算公式如下：

(3)

石英砂极限平均破碎百分比(Pu,单位%)计算公式如下：

(4)

基于Vi和Mi的测量结果，石英砂和粗粒土不同粒组的yi(i=1～6)和Pu计算结果分别见表1和表2，其中PSFij中i=1时表示材料是石英砂，i=2时表示材料是粗粒土，j表示第j个粒组。

表1 石英砂的Pu测量结果

表2 粗粒土的Pu测量结果

当初始孔隙比固定，新生成的颗粒会向初始颗粒间的孔隙内移动，即新生成颗粒所占空间大小取决于初始颗粒之间的空间大小，据此原理可计算出极限平均破碎百分比(Pu)，某个粒组PSFi的极限平均破碎百分比用Pu,PSFi表示。Pu,PSFi是指极限破碎状态条件下小于粒组PSFi的所有新生成粒组的质量百分比，也是极限破碎状态条件下小于粒径di的所有新生成颗粒的质量百分比。因此小于等于某粒径的质量百分比(P≤di,i=1, 2, …, 5)的计算公式见式(5)～(9)。石英砂和粗粒土的P≤di计算结果如表3所示。

P≤d1= 100 (%)

(5)

P≤d2=Pu, PSF1×P≤d1(%)

(6)

P≤d3=Pu,PSF2×P≤d2(%)

(7)

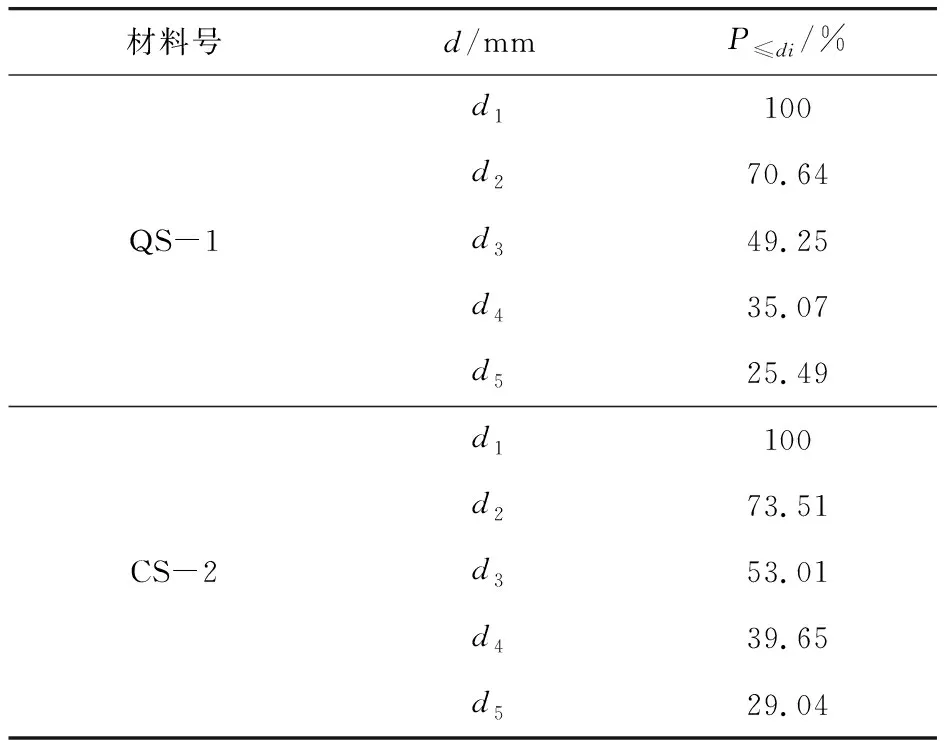
表3 两种材料的P≤di计算结果

P≤d4=Pu,PSF3×P≤d3(%)

(8)

P≤d5=Pu,PSF4×P≤d4(%)

(9)

式中，d表示QS-1的粒径时分别为：d1=2.36 mm、d2=1.18 mm、d3=0.425 mm、d4=0.25 mm、d5=0.07 mm；d表示CS-2的粒径时分别为：d1=2 mm、d2=1 mm、d3=0.5 mm、d4=0.25 mm、d5=0.075 mm。

1.3 结果分析

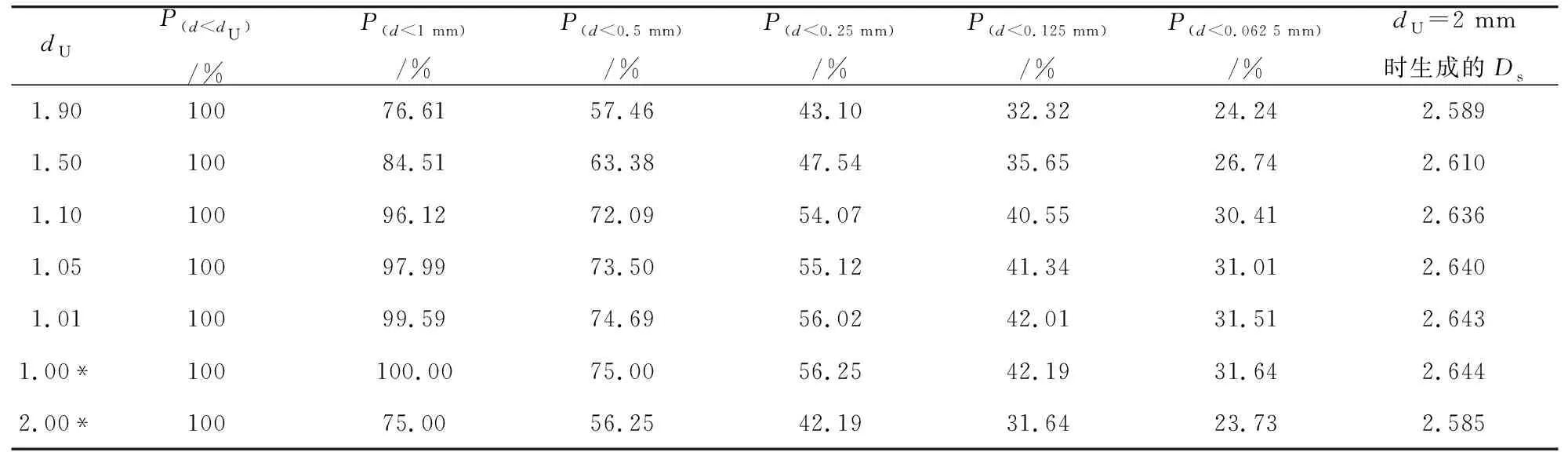
表4显示了通过双对数图拟合计算分形维数(Ds)的参数值(图2的横坐标和纵坐标数值)，基于表4的数据，图2分别给出石英砂和粗粒土的颗粒破碎极限Ds的计算步骤，极限Ds结果都约等于2.6，这与已有研究结果(徐永福, 2017；Yu et al.,2019)一致。如果要使极限Ds约等于2.6，极限Ds的变化范围应是2.55

表4 用于计算分形维数的参数值

2 初始粒组不完整尺寸对分形维数的影响

上述实验研究发现，两种颗粒材料的极限Ds都约等于2.6，如果极限Ds数据的小数点后位数不止保留1位，该数据是介于2.55和2.65之间。在研究分析了粗集料颗粒堆积初始孔隙率对极限破碎结果影响的基础上，进一步分析初始粒组不完整尺寸对极限破碎结果的影响。

2.1 符号解释

(1)d0是最大筛径，d0=2 mm；d1是二级筛径，d1=d0/2；d2是三级筛径，d2=d1/2；d3是四级筛径，d3=d2/2；d4是五级筛径，d4=d3/2；d5是六级筛径，d5=d4/2；di是粒组中的颗粒粒径。

(2)PSF0是初始粒组，尺寸是d0～d0/2；PSFn是第n个粒组(n=1,2,3,4,5)，尺寸是dn～dn/2。

(3)粒组尺寸大小的比较是通过粒组中粒径平均值的比较来体现，粒径平均值是粒组中最大粒径和最小粒径的平均值；本研究中假设粒组中粒径变化规律为线性平均分布。

(4)dL是初始粒组尺寸的下界值，即粒组中粒径的最小值，dU是初始粒组尺寸的上界值，即粒组中粒径的最大值。

2.2 实际PSF0的粒径变化范围是[dL,d0]

该情况指实际PSF0尺寸大于理论PSF0尺寸，即实际PSF0的平均粒径大于理论PSF0的平均粒径，d0/2

2.3 实际PSF0的粒径变化范围是[d0/2,dU]

该情况是指实际PSF0尺寸小于理论PSF0尺寸，即实际PSF0的平均粒径小于理论PSF0的平均粒径，d0/2≤dU

图4为把粒径介于dU和dU/2的PSF当作PSF0条件下dU=1.9、1.5和1.1的三个Ds=2.585的线性拟合图。三个线性拟合公式分别是式(10)、(11)和(12)：

y=0.415x+0.009 25

(10)

y=0.415x+0.051 85

(11)

y=0.415x+0.107 76

(12)

式中，y=lg[P(d

当x=-0.301 03 (di=1 mm时)，通过式(10)、(11)和(12)可以求得dU=1.9、1.5和1.1条件下的三个y值分别是-0.115 69、-0.073 09和-0.017 18，与之对应的三个P(d<1 mm)分别为76.61%、84.51%和96.12%。同理，其它P(d

当在实际筛分试验之后把dU和d0/2之间的PSF当作d0和d0/2之间的PSF进行处理求Ds时，把表5中的P(d

表5 6个dU条件下的P(d

3 结论

(1)研究出一种新实验方法，快速测量了粗集料颗粒堆积初始孔隙率，高效计算了单一初始粒组粗集料的极限分形维数约等于2.6。

(2)当实际初始粒组平均尺寸大于理论初始粒组平均尺寸时，颗粒破碎之后，会自动补充生成实际初始粒组缺少的尺寸颗粒。这种初始粒组尺寸缺陷对极限分形维数的计算不会造成误差。

(3)当实际初始粒组平均尺寸小于理论初始粒组平均尺寸时，颗粒破碎之后，不会自动补充生成实际初始粒组缺少的尺寸的颗粒。该初始粒组尺寸缺陷对极限分形维数的计算会造成误差。存在误差的极限分形维数与初始粒组的最大尺寸成对数关系。实际计算结果只保留小数点后1位，存在误差的极限分形维数都约等于2.6，该情况可忽略较小误差的存在。