一类具有优自相关性质的二元序列的2-adic复杂度研究
2020-02-21卢栎羽柯品惠
卢栎羽, 柯品惠
(福建省网络安全与密码技术重点实验室; 福建师范大学数学与信息学院, 福建福州 350117)
1 引言
线性反馈移位寄存器(LFSRs) 和带进位的反馈移位寄存器(FCSRs) 是两种伪随机序列发生器.它们所产生的序列具有良好的伪随机性质, 如低相关性、长周期等.这些伪随机序列在密码学和通信系统中有着广泛的应用.理论上, 任何二元周期序列都可以由LFSR或FCSR 生成.人们通常把能产生序列s的最短LFSRs (或FCSRs) 的长度称为序列s的线性复杂度(或2-adic 复杂度), 用符号LC(s)(或φ2(s)) 表示.而Berlekamp-Massey 算法(BMA)[1]和FCSRs 的有理逼近算法(RAA)[2]分别是针对序列的LFSRs 和FCSRs 的有效算法.如果序列的线性复杂度或2-adic 复杂度偏低, 则该序列在密码学意义下就是不安全的.因此, 线性复杂度和2-adic 复杂度被认为是序列的两个重要的安全准则.而对于流密码中的密钥流生成器产生的周期序列, 为了抵抗RAA 其2-adic 复杂度应不小于其周期的一半.
交织技术是分析和设计序列的重要技术之一.许多最优自相关序列[3,4]、低相关序列集[5,7]、或低相关区序列集[8]都是采用交织技术设计的或者被证明具有特殊的交织结构.例如, 利用交织结构, Tang 和Gong 在文献[3]中构造了三类具有优自相关性质的序列, 进一步地, Li 和Tang 在文献[9]证明了这些序列具有大的线性复杂度.Arasu 等在文献[10]中构造了一类具有最优自相关性质的序列, 进一步地, Wang 和Du 等在文献[11]中证明其具有大的线性复杂度.后来, Tang 和Ding 在文献[4]中给出了比文献[3]和[10]更一般的构造.上述所提到的交织序列基本都由两类不同的序列构成, 且它们的形式为或但是这类序列的2-adic 复杂度一直没人计算, 直到Xiong 等在文献[12]中提出一种利用循环矩阵去计算二元序列的2-adic 复杂度的方法, 以及Hu 在文献[13]中提出运用自相关值的精确分布去计算二元序列的2-adic 复杂度的方法.此外, 利用循环矩阵, Xiong 等在文献[12]中证明了所有具有理想自相关值的序列的2-adic 复杂度可达到其最大值.Xiong 等在文献[14]中证明了两类基于交织结构构造的序列也具有最大2-adic 复杂度.这两类序列中的一类是由Tang 和Ding 构造的[4], 该序列具有最佳自相关性质; 另一类由Zhou 等构造[15], 该序列的相关值可达到最优的Tang-Fan-Matsufuji 界.此外, 利用文献[13]提出的方法和精确自相关值分布, Sun 等在文献[16]和文献[17]中分别给出了两类序列的2-adic 复杂度的下界.
Tang 等[4]给出了一类具有优相关性质的二元序列的构造.最近, Yan 等[18]推广了文献[4]的构造, 并给出了该序列的自相关值的具体分布.本文将研究该序列的2-adic 复杂度.具体地, 本文将在Tang 和Yan 等构造的二元序列的基础上, 利用Hu 的方法, 给出这些序列的2-adic 复杂度的一个下界.全文安排如下: 第2 节给出了交织结构和勒让德序列的定义, 并回顾了Tang 和Yan 等给出的一类具有优相关性质的二元序列的构造及其性质; 第3 节, 给出了该二元序列的2-adic 复杂度的一个下界; 第4 节对本文工作做了小结.
2 预备知识
2.1 交织结构
设v是一个正整数,si=(si(0),si(1),···,si(v −1)),0≤i ≤u −1 为u个周期为v的二元序列.构造一个v×u矩阵I=(Ii,j) 如下
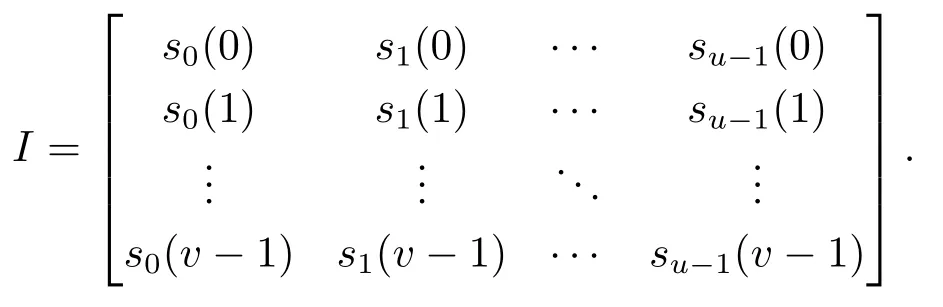
按行连接上述矩阵可得到一条长为uv的周期序列s, 称序列s为si, 0≤i ≤u −1 的交织序列, 记为s=I(s0,s1,···su−1), 其中I表示交织算子.
2.2 勒让德序列
设p是一个奇素数, 勒让德符号定义如下

其中QRp和NQRp分别为模p的二次剩余和非二次剩余.
勒让德序列定义如下
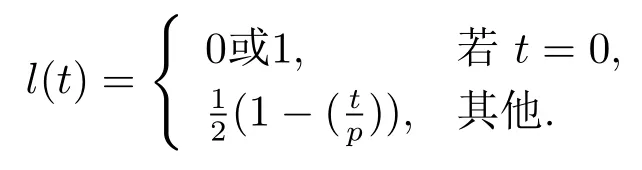
当l(0) = 1 时, 称l(t) 为第一类勒让德序列, 记作l(t); 当l(0) = 0 时, 称l(t) 为第二类勒让德序列, 记作l0(t).
设p是一个奇素数,a和b是周期为p的第一类或第二类勒让德序列, 定义二元序列s如下

其中Lη(a) 表示序列a左循环移η位,表示a的补序列.
引理1[18]设序列s定义如上, 则
(i) 当p ≡1 (mod 4), 且a=l(t),b=l0(t) 时, 序列s的自相关值分布如下

(ii) 当p ≡1 (mod 4), 且a=l0(t),b=l(t) 时, 序列s的自相关值分布如下

(iii) 当p ≡3 (mod 4), 且a=l(t),b=l0(t) 时, 序列s的自相关值分布如下

(iv) 当p ≡3 (mod 4), 且a=l0(t),b=l(t) 时, 序列s的自相关值分布如下

3 主要结论
设N是一个正整数, ZN为模N的剩余类环.设s= (s(0),s(1),···,s(N −1)) 为周期为N的二元序列, 定义其序列多项式为由文献 [19]可知, 若
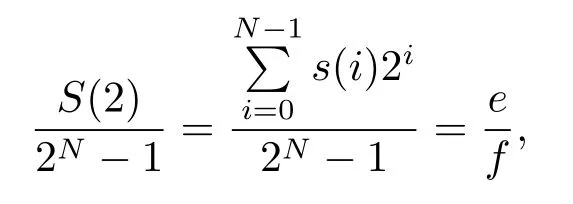
其中 0≤e ≤f,gcd(e,f)=1.则序列s的 2-adic 复杂度φ2(s)为其中z为小于或等于z的最大正整数.
引理 2[13]设s=(s(0),s(1),···,s(N −1)) 是一条周期为N的二元序列,S(x) 为s的序列多项式, 记则
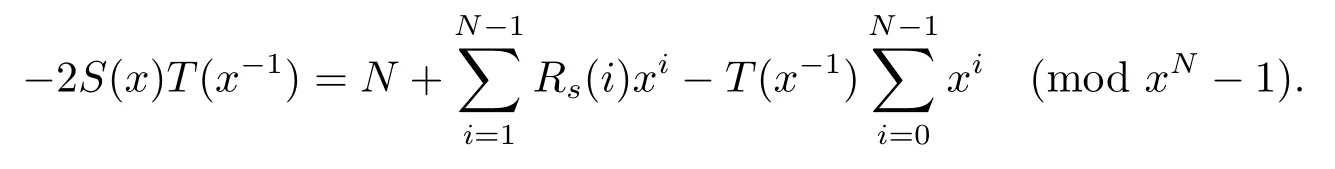
引理3设p为奇素数且p ≡1 (mod 4),s为式(2.1)定义的二元序列,其中a=l,b=l0,则有gcd(S(2),5)=1.
证由
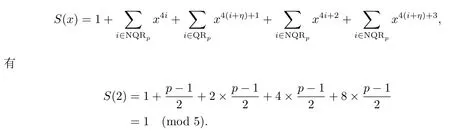
进而gcd(S(2),5)=1.
引理 4设p为奇素数, 则有
证(1) 由 22p ≡1 (mod 3) 及 22p ≡−1 (mod 5) 易知.
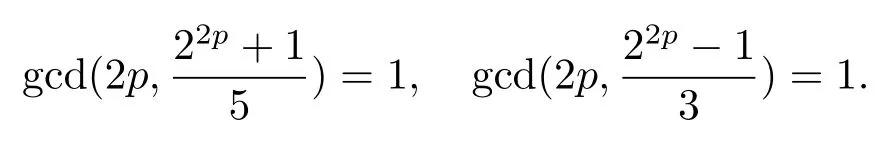
定理1设p为奇素数且p ≡1 (mod 4),s为式(2.1)定义的二元序列,其中a=l,b=l0,且则序列s的 2-adic 复杂度φ2(s) 满足φ2(s)≥2p, 即序列s的 2-adic 复杂度大于其周期的一半.
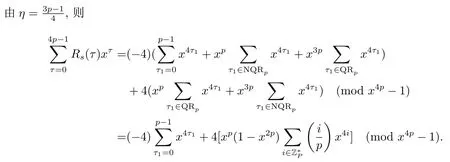
证设τ=4τ1+τ2, 其中 0≤τ1 由引理2, 有 由引理 3 及引理 4, 有 gcd(S(2),24p −1)≤22p −1.因此有由φ2(s) 的定义知结论成立. 推论1设p为奇素数且p ≡1 (mod 4),s为式(2.1)定义的二元序列,其中a=l0,b=l,且则序列s的 2-adic 复杂度φ2(s) 满足:φ2(s)≥2p, 即序列s的 2-adic 复杂度大于其周期的一半. 证注意到, 该序列和定理1 中序列很相似, 差别在于交织构造中的基序列略有差异.进而它们的2-adic 复杂度的分析类似, 但是具体的计算细节也略有差异.设τ=4τ1+τ2, 其中0≤τ1 由引理2, 有 类似定理 1 的证明, 由引理 3 及引理 4, 有 gcd(S(2),24p −1)≤22p −1.再由φ2(s) 的定义知结论成立. 引理5设p为奇素数且p ≡3 (mod 4),s为式(2.1)定义的二元序列,其中a=l,b=l0,其序列多项式为S(x), 则有gcd(S(2),3)=1. 证由 进而gcd(S(2),3)=1. 定理2设p为奇素数且p ≡3 (mod 4),s为式(2.1)定义的二元序列,其中a=l,b=l0,且则序列s的 2-adic 复杂度φ2(s) 满足φ2(s)≥2p, 即序列s的 2-adic 复杂度大于其周期的一半. 证设τ=4τ1+τ2, 其中 0≤τ1 由引理2, 有 再由φ2(s) 的定义, 有 因此结论成立. 推论2设p为奇素数且p ≡3 (mod 4),s为式(2.1)定义的二元序列,其中a=l0,b=l,且则序列s的 2-adic 复杂度φ2(s) 满足φ2(s)≥2p, 即序列s的 2-adic 复杂度大于其周期的一半. 证注意到, 该序列和定理2 中序列很相似, 差别在于交织构造中的基序列略有差异.进而它们的2-adic 复杂度的分析类似, 但是具体的计算细节也略有差异.设τ=4τ1+τ2, 其中0≤τ1 由引理2, 有 由引理4 及引理5, gcd(S(2),24p −1)≤22p+1.再由φ2(s) 的定义可知 本文研究了一类具有优自相关性质的二元序列的2-adic 复杂度, 给出了该类序列的2-adic 复杂度的一个下界.本文的结果表明这类序列的2-adic 复杂度不小于其周期的一半,这意味着这些序列可以抵抗针对带进位的反馈移位寄存器的有理逼近算法的攻击.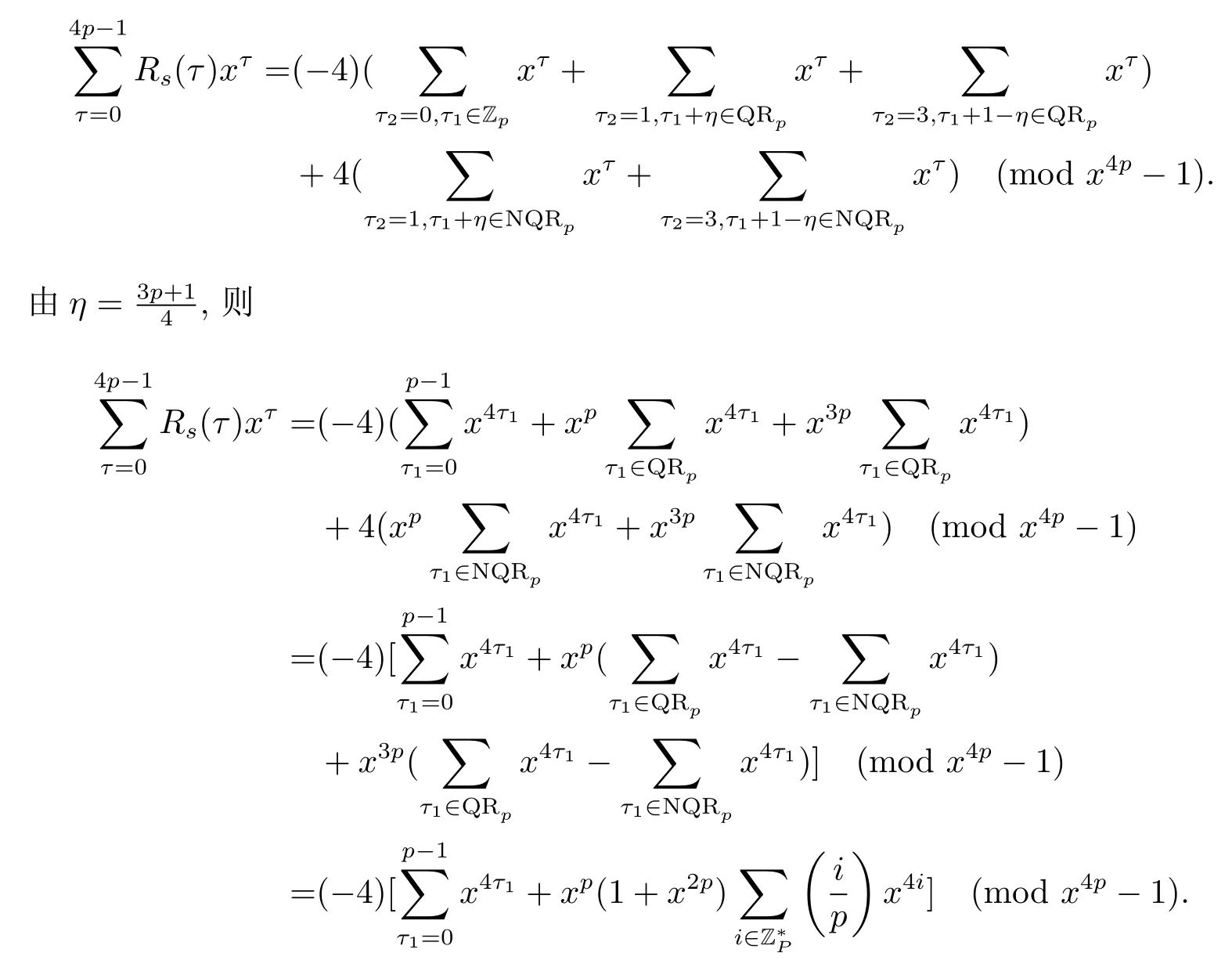
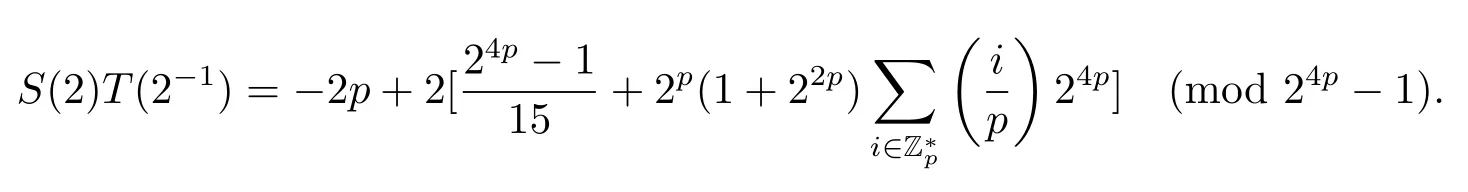
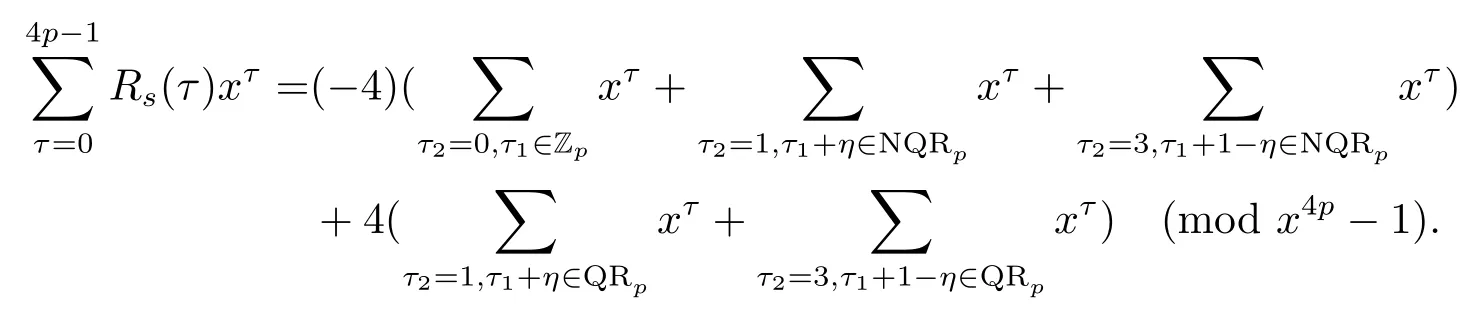
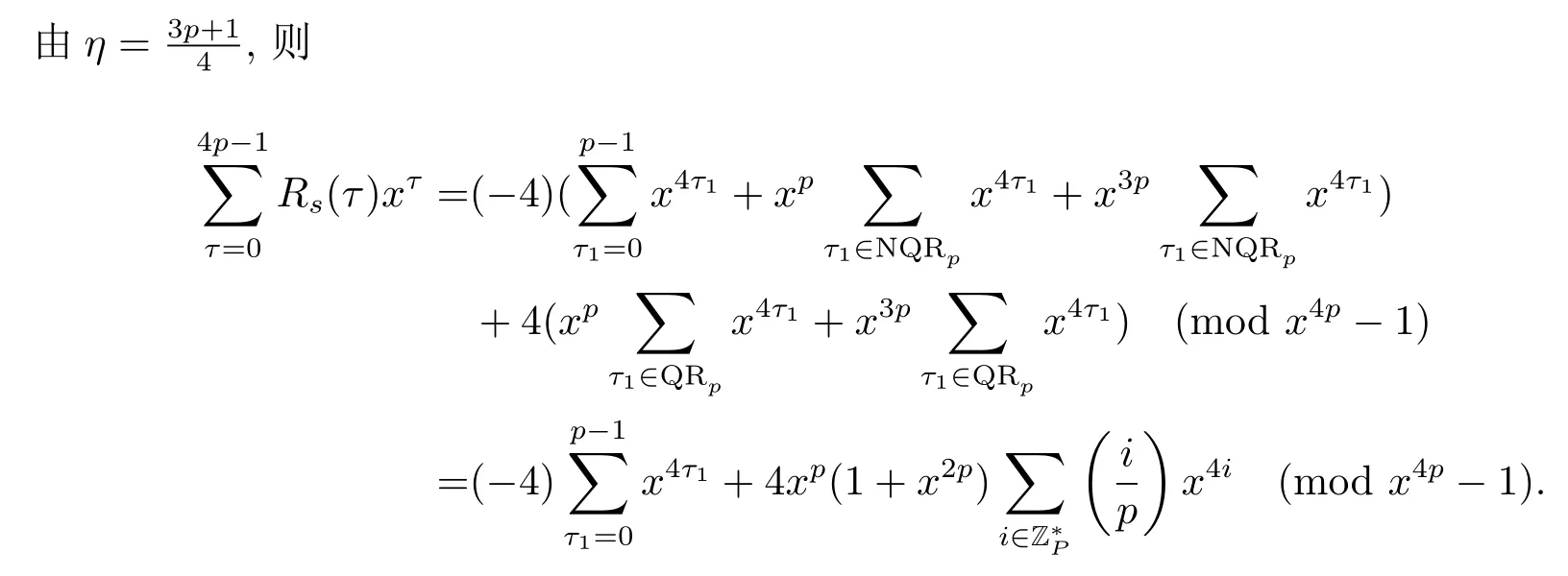
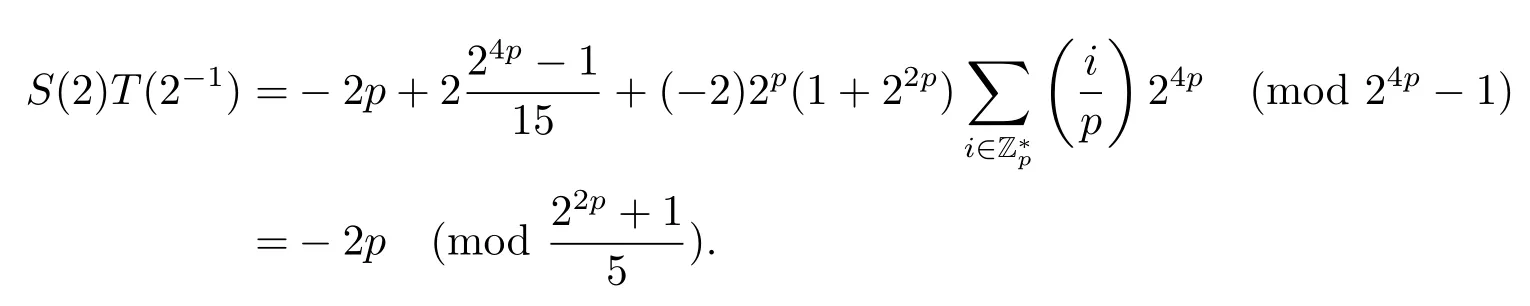
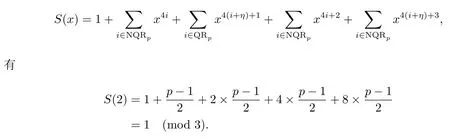
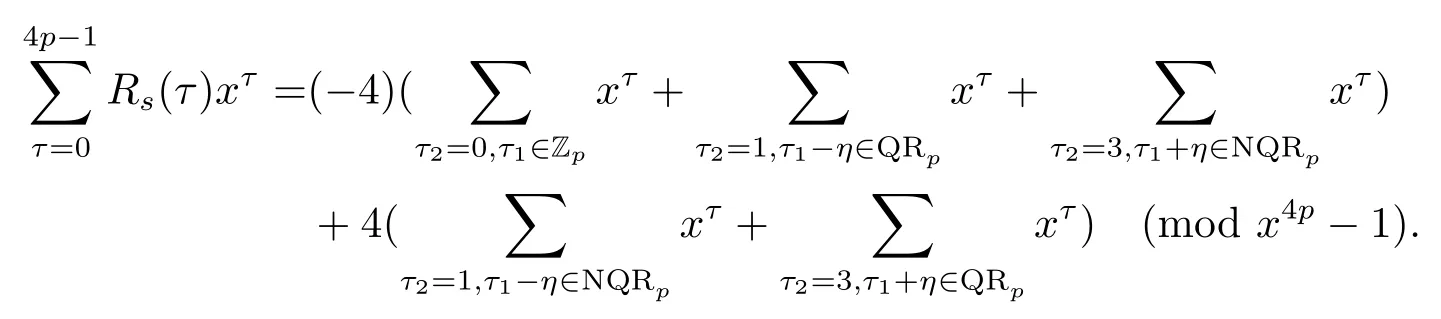

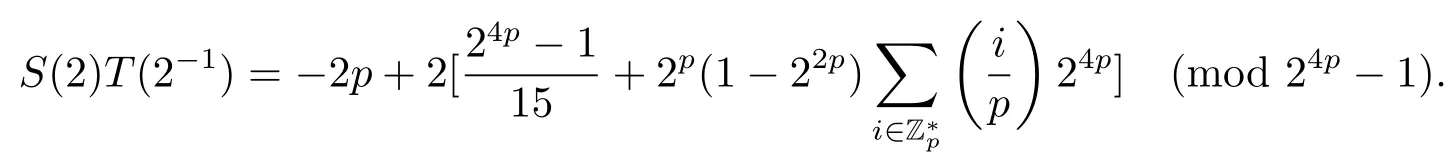
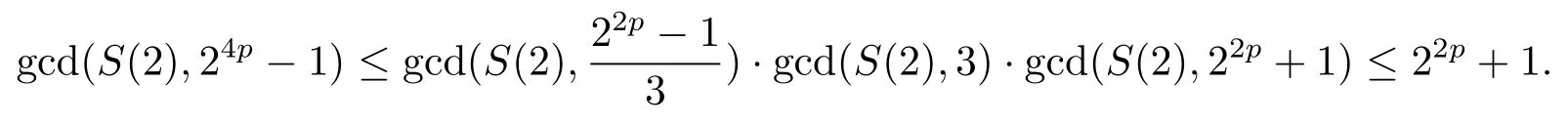
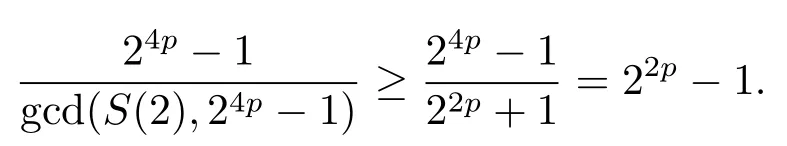
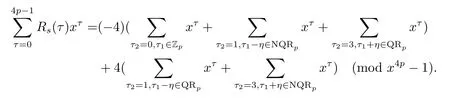
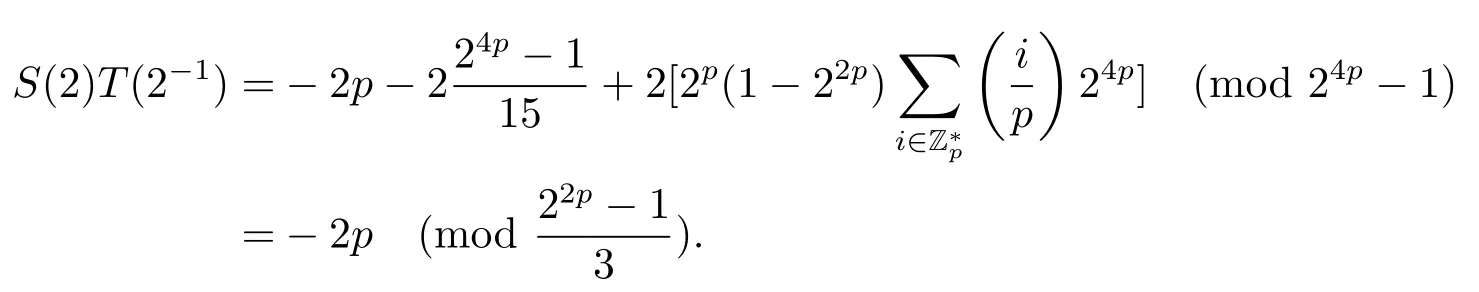
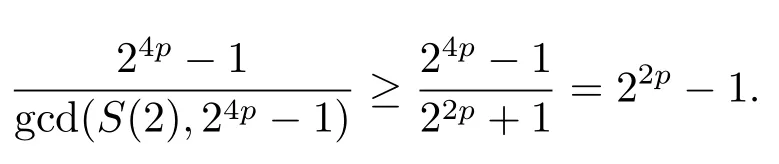
4 总结
猜你喜欢
杂志排行
数学杂志的其它文章
- LEONARD PAIRS CONSTRUCTED FROM THE QUANTUM ALGEBRA νq(sl2)
- BOUNDEDNESS OF THE FRACTIONAL INTEGRAL OPERATOR WITH ROUGH KERNEL AND ITS COMMUTATOR IN VANISHING GENERALIZED VARIABLE EXPONENT MORREY SPACES ON UNBOUNDED SETS
- IMPROVE INEQUALITIES OF ARITHMETIC-HARMONIC MEAN
- A CLASS OF NON-MATCHABLE DISTRIBUTIVE LATTICES
- SHARP ESTIMATES FOR EIGENVALUES OF BI-DRIFTING LAPLACIAN
- 素的∗-代数上的非线性混合Lie三重ξ-导子
