多普勒测风激光雷达三波束反演方法与实验❋

宋小全， 王芳涵， 尹嘉萍， 王希涛， 刘晓英， 任文核， 吴松华

(1. 中国海洋大学信息科学与工程学院海洋技术系，山东 青岛 266100； 2.青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室，山东 青岛 266237； 3.青岛镭测创芯科技有限公司，山东 青岛 266101)

随着能源危机的严峻，世界各国日益重视新能源的开发与利用。风能储量丰富，分布广泛，是最有竞争力的可再生清洁能源之一[1]。风场特征测量是发展风电行业的基础性工作，传统的测风手段是风电测风塔，其建设成本较高、周期长、无法移动，为风场测量带来很多不便。激光雷达测风是当前较为成熟的一种遥感测风技术，激光雷达体积小、重量轻、安置移动方便，目前已经被国内外风电相关机构广泛应用[2]。近年来，国内外学者研究发现，商业化测风激光雷达的观测数据质量与超声风速计、风廓线雷达相当[3-10]。2017年3月，IEC接纳测风激光雷达作为风场信息测量装置为风电场进行风功率曲线测试和风资源评估[11]，推动了激光雷达在风电行业的应用。

多普勒测风激光雷达从工作原理上分为相干探测和非相干探测两种。与非相干探测相比，相干探测精度高、信噪比高、易于集成、应用领域更广。目前多普勒测风激光雷达的风场和风廓线波束扫描反演方法主要有VAD(Velocity Azimuth Display)[12]，VVP(Volume Velocity Processing)[13]，RHI(Range Height Indicator)[14]，DBS(Doppler Beam Swinging)[15]等。

DBS方法与其他反演方法相比，需要的波束更少，能够在更短时间内完成，适用于气流不稳定的情况[15]。传统的DBS方法是用五波束方法(DBS-5)反演风廓线，需要东、西、南、北、垂直五个方向的径向数据[8]。三波束方法(DBS-3)可利用满足条件的三个方向径向数据反演出风廓线信息，测量时间更短，理论上可提高数据刷新率和获取率，能够在气流不稳定的情况下捕捉到更多风场特征。本文基于青岛镭测创芯科技有限公司Wind3D 6000型多普勒测风激光雷达系统及实测数据，利用三波束方法将标准产品level 0径向风速数据进行重新计算和反演，并与由激光雷达内置五波束方法反演得到的标准产品level 2平均风廓线数据进行水平风速、风向等风场特征参数的比对和分析，取得了一致效果。

1 基本原理

多普勒测风激光雷达利用光的多普勒效应来实现。激光雷达向大气中发射激光光束，光束在大气中传播时会受到大气中气溶胶等粒子对激光的散射作用，当气溶胶等粒子相对于激光雷达有运动时(通常气溶胶的整体移动速度即等效视为风速)，望远镜接收到的散射回波信号光与本振光在光电探测元件表面拍频，得到一个差频信号，即多普勒频移。通过公式(1)可由多普勒频移反演出气溶胶运动在激光束方向上的分量，即径向速度或径向风速：

(1)

式中：fD为多普勒频移；Vlos为径向速度；V为气溶胶相对激光雷达的运动速度；λ为发射激光的波长；γ为风向与激光光束的夹角。

五波束方法扫描模式如图1(a)所示，该方法利用东西南北四个方向的径向数据反演水平风场，垂直风速由垂直方向的波束直接测得，可用于复杂地形的风速校正，计算公式如下所示：

(2)

式中:u为北向南风速分量；v为东向西风速分量；VE、VW、VS、VN和VZ分别为东西南北和垂直方向上的径向风速；θ为激光光束与水平面的夹角；Vh为水平风速；w为垂直风速。

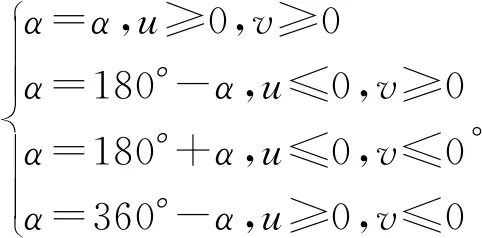
(3)

三波束方法可利用相互正交的两个方向加垂直方向共三个方向的径向数据进行反演，如图1(b)所示，理论上缩短了观测时间，可提高数据刷新率和获取率，仅用五波束方法约五分之三的时间即可反演出风廓线结果，计算公式如下：

(4)

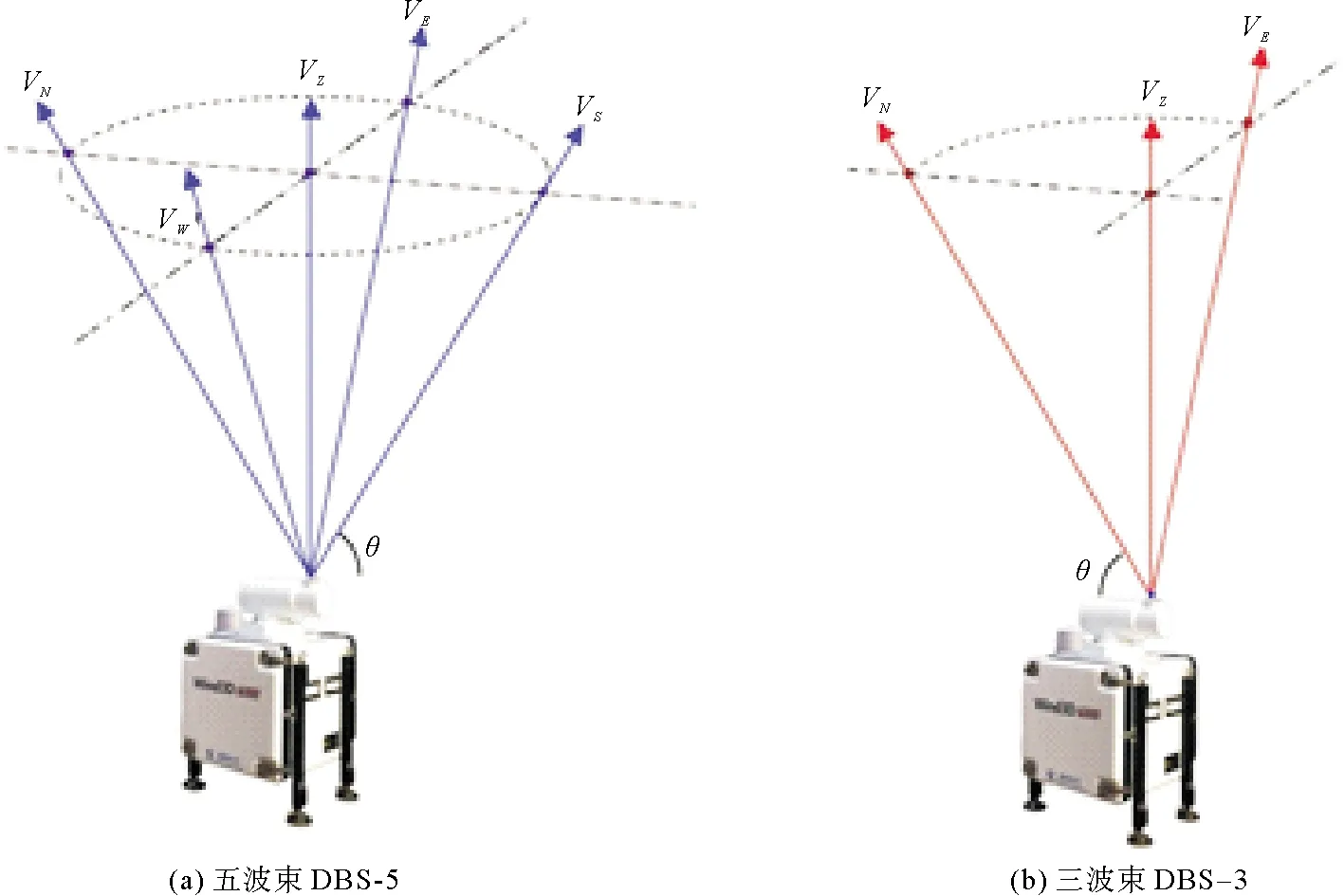
图1 扫描原理图

2 实验概况

2.1 实验地点

实验场地位于中国海洋大学崂山校区信息南楼西侧，实验场景如图2所示。实验观测时间自2018年7月4～16日，共13 d。

2.2 实验仪器

本研究使用的观测设备为青岛镭测创芯科技有限公司提供测试的Wind3D 6000型测风激光雷达，是一种小型三维扫描型系统，测量45～6 000 m高度范围的风速、风向廓线，输出秒级、平均风廓线数据，可用于风资源评估、功率预测的风廓线测量[16]，具体技术参数如表1所示。

图2 激光雷达测量现场

激光雷达标准数据产品包括level 0径向风速数据、level 1秒级风廓线数据、level 2平均风廓线数据等。level 0径向数据是某波束的径向风速数据，即风速在测量波束方向的速度分量；level 1秒级数据由系统内置的标准五波束方法实时计算得到；level 2数据的平均时间可在测量前设置，根据GB/T 18451.2—2003中对测风数据的要求[17]，本次实验设置的平均时间为10 min。

表1 激光雷达技术参数

3 数据处理及分析

3.1 数据处理及质量控制

三波束方法利用激光雷达的level 0径向数据中的垂直波束与两个相互正交的波束进行计算，我们随机选取了北、东、垂直三个方向，计算方法见公式(4)。

在实际观测中，激光雷达探测的信号包含有用回波信号和噪声信号，激光雷达所测量的原始数据的精度主要受设备噪声的影响，取决于回波信号和噪声的比值，即信噪比(Signal Noise Ratio, SNR)，信噪比是一个十分重要的性能指标，反映了系统探测能力的强弱。

在对原始回波信号进行处理时，首先对傅里叶变换谱数据进行平均，以去除背景噪声、提高信噪比；同时利用声光调制器将中频信号的频率提高，去掉相对强度噪声。但此时信号光中的散粒噪声仍会对风速反演造成影响，因此在数据处理时需要对低信噪比引起的失真风速信号进行去除。文章利用设定信噪比门限阈值的方法进行质量控制，计算前先对北、东、垂直三个方向的信噪比SNRN、SNRE、SNRZ进行判断，若高于信噪比门限阈值则进行计算，否则将其视为无效信号，不参与计算和分析[13]。

设置信噪比门限阈值可能会剔除一部分无效信号，如果无效信号太多，可能会导致该时段有效数据过少、该组数据不具代表性。为避免此类情况，对秒级数据进行10 min平均处理时，设定一个数据有效率门限阈值进行数据质量控制。数据有效率定义为质量控制后有效数据点数占该时间段内数据总点数的比值，可由公式(5)得到。

(5)

式中：κ为该时间段内的数据有效率；Nvalid为该时间段内有效数据点数；Ntotal为该时间段内数据总点数。当10 min内数据有效率大于该门限阈值时，对其进行平均处理，否则将该时间段的数据视为无效数据，不进行比对分析。

数据质量控制的流程如图3所示。文章综合考虑对观测数据精度和数据完整率的影响，设定了信噪比门限阈值、数据有效率门限阈值两个判据来减小原始数据噪声的影响。为期13 d的测量期间，以90 m高度上共取得1 781组10 min平均数据为例，经质量控制后得到1 752组有效数据，数据有效率为98.37%，满足使用需求。数据无效或缺失可能是由降雨、气溶胶或极端天气引起[3]。

对秒级数据进行平均处理时，风速平均采用算术平均法，风向平均采用矢量平均法，能够很好地解决风向变化跨零的问题，是目前最准确的风向平均方法[18]。

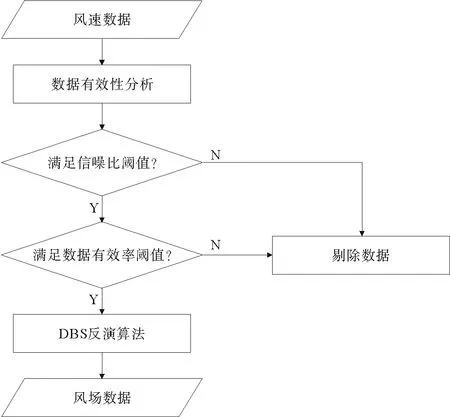
图3 质量控制流程图

3.2 数据分析

针对风资源评估与风功率曲线印证常见的风机高度与叶轮直径，文章主要选取90 m高度的测量数据进行分析和比对。

3.2.1 时间序列分析 图4为90 m高度风速和风向的时间序列图，为期13 d的测量共获取1 752组有效比对数据点对，红线表示用三波束方法的计算结果，蓝线表示激光雷达内置五波束方法的计算结果。可以看出，两种方法反演得到的风速和风向在变化趋势和数值大小上始终保持较好的一致性。

3.2.2 相关性分析 为了更好的比对两种方法在不同湍流条件下的处理结果异同，在做相关性分析时同时计算和考虑了湍流强度。湍流强度表征指定周期内水平风速的变化情况，可由公式(6)[19]得到。

(6)

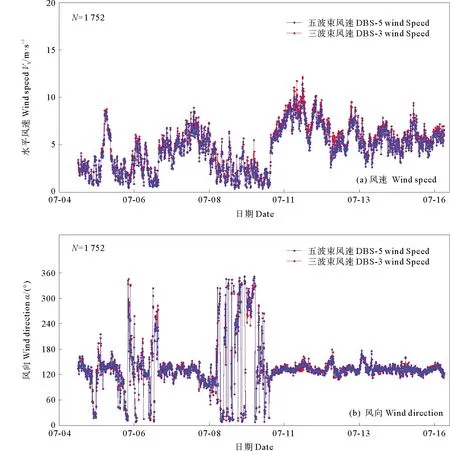
图4 90 m高度时间序列分析

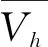
图5为90 m高度两种方法计算结果的相关性分析，数据点的不同颜色表示湍流强度的不同大小。图5(a)为风速值的相关性分析，可以看出，数据点集中在1∶1线附近，用最小二乘法求得的线性回归方程的斜率为1.037 3决定系数为0.982 5，平均偏移量bias为0.28 m·s-1，平均偏移量为正表示三波束方法计算得到的风速值较系统标准产品数值偏大。图6为90 m高度处不同湍流强度下风速的相关性分析，总体来看，湍流强度越大，数据点越偏离1∶1线，即两种方法之间的差异越大。表2为不同湍流强度下两种方法计算得到的风速的相关性分析，可以看出，随着湍流强度的增大，相关系数有减小趋势，平均偏移量的绝对值有增大趋势。

图5(b)为风向值的相关性分析，为消除风向跨零情况对数据分析的影响，根据IEC标准，在0°两侧分别剔除7.5°的数据，仅保留[7.5°，352.5°]扇区内的数据[11]，剔除扇区后有效比对数据点对为1 717组。可以看出线性回归方程的斜率为0.988 1，决定系数为0.976 9，平均偏移量为0.38°，平均偏移量为正表示三波束计算得到的风向值较系统标准产品数值偏大。从图中可以看出，风向一致性与湍流强度的关系与风速类似，湍流强度增大，两种方法之间的差异呈现增大趋势。

表3为77、90和181 m三个高度上风速值的相关性分析，可以看出三组数据都集中在1∶1线附近，决定系数均在0.98以上。

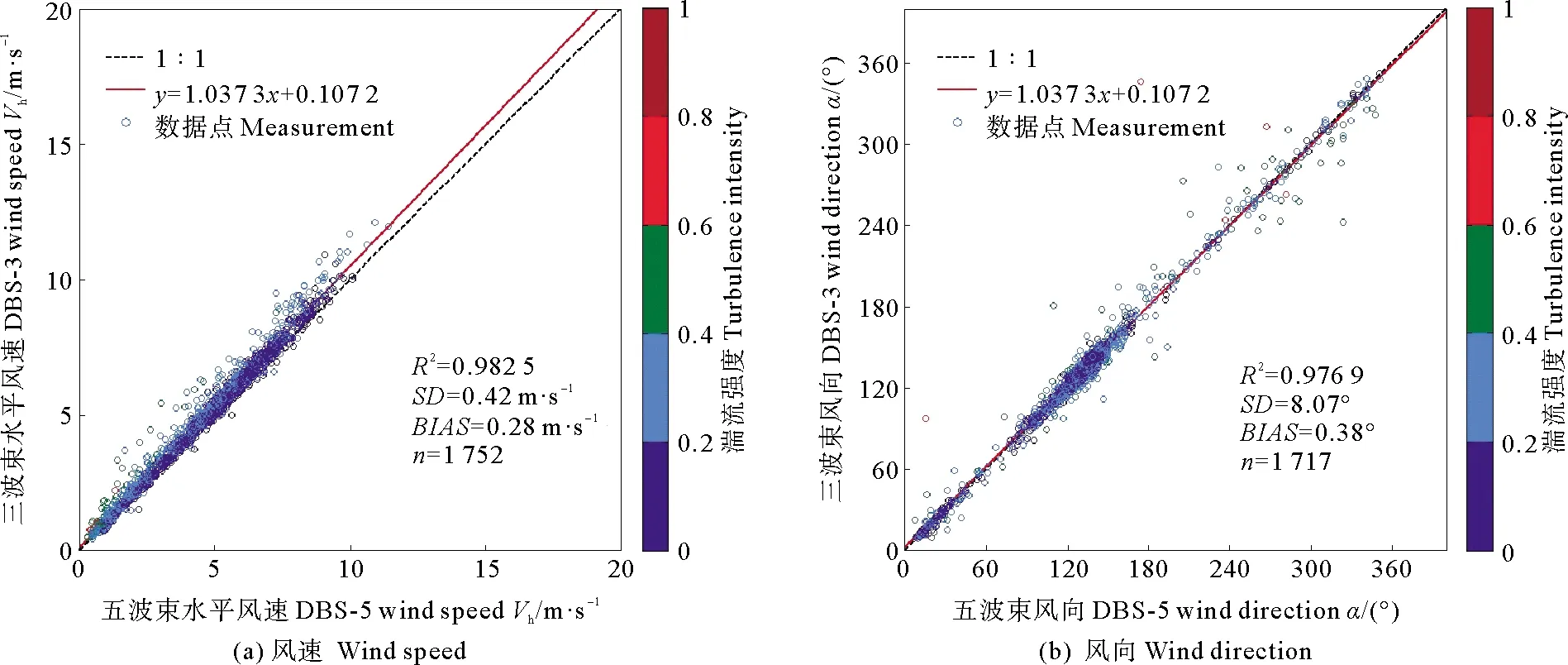
图5 90 m高度相关性分析

图6 90 m高度处不同湍流强度下的风速相关性分析

3.2.3 区间平均值分析 为了研究风速大小对两种方法测量结果的影响，本研究对实验数据进行了区间平均值的分析。根据IEC标准[11]，将风速分为1 m·s-1的风速区间，每个区间中心值为1 m·s-1的整数倍，若风速区间内数据点数小于6时不进行统计分析。

图7表示90 m高度每个风速区间内三波束方法和五波束方法反演结果平均偏差的比对分析。图7(a)表示每个风速区间内风速差的平均值分布情况，误差棒表示三波束计算结果在该区间内的标准偏差，绿色折线表示风速在每个区间的分布情况。可以看出，风速数量统计符合威布尔分布，两者风速差的平均值均在0～1 m·s-1范围内，风速差为正表示三波束方法反演的风速较大。随着风速的增大，两者差异有逐渐增大的趋势，两种风廓线反演方法在存在差异的原因及各风速段哪种方法更准确有待进一步观测和研究。图7(b)表示每个风速区间内风向差的平均值分布情况，为减弱风向跨零对标准差的影响，当两者风向差大于270°或小于-270°时，分别对其进行减或加360°。可以看出，随风速增大，风向差的平均值和标准偏差均有减小趋势。风向差平均值最大为21.96°，其标准偏差为14.19°，所在区间为0.5～1.5 m·s-1，这可能是由于风速过小导致，根据IEC标准，风速小于4 m·s-1的数据可不做比对和分析。

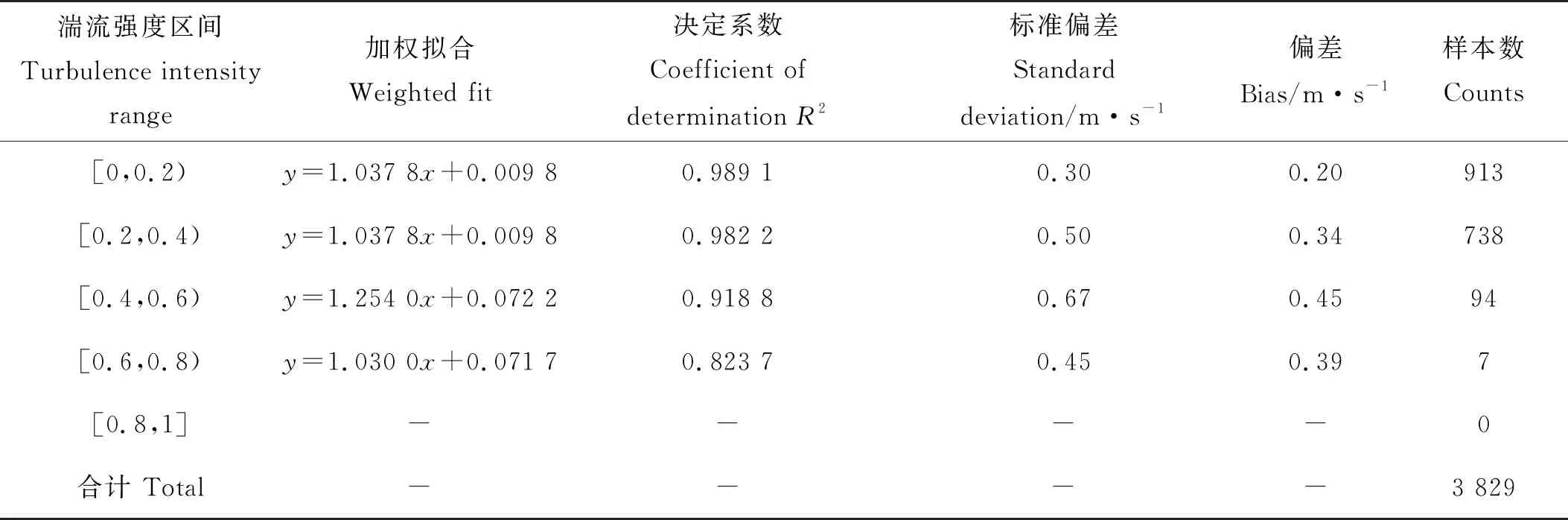
表2 不同湍流强度下的风速相关性分析

表3 不同高度的风速回归性分析

图8表示90 m高度风速和风向区间内平均值的相关性分析，图8(a)表示每个1 m·s-1的风速区间内三波束和五波束风速差的平均值相关性分析，图8(b)表示每个10°的风向扇区内三波束和五波束风向差的平均值相关性分析，误差棒分别表示该风速(a)区间或风向(b)区间内三波束方法计算值(蓝)和五波束方法计算值(绿)的标准偏差。可以看出，三波束方法反演的风速略大于五波束，随着风速增大，三波束的标准偏差有增大趋势。从图8(b)可以看出，两种方法反演出的风向一致性良好，决定系数和回归曲线的斜率均为1；在每个区间内，三波束方法和五波束方法的标准偏差都很小，均集中在回归曲线两侧。

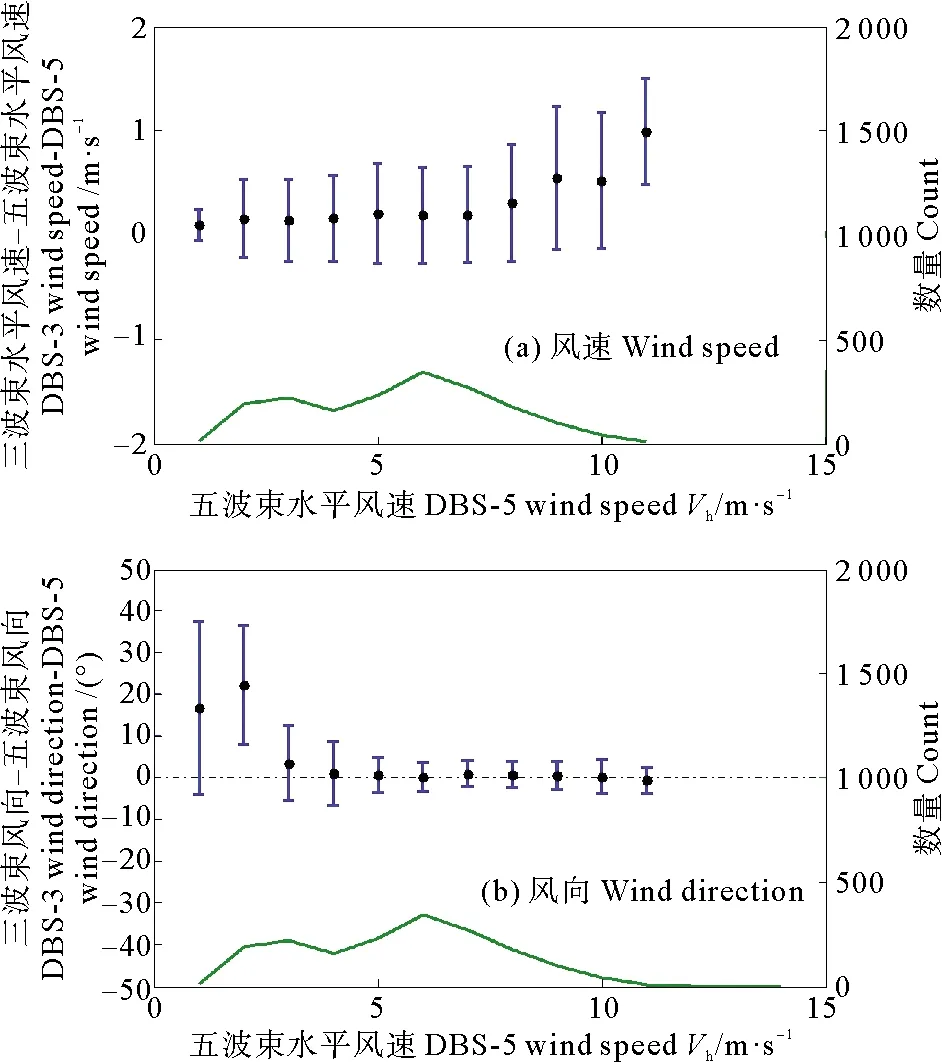
图7 每个区间内的平均偏差

除了北、东、垂直三个方向的波束进行反演外，同时对北、西、垂直(NWV)，南、东、垂直(SEV)和南、西、垂直(SWV)三种三波束组合进行了反演，并将反演结果与五波束进行了风速区间平均值的相关性分析。结果显示，风速区间平均值的回归曲线斜率分别为0.995 0(NWV)、1.030 8(SEV)、1.069 8(SWV)，风向区间平均值的回归曲线斜率均为1.000 0。

图8 90 m高度区间内平均值的相关性分析

4 结语

本研究利用三波束方法在中国海洋大学校园内对多普勒测风激光雷达Wind3D 6000实测数据进行了重新反演，经过信噪比和数据有效率门限阈值进行数据质量控制，与由激光雷达内置的五波束方法反演得到的标准产品level 2平均风廓线数据进行了水平风速、风向等风场特征参数的比对和分析。研究表明，两种方法在不同高度上的变化趋势和数值均呈现良好的一致性，三波束方法理论上能够在更短时间内反演出风场特征、提高数据刷新率，两种反演方法均适用于激光测风技术。

两种方法计算结果的差异与风速及湍流强度大小有关。两种方法计算结果在低风速区间和高风速区间的差异不同，且存在一定的变化趋势，这种趋势可能和该区间内数据量及风速本身大小有关。风速相关系数随湍流强度增大而减小，标准偏差随湍流强度的增大而增大。由于三波束与五波束两种反演方法使用的数据水平空间尺度相差约一倍(在90 m高度处水平空间尺度分别为51.96和103.92 m)，当湍流强度增大时，风场均匀性条件下降，这种现象在低风速时更为显著。但是，回归曲线的斜率和平均偏移量均在湍流强度[0.4，0.6)内达到最小和最大，造成这种现象的原因可能和数据量有关。湍流强度为[0.6，0.8)的区间内仅有7组数据，可能无法完全代表该湍流强度下的一致性。

本研究对实验数据进行了平均处理，三波束的数据刷新率优势仅通过理论分析，未进行实际的系统比对测量和数据分析，有待于进一步实验研究。对北、东、垂直三个方向的波束组合的反演结果进行了相对完整的讨论，其他波束组合的反演结果与北、东、垂直波束组合存在一定的差异但仍处于合理范围内。不同湍流强下三波束反演方法与五波束反演方法的差异，一方面可能是由于三波束方法中利用了垂直波束数据做反演、而五波束风速反演中垂直风速影响相互抵消，因此受到湍流效应和垂直激光束指向误差的影响更为明显；另一方面，目前的测量结果在湍流强度较强时样本较少，仍需在进一步的实验中采用更多样本开展研究。由湍流强度和风速大小引起的两种方法之间的差异及何种方法更准确、不同稳定性下的风场中三波束算法的具体优势、以及数据质量控制环节、系统测量误差等其他引起两者之间差异的原因也有待于进一步研究。