多充液贮腔航天器耦合动力学与姿态控制
2020-02-19岳宝增
刘 峰,岳宝增,唐 勇
(北京理工大学宇航学院,北京 100081)
0 引 言
随着现代航天器内的液体推进剂的质量占比不断提高,液体晃动动力学问题和有关的控制研究已经成为航天器总体设计中的核心问题之一[1-2]。在轨充液航天器内的液体晃动特别是大幅液体晃动具有比较低的固有频率,很有可能与航天器上的大型柔性附件及控制系统发生动力学耦合共振,这可能导致航天器结构的破坏或者姿控系统失效而使航天器姿态翻滚[3-4]。因此,现代航天工程中迫切需要建立准确、高效且适用性强的液体大幅晃动类航天器耦合系统动力学模型。
考虑到推进剂包含燃烧剂和助燃剂两种以上不同液体,航天器上往往需要携带多个卡西尼腔(或者球腔)。与单腔不同,各个贮腔尺寸及安装位置差异、推进剂消耗不均、不同液体特性等诸多因素,使得多个贮腔内的液体晃动与航天器主体之间的动力学耦合特性更为复杂。而关于这方面现有的研究极少,更多的研究工作有待进一步的完善。本文所建立的四充液贮腔航天器耦合动力学模型具备较强的适用性,模型中不仅考虑了航天器主体轨道平动与姿态转动,而且还包含有诸如贮腔的几何尺寸、布放位置、充液比及液体物理特性等反映耦合系统动力学特征的重要的工程参数。
Berry和Tegart[5]首次提出了等效液体晃动质心面模型,并基于此模型编制了相应的大幅晃动(Large amplitude slosh, LAMPS)Fortran程序,通过大量二维情形的低重力晃动试验验证了LAMPS程序在预测液体晃动力上的准确性。另一方面,文献[6-7]将二维质心面模型发展到三维情形,考虑单个贮腔作水平横向简谐运动时,通过对比由Fluent软件模拟得到的液体晃动力验证了质心面模型用于航天器贮腔大幅液体晃动分析的有效性;随后,采用牛顿-欧拉法将质心面模型整合到充液航天器耦合姿态动力学模型中,编制相应的Fortran程序对单贮腔航天器姿态机动问题进行了仿真计算,并与欧洲航天局2005年发射的液体晃动实验卫星(单贮腔卫星)的在轨测量结果进行了对比,验证了质心面模型应用于大幅晃动类充液航天器耦合动力学建模的可靠性。此外,文献[8] 进一步改进和发展了质心面模型。尽管如此,等效液体晃动质心面模型在等效液体黏性耗散力以及液体运动约束等方面尚有很大的研究空间[5]。
本文结合中国某型号航天器预研要求,基于已有的质心面等效模型,采用拉格朗日方法,系统地建立了任意复杂激励下四贮腔航天器刚-液耦合动力学精确模型,尽管在准确度上可能不及CFD-刚体耦合动力学模型[9],但是由于该模型所需求解的自由度远远低于CFD-刚体耦合动力学模型,能够实现与航天器控制系统进行快速高效的实时数据交互。然后,编制了相应的MATLAB仿真计算程序,考虑失重环境下航天器受复杂激励情形,通过对比Flow3D求解所得的液体推进剂产生的晃动力及晃动力矩结果,验证了所建模型的可靠性;同时,得到了特定工况下质心面模型的等效摩擦特性系数随贮腔充液比的经验关系。最后,考虑此类航天器在进行三轴稳定姿态机动时,液体晃动将可能对航天器的姿态运动带来强烈的扰动。为此,基于本文建立的耦合动力学模型,初步设计了相应的姿态机动补偿控制器,结果显示该补偿控制器能很好地抑制航天器姿态角速度的振荡。
1 四充液储箱航天器刚-液耦合动力学建模
1.1 质心面模型与储箱布局介绍
1975年,Berry和Tegart[5]提出了一种适用于求解微重力环境下液体晃动力的大范围运动及大幅晃动模型,该模型将贮腔内的所有液体等效为点质量并沿特定的约束表面运动,因此也称为质心面模型。如图1所示,针对航天器工程中主要采用的两类液体贮腔:卡西尼腔和球腔,质心约束表面(质心面)为一旋转椭球面,在腔体坐标系下质心面的曲面方程有如下表示:
(1)
特别地,对于球腔,有a=b。
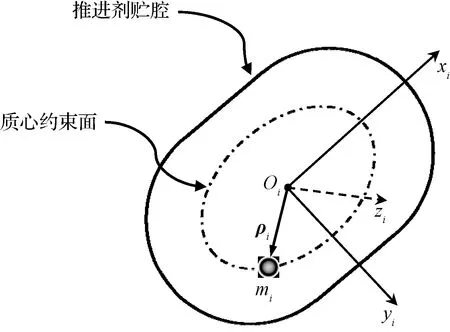
图1 质心面模型示意图Fig.1 Illustration of the constraint surface model forliquid sloshing


图2 航天器四贮腔布局与坐标系Fig.2 Four tanks layout in spacecraft and frames
1.2 系统运动描述
1)航天器相对于惯性参考系的转动
采用航天器整体坐标系相对于惯性参考系发生的转动来描述航天器的姿态运动,并使用无奇异的欧拉四元数描述法来定义航天器姿态矩阵
(2)

设航天器的转动角速度矢量在整体系中的坐标矩阵为
并由此规定任意矢量在整体系中的坐标表示方法。
由四元数表示的航天器姿态运动学方程则由如下关系式定义:
(3)

此外,重力加速度矢量在整体系下的坐标表示为:
(4)

2)航天器相对于惯性参考系的平动
航天器主刚体质心在惯性参考系下的位置和速度所对应的坐标矩阵分别记为
(5)
(6)
于是主刚体质心的绝对速度矢量在整体系下的坐标表示为
(7)
3)液体等效质心点的运动
记第i个液体质心点相对于惯性系的位置矢量在整体系下的坐标表示为
1ri=1rOi/N+1ρi
(8)

式(8)对时间求绝对导数,可得质心点的绝对速度在整体系中的坐标表示:
记Ri=1rO/C+1rOi/O+1ρi,质心点的绝对速度在整体系中的坐标矩阵最后可表示为
(9)

1.3 刚-液耦合系统动力学方程
本文采用混合坐标意义下的Lagrange方程[10-11]建立四充液贮腔航天器耦合动力学模型。建模过程需要计算航天器主刚体、储腔内液体及动量轮组成的耦合系统的动能和势能。设航天器主刚体的质量为mhub,关于其质心坐标系的惯性张量为Ihub;动量轮的惯性张量为Iw。
系统的动能由如下定义式给出
(10)
式中:mi是第i个质心点的质量,数值上等于对应贮腔内液体总质量;Ω是动量轮相对整体系的转动速度。
将式(9)代入式(10)并整理成矩阵形式:
(11)
只考虑系统的重力势能
(12)
将式(4)、(5)、(8)代入式(12)得到系统势能的矩阵形式:
(13)

于是,该耦合系统的Lagrange函数有如下表述:
(14)
1)航天器主刚体平动的动力学方程
以航天器主刚体质心的位置坐标和速度坐标表示的Lagrange方程为
(15)
式中:F是航天器系统受到的外力的合力在惯性参考系中表示的坐标矢量,其作用点位于主刚体质心。当不计入航天器主刚体及贮腔的质量时,由牛顿第二定律,F即表示四个贮腔内液体对航天器主刚体总的等效作用反力。
把式(11)、(13)同时代入式(14)后再代入式(15),最终得到描述航天器沿轨道平动的动力学方程:
(16)

2)航天器主刚体转动的动力学方程
伪速度(ω)下的广义Lagrange方程为
(17)
式中:M是航天器系统受到关于主刚体质心的外部作用力矩的合力矩在整体系中表示的坐标矢量。当不计入航天器主刚体及贮腔的惯量并不考虑动量轮作用时,由力矩平衡关系,M即表示四个贮腔内液体对航天器主刚体总的等效作用反力矩。
最终得到描述航天器姿态转动的动力学方程:
(1ω)×[Imb(1ω)+Iw(1ω+1Ω)+
(18)

3)质心点运动的动力学方程
以第i个质心点的位置坐标和速度坐标表示的Lagrange方程为
(19)
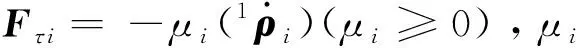
最终得到的描述质心点运动的控制方程为:
(20)
此外,动量轮的输出方程有如下表述:
(21)
1.4 求解质心面约束力
对于第i个贮腔,质心面在腔体坐标系下的曲面方程如式(1)表示,当质心点被约束在质心面上运动(联系运动)时,其沿曲面外法向ni的速度投影应始终为0,即有
(22)
并且有
(23)
式(22)对时间求微分可得联系运动的约束条件为
(24)
将式(23)代入式(24),得
(25)
再将式(20)代入式(25),可得质心点受到的法向支持力大小为
(26)
2 复杂激励下等效晃动力与等效晃动力矩验证
为了验证基于等效液体晃动质心面模型,根据我国某型号航天器预研的需要建立四充液贮腔航天器耦合动力学模型,这里,在航天器主刚体质心处施加全自由度的加速度激励,将液体所产生的作用于主刚体质心的晃动力及晃动力矩的模型计算结果与Flow3D计算结果进行对比。其中Flow3D计算方案主要包括:推进剂处理为不可压缩、黏性流体;使用单相流模型,气体部分仅提供环境压力,其密度相对液体很小,不进行动量计算;考虑表面张力;液固界面采用Navier滑移边界条件;先计算得到表面张力作用下稳态时的液面构型,再以此为初始条件导入给定激励进行计算。
给定主刚体质心同时受到1000 s的三维平动加速度激励与三维角加速度激励,它们的时程图分别如图3和图4所示。

图3 三维平动加速度激励时程Fig.3 Acceleration excitation in three directions

图4 三维角加速度激励时程Fig.4 Angular acceleration excitation in three directions


表1 推进剂特性参数Table 1 Characteristic parameters of propellant

表2 充液储腔球心位置坐标Table 2 Coordinates of the center of the tanks
本文给出了以下两种工况下的晃动力和晃动力矩的对比结果:工况1为各推进剂贮腔充液比均为20%(图5、图6);工况2为各推进剂贮腔充液比均为60%(图7、图8)。计算结果表明,充液比较高时,模型的计算结果更为准确,主要原因是由于当贮腔内液体越少时,同等水平激励下晃动的幅度越大,并且Flow3D计算显示液体出现更为明显的破碎。总的来说,晃动力和晃动力矩的对比结果体现出较高的吻合度,说明本文建立的四充液贮腔刚-液耦合动力学模型具有应用于航天工程实际的重大价值。

图5 晃动力:质心面模型vs.Flow3D(工况1)Fig.5 Slosh force: model results vs. Flow3Dresults(Case 1)
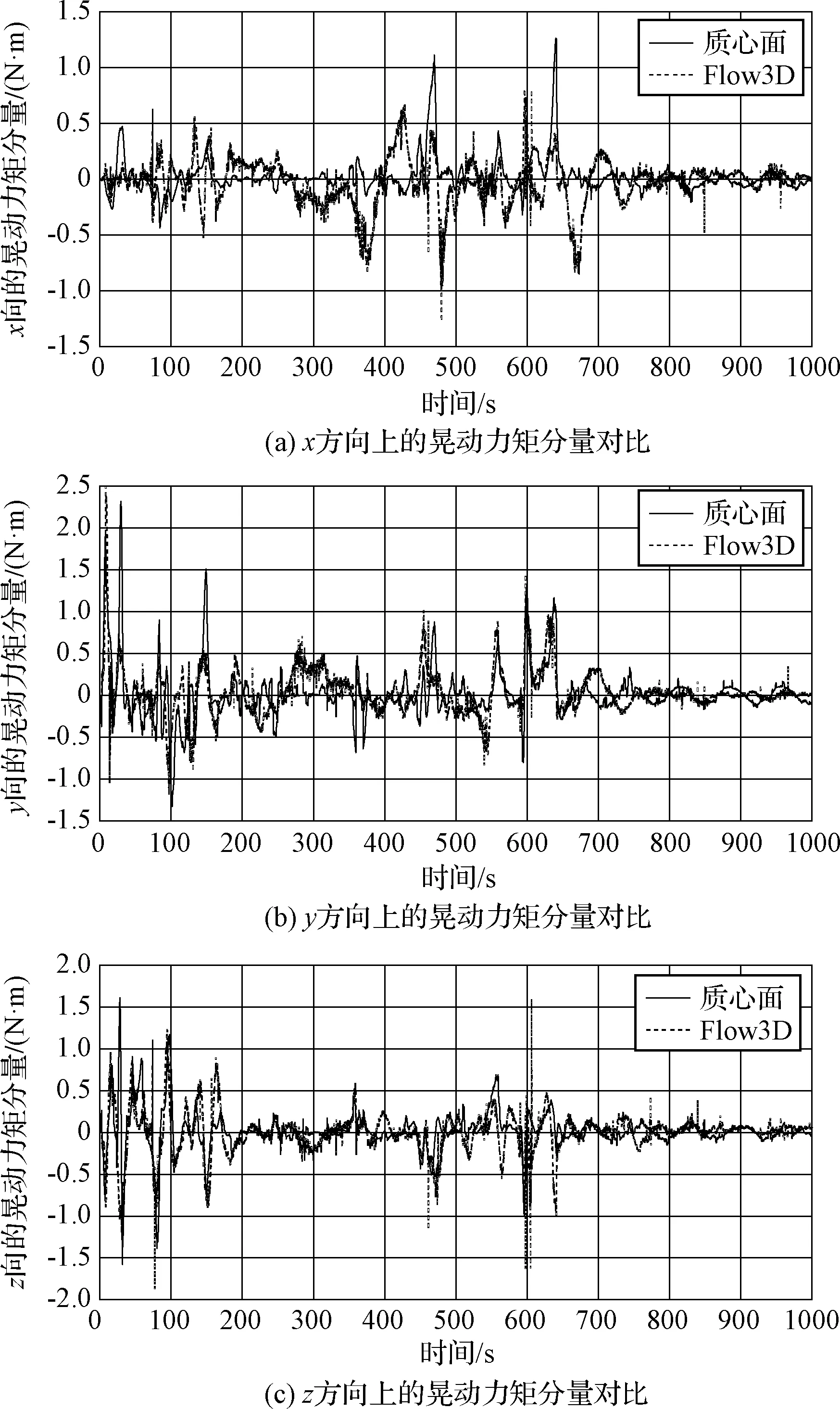
图6 晃动力矩:质心面模型vs.Flow3D(工况1)Fig.6 Slosh torque: model results vs. Flow3D results(Case 1)

图7 晃动力:质心面模型vs.Flow3D(工况2)Fig.7 Slosh force: model results vs. Flow3Dresults(Case 2)

图8 晃动力矩:质心面模型vs.Flow3D(工况2)Fig.8 Slosh torque: model results vs. Flow3D results(Case 2)

图9 等效摩擦特性系数与充液比经验关系Fig.9 Empirical relationship between μi andliquid-filled ratio
通过更多充液比工况下的对比研究,对于这里所给的球腔尺寸、液体黏性特性以及加速度环境,本文得到了质心面模型中的等效摩擦特性系数μi与充液比的近似经验关系如图9所示。
此外,本文基于质心面等效模型建立的多贮腔航天器刚-液耦合动力学模型在评估液体晃动力和晃动力矩时的计算效率远高于Flow3D计算流体动力学仿真软件。使用3.4 GHz的PC机,计算时长为1000 s,编制MATLAB四阶-五阶Runge-Kutta(ode 45)算法解算本文所建立的动力学模型只需2 h左右,而使用Flow3D仿真软件则需3天甚至更多时间(主要取决于计算网格尺寸相关)。
3 三轴稳定姿态机动设计
本节中,不考虑航天器轨道运动,启动动量轮对航天器进行文献[4]中的“rest-to-rest”形式(初始角速度与末态角速度均为零)的姿态机动,并研究机动过程中的刚-液耦合动力学特性。假定各个贮腔的充液比均为60%;航天器主刚体不受到任何外部作用力矩,即M=0。
研究发现,当航天器处于完全失重环境,且不受到任何强干扰(或激励)作用时,对航天器进行三轴稳定姿态机动过程中,主体姿态运动与液体晃动之间的动力学耦合效应不显著。进一步考虑在轨航天器的如下工况,即航天器主发动机点火(认为是一种强干扰)产生一个持续的推力使得航天器获得一个恒定的加速度,即航天器将处于一个等效的重力加速度环境,假定g=1 m/s2。航天器主刚体关于其质心坐标系的惯性张量为Ihub=diag(2700,1300,2300) kg·m2。
图10为采用文献[4]中的线性PD控制器:
Tw=kpεv+kd(1ω)
取kp=250,kd=2000,进行三轴稳定姿态机动时的航天器主体角速度响应。结果显示姿态机动过程中,贮腔内液体晃动将对航天器的姿态运动带来强烈的扰动,这种影响的主要原因是推进剂大幅晃动将造成航天器整体的惯性特性显著变化,同时产生较大的晃动扰动力和扰动力矩。这有可能引起航天器的结构破坏,甚至造成航天器姿态翻滚等严重后果,在工程实际中应设法解决或避免。
为此,初步设计了相应的姿态机动补偿控制器:
同样取kp=250,kd=2000,图11为机动过程中相应的角速度响应。结果表明,该类控制器能很好地抑制航天器姿态角速度的振荡,从而能有效避免实际工程中的潜在风险。

图10 PD控制下三轴稳定姿态机动角速度响应Fig.10 Angular velocity response under PD controller

图11 补偿控制下三轴稳定姿态机动角速度响应Fig.11 Angular velocity under compensation controller
4 结 论
本文基于已有的质心面液体晃动等效力学模型,采用拉格朗日方法,系统地建立了计及航天器质心平动、姿态转动与多贮腔内液体推进剂大幅晃动的刚-液耦合动力学精确模型。通过对比Flow3D求解所得的完全失重、复杂激励下液体产生的晃动力及晃动力矩结果,验证了所建模型的可靠性;同时,得到了特定工况下质心面模型等效摩擦特性系数与充液比之间的经验关系,具体呈现为二次函数的近似关系。最后,基于本文中建立的耦合动力学模型,研究了该类航天器在进行三轴稳定姿态机动时的推进剂晃动与航天器主体姿态运动之间的动力学耦合特性,主要表现为推进剂大幅晃动造成航天器整体的惯性特性显著变化,同时产生较大的晃动扰动力和扰动力矩,从而给航天器姿态运动带来明显的振荡影响;为此,本文设计了一类抑制姿态振荡的补偿控制器,并且计算结果验证了该控制器的有效性。
