金属包装容器二重卷封结构的泄漏机理及其实验研究

2020-02-18杨丹殷凤龙梁小冬廖洪波李尔康

兵工学报 2020年1期

杨丹, 殷凤龙, 梁小冬, 廖洪波, 李尔康

(西北核技术研究所, 陕西西安 710024)

0 引言

现代战争对军用包装的要求越来越高，促使传统的军用包装不断改进。为了降低成本、减轻装备重量、提高长期贮存的可靠性，一些新的包装理念和包装结构在军用包装容器的设计中得到大量应用[1]。在军用产品密封包装中，密封结构发生泄漏将导致包装环境的改变，是造成内装产品腐蚀、降解、变质、破坏和丧失使用功能的主要原因。大量研究表明，外界环境中的气氛侵入尤其是水汽通过渗透、泄漏等途径进入包装容器内部，长期情况下会显著改变内装产品的各项性能指标[2-8]。

金属包装容器因其优良的气体阻隔性能、良好的机械强度、可快速批量封装、成本相对低廉等优点，有望在弹药引信包装、火药安全存储、航空器材封存等军事领域获得应用前景[9-10]。研究解决金属包装容器的气体密封性问题，对于军用产品的长期可靠封存、保持相对稳定的物理性能具有现实意义。

在金属包装容器领域中，二重卷封结构作为最广泛的一种密封连接形式，其质量的优劣直接影响容器的密封性能。在金属包装容器的实际应用中，目前国内外通常以卷封厚度、叠接率、紧密度等制造工艺参数来定性判别对二重卷封结构密封效果的影响[11-13]，缺乏对二重卷封结构泄漏机理方面的相关研究。因此，系统地分析二重卷封结构的泄漏通道微观尺寸，开展二重卷封结构的泄漏机理及其量化研究，在指导金属包装容器的安全性和可靠性设计方面具有重要意义。

本文运用气体动力学相关理论，通过建立二重卷封结构泄漏模型，综合考虑气体的通道泄漏和渗透泄漏两种因素，定量研究了卷封结构几何特征尺寸和泄漏介质参数对二重卷封结构中气体漏率的影响。

1 二重卷封结构泄漏模型

1.1 二重卷封结构

金属包装容器上的密封形式包括罐身接缝和二重卷封。其中，罐身接缝属于永久密封形式，通常使用电阻焊工艺完成，其泄漏可忽略不计。二重卷封结构是金属包装容器罐身与罐盖、罐底的组合，以5层金属本体辅助密封材料咬合连接在一起的密封形式，如图1所示。密封胶预先喷涂在罐盖外沿上，通过二重卷封工艺压紧并充填于罐身与罐盖之间的结合面上，实现二重卷封结构的有效密封。气体经过二重卷封结构的泄漏途径有两种：一是气体经过密封胶的渗透，属于渗透泄漏；二是气体在密封胶和金属材料本体之间形成的微型通道中流动，属于界面泄漏。

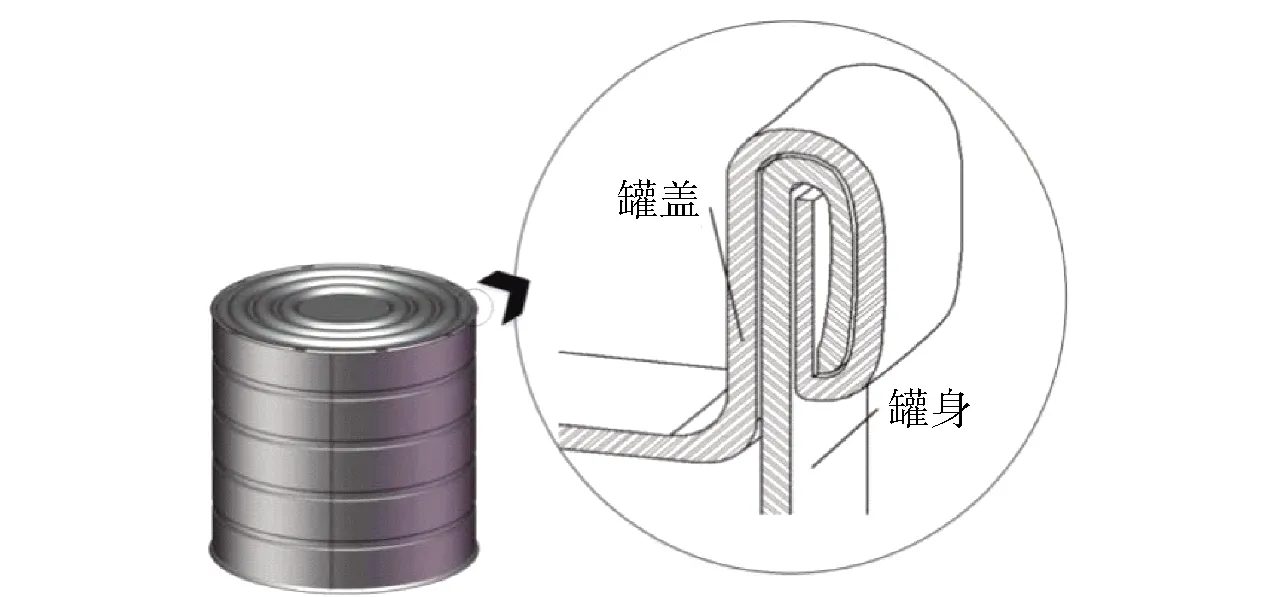
图1 二重卷封的剖面结构

1.2 二重卷封泄漏模型

将二重卷封结构沿包装容器的直径展开，使通道内流动方向与x轴正向一致，建立如图2所示的气体流动坐标系[14]。假设密封胶与罐身、罐盖之间的缝隙为矩形，则二重卷封结构的气体泄漏问题，可等效为气体在大长宽比矩形截面通道中的流动和渗透问题。矩形通道横截面的短边(即密封胶与金属本体之间的缝隙宽度)为a，长边(即包装容器的截面周长)为b，渗透通道宽度(即密封胶厚度)为σ，流动路径长度为E(即密封胶的宽度)，入口端气体压力为pi，出口端气体压力为pe.

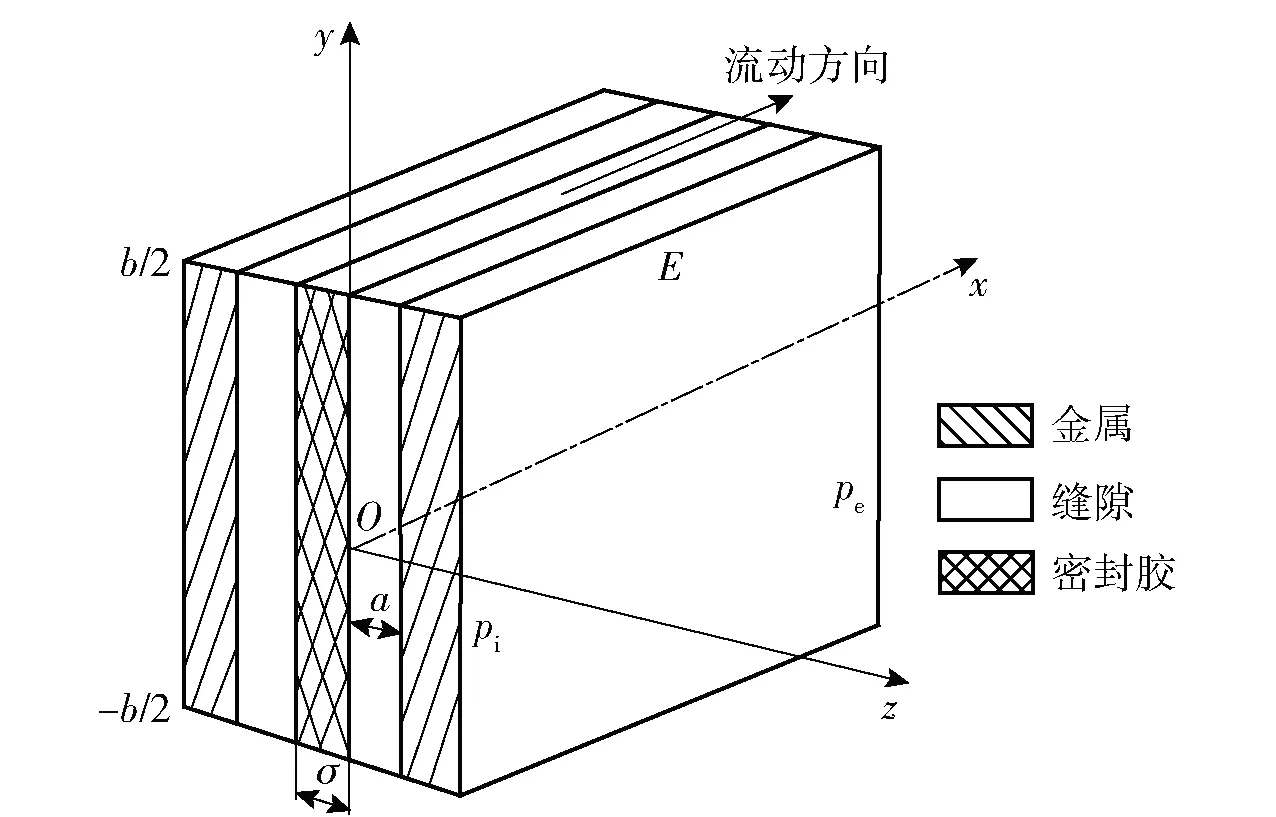
图2 二重卷封结构的气体泄漏模型

稳定状态下，黏滞流态气体流动的Navier-Stokes方程为

(1)

式中：u=u(y,z)为主流方向气体速度；μ为气体动力黏度；p为通道内气体平均压力。

两侧壁面上的流体速度为0 m/s，(1)式的边界条件为：y=±b/2，u=0 m/s；z=0，u=0 m/s；z=a，u=0 m/s.可解得截面通道上气体的速度分布为

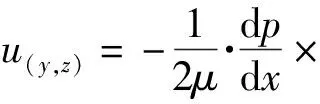
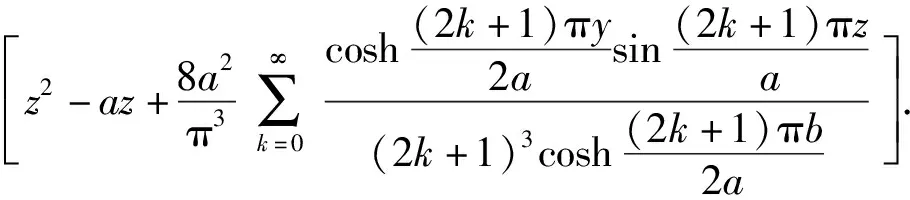
(2)

流经截面上的气体体积流量q为

(3)

(4)

解得

(5)

式中：Δp=pi-pe.由于在实际中，b为密封胶的长度(即罐的周长)，其值远大于a，则(5)式可近似为

(6)

单位时间流过缝隙的气体量(即气体漏率)Qi为体积流量与平均压力的乘积，则有

(7)

式中：Qi为密封胶与金属之间缝隙的气体漏率(Pa·m3/s)。

对于气体从密封胶中渗透所形成的泄漏量，影响因素为胶层的面积、渗透路径长度以及气体对密封材料的渗透系数，其漏率形式为

(8)

式中：Qp为气体在密封胶中的渗透漏率(Pa·m3/s)；d为包装容器直径(m)；p0为标准大气压力(Pa)；K为泄漏介质在密封胶中的渗透系数(m3(标况)·m/(m2·Pa·s))。

综合以上分析，矩形泄漏通道共两处，渗透通道一处，因此气体流经二重卷封结构的整体漏率为

(9)

式中：Q为二重卷封结构的整体漏率(Pa·m3/s)。

从(9)式可以看出，由密封胶渗透引起的气体漏率不可避免，二重卷封结构的整体漏率不小于气体在密封胶中的渗透漏率。当包装容器的直径和密封胶宽度确定时，控制二重卷封结构总泄漏量的关键是尽量减小密封胶和罐身、罐体之间的泄漏通道宽度，且该通道形成的漏率与泄漏通道宽度呈三次方关系。

2 二重卷封结构密封测试实验

2.1 实验条件

实验选取一批直径127 mm、高度120 mm、厚度0.25 mm的马口铁包装容器为测试对象。实验样品容器的底盖和顶盖均以二重卷封形式与罐身封接。二重卷封工艺参数如下：卷边厚度1.4～1.5 mm，卷边宽度2.9～3.1 mm，身钩长度2.1～2.2 mm，盖钩长度1.9～2.0 mm，叠接率不小于50%.以天然橡胶作为二重卷封结构的密封材料，胶层的平均厚度为0.05 mm，密封宽度为5 mm，长度取罐盖周长400 mm.二重卷封结构的密封性能测试方法为：对实验样品容器安装接口抽真空至20 Pa以下[15]，在容器外侧整体包覆集气罩并充入101 kPa压力的氦气，使用氦质谱方法测量包装容器的总漏率，如图3所示。

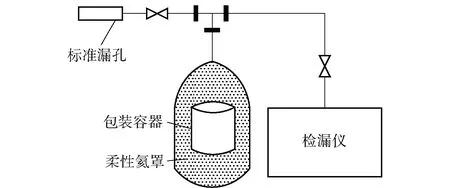
图3 二重卷封结构密封测试装置

通常金属包装容器的耐外压强度不大于80 kPa，在此条件下如果对包装容器抽至较高的真空度，会使其发生失稳变形，导致二重卷封结构密封失效，无法获得准确的密封检测结果。因此，为使容器达到内外近似一个标准大气压的强度要求，在样品容器外部采用了4道环形滚筋加强工艺，使其耐外压强度提高到120 kPa以上并测试验证。耐压强度测试装置由压力测试腔体、压力传感器、充气加压装置以及压力采集系统构成，压力数据采集频率为100 Hz，如图4所示。测试前，在大气压(101 kPa)下对样品容器进行封装，便于准确记录容器内部初始压力。测试时，在测试腔体中放置样品容器，密封好测试腔体的顶部法兰，向测试腔体和样品容器外侧之间的夹层中手动缓慢充入干燥氮气，保持夹层中的气体压力逐渐上升，同时通过安装在顶部法兰上的压力传感器监测充气过程中的夹层压力变化。当容器发生失稳时，其体积瞬间显著减小势必会使夹层压力曲线发生明显变化，此时样品容器的内外压力之差即为其耐压强度。

图4 样品容器耐压强度测试

图5给出了某次测试过程中腔体夹层的压力变化曲线，可得到该样品容器对应的耐压强度为138 kPa.重复性测试数据表明，样品容器的耐压强度集中分布在122～145 kPa之间，对其抽真空不会使二重卷封结构发生破坏变形，满足密封性测试时的内外压差要求(约101 kPa)。

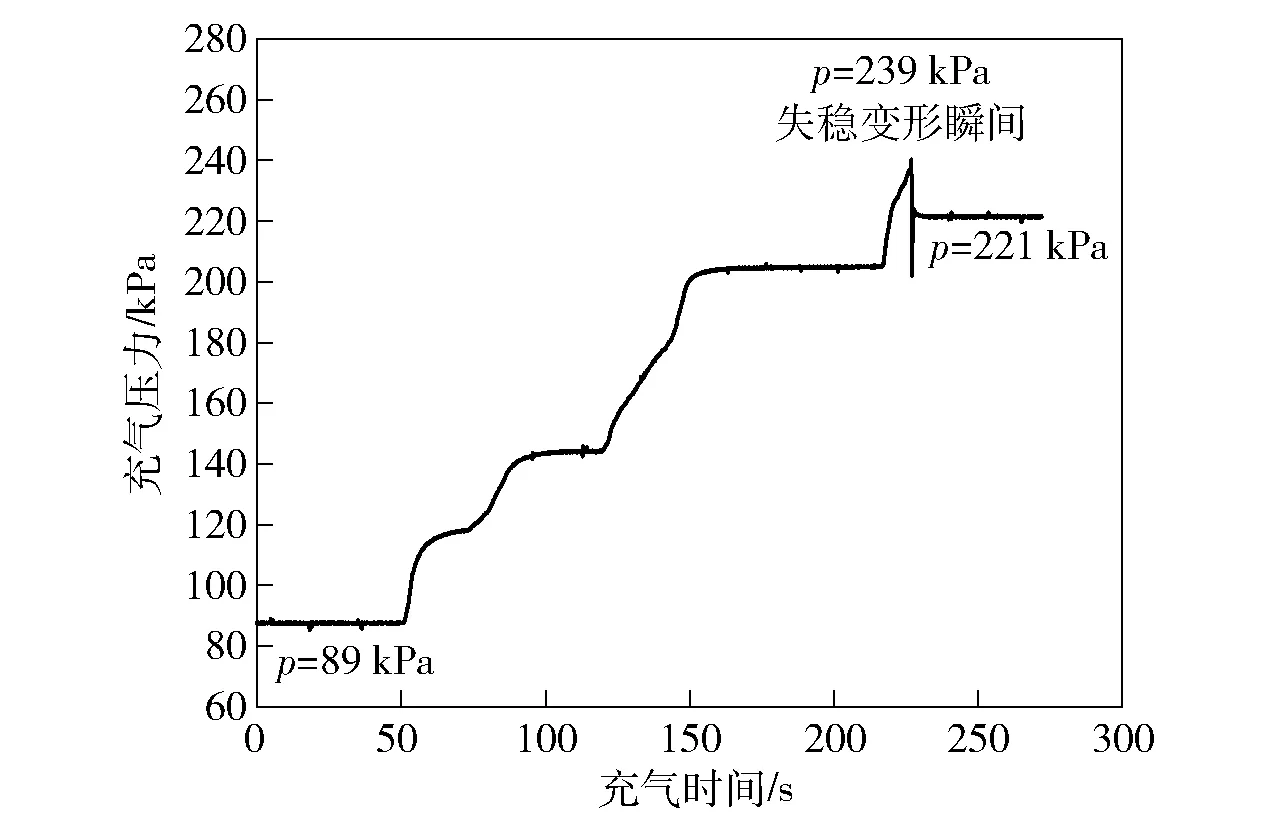
图5 夹层充气压力变化曲线

图6给出了上述相同规格样品容器的密封检测现场照片。在25 ℃室温条件下，氦气在天然橡胶中的渗透系数为2.25×10-11cm3(标况)·mm/(cm2·Pa·s)[16].根据上述参数，对于单道二重卷封结构，利用(9)式可计算得到氦气经过密封胶渗透形成的漏率为9.0×10-9Pa·m3/s.氦质谱检漏结果中共包含上下两道二重卷封结构的泄漏量，因此理论上样品容器的总漏率不小于1.8×10-8Pa·m3/s.

图6 样品容器密封测试

2.2 实验结果及分析

表1给出了10个样品容器的总漏率测试结果。样品容器的总漏率分布在1.7×10-8～5.2×10-8Pa·m3/s之间。考虑到测试过程中氦气的压力、浓度、标准漏孔等因素引入的不确定度，对于漏率最小的样品容器，可以认为密封胶层的气体渗透效应是形成泄漏的主要原因。切割包装容器的二重卷封结构，罐盖及罐底各选取3～4个切割点，并保持切割剖面完整清晰。使用扫描电镜对切割剖面进行观测，得到密封胶层的平均厚度约为53 μm，如图7所示。对于不同样品容器总漏率测试结果的差异性，主要原因可能是马口铁材料厚度的不均匀性(0.25 mm±5%)及其对两道滚轮卷封过程的影响，这同时也体现在前述样品容器耐压强度的差异性方面(122～145 kPa)。值得注意的是，实验中还发现样品容器泄漏的稳定时间普遍在20 min以上。

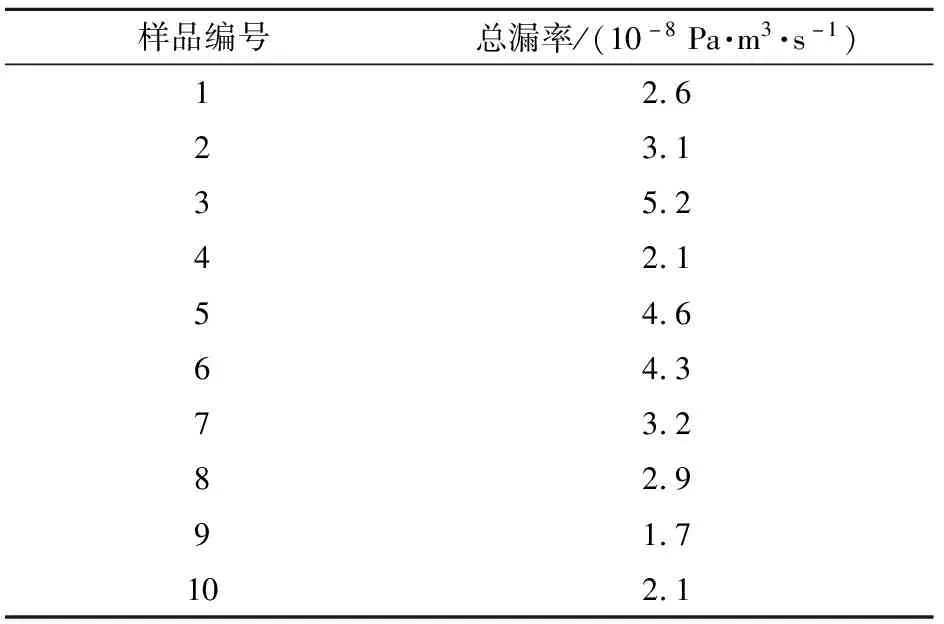
表1 样品容器总漏率测试结果

图7 密封胶层局部微观图

图8给出了密封胶和金属材料本体之间的泄漏通道宽度对应的包装容器的总漏率。从图8中可以看出，随着泄漏通道宽度的增大，样品容器的总漏率迅速上升。当泄漏通道宽度小于1 μm时，包装容器的总漏率可控制优于1.0×10-7Pa·m3/s.对于总漏率为5.2×10-8Pa·m3/s的包装容器，解算预判其泄漏通道的平均宽度为0.77 μm.图9给出了金属材料本体与密封胶层之间的缝隙微观照片，显示泄漏通道的宽度处于0.74～0.97 μm之间，与预期计算值符合较好。

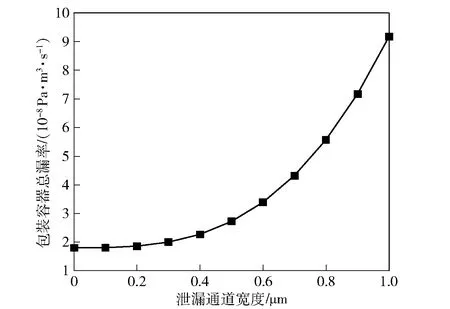
图8 不同泄漏通道宽度对应的总漏率

图9 金属材料本体与密封胶层之间的缝隙

由上述金属材料本体与密封胶层之间的缝隙测试结果可以看出，缝隙尺度在1 μm以下，其矩形流动面的当量直径为

(10)

流动缝隙a取1 μm，流动宽度πd取400 mm，可得到气体沿泄漏通道流动面的当量直径为2 μm，远小于流动路径总长(二重卷封结构的密封宽度)5 mm.在此条件下，氦气在泄漏通道入口处的Knudsen数约为0.1，符合连续性假设。因此，前述泄漏理论计算使用一维黏滞流模型是合理的，并且可以忽略气体流动的孔口效应。