溶洞分布对城轨交通盾构隧道 影响规律研究

齐明山 郭振坤 王春凯 柳献

摘 要：针对近年来广州、长沙、武汉及云贵等岩溶发育地区地铁工程现状，文章以贵阳市轨道交通 3 号线为工程背景，采用二维数值模型对溶洞分布影响进行模拟计算分析。经模拟计算分析，得出溶洞不同方位、不同尺寸、与盾构隧道不同净距以及在不同围岩等级中对隧道开挖洞室稳定性、隧道衬砌管片受力的影响规律，以确定贵阳市轨道交通 3 号线盾构施工中溶洞處理范围，为岩溶发育区城市轨道交通建设提供参考。

关键词：城市轨道交通;溶洞分布;盾构隧道;受力特性;处理范围

中图分类号：TU502

随着国内交通的不断发展[1-3]，盾构法隧道逐渐被使用于各种复杂地层条件，如上软下硬复合地层[4-5]、高水压[6]以及岩溶发育区[7-12]。穿越岩溶发育区的盾构隧道在施工阶段存在盾构机陷落、隧道偏线、突泥涌水等工程风险[13-15]，在运营阶段溶洞也会影响衬砌结构变形及内力分布，故在盾构掘进前需对隧道周边溶洞提前作加固处理[16]。苏伟?等[17]通过三维数值分析与模型试验确定侧部、下部溶洞对衬砌内力影响规律，并确定相应地层条件下的溶洞处理范围;苏锋等[18]运用三维数值分析提出溶洞的存在会引起管片出现纵向弯矩;潘清等[19]分析了溶洞直径、溶洞的方位、溶洞与隧道的净距对隧道洞周收敛以及衬砌管片的影响规律;李萍等[20]通过三维数值模型，考虑流固耦合效应，研究下伏溶洞对穿越上砂下黏地层隧道管片受力的影响分析。

目前，有关溶洞对盾构隧道开挖洞室稳定性、衬砌内力分布特性的影响规律等已有分析，但不同区域地质差异较大，为保证贵阳市轨道交通3号线盾构区段施工安全、防止地表塌陷并保证隧道在运营阶段正常运营，还需对3号线沿线溶洞发育情况及穿越地层条件进行分析。本文选用二维平面模型分析不同地层条件、不同方位、不同尺寸、与盾构隧道不同净距的溶洞对隧道开挖洞室稳定性及衬砌结构内力分布的影响规律，确定该地层条件下贵阳地区轨道交通溶洞处理范围，同时为其他岩溶发育区隧道建设提供支持。

1 工程概述

贵阳市轨道交通3号线一期工程盾构区段内，盾构隧道内径5.5 m，外径6.2 m，管片环宽1.5 m，管片厚度0.35 m，接头采用弯螺栓，环纵缝均不设凹凸榫。3号线起点为花溪环城高速公路北侧的桐木岭站，终点为乌当区洛湾站，全长43.19 km，其中地下线41.83 km，高架线0.71 km，过渡段0.65 km。沿线以中风化白云岩、泥质白云岩、中风化“砂糖状”白云岩、灰岩等可溶性碳酸盐为主。据钻孔揭露，钻孔岩石常见溶隙及溶洞，且溶洞多处于4级围岩，发育高度在1～5m之间，而80%以上发育高度小于3m。

经统计分析，各断面隧道埋深、地层类型、各地层厚度差异较大。为能分析溶洞位于隧道上方时对盾构隧道的影响，本文选取隧道上部有溶洞的皂角井站—太慈桥站区间段地层作为分析地层。在皂角井站—太慈桥站区间段取一典型断面，隧道埋深26 m，上覆0.8 m杂填土，16.6 m红黏土，其余均为中风化白云岩。

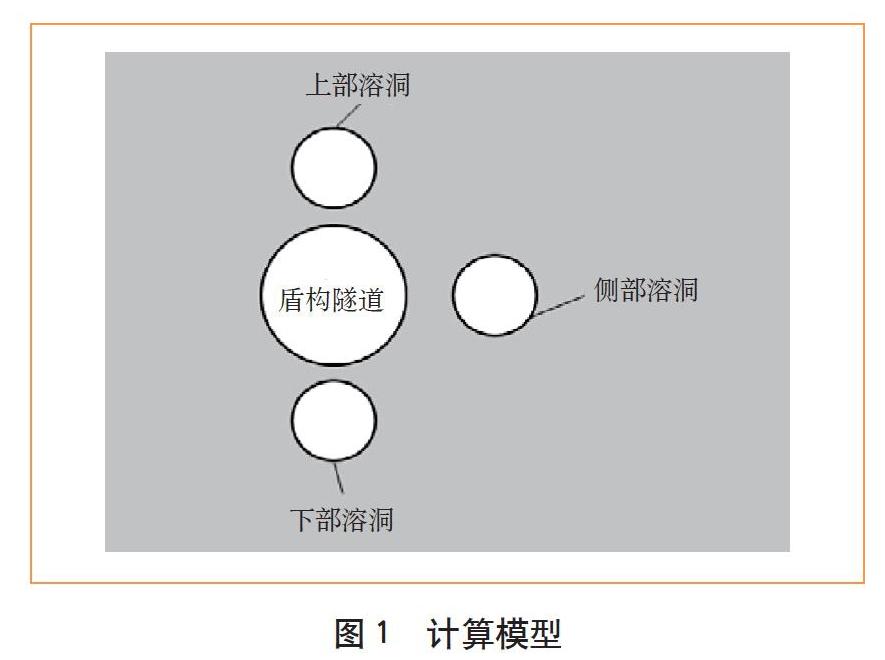
2 计算模型

2.1 数值模型

（1）模型尺寸。模型两侧与隧道底部均取5D（D为衬砌外径）作为边界，即模型尺寸定为66 m×62 m（宽×高）。

（2）模型边界。上边界取自由边界，左右边界约束水平位移，底部边界约束竖向位移。

（3）模型计算简化为平面应变问题。

（4）平面单元模拟地层，梁单元模拟隧道衬砌圆环。

计算模型见图1。

2.2 计算基本假定

（1）地层初始应力场为自重应力场。

（2）不考虑地下水。

（3）地层水平分层，假定均匀、各向同性，材料选用Drucker-Prager模型。

（4）溶洞简化为圆形，均无填充。

（5）考虑开挖后地层与衬砌协调变形。

2.3 计算工况

计算工况分为初始、开挖、衬砌3个工况，如图2所示（以顶部溶洞分析为例），具体如下。

（1）初始工况。仅溶洞存在，地层未开挖时计算初始应力场。

（2）开挖工况。开挖地层，应力释放50%。

（3）衬砌工况。拼装盾构衬砌圆环，应力释放50%。

2.4 计算参数

为准确分析隧道开挖时围岩变形规律，并较好地模拟围岩与衬砌环的相互作用，按照贵阳市轨道交通地勘报告并参考JTG D70-2004《公路隧道设计规范》附录A，计算参数取值见表1、表2。

3 溶洞方位对隧道影响

3.1 无溶洞

表3给出了无溶洞时开挖洞室收敛及衬砌内力情况，由表3数据可见，无溶洞时，开挖工况下隧道洞室拱顶下沉、拱底上浮量均为1.24 mm，最大拉应力出现在洞室拱底约为410 kPa，管片最大剪力16 kN。

3.2 上部溶洞

3.2.1 洞室收敛

表4 给出了溶洞在隧道上部时开挖洞室收敛情况，由表4数据可知，溶洞在隧道上部时，洞室拱顶下沉略有减小，下沉量大于拱底上浮量;拱底上浮量减小（最大减小量6%），随溶洞与隧道中心距离增加趋近于无溶洞时上浮量;洞室顶部及底部变形小于2 mm，洞室围岩稳定，计算未出现塑性区。

3.2.2 衬砌内力

图3给出了溶洞中心在隧道上部0.5D时开挖洞室衬砌内力情况，从图3数据可知，溶洞在隧道上部时，隧道顶部正弯矩减小，0°附近减小量最大，约为9.7 kN · m（减小50%），上半环其余位置正弯矩增加（或负弯矩减小）;衬砌轴力在隧道顶部增加47 kN（增加24%），隧道肩部及腰部轴力均减小，减小最大值约56kN;衬砌最大剪力15 kN，拱顶左右10°范围内剪力明显增加。

由此可见，对衬砌结构内力而言，上部溶洞存在的主要影响为，隧道顶部弯矩减小，轴力增加，表明溶洞的存在对结构受力而言无不利影响;剪力在隧道顶部左右10°附近出现明显变化。

3.3 侧部溶洞

3.3.1 洞室收敛

表5 给出了溶洞在隧道侧部时开挖洞室收敛情况，由表5数据可知，溶洞在隧道侧部时，洞室拱顶下沉、拱底上浮量均增加，最大分别增加15%、5%，随溶洞与隧道中心距离增加趋近于无溶洞时顶部和底部变化值;洞室顶部及底部变形小于2 mm，洞室围岩稳定，计算未出现塑性区。

3.3.2 衬砌内力

图4给出了溶洞中心在隧道侧部0.5D时开挖洞室衬砌内力情况，从图4数据可知，溶洞在隧道侧部时，隧道近溶洞侧腰部负弯矩最大，增加6 kN · m（增加30%），远离溶洞一侧腰部负弯矩增加5%;近溶洞侧，隧道肩部及脚部正弯矩增加，增加量约3 kN · m;对于衬砌轴力，隧道顶部和底部轴力变化在3%以内，近溶洞侧腰部增加88kN，增加12%，远离溶洞一侧腰部轴力增加40kN，增加5.6%;对于衬砌剪力，剪力最大值17 kN，增加6%，近溶洞一侧腰部衬砌剪力明显增加。

由此可见，对衬砌结构内力而言，侧部溶洞存在的主要影响为，隧道腰部弯矩增加，轴力增加，表明溶洞的存在对结构受力而言可能造成不利影响;剪力在近溶洞侧腰部上下10°附近出现明显变化。

3.4 下部溶洞

3.4.1 洞室收敛

表6 给出了溶洞在隧道下部时开挖洞室收敛情况，从表6数据可知，溶洞在隧道下部时，开挖洞室拱顶下沉量减小（最大减小14%），且随溶洞与隧道距离增加数值趋近于无溶洞时下沉量;对于拱底上浮，在隧道边界与溶洞中心相距0.5D时，上浮量增加7%，距离大于等于D时，数值均为1.22 mm，小于无溶洞时拱底上浮量;洞室顶部及底部变形小于2 mm，洞室围岩稳定，计算未出现塑性区。

3.4.2 衬砌内力

图5给出了溶洞中心在隧道下部0.5D时开挖洞室衬砌内力情况，由图5数据可知，溶洞在隧道下部时，隧道底部正弯矩减小，最大减小量约15 kN · m（减小70%），下半环其余位置正弯矩增加（或负弯矩减小），136°处正弯矩增加最大为7 kN · m（增加800%）;对于衬砌轴力，隧道底部轴力增加75kN（增加33%），隧道顶部轴力基本不变，其余位置轴力减小;衬砌剪力最大值18 kN（增加12%），隧道底部两侧10°范围内剪力发生明显变化。

由此可见，对衬砌结构内力而言，下部溶洞存在的主要影响为，隧道底部弯矩减小，轴力增加，表明溶洞的存在对结构受力而言无不利影响;剪力最大值在隧道底部左右两侧有所增加。

4 溶洞尺寸及与隧道距离对隧道影响

4.1 洞室收敛

4.1.1 溶洞在隧道上部

表7给出了不同溶洞尺寸、与隧道不同距离（溶洞中心距隧道边界）下开挖洞室收敛情况，从表7数据可知，溶洞在隧道上部时，溶洞较小时洞室拱顶下沉基本不变或减小，溶洞直径为4.5 m時增加30%;拱底上浮量减小（最大减小量13%），随溶洞与隧道中心距离增加趋近于无溶洞时上浮量。

4.1.2 溶洞在隧道侧部

表8 给出了不同溶洞尺寸、与隧道不同距离下开挖洞室收敛情况，从表8数据可知，溶洞在隧道侧部时，地层开挖后洞室拱顶下沉及拱底上浮量均增加，但拱顶下沉量大于拱底上浮量，最大值分别增加43%、16%，随溶洞与隧道距离增加而减小，数值趋近于无溶洞时下沉量;溶洞与隧道中心距离一致时，开挖洞室顶部及底部变形增量与溶洞直径正相关。

4.1.3 溶洞在隧道下部

表9 给出了不同溶洞尺寸、与隧道不同距离下开挖洞室收敛情况，从表9数据可知，溶洞在隧道下部时，开挖洞室拱顶下沉量减小，且随溶洞与隧道距离增加趋近于无溶洞时下沉量;相同距离下，溶洞尺寸与拱顶下沉量负相关，溶洞直径为4.5 m时，下沉量最小，减小32%;对于拱底上浮，在隧道边界与溶洞中心相距0.5D时上浮量均增加，溶洞直径为4.5 m时上浮量最大，增加12%，距离大于等于D时，均小于无溶洞时拱底上浮量。

由此可见，溶洞所在方位引起开挖工况下隧道洞室顶底收敛变化规律各异，就贵阳市轨道交通3号线所处地层而言，由于围岩变形模量较大，洞室顶部及底部变形小于2 mm，洞室围岩稳定，计算未出现塑性区。

4.2 衬砌内力

4.2.1 衬砌拉力

各方位溶洞引起的最大拉应力随溶洞与隧道距离变化关系见图6，由图6可知，溶洞在隧道上部和下部时，随着溶洞直径增加，衬砌结构最大拉应力减小（值均小于无溶洞时最大拉应力），且同一直径溶洞对隧道的影响基本不受距离影响;溶洞在隧道侧部时，在溶洞中心距隧道腰部距离小于D时，随着溶洞直径增加，衬砌最大拉应力增加，溶洞直径为4.5 m时最大拉应力为571kPa（增加40%）;距离大于D时溶洞尺寸对隧道影响较小，且与无溶洞时相比最大拉应力减小，有利于衬砌结构安全。

4.2.2 衬砌剪力

各方位溶洞引起的剪力随溶洞与隧道距离变化关系见图7，溶洞与隧道距离在D范围以内，衬砌结构剪力增加较大，尤其是溶洞在隧道侧部更加明显，剪力最大增加为无溶洞时的3倍。溶洞与隧道距离大于D时，侧部、下部溶洞对衬砌剪力影响可以忽略，剪力基本恢复到无溶洞时的水平，而顶部溶洞却造成衬砌剪力再次增加。

5 围岩刚度影响

考虑隧道穿越区间5级围岩的存在（强风化白云岩、强风化“砂糖状”白云岩），变形模量的减小，势必造成对开挖时围岩变形及衬砌结构受力的影响，故本节主要对溶洞存在时，围岩刚度（变形模量）影响进行参数化分析。经数据分析，5级围岩下除开挖洞室拱顶下沉量和拱底上浮量增加至130 mm左右外，衬砌结构内力在不同方位溶洞影响下的变化规律与4级围岩时基本一致，故此处不作赘述。下面分析3 m直径的溶洞在不同方位时对衬砌结构的内力影响，以确定不同围岩等级下贵阳市轨道交通3号线沿线溶洞处理范围。

图8给出了5级围岩下衬砌最大拉应力、最大剪力变化规律，由图8可知，在溶洞中心距隧道边界大于D时，溶洞的存在对衬砌结构受力的影响可控制在5%以内。

综上分析，对于贵阳地区4或5级围岩，为工程安全，适当增加溶洞处理范围，处理原则最终定为。

（1）隧道上部溶洞全部填充处理。

（2）隧道侧部及底部溶洞，与隧道净距6 m范围内溶洞应该处理。

6 结论及建议

（1）本文采用二维数值模型分析了不同方位、不同尺寸溶洞对隧道洞室及衬砌结构的响应规律，并以此确定了贵阳地区轨道交通溶洞处理范围。文中二维数值分析模型将溶洞存在对隧道的影响当作平面应变问题来考虑，虽然未能体现隧道不均匀下沉及纵向弯矩，但管片受力分析而言偏于安全。

（2）溶洞在隧道上部（下部）时，衬砌頂部（底部）弯矩减小，轴力增加，仅从衬砌最大拉应力来看溶洞的存在对结构受力而言无不利影响;但在上部（下部）附近会产生较大的剪力集中。

（3）溶洞在隧道侧部时，衬砌腰部弯矩增加，轴力增加，从管片最大拉应力来看，该类溶洞的存在对衬砌可能造成不利;就衬砌结构剪力而言，相同溶洞与隧道距离下，相比于隧道上下部溶洞，侧部溶洞造成的衬砌最大剪力值更大。

（4）就溶洞处理范围而言，隧道上部溶洞应全部填充处理;隧道侧部及底部，溶洞处理范围可定为与隧道净距6 m以内。

参考文献

[1]蒋树屏，林志，王少飞. 2018年中国公路隧道发展[J]. 隧道建设（中英文）， 2019，39（7）.

[2]孙钧. 国内外城市地下空间资源开发利用的发展和问题[J]. 隧道建设（中英文），2019，39（5）.

[3]洪开荣. 近2年我国隧道及地下工程发展与思考（2017—2018年）[J]. 隧道建设（中英文），2019，39（5）.

[4]潘建阁. 深圳复合地层对盾构隧道衬砌管片结构受力和变形的影响分析[D]. 北京：北京交通大学，2015.

[5]雷凯，莫海鸿，陈俊生，等. 上软下硬复合地层中盾构隧道管片受力变形性态研究[J]. 广东土木与建筑，2016，23（8）.

[6]周济民，何川，肖明清，等. 狮子洋水下盾构隧道衬砌结构受力的现场测试与计算分析[J]. 铁道学报，2012（7）.

[7]李鸿博，贾峰，李靖，等. 大连地铁5号线跨海隧道设计关键技术[J]. 岩土力学，2017，38（增1）.

[8]何高峰，罗先启，范训益，等. 南宁地铁2号线岩溶风险分析和处理原则[J]. 铁道标准设计， 2018，62（5）.

[9]徐正宣. 深圳地铁3号线工程岩溶洞穴勘察及病害处理技术研究[D]. 四川成都：西南交通大学， 2008.

[10] 龙艳魁. 长沙地铁1号线工程岩溶洞穴稳定性及其病害处理研究[D]. 湖南长沙：中南大学， 2012.

[11] 易介民. 岩溶地区地铁隧道稳定性的数值模拟分析[D]. 广东广州：华南理工大学，2011.

[12] 许凯. 隐伏型岩溶盾构隧道运营期结构稳定性研究[D]. 广东广州：华南理工大学， 2017.

[13] 王宁，阎长虹，邵勇，等. 南京地铁3号线岩溶发育规律及其对工程建设的影响[J]. 江苏建筑， 2011（6）.

[14] 高墅. 地铁工程盾构区间岩溶地层处理对比及探讨[J]. 国防交通工程与技术，2018，16（1）.

[15] 乌健. 广州地铁岩溶区盾构施工地层变形特性研究[J]. 铁道建筑，2012（8）.

[16] 刘晨. 盾构法在贵阳岩溶地区应用风险及措施[J]. 上海建设科技，2017（6）.

[17] 苏伟. 溶洞对地铁隧道结构力学特性及围岩压力影响的研究[D].湖南长沙：中南大学，2008.

[18] 苏锋，郑文博. 岩溶对地铁隧道围岩稳定性影响的数值模拟[J]. 人民长江，2013，44（3）.

[19] 潘青，张清照，赵璟璐，等. 岩溶分布规律对盾构隧道稳定性影响分析[J]. 现代隧道技术，2018，55（增2）.

[20] 李萍，李威，文武双，等. 下伏溶洞对穿越上砂下黏地层隧道管片受力的影响分析[J]. 铁道建筑， 2018，58（4）.

收稿日期 2019-09-23

责任编辑 朱开明

Study on influence of karst cave distribution on urban rail transit shield tunnel

Qi Mingshan， Guo Zhenkun， Wang Chunkai， et al.

Abstract： In view of the current situation of metro projects in karst developed areas such as Guangzhou， Changsha， Wuhan， Yunnan and Guizhou in recent years， this paper takes Guiyang rail transit line 3 as a project study case， and uses two-dimensional numerical model to simulate and analyze the influence of karst cave distribution. Through the simulation calculation and analysis， it works out the influence patterns of different directions and dimensions of the karst tunnel， different clearance from the shield tunnel and different surrounding rock grades on the tunneling stability and the stress of the tunnel lining segments， so as to determine the affected area of the karst shield tunneling of Guiyang rail transit line 3， providing reference for the urban rail transit construction in the karst developed area.

Keywords： urban rail transit， karst cave distribution， shield tunnel， stress characteristics， affected area