“从人”定价标准下商业车险保费的多因子影响分析——来自国内A保险公司保单数据的实证检验

陈若愚，张 莹，石洪波

（1.安徽财经大学金融学院，安徽蚌埠233000；2.中央财经大学金融学院，北京100081）

随着保险知识的普及和保险意识的增强，越来越多的人们开始意识到保险对于人身安全和财产安全的重要性。截至2019年7月，我国当年度机动车辆保险原保费收入4 579亿元，已达到总财产险原保费收入7 672亿元的59.68%。除了交通管理部门强制要求的交强险以减轻交通事故带来的严重损失之外，车损险、意外险、盗抢险等商业车险产品的保费收入也在逐年递增（见图1）。

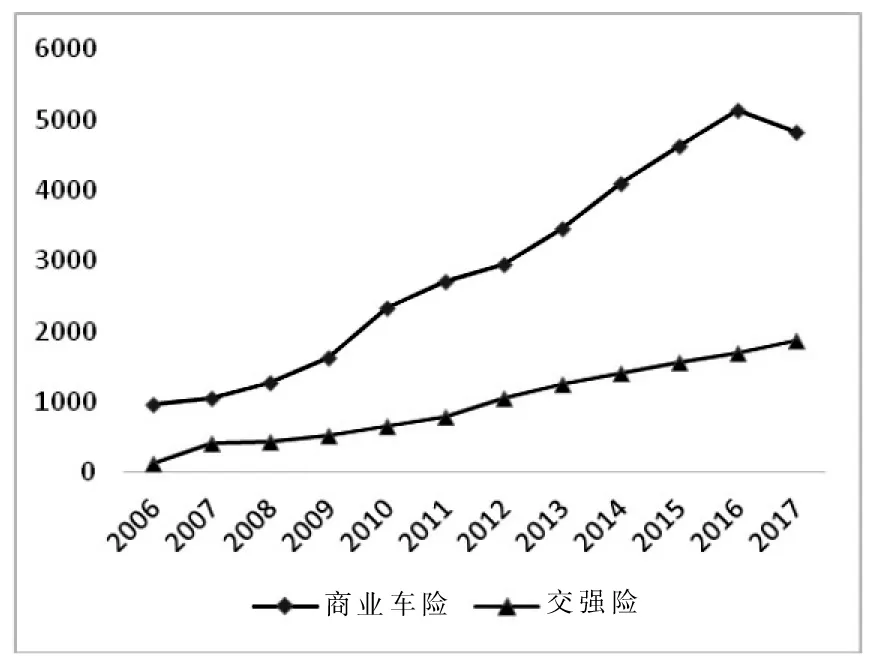
图1 交强险和商业车险纯保费收入

然而，根据银保监会数据公布，2018年我国机动车辆保险理赔纠纷投诉28 820件，占财产保险公司理赔纠纷投诉总量的74.20%。投诉主要反映保险机构承保时未充分说明保险义务、责任免除、定损金额、理赔时效等问题而引发的理赔争议。其中，很大的原因在于车险前端销售服务过程中的专业性匮乏，更有甚者，保险业务员对于客户风险等级及承受能力的定位模糊，反而以变相的车险回扣作为物质利诱条件，为客户推荐高费用的保险产品，一味追求保单成交量以达到业绩目标，漠视车险产品风险保障职能的本质。因此，为保证潜在车险客户更加详细地了解保费定价的影响因素，以选择出适合自身的车险产品，避免出现销售误导情况，减少不必要的保险合同理赔纠纷，同时为便于保险代理人在简要了解客户实际情况之后，客观定位客户人群并为其选择合适的车险产品，从而提高服务质量，促进车险行业正本清源，探讨商业车险保费大小与各影响因素间的定量关系并给出相关建议是很有必要的。

一、文献综述

Rothschild和Stiglitz（1976）在经典保险市场逆向选择理论模型中提到，保险市场存在严重的信息不对称现象。因保险人难以准确评估单个客户的风险等级，无法根据“一车一险一价”的保费收取标准为其提供等价的保障，只能根据风险均值与出险概率设置相应的费率系数。对于风险系数小、出险概率低的客户来说，其在保险市场上充当了为高风险、易出险客户分摊风险的角色。长此以往高价收费而低风险的客户就会远离商业车险市场，出现典型的逆向选择效应，将直接导致车险赔付率上升，造成理赔困难的现象。

郭振华［1］从行为保险学的角度提出，人们不愿意购买保险导致保险市场供求不平衡的主要原因在于忽略小概率风险和过度短视。对于车险市场上不易出现交通事故或者厌恶风险的人群来说，他们往往倾向于低估自身行驶风险，不购买商业车险或者选择保额较低、保费较少等不适合自身实际情况的车险产品。该理论认为消费者低估自身风险是保障型车险市场供给失灵的原因所在。

正因为车险市场的逆向选择以及消费者的风险低估，造成优质客户资源稀缺且难以甄别，各大保险机构不得不采用价格竞争和夸大宣传等方式夺取客户。其中，市场返佣、给予额外物质利益的现象层出不穷。王鹏［2］认为目前车险产品同质化严重，保险业务员返佣、赠送礼品吸引潜在客户的违规现象还会持续很长一段时间。这无疑严重阻碍了车险市场费率化改革的进程和长远健康的发展。

苗力［3］认为随着数字经济时代的到来，消费者对于保险产品的差异化、个性化、场景化提出了更高的要求，保险机构的企业运营模式也应由以企业为主导转向以利益相关者（即销售人员与用户）为主导。在保险机构销售人员方面，陈贤［4］明确指出，缺乏服务场景和用户黏性的销售渠道依靠佣金差生存的局面将很快被打破；业务员身为产品销售的主力军，以消费者为中心优化车险服务是保险公司长远竞争的终极武器。在潜在保单客户方面，陈秉正［5］认为，相对于广大人民群众日益增长的保险需求，车险产品有效供给明显不足。其中，一大重要原因在于销售过程中客户难以明确定价机制、无法选择出合适的产品。姚睿［6］等人也提出保险机构的前、中、后台人员需要了解精算定价模型的逻辑和使用方法，为公司打造统一的对话平台。但学者们在一针见血地提出该问题之后，并未为保险公司销售人员以及准车险客户分析影响车险保费大小的因素，客户仍然难以在购买洽谈期间选择合适的保险产品，问题并未得到实际解决。

特别值得注意的是，大多数学者都是基于车险费率精算研究车险定价因素，并改进定价模型的。孟生旺［7］选取了车辆年行驶里程、车型、行驶地区、NCD系数为影响因子，采用广义线性回归模型并选取对数联结函数对索赔频率、次均赔款及纯保费进行了拟合。康萌萌、刘素春［8］在前者的基础上认为广义线性模型低估了参数的标准差，应采用广义估计方程进行建模分析。蒲适、陈秉正［9］引入“索赔频率、索赔类型、索赔额”结构代替“索赔频率、索赔额”结构的多元个体损失模型进行聚类分析，以更公平地实现车险纯保费差异化定价。然而，却鲜有学者从前端的保险产品销售环节出发，为承保过程中的个体双方提供便于理解的定价模型。因此，为解决这一问题，本文从前端销售入手，以车险保费的“从人”定价标准为准则，旨在通过车险保费影响因素的定性分析以及模型的定量说明，为产品销售双方的客户定位和产品选择提供参考。

二、多因子影响因素的机制分析

（一）车辆因素

近年来，随着商车费改的不断推进，行业精算的不断发展，粗放式的仅根据车辆型号、车辆价值来确定保费的定价模式显然是极度不科学的。但投保车辆的基本情况对于车险保费的影响是必不可少的。不同品牌、不同型号、不同性能的车辆对应的价值和出险概率也大不相同。诸如新车购置价、车辆使用用途、车辆座位数情况等是反映车辆特征的基本因素。其中，关于新车购置价方面，有学者提出以车辆现值作为计量因素更为科学。但由于销售面谈过程中的车辆现值确认困难，后文选用新车购置价作为车辆影响因素较为便捷实际。

（二）驾驶人因素

1.性别

张圆等人［10］研究指出，女性驾驶员的交通事故死亡率低于男性驾驶员，但事故发生率高于男性驾驶员。由于性别常常决定着性格差异，男性驾驶员在驾驶过程中，超速、超车、酒后驾驶、不使用安全驾驶工具的行为时有发生。女性驾驶员因生理、心理等方面的因素，在行车过程中较为平稳谨慎，但由于技术的限制，小摩擦事故比男性频发。因此，有必要将性别因素纳入基于风险分类的保费影响因素分析体系之中。

2.年龄

由于家庭组成情况、人生阅历以及责任感强度的差异，年龄较小的驾驶人往往在车辆行驶过程中更加随心所欲，而年龄较大者更趋向于平稳驾驶。裴玉龙等人［11］通过采集不同年龄驾驶人的脑电信号的研究结果表明，青年人较于中年人更容易出现驾驶疲劳的生理情况，这在一定程度上增加了年龄较小驾驶人的出险概率。当然，老年人因其反应能力、精神精力的衰退，出险概率应高于青年和中年驾驶人。通常认为，行车风险与年龄大小呈现U字形分布。［2］

3.立案件数

显而易见，保险人在给车辆承保过程中，应十分清晰地了解该车辆之前严重的交通事故发生情况。车辆立案件数在一定程度上反映了车辆性能，究其立案原因，也能反映出驾驶人的驾驶行为习惯。对于立案件数多的客户，保险人所承担理赔的风险也愈大，相应地所收保费也会相对较高。而对于无立案件数甚至连续多年无出险记录的客户，保险公司会为其提供优惠策略，将风险与责任相匹配。

4.已决赔款

已决赔款能反映客户前期的驾驶行为导致的赔付率情况，除了便于保险公司判别客户的风险等级之外，也有利于保险业务员为其推荐合适保额大小的车险产品。对于事故频发、已决赔款高的客户来说，提高保额是理性的选择。同时，保额的提高和NCD系数的上升也会导致客户所交保费的增加。

三、实证分析

（一）数据来源及处理

本文保单数据均来自于数学中国网站。为了便于研究，本文在上万条保单数据中将缺失客户信息的空白数据剔除，根据控制变量原则，保证除需研究的因子之外其他影响因素的一致性，以尽量消除其他因子对研究带来的偏差影响，从而选取出2018年购买商业车险的省内（即仅在省内驾驶出行）家庭自用汽车个人客户的数据。

（二）变量选取和控制

对商业车险保费大小进行多因子分析时，选取签单保费为被解释变量并设置为Y，根据各因子之间以及与被解释变量的线性相关系数分析，选取新车购置价、被保险人年龄及已决赔款为解释变量并依次设置为X1、X2、X3。然后使用控制变量法设置其他相关变量为一固定值，如控制车险保额为30万元、针对车辆为家庭自用型、客户类别为个人而非机构以及对于车辆损失、盗窃、抢劫、车上人员均进行投保等，以减少其他因素对实证研究造成的影响。除此之外，本文将不可忽视的车辆事故立案件数和被保险人性别设置为虚拟变量的形式，以便进行更好的定量分析。变量选取和设置如表1所示。

（三）实证方法

运用计量经济学软件Eviews9.0对筛选处理后的因素和数据进行相关分析及回归分析，并通过相关系数检验、拉格朗日检验（LM检验）、布罗斯-帕甘-戈弗雷检验（BG检验）分别判定回归模型的多重共线性、自相关性以及异方差性。

首先，通过添加虚拟变量，不断重新设置和调整虚拟变量的斜率式和截距式的模型形式，最终选择混合式回归模型：

从而得到较为优化的回归模型结果。然后，需要对初步得到的回归模型进行检验。居于首位的计量检验是多重共线性的检验，根据各因子间的相关系数大小以及方差膨胀因子

其次，通过DW检验判别准则以及LM检验构建残差的辅助回归模型的方法来检验模型的自相关性。当DW准则检验一阶自相关性而落在不可判别的区域内时，默认LM检验的滞后期为2，借助辅助回归模型的显著程度间接判定原模型的自相关性。

最后，除了残差分布图的变化趋势，借助BG检验构建残差平方的辅助回归模型及受约束的F统计量和LM统计量的方法［10］，采用P值检验法亦可检验原回归模型的异方差性。

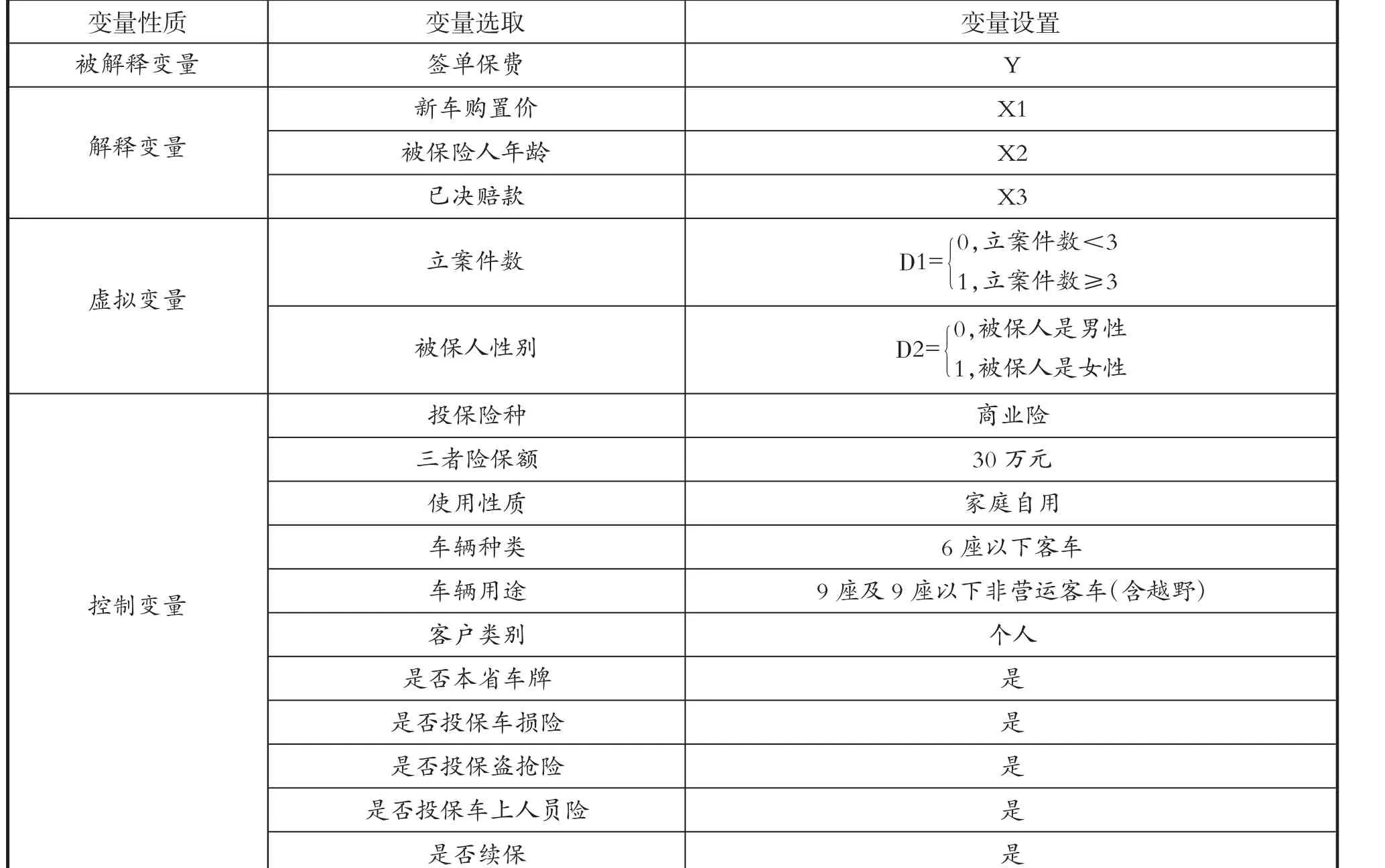
表1 变量设置表

（四）实证检验

1.模型的多重共线性检验

从表2的相关系数可知，各解释变量之间不存在严重的多重共线性。为进一步准确检验，笔者建立了辅助回归模型，采用最小二乘估计法（OLS）建立每个解释变量对其余解释变量的辅助回归方程，所得三个辅助回归模型均未通过统计意义上的t检验、F检验和R2可决系数的检验，且各辅助模型的方差膨胀因子都显著地小于10，说明商业车险保费的多因子回归模型并不存在多重共线性。

表2 相关系数检验表

2.模型的自相关性检验

根据上述多因子模型的估计结果可知

DW=1.557 147，取 α=0.05，结合统计量临界值和DW决策规则得到dL=1.10＜DW=1.557147＜du=1.66，（n=24，k=3），落在无法判定的区域内，则进行LM检验。根据表3结果可知，LM检验辅助回归模型et=b0+b1x1t+ … +bkxkt+ρ1et-1+ρ2et-2+ … +ρpet-p+υt的参数统计量LM（2）=nr2=1.345 021＜（2）=5.99 147，其临界概率P=0.510 4＞0.05，即表明残差辅助回归模型不显著，原模型不存在自相关性。

3.模型的异方差性检验

表3 LM检验表（Breusch-Godfrey Serial Correlation LM Test）

BG检验结果如表4所示，辅助回归模型e2t=a0+a1x1t+a2x2t+…+akxkt+υt的 LM（2）=nr2=16.363 95＞（2）=5.991 47，且取 a=0.05，F 统计量的临界概率 P=0.004 1＜0.05，说明残差平方的辅助回归模型是显著的，则原模型存在异方差性。

表 4 BG 检验表（Heteroskedasticity Test：Breusch-Pagan-Godfrey）

4.模型修正

对于存在异方差性的回归模型，采用加权最小二乘法对原模型予以矫正。加权的基本思想是：在采用最小二乘法时，对较小的残差平方赋予较大的权数，对较大的残差平方赋予较小的权数，对残差进行校正，提高参数的精度［12］8。本文通过生成权数变量w=估计模型，得到如下回归结果：

通过比较，引入权数变量w=1/et2得到的模型解释能力更强，参数精度更高，且再一次进行异方差性的检验，显示矫正后的模型已经不存在异方差性。

四、结果分析

由表5可知，新车购置价和已决赔款对于签单保费的决定程度不受研究中虚拟变量的影响。新车购置价越高，车辆因出险事故的维修成本也越高，保险公司理赔承压，因而签单保费均较高。已决赔款总额越高，说明出险次数较多或者事故严重程度较大，客户的总体风险评级偏向于高风险，对于保费大小起到一定的正向影响。但在不同性别和立案件数情况下，驾驶人的年龄对于签单保费具有不同的影响，甚至影响方向都大有差异。

表5 各因子对于保费大小的影响

五、相关建议

本文通过对新车购置价、被保险人的年龄、性别、已决赔款、立案件数五个因素的分析，确定了其对于保费大小的边际影响程度，这对车险产品的定位销售和精细服务提供了部分价值。据此，可以提出以下建议：

首先，由于基于精算式的车险产品费率厘定过于复杂，无法在前端销售时满足保险业务员和投保人实际的疑问需求，因此，保险机构业务员在为潜在保单客户推荐车险产品时，可以从客户的个人实际情况出发，根据以上研究为客户专业细致地分析影响其所需缴纳保费的因素，评估其风险水平，为客户选取合适的车险产品，减少车险销售纠纷和理赔争议，以充分发挥财产保险的经济补偿职能，更好地维护长期客户，提高续保概率。

其次，准车险客户在选择和组合商业车险的时候，亦可以根据被保险人的年龄、性别、已决赔款、立案件数、平时的驾驶习惯等因素自行评估自身风险，结合车险保费大小的多因子模型及自身现实情况了解所需车险种类，提前获悉可接受的保费承担范围，实现成本最小、所获经济保障最大的车险险种组合。

有别于传统的亲缘销售、回扣销售、误导销售模式，在这种信息不对称现象减弱的专业化销售模式下，潜在客户对于产品定价和格式条款的了解不断加深，这对保险推销员提出了硬技能上的要求。随着产品定价的信息披露力度加大，前端销售双方相互促进相互监督，我国保险行业有望加速走上规范化、专业化、精细化的发展道路。