基于样本依赖代价矩阵的小微企业信用评估方法

张 涛，汪御寒，李 凯，张玥杰

（1.上海财经大学信息管理与工程学院，上海200433；2.上海财经大学上海市金融信息技术研究重点实验室，上海200433；3.复旦大学计算机科学技术学院，上海200433；4.复旦大学上海市智能信息处理重点实验室，上海200433）

随着金融业的发展，其服务范围和方式日益丰富。联合国于2005年提出普惠金融的概念，小微企业是普惠金融重点关注对象之一。我国近年来加大了对小微企业的扶持力度，鼓励商业银行对小微企业的借贷服务。小微企业本身暗含较高的风险，建立科学的信用评估系统对风险进行精准判别，对金融机构来说至关重要。一般金融机构对小微企业风控严苛，导致可用的违约客户数据集规模较小，类别不平衡程度较高。基于这类信息不充分的数据集，构建泛化性能较好的模型具有较高的理论和应用价值，有助于金融机构识别劣质客户，更好地服务优质客户，从而促进市场经济的发展。

国内外对于信用评估已有较丰富的研究，主要根据一些财务指标计算结合专家意见形成模型，而今，结合机器学习技术建模已成趋势。West［1］建立了基于神经网络的信用评估模型，指出多专家模型和径向基函数神经网络模型有更好的表现。肖文兵等［2］使用SVM（support vector machine）进行个人信用评估，取得了较高的分类准确率。Bhattacharyya等［3］使用SVM算法、随机森林算法和逻辑回归算法对信用卡欺诈数据分类预测。邓超等［4］利用贝叶斯界定折叠法有效解决因样本有偏引起的小企业信用评分模型分类能力丧失问题，增强了对样本填补率和模型分类能力。Lessmann等［5］系统阐释了信用评估领域的研究近况，指出异质集成学习的优越性。肖斌卿等［6］提出基于模糊神经网络开展小微企业信用评级研究，以某农村商业银行小微企业信贷微观数据为样本，实证验证了模型在小微企业信用评级中可获得更高的精度。为提高模型预测精度，在特征筛选方面，学者们做了不同方面的研究。熊志斌［7］提 出 在 传 统 CFS（correlation-based feature selection）算法中引入Gebelein最大相关系数，结合支持向量机，构建了GCFS-SVM（Gebelein CFSSVM）模型，该模型可对非线性数据进行有效的特征提取，分类预测效果较好。Vlasselaer等［8］提出同时关注数据内在特征和交易关系网络特征的特征提取方法，结合逻辑回归、神经网络和随机森林建模，获取了对异常交易较好的识别效果。Dahiya等［9］将特征选择和混合Bagging（bootstrap aggregating）模型结合，使用卡方检验对非数值型数据进行特征筛选，而对于数值型数据，使用主成分分析。Chen等［10］分别将 LDA（latent dirichlet allocation）、决策树、粗糙集以及F-score方法和SVM结合构建模型，提升了单个SVM模型的性能。特征筛选通常能在数据维数大、信息冗余的情况下提升模型性能，而建模面对的数据集信息有时是不完全的，Guo等［11］详细介绍了信用风险模型中不完整信息和延迟过滤的概念。肖进等［12］根据信息完整度划分训练集，依据数据缺失程度确定特征的权重，根据权重对特征进行随机选择，充分利用了数据信息。关于算法的研究，国内外研究者们主要采用集成学习方法来提升模型性能。Kültür等［13］基于SVM、KStar、决策树、随机森林、朴素贝叶斯和贝叶斯网络等传统模型，分别使用乐观的投票策略、悲观的投票策略和权重投票策略进行集成学习，检测信用卡欺诈。Xiao等［14］提出ECSC（ensemble classification approach based on supervised clustering）策略，先将数据集进行有监督聚类，在不同数据集上训练模型，再分配权重构建集成学习模型。Ala′raj等［15］则在进行集成学习中考虑到基分类器之间的关系，相较于传统集成策略，对错误预测有一定的修正效果。

对金融机构而言，一个有效的模型需要充分考虑利润因素而不仅仅是分类准确率。Verbraken等［16］提出基于利润的分类方法，以授信预期收益作为度量模型性能的一个因素。信用问题中对于违约客户的误判代价远高于正常客户的误判代价，而通常情况下，违约客户数目又远少于正常客户。因此，信用评估问题是代价敏感的，也是类别不平衡的。对于这类问题，可从数据角度采用重采样技术改变样本分布，使其趋于类别平衡，提高模型对正样本的关注度。重采样技术包括欠采样和过采样。欠采样减少样本集中负样本的数量，而传统基于随机抽样的欠采样方式会丢失大量信息，Ng等［17］提出DSUS（diversified sensitivity undersampling）方法，使用该方法欠采样可有效保留富含信息的样本，有利于建模。将原始数据集分布的数据处理方法与集成学习结合往往可以获取不错的效果，邹权等［18］将负样本均匀分割，依次与正样本合成训练集，使用不同算法构建基分类器，最终用投票策略建立集成学习模型。与欠采样方法相反，过采样方法增加训练集中正样本的数量，其中，SMOTE（synthetic minority oversampling technique）算法被广泛应用［19］。林舒杨等［20］对负样本进行K均值聚类，提取与正样本数目相当的聚类中心，结合SMOTE算法对样本进行适度过采样，有效避免样本过度稀疏。Sun等［21］提出 DTE-SBD（decision tree ensemble based on SMOTE，bagging and differentiated sampling rates）模型，利用SMOTE算法按照不同比例对数据集进行过采样，提高了集成学习基础分类器之间的多样性。另外，不少学者直接在算法层面改进传统机器学习方法，使其可有效应对代价敏感问题。Chung等［22］结合贝叶斯决策理论，修改SVM函数方程，使其获取的决策超平面与样本分布有关，通过超平面的偏移可使模型更多地识别正类样本。Bahnsen等［23-24］提出基于最小风险贝叶斯概率计算准则的分类器，可有效降低模型误分类带来的代价。闫明松等［25］以C4.5决策树为基算法，对代价敏感决策树和多个代价敏感Boosting算法进行了系统的对比。Hulse等［26］基于Adaboost算法，提出AsymBoost算法。关于代价敏感学习中的代价，之前的研究往往单纯定义两类样本的误分代价，近些年，学者们开始关注到具体针对个体的误分代价。Bahnsen等［27］在信用评估领域提出计算与特征有关的样本依赖的代价矩阵，使用该方法可更科学地表征代价，改善代价敏感模型性能。除了误分类带来的经济意义上的代价，一些学者还考虑到模型训练的代价，在大规模数据集建模时，权衡学习时间代价、模型维护代价和误分类代价有重要意义［28］。Yang等［29］对于具有缺失值的属性，考量获取该缺失值对于整体精度的提升度和耗费代价的关系，以建立整体代价最小的模型。

当信用数据规模较小时，对于类别不平衡问题，采用欠采样会导致模型训练所用信息不足，而仅对正样本的过采样易导致过拟合。本文在之前学者研究的基础上，提出样本依赖的SXG-BMR模型，同时对正负样本进行低倍率过采样，使样本分布明晰的同时有效避免了过拟合，以集成学习为基本模型，基于样本依赖代价矩阵，利用最小贝叶斯风险决策框架在模型中引入更符合实际的代价，大大提高了模型对于正样本的识别能力，可有效提高信用评估模型的性能。

1 样本依赖代价敏感模型的数据策略

类别不平衡问题是信用评估领域普遍需要面对的问题，而由于小微企业自身的特殊性，其信用评估过程中该问题更为突出。银行往往会主观上拒绝对小微企业的信贷以防控风险，导致历史数据集的整体数据量较少；同时，银行对小微企业的借贷要求往往更为严格，导致历史数据集中的正样本数目极少，类别不平衡的程度较高。为了应对这一问题，本文采用样本依赖的代价敏感模型框架。在数据层面上，代价敏感模型训练的输入包括数据集和代价敏感矩阵集。本文对整体样本进行过采样以明晰样本分布，并依据数据特征，针对每一个样本计算其代价矩阵，以更为精确地衡量代价。

1.1 整体样本过采样

SMOTE算法是过采样方法中的经典算法，其基本思想是在样本和其邻近同类样本连线上随机插入新的同类样本［19］。在应对类别不平衡问题上，SMOTE方法多被用于生成少数类样本，以平衡数据集。但在样本集规模较小的情况下，缺少的不只是正样本的信息，负样本的分布也很难由少数数据反映，正负样本分界超平面较为模糊。若采用SMOTE算法仅仅对每个小类样本进行过采样，将会产生一定的盲目性现象，导致有些人工合成的小类样本对大类样本的泛化空间产生影响，降低分类效果［30］。另外，SMOTE方法仅对所有少数类样本进行过采样处理，未充分考虑不同样本对分类平面的重要度的差异，易导致模型对正样本的过适应，将可能使分类器出现过拟合现象［31-32］。

为此，本文提出基于SMOTE算法对整体样本进行过采样的方法，平衡了过采样引入噪声以及降采样丢失样本的矛盾。其基本思路如下：采用SMOTE算法对整个样本集进行处理，同时生成正、负样本，样本生成比例可视实际问题数据规模而定。该方法可有效应对数据集过小或数据缺失的情况，使正负样本分界面更为明显，降低模型分类的难度，避免过拟合，提高模型的准确性。对于样本集中每一个样本，以样本xi为例，找到其K个同类近邻样本zi1，zi2，…，ziK，按公式（1）随机生成新的样本：

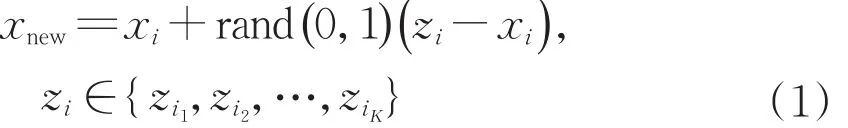
同时，根据UCI（University of California Irvine）信用数据集和上海市小微企业信用数据集的实验结果，可以发现，通过利用SMOTE算法对样本整体过采样处理得到的结果优于仅仅利用SMOTE算法对正样本进行过采样的结果，并且能够很好地实现精确率（Precision）和召回率（Recall）的平衡。

1.2 样本依赖代价矩阵

代价矩阵是标识将样本划分为不同类别所导致代价的矩阵，诸如信用评估这类二分类问题，样本xi的代价矩阵如表1所示。

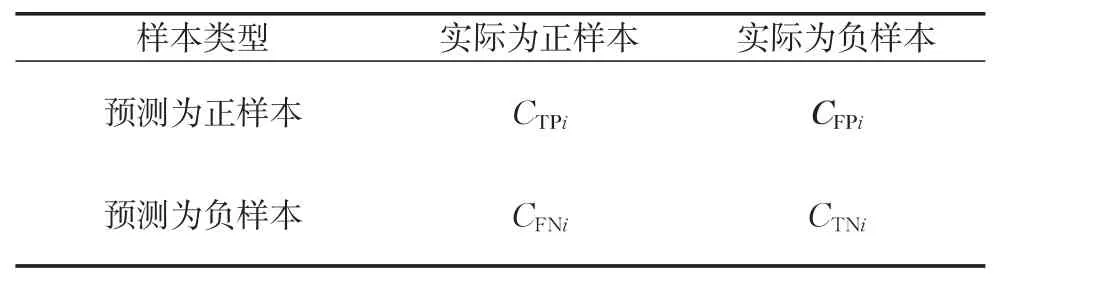
表1 样本xi的代价矩阵Tab.1 Cost matrix of sample xi

表1中，CTPi、CFPi、CFPi、CFPi分别表示样本xi不同预测结果导致的成本（代价）。关于代价敏感学习，在一些问题中，误分的代价与样本自身属性有关，而不仅仅与类别有关，比如不同贷款额度会带来不同的误分代价。Bahnsen等［27］将正确分类的代价定为0，对错误分类的代价进行计算，提出了信用评估中的样本依赖代价矩阵，如表2所示。其中，对于样本xi，Ri表示损失优质客户带来的损失，可根据借款利率和客户信用额度计算而得；CFPα基于资金不会闲置的假设，表示拒绝好的客户选择其他客户可能带来的潜在损失，可根据市场上的平均信用额度和平均利润率计算；cli表示其信用额度，可根据客户偿债能力的指标计算得到；Lgd表示坏账带来的损失占信用额度的比率，Bahnsen等在研究中拟定了Lgd为75%。通过这种规则可得出所有样本的代价矩阵，每个矩阵都是根据个体的情况计算，更精确地描述了误分类带来的代价。

表2 样本xi的样本依赖代价矩阵Tab.2 Sample-dependent cost matrix of sample xi

为了更贴近实际代价，本文根据所研究数据集所包含的特征以及市场情况，提出了相应的代价矩阵计算方法，该方法与贷款额度和样本类别比例有关，这样可以跟随样本集中两类样本的比例，调整模型对正样本的关注度，有利于提升模型的性能。对于样本xi代价矩阵中的CFPi的计算，基于资金不会闲置的假设，拒绝该客户后，将会贷给其他客户，以样本集的平均贷款额度表示将该资金贷给其他客户的额度，以样本集的平均贷款时间作为贷给其他客户的时间，以样本集的平均贷款利率作为贷给其他客户的利率，以样本中正负样本的频率分别作为贷给劣质客户和优质客户的概率。因此，本文设计样本依赖代价如下：

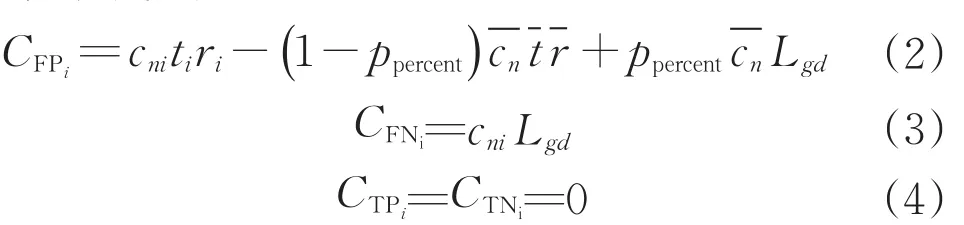
式中：cni为样本xi的贷款额度；ti为样本xi的贷款时间；ri为其贷款利率为样本集平均贷款额度为平均贷款时间为平均贷款利率；ppercent为样本集中的正样本所占比例。

2 基于样本依赖的SXG-BMR模型

鉴于 XGBoost（Extreme Gradient Boosting）算法可充分利用信息又能防止过拟合，本文构造基于最小风险贝叶斯决策的代价敏感学习框架，采用XGBoost算法，并结合前文的数据策略，提出样本依赖的SXG-BMR模型。

2.1 最小风险贝叶斯决策

若样本共有u类，分别为ω1，ω2，…，ωu，相应地，其先验概率分别为p(ω1），p(ω2），…，p(ωu）。对于样本xi，计算得到其对各类的条件概率p(xi|ω1），p(xi|ω2），…，p(xi|ωu），若已知条件概率分布类型，可使用最大似然法进行参数估计；如概率分布未知，则可用训练样本的方法进行非参数估计。根据贝叶斯公式，计算出各后验概率p(ω1|xi)，p(ω2|xi)，…，p(ωu|xi)，如式（5）所示。

进一步，引入风险代价因素，以整体风险最小化为目的优化模型，即为最小风险贝叶斯决策，应用于代价敏感学习问题，可提升模型决策性能［23］。记将属于ωj类的样本归于ωk类带来的风险为λkj。对于某个样本xi，求解式（6）得到λk*，进而得到相对应的k*，而相应的类ωk*即为样本xi的最终类别。

式中：p(ω)=(p(ω1|xi)，p(ω2|xi)，…，p(ωu|xi))；λk=(λk1，λk2，…，λku)。

2.2 XGBoost算法

XGBoost算法是梯度提升算法的一种优化实现形式，由Chen等提出并实现［33］。其目标函数包括损失函数和正则项，在进行学习迭代更新时考虑二阶导数信息，可更快地优化目标函数。同时，在目标函数中加入正则项，可控制模型复杂度，有效防止过拟合。本文应对的数据集，一方面数据规模较小，需要被充分地学习；另一方面，为提升模型对样本的识别能力，对数据集进行了一定程度的过采样，建模有过拟合的风险。在这种情况下，XGBoost是一种较为理想的算法。对XGBoost的设计如下：

对于数据集{(x1，y1)，(x2，y2)，…，(xn，yn)}，xi为样本，yi为样本xi的真实值，y^i为样本xi的预测结果，i∈{1，2，…，n}。设初始状态设为，则

第m次迭代后，

式中：y^(m)i为第m轮后对样本xi的预测结果；fm为第m轮迭代的分类器，fm∈F，F为分类器集合。

第m次迭代，XGBoost的目标函数如式（9）所示。

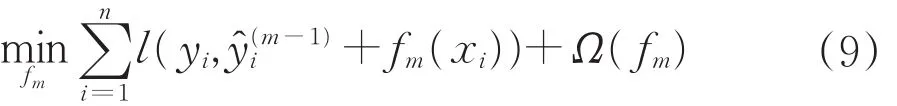
式中：l为损失函数，Ω为正则项。考虑二阶信息，对目标函数进行泰勒展开，舍去常数项，得到新的目标函数，如公式（10）所示。

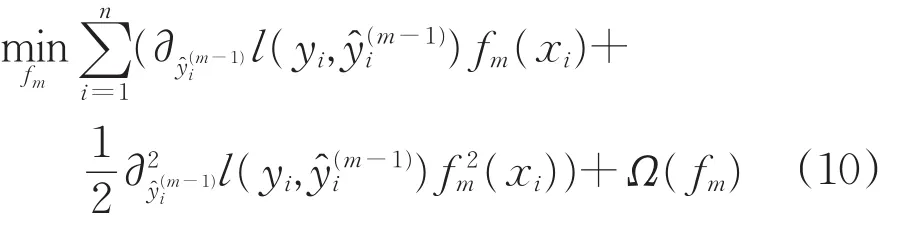
每次迭代求解得到fm，迭代M次之后，获取最终分类器y^(M)，如公式（11）所示。

2.3 样本依赖的SXG-BMR算法流程

本文基于XGBoost算法，结合数据过采样的预处理方式，利用样本依赖代价矩阵和最小风险贝叶斯决策，将代价敏感元素引入模型，从而构建了样本依赖的SXG-BMR模型。以0表征负样本（正常客户）类别，1表示正样本（违约客户）类别，具体决策流程如下：

（1）利用SMOTE算法对训练集进行整体过采样，得到新的样本集合，过采样比例根据样本规模而定。

（2）对于样本集合中每一个样本xi，计算其样本依赖代价矩阵(CFPi，CFNi，0，0)。

（3）利用XGBoost算法训练模型，得出将样本xi的预测为负类的概率

（4）获取样本xi的样本依赖代价矩阵(CFPi，CFNi，0，0)。

（5）计算对样本xi的分类预测平均代价：

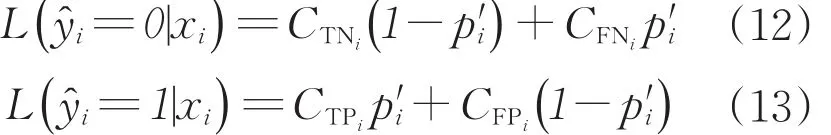
依据最小风险贝叶斯准则进行决策，将样本xi判定为预测代价小的类别。

值得说明的是，本文较为简单直接地根据客户信用额度、借贷时间两个属性进行样本依赖代价矩阵的计算，该方法具有较好的普适性。当然，代价矩阵也可由数据集给出，也可根据样本比例自行定义，两类样本比例差别越大，对正样本赋予的关注度越高，代价矩阵中CFN的值应越大。在实际操作中，如果无法获取代价矩阵，可通过不断调整参数，选出在数据集上表现最好的代价矩阵建立模型。如果不考虑代价矩阵，则模型相当于加入了SMOTE对整个样本处理的贝叶斯最小错误率决策，对于增强小样本集的模型分类性能也有一定的参考价值。

3 实验分析

本文使用了两个数据集对提出的算法框架进行验证。首先在UCI标准数据集上进行纵向、横向对比，以验证样本依赖的SXG-BMR模型的性能。在对分类算法进行对比分析时，本文选用了较为经典的Adaboost、Gradient Boosting、神经网络、决策树、随机森林、逻辑回归方法，再分别对其进行最小风险贝叶斯决策的改进，以引入代价敏感学习算法，另外还选用了代价敏感决策树和代价敏感随机森林算法作为对比对象。数据处理层面，本文进行了仅用SMOTE算法对正样本进行过采样平衡数据和对整体数据进行过采样的对比。对整体样本的过采样，不改变原始正负样本比例，为防止过拟合，对整体样本采用了较低的过采样倍数。代价矩阵层面，进行了类别依赖矩阵和样本依赖代价矩阵的对比。之后，本文将基于样本依赖的SXG-BMR模型应用于上海市小微企业信用数据集中，通过对比实验，进一步验证了该模型的有效性。本文模型性能皆使用五折交叉验证结果度量。

3.1 数据集

UCI信用数据集由Hofmann教授提供，共包含1 000个样本，有20个属性，样本分布比例如表3所示。数据集描述了客户的信用额度、贷款期限、借贷历史、借款目的、年龄、房产、工作、婚姻状况、国籍等信息，并提供了类别依赖的代价矩阵，如表4所示。

表3 UCI信用数据样本分布情况Tab.3 Sample distribution of UCI credit data

表4 信用数据代价矩阵Tab.4 Cost matrix of credit data

上海市小微企业信用数据记录了上海地区部分小微企业的历史借款违约情况，原始数据有财务型属性也有非财务型属性，考虑到小微企业财务数据的真实性问题，数据中更侧重于非财务型属性，从企业的员工情况、组成结构、历史行为等方面描述企业特征。属性主要包括企业借贷金额、企业固定资产、大股东学历、房产、车产、婚姻情况、高管学历以及信用逾期情况、法人代表学历信用逾期情况、员工学历分布、企业缴纳社保情况。共4 193条样本，样本分布情况如表5所示，样本类别不平衡程度较严重。

表5 上海市小微企业信用数据样本分布情况Tab.5 Sample distribution of credit data of smalland micro enterprises in Shanghai

3.2 模型性能度量指标

在信用评估领域，一个优质的模型应在尽可能识别有风险客户的同时避免流失优质客户，提高整体节约的代价。本文采用召回率（Recall）、精确率（Precision）、AUC（Area Under Curve，ROC曲线下的面积）和代价节省率Saving rate来度量模型性能。Recall和Precision定义如下：

式中：TP为实际正类，预测正类；FN为实际负类，预测正类。

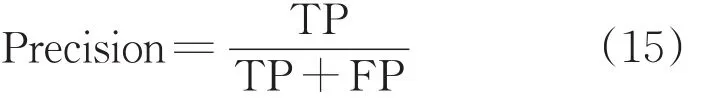
式中：FP为实际负类，预测正类。

代价节省率标识模型可度量节约代价的程度，本文将模型预测所产生的代价与将全部样本预测为正或者负产生代价中较小值相比，来表征代价节省率。对于样本集yi∈ {0，1}，i∈ {0，1，…，n}，使用分类器f(x)对T中样本进行预测，得到预测类别集合{y^1，y^2，…，y^n}，其代价节省率计算如式（16）所示。

式中：Cost(f(T))表示按照分类器的预测结果所产生的代价。

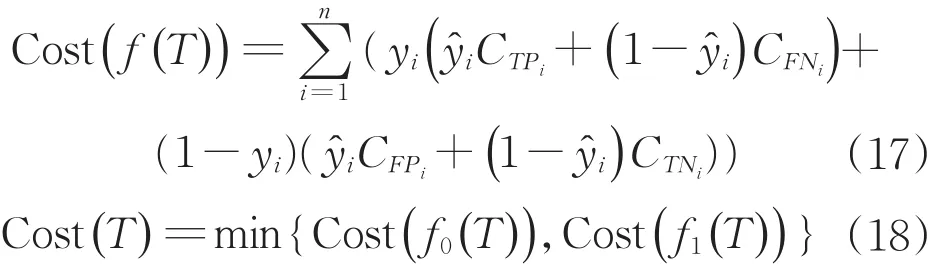
这里，Cost(f0(T))表示将所有样本全部判定为负类所带来的代价，Cost(f1(T))表示将所有样本全部判定为正类所带来的代价。

3.3 整体性能评估与比较

3.3.1 UCI信用数据集的实验结果

本文进行了不对数据集采样处理、对正样本进行过采样和对整个样本集进行不同倍率过采样的对比，以验证用SMOTE算法对样本整体过采样的有效性。所使用训练集的分布如表6所示。

表6 实验所用训练集分布情况（UCI）Tab.6 Distribution of training sets used in experiments（UCI）

根据原始数据集中提供的代价矩阵，各分类器对于初始数据集的分类结果如表7所示。选用算法包括：AB（adaboost）、GB（gradient boosting）、XG（XGBoost）、LR（logistic regression）、NN（neural network），RF（random forest）、DT（decision tree）、BMR（对模型引入Bayes minimum risk）、CS-DT（cost sensitive decision tree）和CS-RF（cost sensitive random forest）。

由表7可以看出，在未引入代价敏感元素的分类器中，各分类器效果表现均不佳，且代价节省率多为负值。在引入最小风险贝叶斯决策之后，各分类器的代价节省率有所提升，但其整体表现依然并不够理想，其Saving rate值均小于0.2。虽然各分类器的Recall值明显增大，均接近1，但是，引入最小风险贝叶斯决策之后的各分类器的Precision值比未引入代价敏感元素均偏小。这是因为该数据集的正负误分类代价比统一为1：5，而总体样本数目较少，模型无法准确得到正负样本的分布规律，导致各模型对负样本过于敏感。所以，在引入最小风险贝叶斯决策之后，各分类器的Recall值明显增大，但Precision值显著减小，AUC值也有所下降。

本文以市场一年期贷款利率为4.75%，默认坏账损失金额率为75%，计算样本依赖代价矩阵。引入样本依赖代价矩阵后，各代价敏感模型性能如表8所示，结果显示其性能优于未引入代价敏感元素的原始模型，也优于基于类别依赖矩阵的代价敏感模型，取得了Precision和Recall的平衡，提升了AUC以及代价节省率。其中XG-BMR模型表现相对较好，各性能度量指标数值较为均衡，且都优于其他模型，代价节省率高达0.434。

表7 原始数据集上各模型性能表现（UCI）Tab.7 Performance of models on original data sets（UCI）

表8 样本依赖的代价敏感模型性能表现（UCI）Tab.8 Performance of sample-dependent cost sensitive models（UCI）

选取性能表现相对较好的模型AB-BMR、GBBMR、XG-BMR、LR-BMR、RF-BMR、CS-DT和CS-RF，采用本文SMOTE方法处理数据集后，各模型在各数据集上的性能表现如表9所示。

从表9可以看出，利用SMOTE算法对样本整体过采样得到的结果优于利用SMOTE算法仅仅对正样本进行过采样得到的结果，使用SMOTE对整体数据集进行处理可以使各模型分类性能得到显著提升。对整体数据集仅扩充一倍时，使用XG-BMR模型的 Recall达到 0.771，Precision为 0.751，AUC为0.757，优于传统平衡数据集上训练模型的效果，由于样本个体代价差异，代价节省率稍弱于仅对正样本过采样的结果，但也已十分接近，这表明了对整体数据集过采样的有效性。不过，高倍过采样比例对模型性能代价提升效果有限，并未呈现明显与过采样比例正相关的关系，为了避免过拟合，对整体样本过采样程度以不超过4倍为宜。在这种情况下，基于三种Boosting算法的模型性能表现相对稳健，很好实现了Precision和Recall的平衡。其中，ABBMR模型在对整体样本过采样至四倍的数据集中获得较优效果，GB-BMR对整体过采样至三倍的数据集中获得较优效果，而XG-BMR在对整体过采样至两倍的数据集中即获取优于其余模型的表现。

因此，本实验验证了本文所提出的SXG-BMR模型的有效性，以及样本依赖代价敏感数据策略对模型性能的提升作用。

3.3.2 上海市小微企业信用数据集的实验结果

对于上海市小微企业数据集（SH），本部分实验所用的数据集分别为原始数据集、使用SMOTE平衡数据集以及对整体数据样本过采样2～4倍的数据集，具体训练集分布如表10所示。

代入市场贷款利率，计算出样本依赖代价矩阵。对于缺失借贷时间的样本，均默认为1年。各样本依赖代价敏感模型在原始数据集中的结果如表11所示。

由表11可以发现，各模型没有达到Recall和Precision很好的平衡。其中，AB-BMR、GB-BMR、XG-BMR和LR-BMR取得了较高的Recall，但Precision皆较低。而CS-RF取得了很高的Precision，为0.883，Recall却仅有0.486。

选取在原始数据集中表现相对较好的ABBMR、GB-BMR、XG-BMR、LR-BMR、RF-BMR，采用SMOTE方法处理数据集后，各模型在各数据集上的性能表现如表12所示。

由表12可知，使用SMOTE方法仅对正样本过采样平衡数据集后，模型获得了很高的Precision，但并没有很好地识别正样本，Recall相较于原始数据集大幅降低，有过拟合的倾向。而对整体样本低倍率过采样取得了较为均衡的效果，当数据集扩充至4倍时，XG-BMR模型Recall达0.937，Precision达0.713，AUC高达0.820，代价节省率为0.704，效果优于其他模型。同UCI信用数据集的实验结果类似，利用SMOTE算法对样本整体过采样得到的结果优于利用SMOTE算法仅仅对正样本进行过采样得到的结果，并且能够很好地实现各模型Precision和Recall的平衡。

本实验进一步验证了样本依赖SXG-BMR模型可有效应对类别不平衡的信用数据，高效而精确地识别违约客户，具有较好的实际应用价值。为防止过拟合，实验中对整体数据集过采样倍数控制在4倍以内，在实际应用中，也可根据实际情况适度调整过采样倍数，以获取更优的效果。

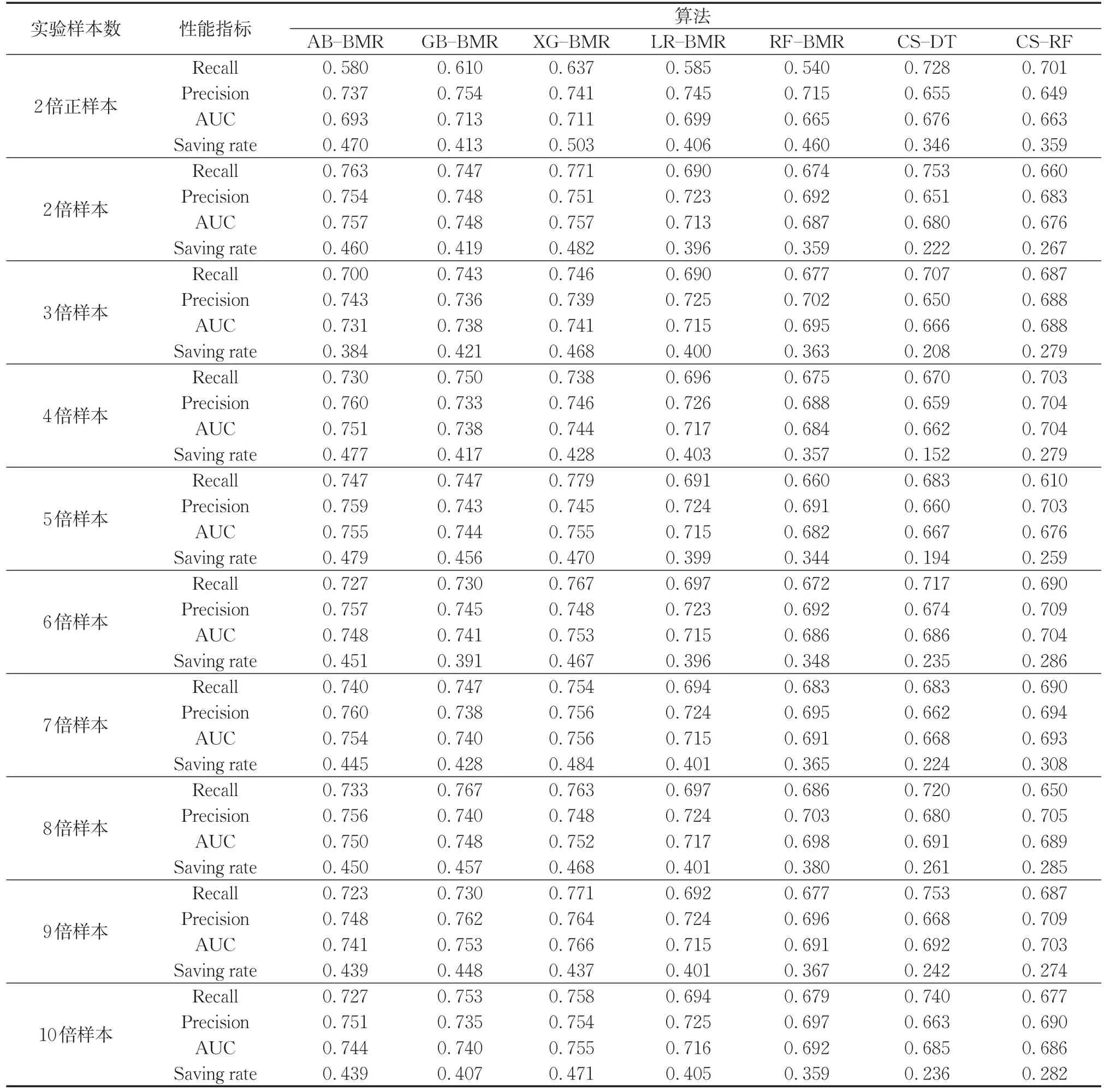
表9 样本依赖的代价敏感模型在过采样数据集的性能表现（UCI）Tab.9 Performance of sample-dependent cost sensitive model on oversampled data sets（UCI）

表10 实验所用训练集分布情况（SH）Tab.10 Distribution of training sets used in experiments（SH）

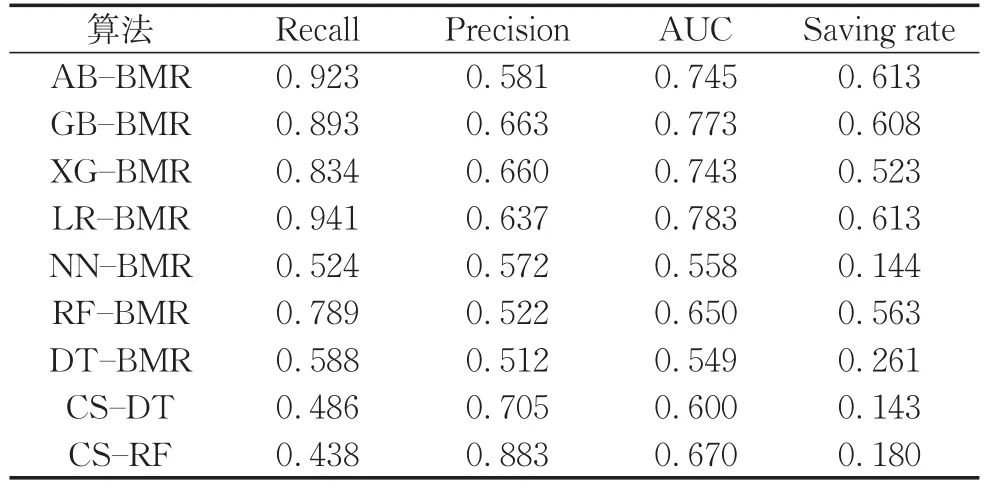
表11 样本依赖的代价敏感模型性能表现（SH）Tab.11 Performance of sample-dependent cost sensitive models（SH）

表12 样本依赖的代价敏感模型在过采样数据集的性能表现（SH）Tab.12 Performance of sample-dependent cost sensitive model on the oversampled data sets（SH）

4 结语

本文着眼于诸如小微企业这类数据集规模较小且类别不平衡的信用评估问题，改进传统的机器学习算法框架进行代价敏感学习。数据处理上，为了缓解样本中的噪声信息以及过拟合问题，本文应用SMOTE算法对整体数据集进行适度过采样，可在不产生过拟合的前提下令数据集的分布更明显。为了使模型对代价敏感，本文使用了最小风险贝叶斯决策与基本分类器结合的框架，该框架下的模型训练高效且性能较为稳健。在算法层面，构建了以集成学习算法为基础的模型，采用XGBoost集成学习算法，通过实验对比验证了其优越性。另外，本文提出了一种适用小微企业的样本依赖代价矩阵的构建方法，可应用于记录了借贷额度属性的信用数据集中。在实验中对比了类别依赖代价矩阵和样本依赖代价矩阵，验证了后者对代价敏感学习模型的性能具有显著提升作用。最后，本文提出样本依赖的SXG-BMR模型，可为金融机构针对小微企业的信用评估提供参考。

未来研究可考虑结合特征筛选，使用相较于SMOTE算法更先进的算法合成数据。另外，可引入诸如收入、资产、关系网、借贷用途等更多特征，研究更为精准科学的信用评估领域的样本依赖代价矩阵计算方法。总之，在互联网技术飞速发展的今天，金融机构的风险防控、业务经营决策将越来越依赖于大数据和人工智能，科学的信用评估体系可以帮助金融机构高效准确地识别客户类别，从而使优质企业获取资金支持，促进经济的良性发展。