心墙沥青混凝土压实PFC模拟细观参数反演

刘东海,赵梦麒

(天津大学水利工程仿真与安全国家重点实验室,天津 300350)

振动碾压是沥青混凝土心墙施工中的关键工序,对沥青混凝土结构的形成至关重要,直接关系到整个工程的进度和质量[1-2]。使用数值模拟方法来研究沥青混凝土心墙振动压实的宏-细观机理,可针对现场施工多变情况,合理地调整碾压施工参数,可重复性强、成本低。

离散元法是一种专门用于研究颗粒材料力学行为的数值模拟工具,适用于模拟具有散粒体特性的沥青混凝土心墙。国内外多利用颗粒流程序(particle flow code,PFC)研究沥青混凝土材料细观骨架结构及成型后试件的宏观物理力学性能[3-4]。

在离散元模拟过程中,材料的宏观力学行为是通过每一个接触的简单本构模型来实现的,接触模型和模型细观参数的选择尤为重要。因此,不少学者为了找到一种简单、有效的参数标定方法而展开了研究:Yoon[5]引入了最优化方法,利用数学模型和优化算法,实现了宏-细观参数的自动标定;Tawadrous等[6]和Zhou等[7]运用人工神经网络算法实现了三维模型的宏-细观参数标定;Wang等[8]利用Python语言和PFC,编写了基于模拟退火算法的参数标定程序;Belheine等[9]建立了砂土三轴压缩试验细观颗粒流滚阻模型,标定了滚阻模型细观参数。

上述研究为离散元模型细观参数的标定提供了思路,但均只适用于试件单轴压缩模拟过程中的参数标定,由于新拌沥青混凝土试件无法成型进行单轴压缩,故无法用于心墙沥青混凝土的PFC碾压模型。此外, Micaelo等[10]人对新拌沥青混合料145℃情况下的PFC2D细观参数进行了试算标定,证明了Burger’s模型在新拌沥青混合料中的适用性,但未考虑不同温度下新拌混合料细观参数的差别。因此,本文构建了适用于新拌沥青混凝土静压试验的离散元模型,针对此模型,提出了采用支持向量机(support vector machine,SVM)模型和自适应差分进化算法(adaptive differential evolution algorithm,ADE)相结合的细观参数反演方法,以期为沥青混凝土离散元模型的建立与参数标定提供依据。

1 基于SVM模型和ADE算法的模型细观参数反演方法

1.1 基本思路

图1 沥青混合料PFC模拟细观参数反演流程Fig.1 Inversion process of meso-structural parameters in PFC model for the asphalt mixture

反演离散元模型细观参数的原则是:调整细观参数使模型模拟的宏观现象与物理试验宏观现象相匹配[4]。为反演不同温度下新拌沥青混合料的细观参数,进行了PFC模型静压试验,通过匹配物理静压试验和PFC模拟静压试验的沉降量,确定模型细观参数。另外,传统试算法需要对标定参数进行不断微调试算。若采用PFC模型进行模拟试算,不仅繁琐耗时,而且通过试算很难得到全局最优参数。差分进化算法[11]是一种全局优化算法,具有结构简单、快速收敛、鲁棒性强等特点,适用于多变量函数优化问题,因此本文引入自适应差分进化算法(ADE)[12-13]对不同温度的沥青混合料细观参数进行反演。同时,为了节省PFC的计算耗时,提高反演效率,采用SVM回归模型建立待标定的细观参数与静压力-沉降量之间的关系,来替代ADE优化过程中的PFC模拟计算。反演过程如图1所示。

1.2 新拌沥青混合料静压试验PFC建模

1.2.1 基于坝料级配的静压试验PFC模型的建立

图2 沥青混合料静压试验PFC模型Fig.2 PFC model for the static pressure test of asphalt mixture

沥青混合料由粗骨料、沥青砂浆和空隙3种不同的介质组成。为考虑不规则骨料形状对混合料性能的影响,引入5种不规则形状的clump颗粒等体积替换粗骨料颗粒[14];另外,细骨料和沥青混合在一起作为沥青砂浆包裹在粗骨料表面。静圧试验模型尺寸为10 cm×10 cm×10 cm,按照真实级配生成粗骨料,并以不规则颗粒替换粗骨料圆球颗粒,为控制颗粒总数量,保证计算效率,小于2.36 mm的细骨料和沥青以2 mm的圆球颗粒作为砂浆替代[15]。为达到物理试验的坝料松铺状态,在骨料生成并替换不规则骨料完成后进行重力沉降,并去除距底部10 cm以上的颗粒。最后,导入立方体clump作为加压块,对加压块施加不同静压力,检测加压块z轴方向的位移,记为沉降量。PFC静压试验模型见图2。

1.2.2 细观接触模型

为体现沥青砂浆的黏弹性特征,表征沥青混合料的流变性能,砂浆与砂浆之间赋Burger’s模型、砂浆与粗骨料之间赋Burger’s模型、粗骨料与粗骨料之间赋线性接触模型、砂浆与墙体间赋线性接触模型、粗骨料与墙体间赋线性接触模型。接触模型的选择见图3(a),其中线性接触模型的参数不随沥青混合料温度变化,取值见文献[3-4]。因此本文主要进行Burger’s模型参数的反演。

图3 颗粒间的接触模型Fig.3 Contact models between particles

采用Burger’s模型模拟颗粒黏弹性接触时,颗粒之间接触处的法向和切向Burger’s模型如图3(b)所示。为在不影响反演结果的前提下减少待反演参数的个数,设法向参数和切向参数相同。其中,摩擦系数fn(fs)根据文献[3-4],取0.5。因此,待反演的参数为4个,分别为Maxwell模型刚度Kmn(Kms)、Maxwell模型黏度Cmn(Cms)、Kelvin模型刚度Kkn(Kks)、Kelvin模型黏度Ckn(Cks)。

1.3 SVM模型建立

1.4 细观参数反演的ADE算法设计

根据1.2.2节,本文待反演参数为4个,即ADE算法维度为4,每个个体代表一组反演参数。设当前种群数为Np,最大迭代次数为G,交叉概率为CR,缩放因子为Fp。具体步骤如下:

a. 编码与初始化。第t代的第p个参数组合为

(1)

式中:t——迭代代数,t=1, 2,…,tmax;p——参数组合,p=1, 2,…,Np。

(2)

(3)

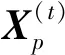
(4)

(5)

式中:drand——随机正整数,避免与父代各维分量完全相同;R3、R4、R5——[0, 1]之间的随机数;ρ2——CRp的调节概率。

d. 建立适应度函数并进行选择。将待标定温度的3种不同静压力下物理试验得到的真实沉降量分别记为s1、s2、s3;将变异差分得到的参数组合代入第1.3节建立的SVM回归模型中,得到的计算沉降量记为y1、y2、y3。为得到同时满足3种静压力下的最优参数,将3组静压力下的模拟沉降与真实沉降差的绝对值之和最小作为目标函数,即

(6)

适应值函数为

(7)

依据式(8)进行选择操作:

(8)

e. 迭代反演。依据不同温度下物理静压试验得到的沉降组合,重复进行步骤(a)～(e),直至达到最大迭代次数G,反演结束,由此得到最优化模型参数。

表1 骨料级配

注:粒径小于0.075 mm的颗粒通过率为13.0%。

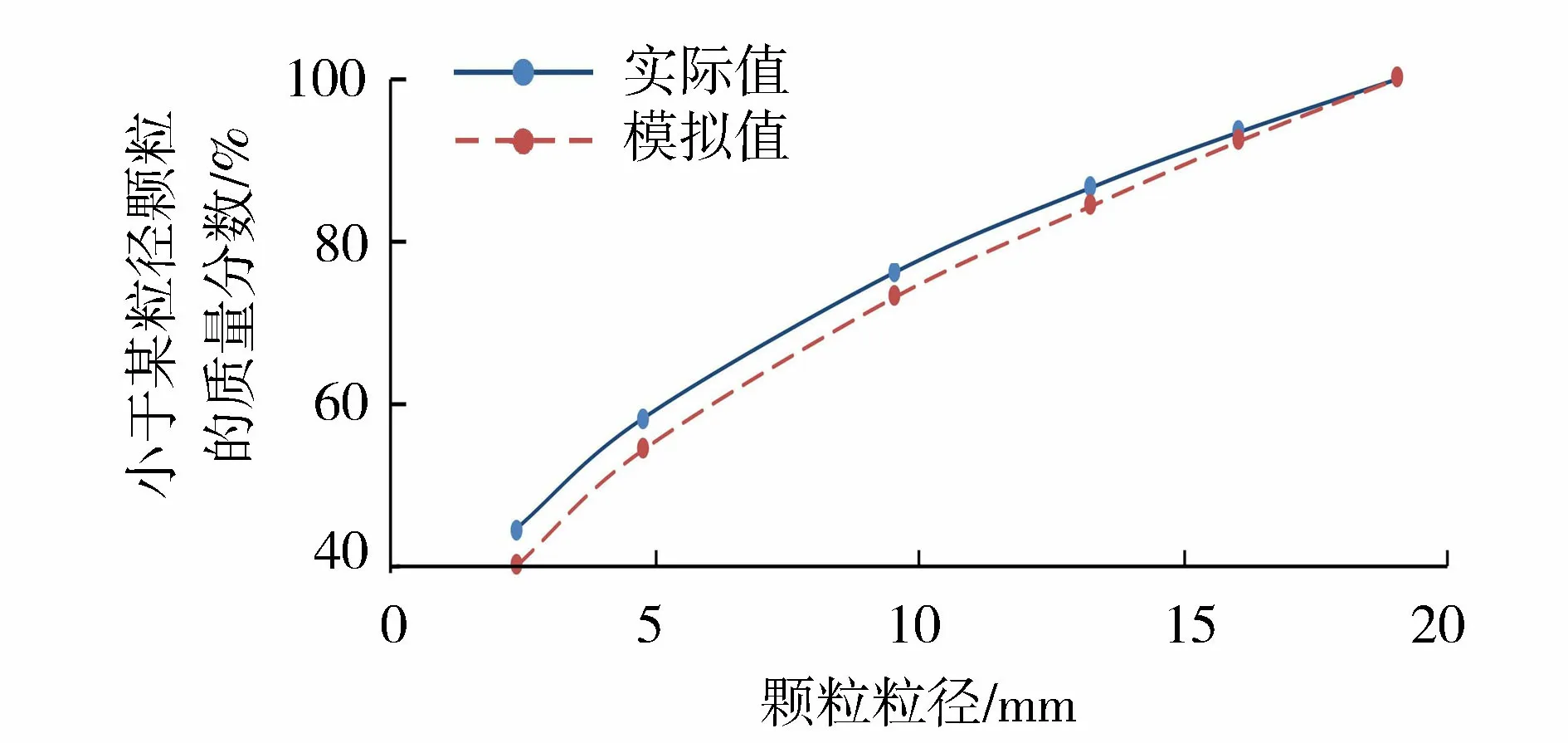
图4 实际与模拟粗骨料级配曲线对比Fig.4 Comparison of compaction settlements between the physical test and the PFC simulation

2 实 例 分 析

2.1 不同温度沥青混合料静压物理试验

为匹配物理静压试验和PFC模型静压试验的沉降量,进行了不同温度、不同静压力下的物理静压试验。

2.1.1 试验材料

试验粗骨料采用石灰岩(粒径2.36～19 mm),细骨料采用石灰岩(粒径2.36～0.075 mm),填料采用矿粉,沥青采用水工2号沥青。严格按照水工沥青混合料配合比进行骨料筛分[19],级配指数为0.41,填料质量分数为13%,油石比为7%。试验颗粒级配见表1,根据1.2.1节的方法生成各级配颗粒,模拟与实际粗骨料级配曲线对比如图4所示,粗骨料级配匹配度较高。

2.1.2 试验方法及结果

根据《水工碾压式沥青混凝土施工规范》[20],沥青混凝土心墙本体的碾压温度在120～160℃,选取145℃作为待反演温度;沥青混凝土心墙层间结合处下层温度不低于70℃,选取80℃作为第二个待反演温度;选取110℃作为第三个待反演温度(作为对照)。

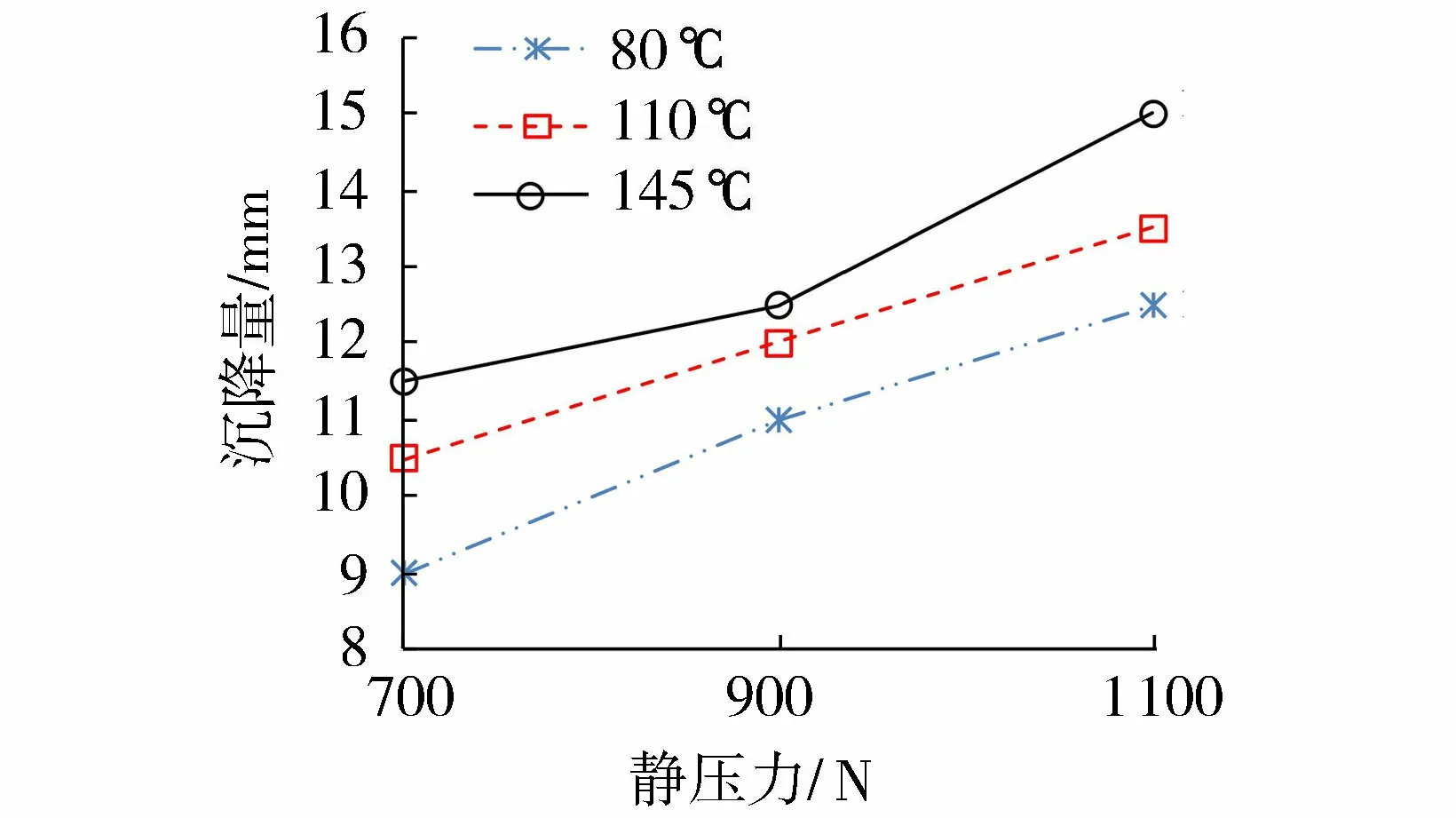
图5 不同温度下静压试验沉降量曲线Fig.5 Settlements of the static pressure tests under different temperatures

选择在3种静压力下分别进行静压物理试验,取3组沉降均满足要求的细观参数作为最终反演结果。静压力取值参照沥青心墙碾压机静压荷载,以BW 90 AD-5碾压机为例,静线荷载为890 kg/m,碾轮接地尺寸与混合料厚度、碾压机吨位和行进速度有关,一般在5～10 cm,本文取10 cm。试验试模尺寸为10 cm×10 cm×10 cm,经计算,标准静压力定为900 N。为体现组间沉降差异性并符合碾压机吨位要求,选取700 N、900 N、1 100 N静压力进行试验。试验过程将新拌心墙沥青混合料以松铺状态置于试模中,施加静压荷载至沉降量不再发生变化,记录沉降量。静压试验结果见图5。

2.2 SVM模型建立

待标定的4个细观参数为Kmn、Cmn、Kkn、Ckn,根据1.3节的方法,采用交叉分组的方式分别构建3种静压下的细观参数样本各81组,共243组。将各组参数代入PFC中进行模拟静压试验,得到对应的沉降量,根据不同静压力下各自的81组细观参数-模拟沉降量关系,分别构建不同静压力下的SVM模型,各静压力下对应细观参数的PFC计算结果与SVM模型计算结果对比,见图6。沉降量相关系数R2均在0.98以上,误差如图7所示,最大误差值不超过8%。模拟结果表明所建的SVM回归模型可以较好地计算不同参数组合下PFC模拟的沉降量。

图6 SVM模型计算沉降量与PFC模拟结果对比Fig.6 Comparison between the SVM-modeled settlement and the PFC simulated settlement

2.3 反演结果分析

设置种群数量Np=100、反演最大迭代次数G=600,参考文献[12]设初始交叉概率CR0=0.1、初始缩放因子F0=0.9。根据1.4节中得到的每种温度下的静压力-沉降值,各温度下目标函数值收敛过程如图8所示,它们均在300代左右达到收敛。

图7 SVM模型计算误差Fig.7 Calculation error of the SVM model

图8 不同温度下目标函数值收敛过程Fig.8 Convergence processes of the objective function values at different temperatures

在相同温度下,经10次反演所得结果均值、标准差及变异系数见表2。相同温度下各参数之间的差异较小,说明用自适应差分进化算法反演的细观参数具有较高鲁棒性;不同温度下,反演所得各参数均值之间差异明显,且随着温度降低,Kmn、Kkn、Cmn、Ckn都呈增大趋势,符合随温度降低新拌沥青混合料黏度、刚度增大的客观规律。

表2 反演10次结果统计

表3 不同温度下的细观参数反演结果

选取10组参数组合中累计相对误差最小的1组作为最优的反演参数,见表3。将该参数取值代入所建立的PFC中,模拟计算新拌沥青混合料的静压沉降量,各工况下模拟沉降曲线如图9所示。模拟结果与物理试验结果对比如表4所示。两者相对误差较小,可见本文所提出的方法得到的模型细观参数合理。

图9 不同工况下的PFC模拟沉降曲线Fig.9 PFC simulated settlement curves under different conditions

表4 物理试验与PFC模拟计算的压实沉降量比较

3 结 语

为了获取不同温度下心墙沥青混凝土的PFC模型细观参数,在不同温度下对沥青混合料进行不同静压力的静压试验,同时建立了沥青混合料静压试验PFC模型,并建立待反演细观参数与模拟沉降量的SVM回归模型,结合自适应差分进化算法对不同温度下新拌沥青混合料的细观接触参数进行反演。研究结果表明:本文提出的通过静压力-沉降量关系,结合SVM回归模型和自适应差分进化算法,可以对不同温度下新拌沥青混合料的细观参数进行反演,并能获取合理的PFC模型细观参数,使得模型计算的沉降量与物理试验结果较吻合。

在本文的基础上,利用反演所得的细观参数,可以进一步对沥青混凝土心墙坝料本体与层间结合处的细观压实机理进行研究。