GRANULE 和MANTRA 算法的不可能差分区分器分析

武小年，李迎新，韦永壮，孙亚平

（1.桂林电子科技大学广西密码学与信息安全重点实验室，广西 桂林 541004；2.保密通信重点实验室，四川 成都 610041；3.广西高校云计算与复杂系统重点实验室，广西 桂林 541004）

1 引言

近年来，伴随着电子信息技术的迅速发展，射频识别、传感器网络和智能卡等微型计算设备应用需求不断增大。注意到，这些微型计算设备的存储空间小、计算能力弱、功耗小等资源受限特点使常规的对称密码算法并不适用。如何设计新型的轻量级密码算法，以满足各种资源受限环境下的使用，成为目前的研究热点。过去的10 年里，多个轻量级算法被相继提出，比如LBlock、GIFT、Midori、PRESENT、MIBS、LED、SPECK等密码算法。另一方面，轻量级分组密码的安全性至关重要，常见的密码分析方法包括差分密码分析[1]、线性密码分析[2]、不可能差分分析[3-4]、积分分析[5]等。

不可能差分分析是对差分分析的扩展，由Knudsen[3]和Biham 等[4]提出。不可能差分分析的关键在于构造不可能差分区分器，以进行密钥筛选。由于该攻击方法简单、有效，因此广泛应用到分组密码攻击中[6-8]。为了能够快速高效地寻找高轮数的不可能差分区分器，多种自动化搜索方法被先后提出。2012 年，Wu 等[9]提出一个较通用的不可能差分区分器的自动化搜索方法，其将r轮分组密码结构视为一个方程组，描述了内部基元中差分的传播行为，尤其是分组密码结构的S 盒置换或分支交换。2017 年，Luo 等[10]改进Wu 等[9]提出的自动化搜索方法，并测试该方法是否存在解，其主要简化了最耗时的矩阵运算，在更短的时间内找到了更多不可能的差分，提高了搜索效率。同年，Sasaki 等[11]针对分组密码算法，提出了基于MILP 模型的比特级的不可能差分自动化捜索方法，并给出了Midori-128 算法的7 轮不可能差分区分器。2018 年，韩亚等[12]通过学习基于比特的可分性质，利用三子集传播方程，提出一种基于SAT/SMT 求解器自动化搜索ARX 结构分组密码积分区分器的方法。张仕伟等[13]利用SIMON 中AND 组件的差分传播特性，构造2 条约束条件，结合SAT 求解器提出了自动化搜索算法，搜索出多条11 轮不可能差分区分器，该算法可以准确地判断SIMON 算法的任意差分对能否构成一条不可能差分区分器。Zhang 等[14]提出了“Modes operation”方法，用于对ARX 类型的密码算法进行不可能差分区分器的自动化搜索。

2018 年，Bansod 等提出了2 种轻量级分组密码算法——GRANULE[15]和MANTRA[16]。这2 种算法均使用了典型的Feistel 结构，并采用了轻量级S 盒和简单的位操作，使其能够在较少的轮数中完成最大扩散效果。他们对GRANULE 和MANTRA算法分别进行了安全性分析，表明2 种算法均能有效地抵抗差分分析、线性分析、Biclique 攻击、零相关分析等。2019 年，石淑英等[17]针对GRANULE算法构造了9 个5 轮不可能差分区分器，但是该方法在构造不可能差分区分器中并未考虑算法内部核心部件代数性质。如何针对这些新算法构建更高轮数的不可能差分区分器有待深入解决。

本文基于GRANULE 和MANTRA 算法结构，利用密码S 盒差分分布表新性质，结合中间相遇思想，提出了一种不可能差分区分器的新自动化搜索方法。基于该搜索方法，本文发现GRANULE/MANTRA 算法有144/52 个不同的7/9 轮的不可能差分区分器。

2 算法介绍

2.1 GRANULE 算法简介

GRANULE 算法是一种基于Feistel 结构的轻量级分组密码算法，分组长度为64 bit，支持80 bit和128 bit 这2 种密钥长度，迭代轮数为32 轮。该算法中的轮函数F包括置换层、S 盒、循环移位、密钥加和异或运算。GRANULE 算法结构如图1所示。

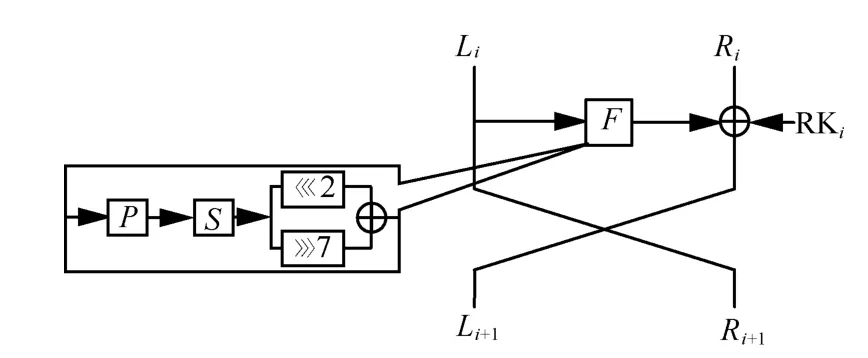
图1 GRANULE 算法结构

设GRANULE 算法第i轮输入是Ci，输出是Ci+1，该算法的左分支和右分支分别记为Li和Ri(i=0,1,2,…,31)，则从(Li,Ri)更新至(Li+1,Ri+1)，更新过程为

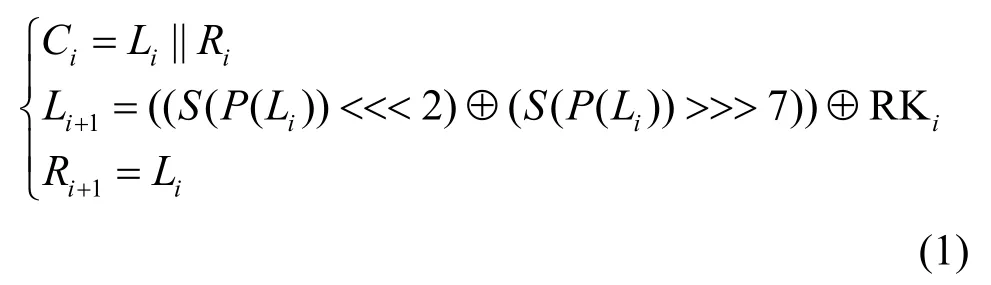
GRANULE 算法采用一个4 bit 的S 盒，即{0,1}4→{0,1}4。S 盒具体数值以十六进制的形式给出，如表1 所示。

表1 GRANULE 算法S 盒

2.2 MANTRA 算法简介

MANTRA 算法是一种基于Feistel 结构的轻量级分组密码算法，分组长度为64 bit，支持80 bit和128 bit 这2 种密钥长度，迭代轮数为32 轮。该算法中的轮函数F是由2 轮的Feistel 结构拼接而成，这2 个Feistel 结构都包含了S 盒、密钥加、循环移位和异或运算4 个基本操作。MANTRA 算法结构如图2 所示。

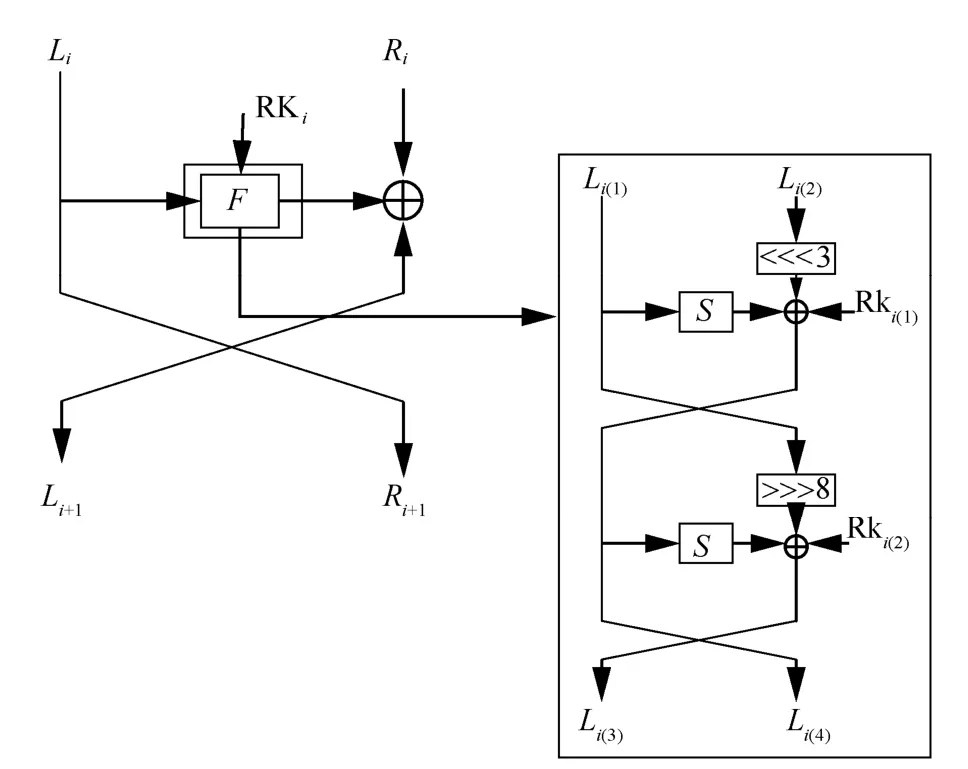
图2 MANTRA 算法结构

设MANTRA 算法的第i轮输入是Ci，输出是Ci+1，该算法的左分支和右分支分别记为Li和Ri(i=0,1,2,…,31)，则从(Li,Ri)更新至(Li+1,Ri+1)，更新过程为

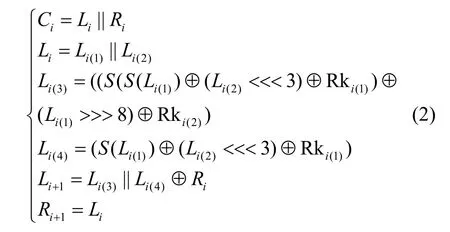
MANTRA 算法中使用的是一个4 bit 的S 盒，即{0,1}4→{0,1}4。S 盒具体数值以十六进制的形式给出，如表2 所示。

表2 MANTRA 算法S 盒

3 2 种算法的不可能差分区分器构造

2014 年，Tezcan[18]提出一种针对S 盒评估以及S 盒差分传播的新标准。当给定S 盒的差分输入值时，对应S 盒的输出差分中至少有1 bit 的概率为1，即可以确定该输出差分中的1 bit 的差分值。被确定概率为1 的比特被称为未受干扰比特。基于该思想，对密码算法中S 盒的差分分布表进行分析，通过分析输入/输出差分值，找到未受干扰比特。将该方法应用于不可能差分分析中，可获得更长的不可能差分区分器。

针对GRANULE 和MANTRA 算法的不可能差分区分器自动搜索方法，主要是通过分析2 种算法S 盒的差分分布表，得到2 种算法对应的S 盒差分特征，再利用中间相遇思想，对2 种算法分别从加/解密方向得到的差分路径进行遍历，筛选出概率为0 的最优差分路径，即不可能差分区分器。

3.1 S 盒的差分特征

Biham 等[1]对DES 算法进行差分密码分析的关键在于观察到S 盒差分分布不均匀特性，并给出了S 盒差分分布表的概念，这个概念完全刻画了S 盒的差分传播特征，实际上也是满足特定差分的随机输入对经过S 盒作用后输出差分的分布特征。基于文献[18]中使用的方法，对差分分布表输入/输出差分进行分析总结，得到S 盒的输入/输出差分特征，将该特征应用到不可能差分区分器的推导过程中，可有效提高不可能差分区分器的长度。

定义1S 盒差分分布表。设i,j∈N，给定m∈，n∈，从到的非线性映射（也称为S 盒）定义为

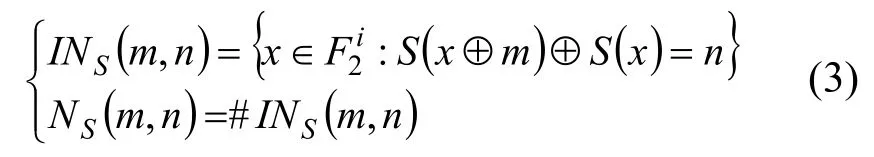
构造2i×2j的表格如下：以m为行指标遍历，n为列指标遍历，行列交错处的取值NS(m,n)。称m为S 盒的输入差分，n为S 盒的输出差分。三元数组(m,n,NS(m,n))按上述方式构成的表即为S 盒的差分分布表。

3.1.1 GRANULE 算法S 盒的差分特征

根据定义1，构造GRANULE 算法S 盒的差分分布表，GRANULE 算法S 盒的差分分布表如表3 所示。

当S 盒的输入/输出差分为某些定值时，其输入/输出差分会存在一定的规律性。如输入差分为0001时，输出差分可能为1000，1001，1010，1011，1100，1101，1110，1111。而这些输出差分的第3 比特均为1，另外3 个比特的差分未知，简记为1***（其中“*”表示未知差分）。根据该方法，对表3 进行总结可得到性质1。

性质1GRANULE 算法S 盒的差分分布表输入/输出差分不均匀的特征表明，当S 盒的输入差分为某些定值时，其输出差分存在相应的特征，其输出差分存在的传播特性如表4 所示。

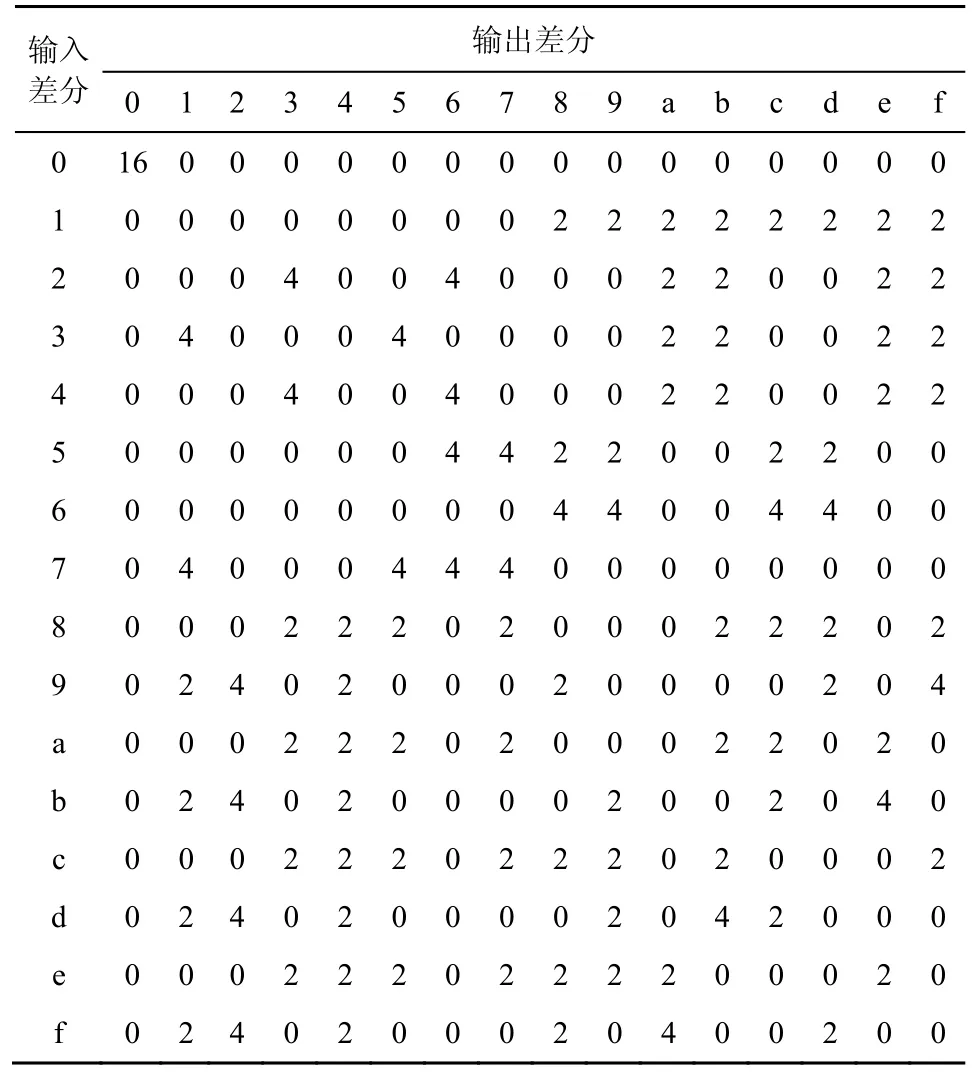
表3 GRANULE 算法S 盒的差分分布表

表4 GRANULE 算法S 盒输入/输出差分特征

表4 中，“*”表示差分未知，“0”表示差分为0，“1”表示差分为1。将表4 中GRANULE 算法S盒的差分特征应用于该算法的加/解密过程中，可有效拓展不可能差分区分器的长度。

3.1.2 MANTRA 算法S 盒的差分特征

根据定义1，构造MANTRA 算法S 盒的差分分布表，然后利用3.1.1 节中的方法对S 盒的差分分布表进行分析可得到性质2。

性质2MANTRA算法S盒的差分分布表输入/输出差分不均匀的特征表明，当S 盒的输入差分为某些定值时，其输出差分存在相应的特征，其输出差分存在的传播特性如表5 所示。

表5 MANTRA 算法S 盒的输入/输出差分特征

将表5 中MANTRA 算法S 盒的差分特征应用于该算法的加/解密过程中，可有效拓展不可能差分区分器的长度。

3.2 GRANULE 算法不可能差分区分器自动搜索方法

从GRANULE 算法S 盒差分分布表的输入/输出差分中找到S 盒的输入/输出差分传播特征，在此基础上，基于中间相遇思想，先从加密方向找到一条概率为1 的有效差分路径，然后从解密方向找到一条概率为1 的有效差分路径；再在上述的加密方向的路径集合和解密方向的路径集合中进行遍历，并将其拼接，筛选出一条概率为0 的最优差分路径，即不可能差分区分器。在搜索筛选概率为0的最优差分路径过程中，采用自动化搜索的方式进行遍历。

中间相遇思想是构造不可能差分区分器的常用方法，将一个密码算法T分成两部分：T=T0T1，T0存在概率为1 的差分ΔE→ΔF，T1存在概率为1的差分ΔG→ΔH；如果ΔF和ΔH不相等，那么对于T就存在概率为0 的差分ΔE→ΔG，即ΔE→ΔG称为“不可能差分区分器”，如图3 所示。

图3 不可能差分区分器原理

3.2.1 GRANULE 算法有效差分路径

对GRANULE 算法有效差分路径的搜索，首先是在算法的加密方向，利用中间相遇思想找到一条概率为1 的差分路径，具体地，当输入差分在经过轮函数中S 盒时，利用性质1 中S 盒的差分特征进行差分传播，输出较为准确的差分，直到输出差分全为未知差分时，则停止搜索加密方向的差分路径，并输出差分路径集合。其次，在算法的解密方向，按照同样的方式，从相反的解密方向进行搜索，最终输出解密方向的差分路径集合。

GRANULE 算法加密方向搜索概率为1 的差分路径过程如算法1 所示。

算法1GRANULE 算法加密方向有效差分路径自动搜索

输入64 bit 差分明文M，其左右分支分别记为Li和Ri(i=0,1,2,…,31)

输出输出每轮经过轮函数的输出差分集合List

3.2.2 GRANULE 算法不可能差分区分器

基于上述GRANULE 算法加/解密方向自动搜索的概率为1 的差分路径集合，利用中间相遇思想，对算法1 得到的加密方向的差分路径集合和解密方向的差分路径集合进行遍历拼接，搜索一条概率为0 的最优差分路径，即不可能差分区分器。

GRANULE 算法搜索不可能差分区分器过程如算法2 所示。

算法2GRANULE 算法不可能差分区分器自动搜索

输入加密方向差分路径集合List_en，解密方向差分路径集合List_de

输出输出最优不可能差分区分器轮数

算法2 通过遍历算法1 中得到的加密方向差分路径集合和解密方向差分路径集合，每次分别从加密方向和解密方向路径中选取一条数据，利用contradiction 函数进行矛盾点的检测。通过遍历和检测，最终输出最优不可能差分区分器轮数。

由于GRANULE 算法的分组长度为64 bit，遍历所有可能差分的复杂度太高，因此本文只对具有1 bit 活跃的输入/输出差分对进行搜索。利用上述自动搜索方法进行搜索，搜索到了144 个不同的7 轮不可能差分区分器，图4 给出了其中一条不可能差分区分器的具体形式。

表6 列出了所搜索出的GRANULE 算法部分7 轮不可能差分区分器，其中，vi(0≤i≤7)表示第ibit 的差分为1，其余比特差分为0，0 表示该字节的差分为0。

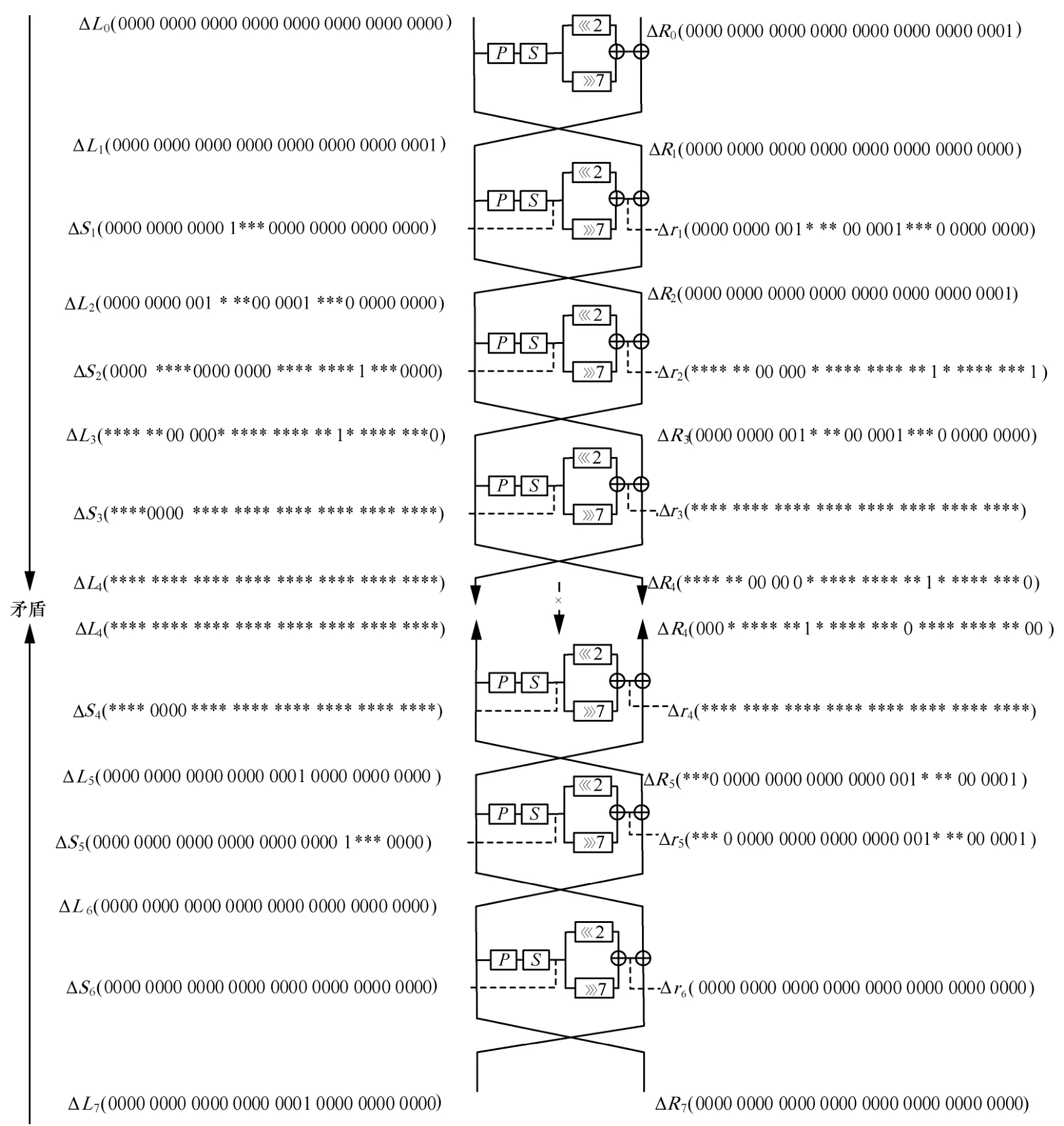
图4 GRANULE 算法不可能差分区分器示意

表6 GRANULE 算法不可能差分区分器

3.3 MANTRA 算法不可能差分区分器自动搜索方法

MANTRA 算法不可能差分区分器的搜索方法与GRANULE 算法不可能差分区分器的搜索方法类似，是根据MANTRA 算法的差分特征，再采用中间相遇思想，分别从加/解密方向各找到一条概率为1 的有效差分路径；再对加/解密方向的路径集合进行遍历和拼接，筛选出一条概率为0 的最优差分路径，即不可能差分区分器。2 种算法搜索方法不同的地方在于2 种算法S 盒的差分特征不同，因此MANTRA 算法在搜索加/解密方向的有效差分路径时，需要根据其自身算法S 盒的差分特征进行传播，从而输出对应的差分路径。

由3.2 节中提出的不可能差分区分器自动化搜索方法，利用性质2 中的MANTRA 算法S 盒的输入/输出差分特征，只对具有1 bit 活跃的输入/输出差分对进行自动化搜索，可搜索到52 个不同的9轮不可能差分区分器，表7 列出了所搜索出的MANTRA 算法部分9 轮不可能差分区分器，其中，vi(0≤i≤7)表示第ibit 的差分为1，其余比特差分为0，0 表示该字节的差分为0。

表7 MANTRA 算法不可能差分区分器

4 分析结果对比

为加强对GRANULE 算法和MANTRA 算法的安全性分析，并给出本文不可能差分区分器对这2种算法的分析结果，采用Java 语言实现了本文提出的搜索方法，并在处理器为Intel i5-8500，内存为8 GB的Windows10 家庭版系统环境下运行，算法的时间复杂度为O(n4)，其中，n表示输入的明文长度。针对GRANULE 算法和MANTRA 算法，遍历1 bit活跃的输入输出差分对，测试所使用的时间分别为392 ms 和274 ms。

为进一步归纳对这2 种算法的现有方法安全性分析结果，将本文分析结果与现有文献进行了对比。针对GRANULE 算法的安全性分析，将本文结果与文献[10,17]中提出的自动化搜索方法，以及文献[15]采用的零相关线性分析进行对比。零相关线性分析由Bogdanov 等[19]提出，该分析方法是寻找密码算法概率为，即相关性为0 的线性逼近作为零相关线性分析的区分器，进而区分出正确密钥和错误密钥。零相关线性分析作为不可能差分分析的对偶方法，存在与不可能差分区分器对比的合理性。针对MANTRA 算法的安全性分析，将本文结果与文献[10]中提出的自动化搜索方法，以及文献[16]中的零相关线性分析进行了对比。对 GRANULE 算法和MANTRA 算法的分析结果如表8 所示。

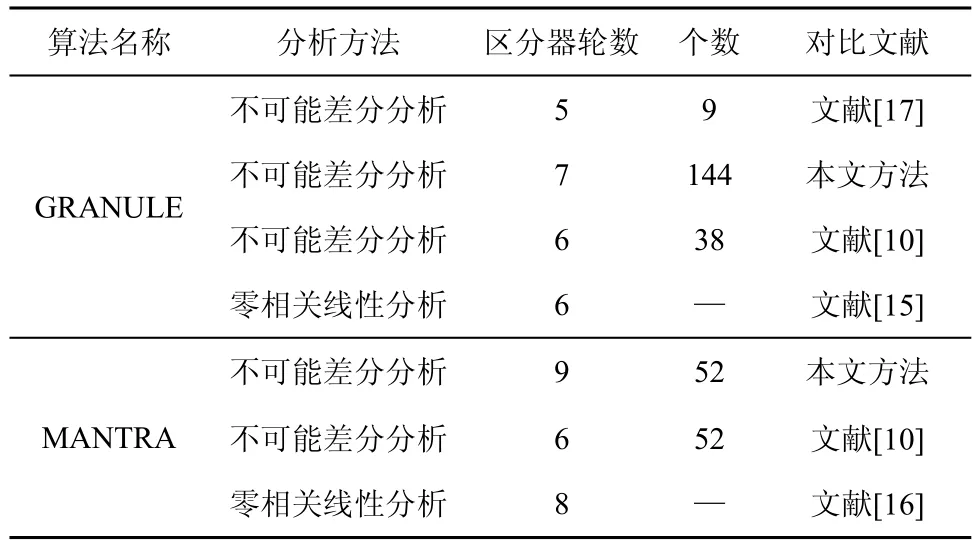
表8 对GRANULE 算法和MANTRA 算法的分析结果

文献[15]在提出GRANULE 算法时，使用零相关线性分析的分析方法对其进行安全性分析，构造出 6 轮的零相关线性区分器。文献[17]针对GRANULE 算法给出了9 条5 轮不可能差分区分器中，其S 盒的输入/输出差分仅考虑“0”与“非0”这2 种情况，即输入差分为“0”时，输出差分也为“0”；输入差分为“非0”时，输出差分为“****”。文献[10]对GRANULE 算法的自动化搜索，得到38 个6 轮不可能差分区分器，其采用线性运算，以半字节进行搜索，搜索时间为76 ms。本文通过对GRANULE 算法中S 盒的差分分布表的输入/输出差分进行总结，得到性质1 所示的S 盒差分特征，其能够获得输入/输出差分的传播规律，如在非0 情况下，若输入差分为“0001”其输出差分为“1***”；将该性质与中间相遇思想结合，采用自动化搜索方法，以比特进行搜索，搜索时间较文献[10]更长，但获得的不可能差分区分器的轮数也更长。

文献[16]在提出MANTRA 算法时，使用零相关线性分析的分析方法对其进行安全性分析，构造出8轮的零相关线性区分器。文献[10]对MANTRA 算法的自动化搜索，得到52 个6 轮不可能差分区分器，其采用线性运算，以半字节进行搜索，其搜索时间为51 ms。本文通过对MANTRA 算法S 盒的差分分布表的输入/输出差分进行总结，得到性质2 所示的S盒差分特征，通过结合中间相遇思想，并采用自动化搜索方法，以比特进行搜索，搜索时间较文献[10]更长，但获得的不可能差分区分器的轮数也更长。

综上所述，通过分析密码算法S 盒的差分分布表的输入/输出差分特征，并采用自动化搜索方法，结合中间相遇思想，可以提高算法的不可能差分区分器长度。

5 结束语

本文针对GRANULE和MANTRA算法的结构特性，通过分析其S 盒差分分布表获得对应的差分特征性质，结合中间相遇思想，采用自动化搜索的方式，在加/解密方向分别找到一条概率为1 的有效差分路径；再在上述的加/解密方向的路径集合中进行遍历，找到一条概率为0 的最优差分路径。研究结果发现，GRANULE/MANTRA 算法有144/52 个不同的7/9 轮的不可能差分区分器。在后续工作中，将充分地考虑密码核心部件的代数性质，以获得更高轮数的区分器。