认知网络干扰效率最大稳健功率与子载波分配算法

徐勇军，杨洋，刘期烈，陈前斌，林金朝

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.山东大学山东省移动通信技术重点实验室，山东 济南 250100）

1 引言

近年来，随着新一代无线通信时代的到来以及终端设备和应用数量的迅速增加，可用的频谱资源越来越少。为了充分利用频谱资源以提升系统吞吐量和用户容量，认知无线电技术[1-2]应运而生，其特点体现在能够有效提升空闲频谱利用率。凭借该技术，次用户能够感知主用户的频谱占用情况，并对空闲频谱进行再利用。对于下垫式认知网络[3-5]，为保证主用户的服务质量（QoS,quality of service），可以通过设置所有次用户发射机到每个主用户接收机的干扰温度阈值来实现。

通过正交频分多址接入（OFDMA,orthogonal frequency division multiple access）技术，可用频谱被划分为一组相互正交的子载波，且子载波可以进行灵活的分配[6]。OFDMA 技术可以很好地满足认知网络频谱资源灵活调度的特点，因此，对认知OFDMA 网络的各类研究成为学术界和工业界的关注焦点[7-8]。

目前，对认知OFDMA 网络资源分配问题的研究已经取得了很多有价值的成果。现有研究主要可以分为以下2 类：1)传输数据速率（吞吐量）最大，主要目标是使次用户网络总数据速率最大；2)能量效率最大，主要目标是使总数据速率与总功率消耗的比值最大。在数据速率最大化方面，文献[9]研究了多跳认知无线电网络的子载波和功率分配联合优化问题，针对吞吐量最大和功率最小这2 个优化目标进行对偶求解。文献[10]研究了认知OFDMA网络频谱感知和跨层调度联合设计问题，并提出了一种基于对偶分解的算法。文献[11]对认知OFDMA网络的联合信道和功率分配问题进行了研究，该研究以纳什均衡理论为基础，引入次用户的最小速率约束和比例公平性，提出了一种非迭代的最优平衡算法。以上算法都以最大化数据速率为优化目标，却忽略了系统能量消耗问题。然而，目前随着终端和物联网技术的发展，导致出现很多终端能量受限的网络，如D2D 网、无线传感器网络。因此，如何在降低系统总能量开销的前提下，保证一定传输速率，也是一个值得研究的问题。为满足绿色通信的要求，提高单位功率产生的吞吐量，文献[12-14]讨论了能量效率作为优化目标的资源分配问题。其中，文献[12]对认知小蜂窝网络中的功率控制和感知时间优化问题进行了研究，通过考虑不完美的混合频谱感知、跨层干扰约束、最小数据速率约束，以最大化能效为目标，提出了一种迭代功率控制算法和次优感知时间算法。文献[13]针对广播电视空白频谱，研究了子信道和功率分配问题，以最大化次用户的能量效率为目标，并保持对邻近区域主用户的干扰低于指定阈值，提出了一种功率和频谱分配协议。文献[14]研究了具有数据速率要求和最大功率约束，最小化所有子载波上每比特的能量消耗资源分配问题，提出了一种分布式的频谱接入和资源分配算法。

上述研究中的资源分配问题，主要考虑完美信道状态信息，优化目标集中在网络吞吐量和能效问题。然而，上述工作主要通过引入干扰温度约束来实现功率分配和资源共享，但是忽略了干扰对整个系统性能的影响。另外，传统的节能资源分配算法只能在合适的最大发射功率阈值下获得良好的性能。在实际的认知无线电系统中，干扰温度线远低于次用户发射机的发射功率阈值，这使得在优化过程中，最大发射功率约束通常失效。另一方面，由于无线通信系统固有的信道条件随机性和认知网络存在的频谱感知误差，完美的信道状态信息是难以保证的，非稳健资源分配算法应用在实际通信场景中会导致通信中断，使用户体验降低。

本文的主要贡献如下。

1)建立了基于干扰效率最大化的多用户认知OFDMA 网络资源分配模型。为有效地保证主、次用户的用户性能，引入了随机信道不确定性参数，将该模型转换成基于中断概率的稳健功率分配和子载波分配问题模型。该资源分配问题是包含整数变量和中断约束的优化问题。

2)利用伯恩斯坦近似和Q 函数性质，将稳健中断概率约束转换成为凸约束。利用Dinkelbach转换法，将原非凸分式规划问题转换为凸优化问题，提出了一种基于拉格朗日对偶分解和次梯度更新的资源分配算法，并进行了计算复杂度和灵敏度分析。

3)仿真结果显示算法具有良好的收敛性、稳健性和干扰效率。

2 系统模型与问题描述

2.1 非稳健资源分配模型

本文考虑基于OFDMA 的下垫式认知网络上行传输场景，网络中有K个次用户和M个主用户。系统总带宽为BHz，被划分成N个子载波。因此，每个子载波的带宽是。假设每个子载波只能由一个次用户使用，为获得良好的传输质量，每个次用户可以占用多个不同的子载波。假设信道服从平坦衰落模型。定义主用户的集合为∀m∈M={1,2,…,M}，子载波集合为∀n∈ N={1,2,…,N}，次用户 的集合 为∀k∈ K={1,2,…,K}。系统参数如表1 所示。

表1 系统参数描述

为保障主用户的服务质量，所有次用户对第m个主用户所产生的干扰应满足

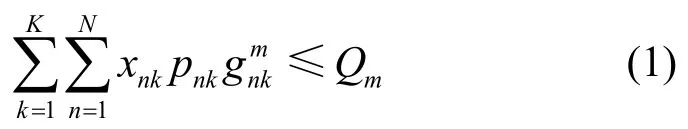
其中，xnk是子载波分配因子，xnk=1意味着第n个子载波被分配给第k个次用户，否则，xnk=0。

每个子载波只能由一个次用户使用，因此，子载波分配因子约束为

由于移动终端电池容量有限，对于每个次用户，有最大发射功率约束，即

根据香农公式，第k个次用户在第n个子载波上可实现的传输速率为

为了在有限的资源下找到理想的度量标准，本文引入干扰效率来降低对主用户接收机的干扰功率，并提高次用户的数据速率。因此，有

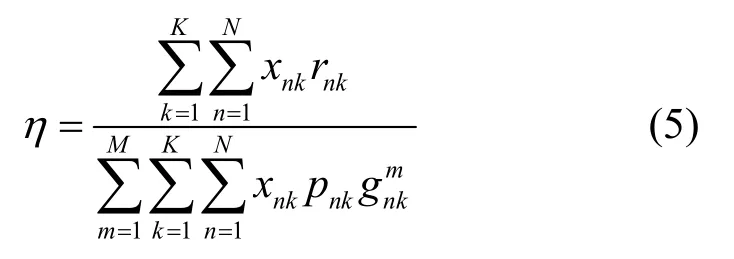
一方面，该优化目标试图尽可能地降低对主用户的干扰。另一方面，其又尽可能地提升次用户的总数据速率。因此，基于干扰效率的最大化资源分配问题可表示为

其中，约束条件C1 和C2 可以确定次用户发射功率可行域的上限，前者用于保障每个主用户的服务质量，后者用于限制每个次用户发射机的最大发射功率；C3 保证每个子载波只能分配给一个次用户；C4 用于保障每个次用户的服务质量。

2.2 稳健资源分配模型

在实际的认知网络中，由于存在信道估计误差和频谱感知误差，要获得完美信道状态信息是很困难的。信道不确定性可以表示为不确定参数的加性模型[3]，即

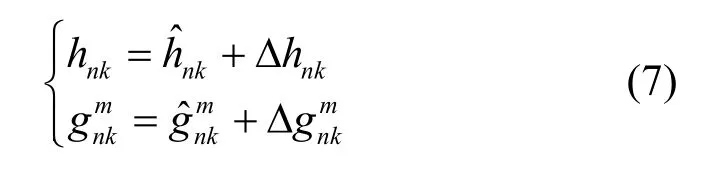
其中，是次用户到其基站的传输链路估计信道增益，是次用户发射机到主用户接收机的干扰链路估计信道增益，这些参数对次用户来说是已知的；是对应的摄动项，即信道估计误差。

基于式(7)中信道增益的不确定性形式，考虑用户的中断概率约束，可将问题(6)重新表述为

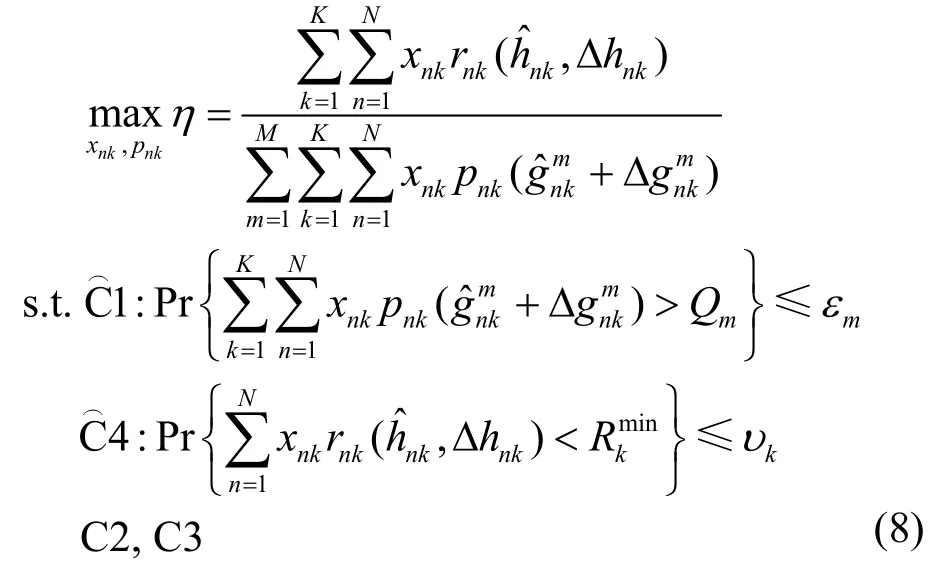
其中，εm和υk分别表示第m个主用户和第k个次用户的中断概率门限，这保证在恶劣的信道环境中，主用户和次用户的服务质量不会受到严重影响。显然，由于问题(8)的目标函数是非凸的，问题中包含整型变量且存在中断概率形式的约束条件，要直接求得该问题的解析解是很困难的。

3 稳健优化问题转换

鉴于稳健资源分配问题(8)难以求解，本节首先利用伯恩斯坦近似法对干扰中断概率约束进行凸转换，再根据Q 函数性质对数据速率中断概率约束进行凸转换。

3.1 干扰中断概率约束转换

对于满足独立同分布、有界且随机的信道不确定参数，伯恩斯坦法[15-17]能有效地对中断概率约束条件进行凸近似转换。考虑一般情况，定义向量p={pnk}，其中概率约束可表示为

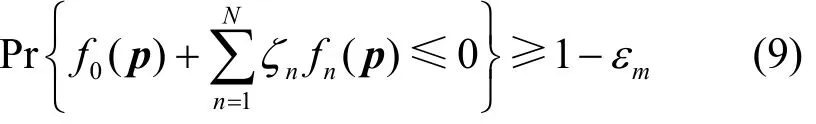
其中，ζn是一个服从边缘分布为ξn的随机变量；fn(p)是p的函数，且在p中是仿射的。对于边缘分布ξn，向量ζ的元素ζ1,…,ζN是彼此独立的，且具有相同的上下界。边缘分布ξn的上下界属于[-1,1]，这意味着ζn在区间[-1,1]上变化。因此，可以给出以下保守替换

其中，ρ为伯恩斯坦辅助变量；Ωn(y)≜maxξnlog (∫exp(xy)dξn(x))，它可以保证式(10)是凸的[18]。当Ωn(y)可以被有效估计时，该近似是有效的。通常，可以为Ωn(y)引入上限

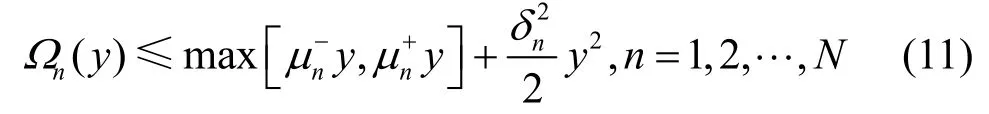
其中，和满足范围，它的值由给定的概率分布簇决定[15]。用这式(11)的上限代替式(10)中的Ωn(·)，并使用算术几何不等式，可得

式(12)可以看作式(9)的保守凸替换。

干扰中断概率中，考虑次用户发射机到主用户接收机链路上的信道不确定性。因此，将看作一个随机变量，假设，其中。引入常数，以保证随机变量上下界属于[ -1,1]。由于，因此，将f0(p)和fn(p)代入式(12)，有

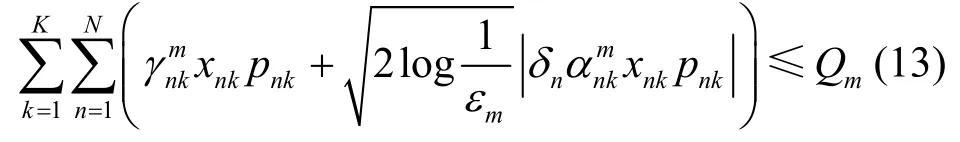
3.2 数据速率中断概率约束转换

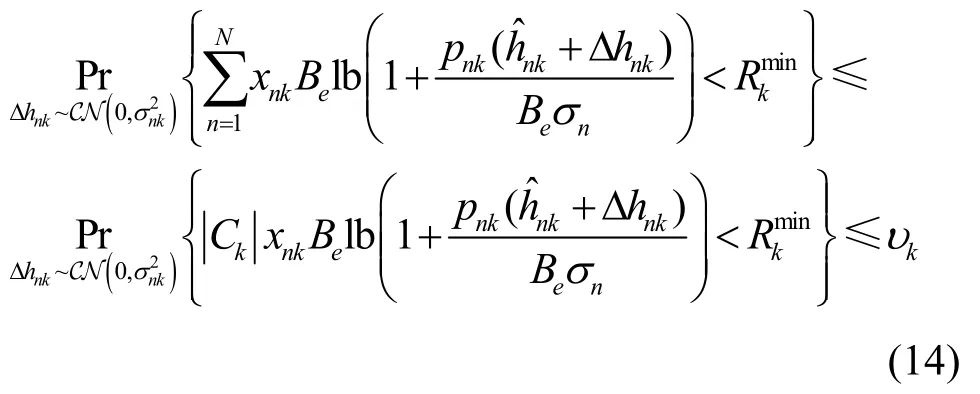
式(14)等价于

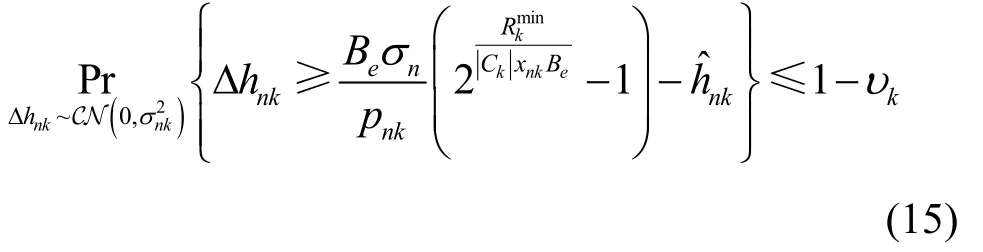
其中，Ck表示分配给第k个次用户的子载波集合，表示分配给第k个次用户的子载波数量。

由于信道误差Δhnk服从以0 为均值、为方差的正态分布，根据Q 函数的性质，可将式(15)转换为

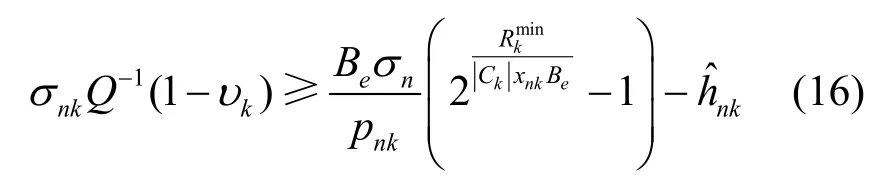
其中，Q-1(·)表示Q 函数的反函数，则有

将式(8)、式(13)和式(17)结合，可以得到中断概率约束经凸转换后的稳健资源分配问题为

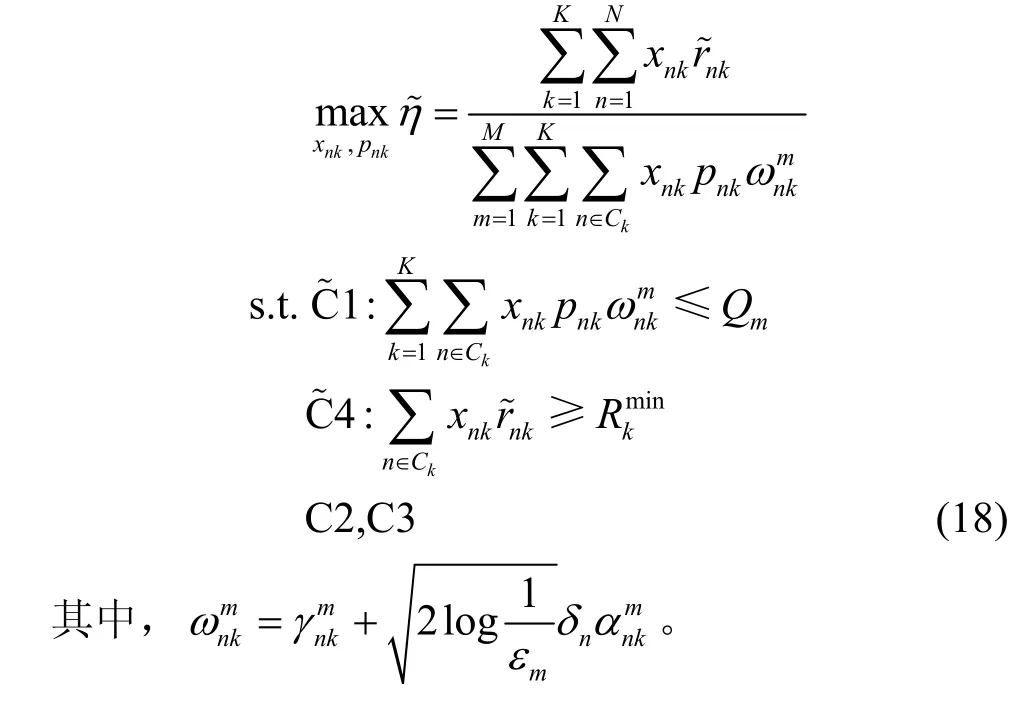
4 稳健资源分配算法

4.1 资源分配算法求解

由于存在二进制整数变量，问题(18)是具有分数目标函数的非凸和混合整数规划问题，该问题难以直接求解。显然，随着用户和子载波数目增加，穷举搜索法会使子载波分配问题计算复杂度很高。为减少整数变量引起的计算复杂性，可以使用变量松弛法[19]来处理该问题。也就是说，可以将整数变量xnk松弛为[0,1] 范围内的连续变量，例如。因此，问题(18)可以转换为

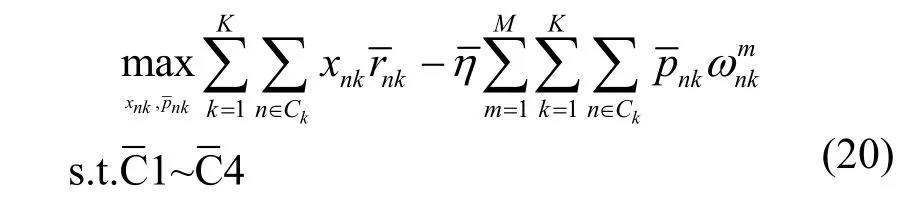
其中，≥0，可以将其视为对主用户的总干扰功率进行加权的定价因子。定义最优值为、和，当且仅当式(21)成立，可得到最大的干扰效率。

因此，首先需要在固定的下获得最优发射功率和子载波分配策略，然后使用最优的功率分配和子载波分配来更新干扰效率，直到获得全局最优解。因此，可以通过使用拉格朗日对偶分解法来解决凸优化问题(20)。定义拉格朗日函数为

其中，λm≥0，φk≥0，ψk≥0和κk≥0是对应约束的拉格朗日乘子。拉格朗日函数可以整理为

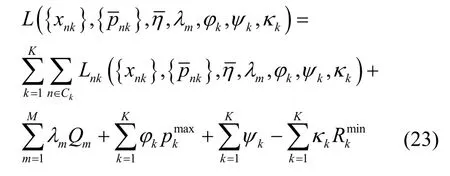
其中，有

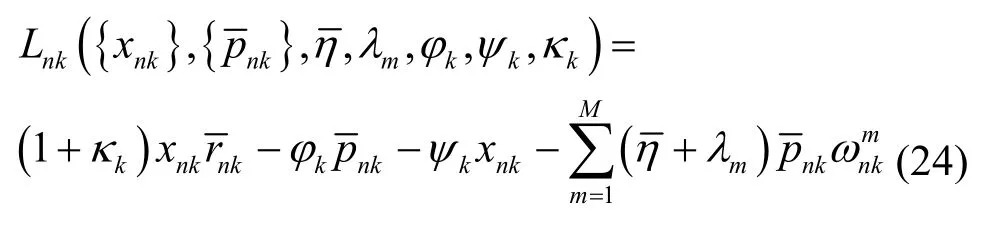
问题(20)的对偶问题为

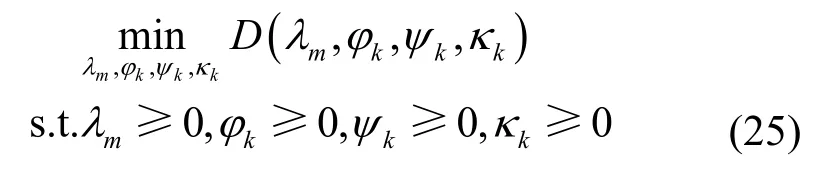
其中，有

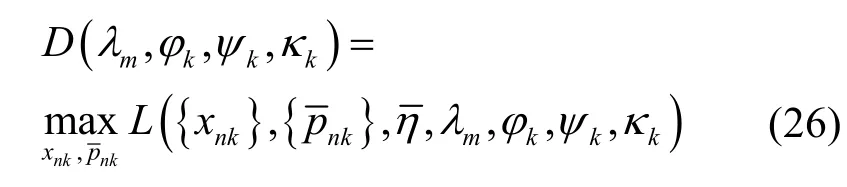
根据式(23)，拉格朗日对偶函数可以被分解为K×N个子问题，这可以被认为是每个子载波n上的每个用户k的优化问题。根据库恩塔克（KKT,Karush-Kuhn-Tucker）条件，最优发射功率为

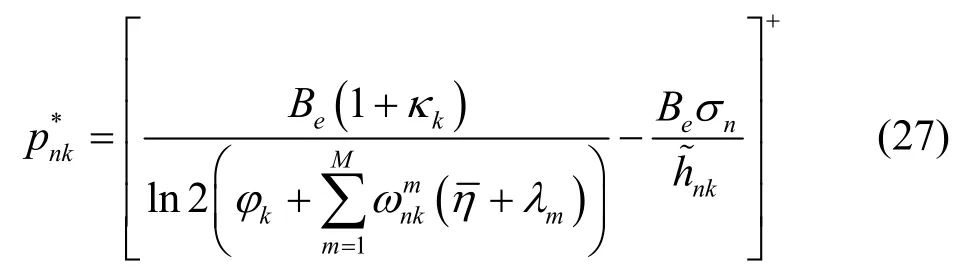
其中，[x]+=max(0,x)。

为了获得子载波分配因子xnk，对拉格朗日函数求偏导数，有

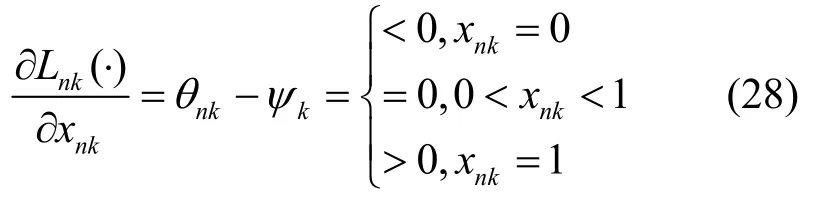
其中，有

第n个子载波总是分配给θnk最大的第k个次用户，也就有

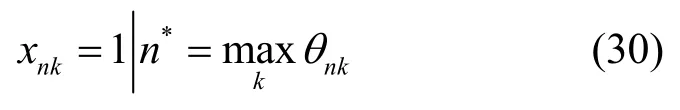
使用次梯度法，拉格朗日乘子可进行如下更新

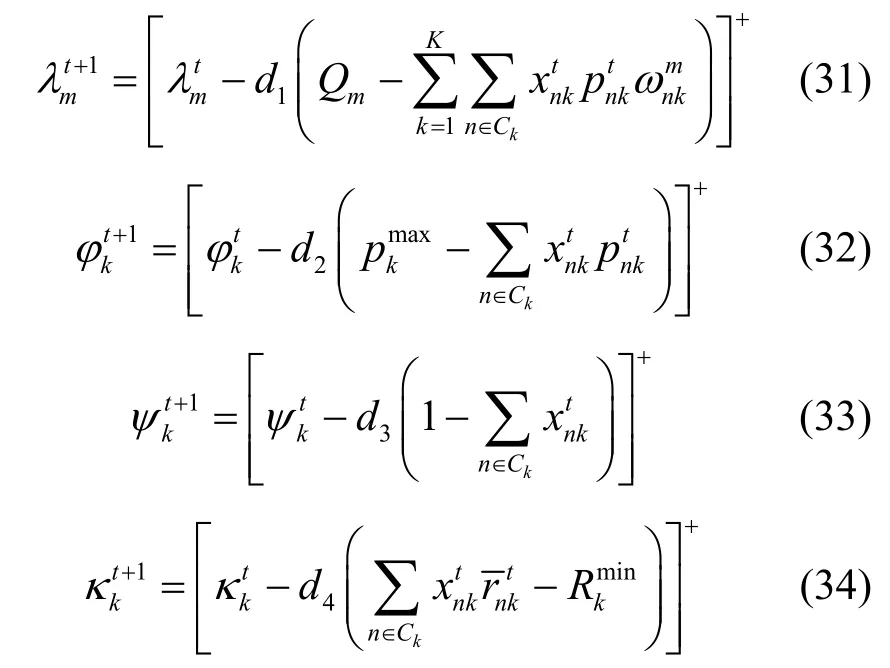
其中，t是迭代次数，d1、d2、d3和d4是步长。

4.2 计算复杂度和稳健性分析

计算复杂度分析。假设外层干扰效率和内层拉格朗日法的最大迭代次数分别为L和T，根据式(29)和式(30)，对每个子载波进行最优分配需要O(NK)次运算；根据式(31)～式(34)，更新拉格朗日乘子λm和其他乘子分别需要 O(M)和 O(K)次运算。因此，拉格朗日乘子的更新的计算复杂度为O(MK)。因为内层迭代次数T是O(MNK2T)的多项式函数，所以算法的总计算复杂度为O(LMNK2T)。通过选择合适的步长，对偶算法可以很快收敛[21]。基于迭代的稳健资源分配算法的具体步骤如算法1 所示。

算法1基于迭代的稳健资源分配算法

山林散养珍珠草鸡产业养殖集中化水平正在由低向高发展，“协会+农户”型组织形式已形成，“工作队+村干部+农户”分红模式初显成效，“农家乐+休闲茶园+协会”、“农家乐+休闲茶园+农户”销售模式不断创新完善。

3)初始化拉格朗日乘子及对应步长，定义内层最大迭代次数T，初始化内层迭代次数t=0 ；

4)while 所有拉格朗日乘子收敛精度都大于ϖ和t≤T，do

5)form=1:1:M

6)fork=1:1:K

7)forn=1:1:N

8) 根据式(27)计算最优发射功率pnk；

10)根据式(31)～式(34)更新拉格朗日乘子λm,φk,ψk和κk；

11)end for

12)end for

13)end for

14)更新t=t+1；

15)en d while

16)更新l=l+1 和；

17)end while

稳健性分析。为了反映信道不确定性对系统性能的影响，本文分析了稳健方案和非稳健方案目标函数的性能差距。根据文献[22]中的灵敏度分析，当参数不确定性非常小时，可以假设非稳健情况下的最优值和稳健情况相等。因此，根据式(23)和式(24)，容易得到总干扰功率的性能差距为

如果估计误差很小时，根据泰勒级数展开法，有

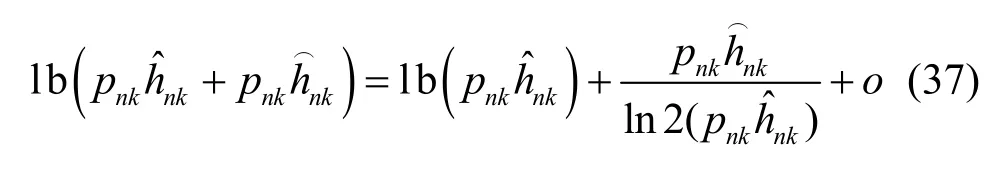
其中，o代表高阶无穷小量。将式(37)代入式(36)中，有

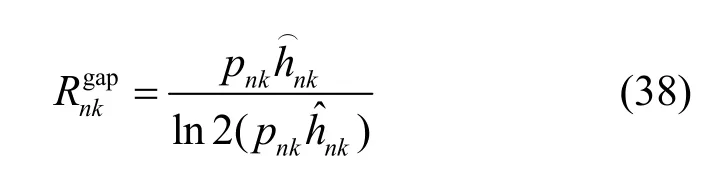
定义系统总干扰效率的性能差距为Lgap=Lrobust-Lnon-robust，并设置初始干扰效率η=0,根据式(23)和式(24)，稳健方案和非稳健方案的性能差距为

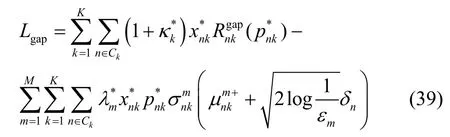
5 仿真结果与分析

本节针对多用户认知网络对所提出的算法进行仿真分析。假设网络中存在3 个次用户，2 个主用户。系统子载波个数N=16，系统总带宽Be=1MHz[7]，每个子载波上的背景噪声功率σn=1×10-8W。次用户对主用户干扰功率阈值Qm=1×10-3W[8]。传输信道增益和干扰信道增益在区间(0,1]内随机取值[23]。伯恩斯坦近似法中，取

图1 给出了算法的收敛性能情况，次用户的最大发射功率阈值max0.010kp=W，次用户的最小数据速率门限。从图1 可以看出，算法在经过大约15 次迭代之后就收敛，具有较好的收敛性。在收敛之后能够满足次用户最大发射功率约束和次用户最小速率约束门限，这说明本文算法可以很好地保障次用户的通信质量。

图1 算法收敛性能

图2 给出了不同传输增益信道估计误差σnk和次用户中断概率门限kυ下，干扰效率和次用户最小数据速率之间的关系。从图2 可以看出，在各种情况中，随着次用户最小数据速率门限的增大，干扰效率逐渐降低。这是因为为了满足最小数据速率门限要求，次用户需要提升发射功率，这会导致次用户会对主用户产生更大的干扰，引起干扰效率的降低。另一方面，传输增益信道估计误差σnk越大，干扰效率越低。这是因为随着信道估计误差增大，次用户需要提升发射功率以克服信道不确定性，导致干扰效率降低。干扰效率随着次用户中断概率门限υk的升高而增加，这是由于次用户的中断概率门限越大，也就越不容易发生中断，允许次用户以较低的发射功率进行传输。

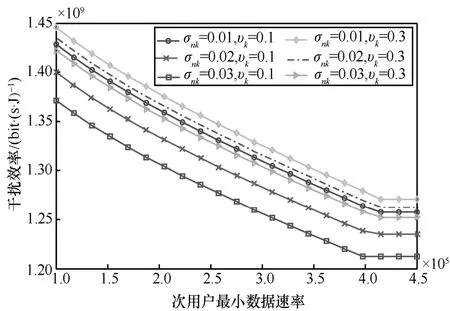
图2 不同传输增益条件下，干扰效率与次用户最小数据速率的关系

图3 给出了不同干扰增益信道估计误差和主用户中断概率门限下，干扰效率和次用户最小数据速率之间的关系。从图3 可以看出，所有情况下随着次用户最小数据速率的增大，干扰效率都是先下降再趋于稳定值。这是由于受到主用户干扰功率阈值的约束，发射功率不能一直增加，因此最终都会趋于稳定。而随着干扰增益信道估计误差越大，干扰效率越快趋于稳定。这是因为更大的信道不确定性会更大程度地限制次用户的发射功率，因此发射功率的可行域更小。此外，主用户中断概率门限越大，干扰效率越慢趋于稳定。这是由于较大的主用户中断概率门限会扩大发射功率的可行域。

图4 给出了不同次用户的最大发射功率阈值下，干扰效率随传输增益信道估计误差和次用户中断概率门限的关系。从图4 可以看出，次用户的最大发射功率阈值增大，干扰效率随之降低。干扰效率随着传输增益信道估计误差的增加而降低，随着次用户中断概率门限的提升而升高。

图3 不同干扰增益条件下，干扰效率与次用户最小数据速率的关系

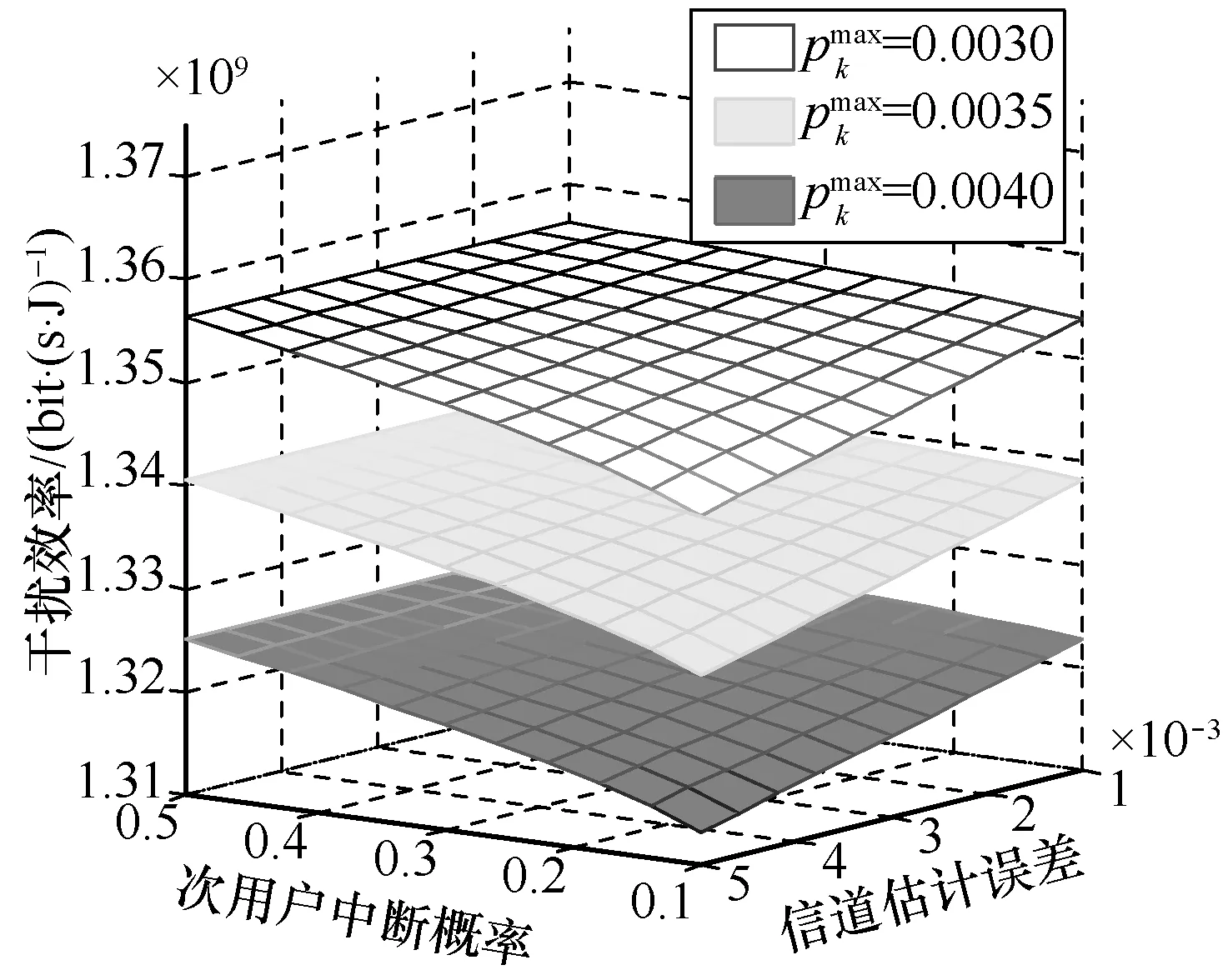
图4 干扰效率与信道估计误差及次用户中断概率的关系

根据现阶段认知OFDMA 网络资源分配问题的研究情况，为进一步验证算法的性能，将本文算法与现有能效最大化算法[24]和速率最大化算法[25]进行性能对比。为体现稳健设计对算法性能的影响，同时定义本文最优算法为

图5 给出了不同算法下，干扰效率与次用户最小数据速率关系。从图5 可以看出，本文最优算法具有最高的干扰效率，本文稳健算法的干扰效率略低于最优算法，能效最大算法也具有可观的性能，而速率最大算法的干扰效率性能最差。这是因为本文算法以次用户网络总干扰效率作为优化目标，在系统参数相同的条件下，算法设计的结果会使本文算法的干扰效率与对比算法相比更高。

图6 给出了不同算法下，能量效率与次用户最小数据速率关系。从图6 可以看出，能效最大算法具有最好的能效性能，本文最优算法和稳健算法也具有较好的能效性能，而基于速率最大化的算法能效性能最差。

图5 不同算法下，干扰效率与次用户最小数据速率的关系

图6 不同算法下，能量效率与次用户最小数据速率的关系

图7 给出了不同算法下，主用户实际中断概率与信道估计误差上界的关系。由图7 可知，主用户实际中断概率随着信道估计误差上界的增大而升高。这是因为信道估计误差上界越大，意味着对主用户干扰链路的实际信道不确定性更大，这会增加主用户的实际中断概率。另一方面，当信道估计误差上界较大时，在其他3 种考虑完美信道状态信息的算法下，中断概率都超过了主用户的中断概率门限值。只有本文稳健算法的中断概率很好地控制在中断概率门限以下，这说明本文稳健算法具有良好的稳健性。相比于另外2 种考虑完美信道状态信息的对比算法，由于本文最优算法也以干扰效率作为优化目标，可以减少次用户对主用户的干扰，因此主用户中断概率低于2 种对比算法。

6 结束语

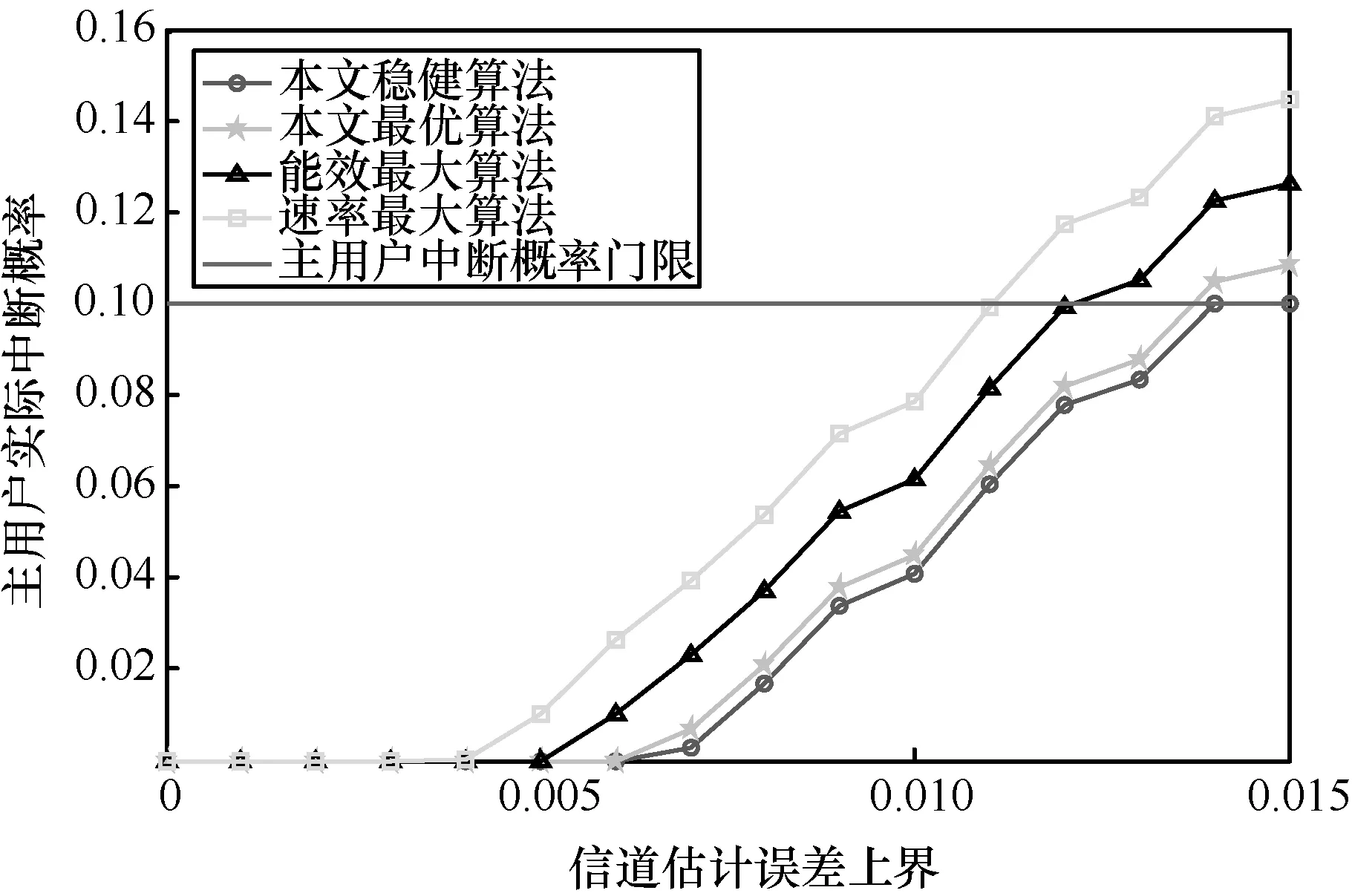
图7 不同算法下，主用户实际中断概率与信道估计误差上界的关系

本文针对基于干扰效率最大的认知OFDMA 网络稳健功率与子载波分配优化问题进行研究。考虑用户QoS 约束、发射功率约束和子载波分配约束，建立基于中断概率的干扰效率最大稳健资源分配模型。利用伯恩斯坦近似和Q 函数性质，将原问题中基于中断概率的约束转换成了凸约束。接着利用Dinkelbach 法，将原基于中断概率的非凸问题转换成等价凸优化问题，利用拉格朗日对偶函数法求得解析解，并对算法进行了计算复杂度和稳健性分析。仿真结果表明，本文算法具有很好的干扰效率和稳健性。