基于改进余弦相似度的协同过滤推荐算法

李一野，邓浩江

(1.中国科学院声学研究所国家网络新媒体工程技术研究中心，北京 100190； 2.中国科学院大学，北京 100049)

1 概 述

随着互联网的发展，电子商务、社交媒体网站等信息平台上都出现了信息过载的问题，推荐系统在各种平台上被广泛使用，有效地缓解了信息过载的现象。在推荐系统中所使用到的推荐算法，主要分为基于内容(content-based)的推荐算法[1]、协同过滤(collaborative filtering)算法[2]以及混合推荐算法[3]。其中，基于内容的推荐算法是根据用户的历史评分行为数据做推荐[4]，在数据稀疏的情况下，算法需要根据少量的用户历史评分行为做推荐，但用户行为数据的稀疏性使算法难以学习到用户潜在的偏好，从而不能够完整地获取用户的偏好，使得推荐的结果偏差过大。协同过滤推荐算法包含基于近邻(nearest-neighbor)[5]的协同过滤推荐算法[6]、基于模型(model-based)的协同过滤推荐算法[7]。

基于近邻的协同过滤推荐算法利用评分的相关性作为依据，若2个用户对同一个物品评分，则将它们视作近邻用户，并推荐被该近邻用户所评价过的物品。这使得基于近邻的协同过滤推荐算法在稀疏的数据中往往存在问题[8]，其中数据的稀疏性，一方面体现在用户评价过的物品数量大多数是有限的，只占物品数量中的较小部分；另一方面体现在，只有少量的物品被大多数用户评价过[9]。这就会造成正样本(positive sample)的数量很少，而负样本(negative sample)则占了大多数的情况，对推荐系统造成不好的影响。

而基于模型的协同过滤推荐算法，是通过对已有的数据进行学习，继而得到用户和物品的潜在特征，然后通过潜在特征构建模型，利用模型来进行推荐。在对潜在特征的学习过程中，由于训练过程中所采用的训练样本会对算法的结果产生影响，可能会造成过拟合。为了避免出现过拟合的现象，算法在训练过程中同时采用正样本和负样本进行训练。这就会导致一种情况的出现：每个用户都具有较多的未知样本和负样本，当2个基于正样本原本不相似不互为近邻的用户[10]，在采用负样本训练时有一定的概率出现因为负样本产生了相似度的情况。在数据稀疏的情况下，大多数用户的负样本相互之间都有交集。这种情况下所产生的近邻会导致在多次迭代后学习到的用户的潜在特征越来越相似，从而导致难以区分出与用户喜好真正相似的用户。

在数据稀疏的情况下，基于模型的协同过滤推荐算法存在分类准确性低的问题[11]，为了解决这一问题，本文提出一种基于改进余弦相似度[12]的协同过滤推荐算法，将数据经嵌入层(embedding layer)转换为特征矩阵[13]，对其计算后得到改进余弦相似度矩阵，将其和单位矩阵之间的均方误差作为损失函数。这种方法可以有效地增加正样本在训练过程中的影响，减小负样本在训练过程中的影响，提高数据稀疏情况下分类的准确性。

2 相关工作

基于模型的协同过滤推荐算法，主要是通过机器学习方法或概率统计模型来建立模型(例如贝叶斯模型、图模型、潜在语义模型、决策树模型等模型)[14]，然后通过模型预测目标用户的偏好。近年来，因子分解机(Factorization Machine， FM)模型和在其基础上衍生的场感知因子分解机(Field-aware Factorization Machine， FFM)模型在实际场景中得到广泛的应用。FM模型可以在数据稀疏的情况下组合特征。常见的多项式模型如式(1)所示：

(1)

由二次多项式模型可知，组合特征相关参数共有n(n-1)/2个。在数据集较为稀疏的情况下，xi或xj为0的情况非常多，ωij很难经过训练得出。

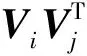
(2)

由ωij构成的矩阵如下：

(3)

对于交叉项利用下式进行化简，然后利用随机梯度下降SGD求解：

(4)

FFM模型在FM模型的基础上进行了优化，引入了类别(field)的概念，假设样本的f个类别共计存在n个特征，则对于FFM模型的二次项而言就有n×f个隐向量。当FMM模型的所有特征都属于一个类别时，FFM可以视作FM模型。FFM模型方程如下：

(5)

FFM的二次参数为n×f×k个，其中，n为特征数量，f为类别数量，k为隐向量维数。与FM模型相比，FFM模型中的特征都有几个不同的隐向量，其在稀疏度较大的输出处理上效果更好。而且FFM模型支持并行化处理，其运行时间较短。但这2种模型在处理高阶特征和低阶特征的交互信息方面存在不足。

目前，深度因子分解机(Deep Factorization Machine， DeepFM)模型在探索数据潜在特征[15]，同时学习高阶特征和低阶特征的交互信息方面有良好的效果。DeepFM模型通过融合因子分解机和深度神经网络，同时学习低阶特征和高阶特征之间的交互信息。DeepFM模型由深度神经网络部分(Deep component)和因子分解机部分(FM component)这2个部分组成。深度神经网络部分负责提取低阶特征，因子分解机负责提取高阶特征。这2个部分共享相同的输入。DeepFM模型最终预测结果时将深度神经网络部分和因子分解机部分这2个部分的预测结果输入激活函数：

(6)

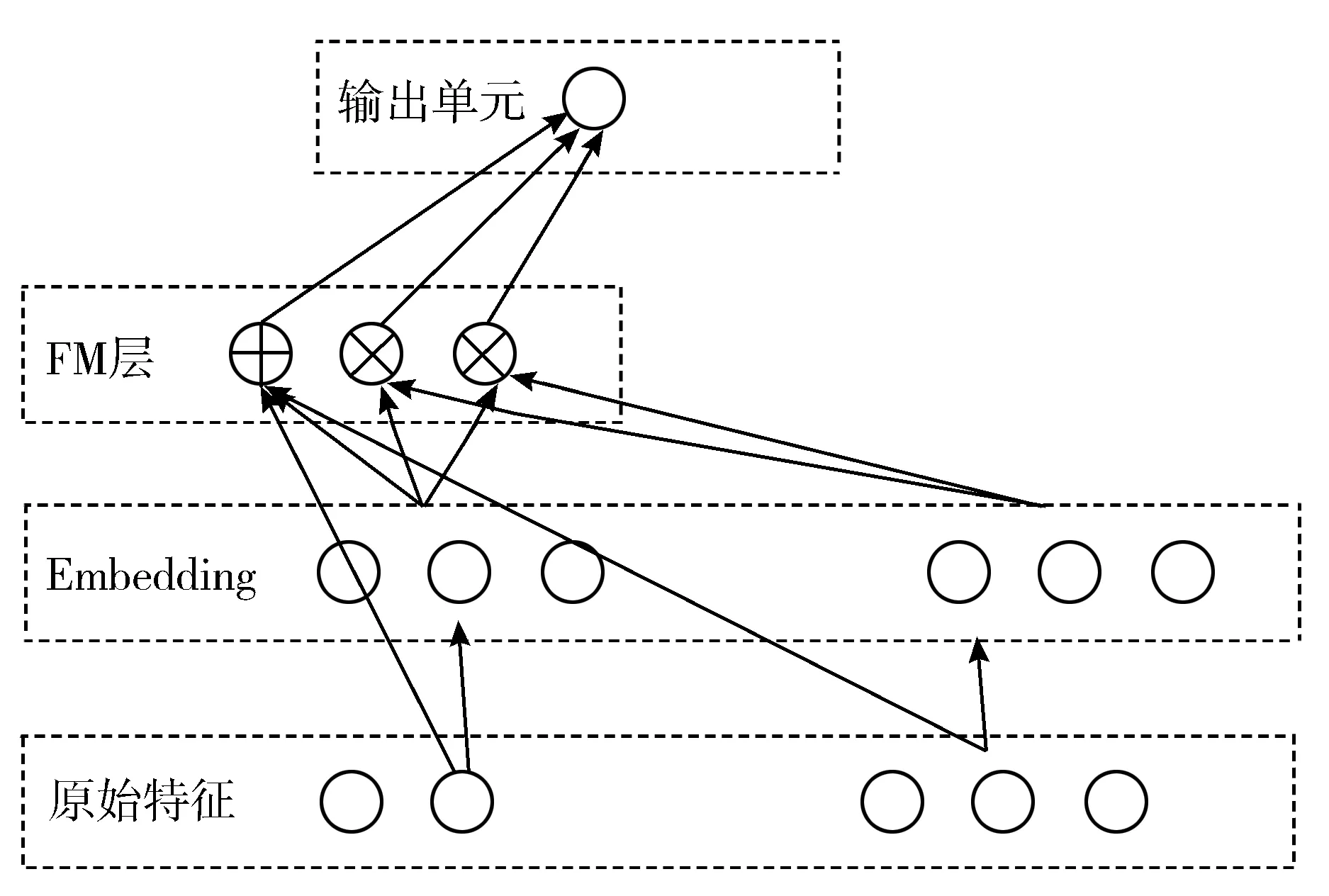
图1 因子分解机部分

图1所示是因子分解机部分的结构。因子分解机部分在学习特征的线性交互的同时也利用隐向量的内积学习二阶交互特征。该部分输出如下：

(7)

深度神经网络部分的结构如图2所示，它是一种前馈神经网络，主要作用是学习高阶特征的交互。首先引入一个嵌入层来将非常稀疏的输入向量压缩为较为稠密的低维向量。在嵌入层，每个特征都会被映射为低维向量，这些向量的长度相等，既可以作为隐向量在因子分解机部分中使用，也可以作为输入在深度神经网络中使用。

图2 深度神经网络部分

嵌入层[16]输出公式如下：

a(0)=[e1,e2,…,em]

(8)

其中，输入特征的个数为m，ei为输出特征中第i个特征的嵌入值，该部分网络前馈的过程可以表示如下：

a(l+1)=σ(W(l)·a(l)+b(l))

(9)

其中，l为神经网络层的深度，σ为激活函数，W(l)、a(l)、b(l)分别为权重、隐层输出和第l层的偏置。深度神经网络随后生成低维度的特征向量输入激活函数，最终的输出如下：

yDNN=σ(W|H|+1·a|H|+b|H|+1)

(10)

其中，|H|为隐藏层的数量。

嵌入层结构如图3所示，嵌入层产生的向量长度相同，从因子分解机得到的隐向量Rik是嵌入层网络的权重。

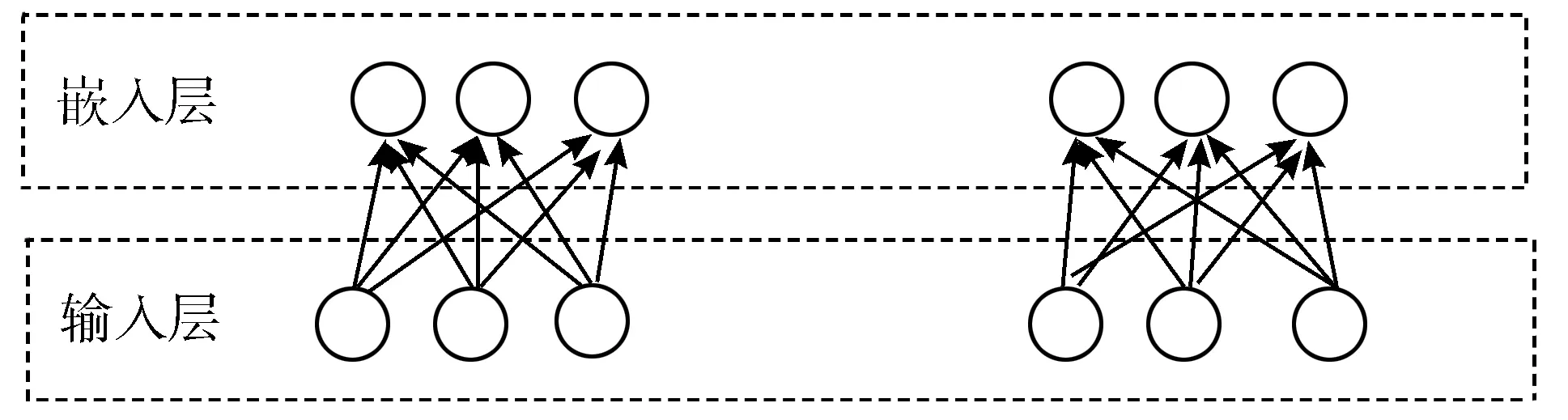
图3 嵌入层结构

3 基于改进余弦相似度的协同过滤推荐算法

基于改进余弦相似度的协同过滤推荐算法，是将数据利用嵌入层进行映射从而转换为特征矩阵，将对其计算后得到的改进余弦相似度矩阵和单位矩阵之间的均方误差作为损失函数，以此来减小负样本在训练过程中对学习潜在特征造成的不利影响，提高数据稀疏情况下分类的准确性。

在实际的应用场景中，数据的稀疏性是指由于数据规模非常大，使得用户对物品的选择之间存在的重叠非常少。大部分评分数据都是未知的，以Movielens-10M数据集为例，评分数据以0.5分为间隔在0.5～5分之间分布。

在实际场景中，不同的用户在评分标准上存在一定程度的不同[17]，有的用户评分标准比较严格，即使对偏好的物品也会给出偏低的评分，而有的用户标准相对较低，对于偏好程度较低的物品给出的评分依然会很高，这种情况会影响到计算相似性。因此要对数据做归一化处理。常用的归一化方法有最小最大归一化(Min-Max Normalization)[18]和1标准差归一化(z-score Normalization)[19]。

最小最大归一化是将数值线性变换到[0,1]之中。变换公式如下：

(11)

其中，max和min分别为数据样本的最大值和最小值，在数据集引入新的数据时，会引起最大值和最小值产生变化，从而需要重新定义。

而1标准差归一化是使数据变为0均值、1标准差，其公式如下：

(12)

其中，x是原始数据，z为归一化后的数据，对于M×N的矩阵，M为样本数，N为特征的个数，需要变换的均值和方差是矩阵的均值和方差。

在数据的处理过程中，对数据采用1标准差归一化处理。

余弦相似度[18]的计算公式如下：

(13)

其中，x1k、x2k分别是2个向量在第k个维度上的值。当2个向量越相似时，两者之间的夹角越小，其相似度越大。当相似度为负数时2个向量为负相关。

余弦相似度存在的问题是对数值不够敏感，因其主要是区分向量间的方向差异，难以衡量向量不同维度在数值上的差异，这使得评价用户相似度时出现偏差。以MovieLens数据集中用户对电影的评分为例[20]，A和B这2个用户对X和Y这2部电影的评分分别为(2，1)和(5，4)，二者的余弦相似度为0.98，从结果上看用户A和B的偏好非常相似，但是从评分上看用户A对X和Y这2部电影评价并不算高，而用户B则十分偏好这2部电影，由于余弦相似度对数值不够敏感，因此使用其作为计算用户偏好相似度的依据时会出现一定的偏差。

为了修正这种偏差，本文采用改进余弦相似度来衡量[21]，即在向量的每个维度上都减去用户对电影的评分均值，例如用户A和用户B对电影的评分均值为3，修正后为(-1，-2)和(2，1)，二者的改进余弦相似度为-0.8，这反映用户A和用户B的偏好存在差异，这个结果更符合实际情况。在实验中对数据都是作归一化处理。

(14)

将数据经嵌入层转换为特征矩阵，对其计算后得到改进余弦相似度矩阵，位于矩阵第i行j列的元素，代表的是第i个用户与第j个用户之间的改进余弦相似度。

在数据稀疏的场景下，推荐系统面临的是复杂的非线性映射问题，所以本文使用的损失函数主要用于解决非线性问题。

使用均方误差(Mean Square Error)作为损失函数，其公式如下：

(15)

在得到改进余弦相似度矩阵之后，进而计算它和单位矩阵之间的均方误差，将其作为损失函数，并用该部分的损失函数结合基线模型的损失函数，而该部分的损失函数，在两者中所占的权重较小。

这种基于改进余弦相似度的协同过滤推荐算法，通过加入改进余弦相似度进行约束的优化问题的构造，能够令与目标用户偏好真正相似的用户在对样本进行训练的过程中，利用正样本产生更大的相似度，使其从学习到的相似潜在特征中区分出来，提高数据稀疏情况下分类的准确性。

4 实验结果分析

4.1 数据集

本文的实验数据采用MovieLens-10M数据集，在实验中，该数据集被用于评价基于模型的协同过滤算法推荐效果，数据集中包含了10681部电影的信息、71567个用户的信息和10×106条评分数据。每条评分记录有用户ID、电影ID、评分、时间戳4个属性。电影评分为0.5～5，以0.5为间隔，评分越低时，用户对该电影的偏好度越低[22]。

在选取实验数据时，选择每个用户的70%评分信息作为训练数据，选择其余的30%作为测试数据。数据集评分密度为1.3%，评分密度是指平均每个用户评价多少个项目，可见Movielens-10M数据集具有显著的稀疏性。在实验中对MovieLens-10M数据集采用五折交叉验证(5-Fold Cross Validation)，共进行5次划分，在每一折实验中，基于训练集数据预测测试集数据，并通过比较预测评分与真实评分得出每一折的MSE值，最后取结果的平均值。

4.2 实验环境和评价指标

本文实验所采用的环境为Linux版本Ubuntu 16.04，采用GPU进行训练，显卡为Tesla K40。参数设置上DeepFM模型和在DeepFM模型基础上改进的基于改进余弦相似度的协同过滤推荐算法均使用TensorFlow实现。对于基线算法和本文提出的优化方法，FM隐向量的维数均为8，在深度神经网络部分的网络层数分别为10和5，学习速率设置为0.01，批处理大小为100，基于改进余弦相似度的协同过滤推荐算法的损失函数与DeepFM模型的损失函数相比所占权重较小，实验中设为0.0001。

本文采用AUC(Area Under the ROC Curve， ROC曲线下面积)和对数损失函数(Logloss)作为评价指标来描述推荐效果。

受试者工作特性曲线 (Receiver Operator Characteristic Curve， ROC曲线)是反映二分类器的分类性能的指标[23]。在常见的二分类预测问题中，当分类预测的结果和实际结果同时为正类时，被称作真阳性；当分类预测的结果和实际结果同时为负类时，则称作真阴性。在预测结果为负类，实际结果为正类时称为假阴性。当预测结果为正类，而实际结果则为负类时，称为假阳性，这种情况下的样例，其在实际结果为负类的全部样例中的比率被称作假阳率，而正确预测为正类的实例在所有实际结果为正例的实例中的比例被称作真阳率。

假阳率和真阳率分别对应着在ROC空间中的横轴坐标和纵轴坐标。同样一个二分类器，随着阈值t的不断改变，其对应的坐标点的连线即为该分类器的ROC曲线。在ROC空间中，曲线在左上方，其分类器性能较好，曲线在右下方，其分类器性能较差[24]，点(0，1)代表的分类器，是最完美的，点(1，0)代表的分类器是一个最糟糕的分类器。

ROC曲线下面积AUC是衡量分类器分类精度的重要评价指标[25]，ROC曲线下的区域面积，被定义为AUC，其越大代表分类器分类能力越强。分类器在AUC=1时最完美，在AUC=0.5时，分类器没有价值，因为其结果是随机的。

当分类器的输出结果为样本属于正类的置信度时，AUC为随机抽取一对样本其中正样本的置信度大于负样本置信度的概率。AUC可以通过直接计算ROC曲线下的面积得到，也可以通过计算正样本置信度大于负样本置信度的概率得到，按照置信度从大到小排序，正样本的置信度大于负样本置信度的概率根据式(16)计算：

(16)

其中，M为正样本数，N为负样本数，置信度最大的样本rank为n，次大的样本rank为n-1，按照这个规律类推。实验中，将正样本定义为评分大于2.5的样本，其他的样本定义为负样本。

AUC在评价分类器精度时被普遍地使用，AUC在类不平衡的情况下十分稳定，能够比较准确地体现特征对于实例分布的区分程度。

对数损失函数Logloss，也被称为交叉熵损失函数或者逻辑回归损失函数，主要被当作是评价二分类问题模型的准确度的评价指标，其定义如式(17)所示：

(17)

其中，N为样本总数，yi为第i个样本的标签，hi为模型预测点击的概率。

AUC和对数损失函数Logloss是在评价基于模型的协同过滤推荐算法中常被用到的评价指标。

4.3 实验结果及分析

本文对实验结果从有效性和性能这2个方面对模型进行分析和对照。

为了容易在图形上进行直观展示，对于在FM模型、FFM模型和DeepFM模型方案上分别实现的基于改进余弦相似度的协同过滤推荐算法，记为“FM+”、“FFM+”和“DeepFM+”。模型的有效性对比如图4～图6所示。

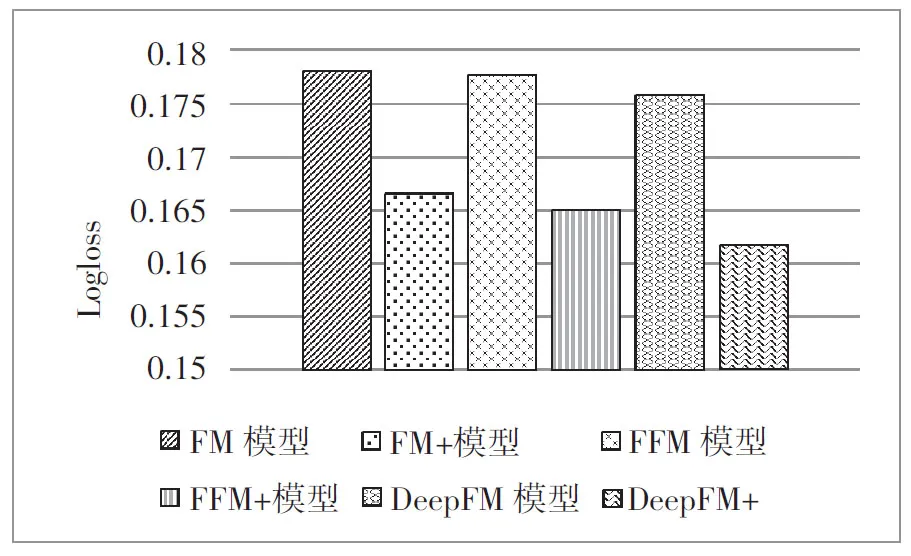
图4 各模型Logloss结果对比

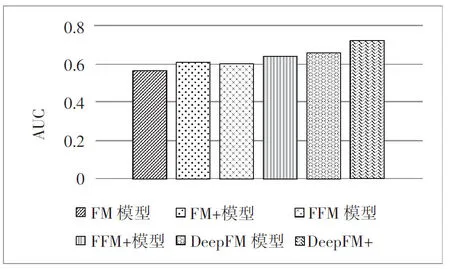
图5 各模型AUC结果对比

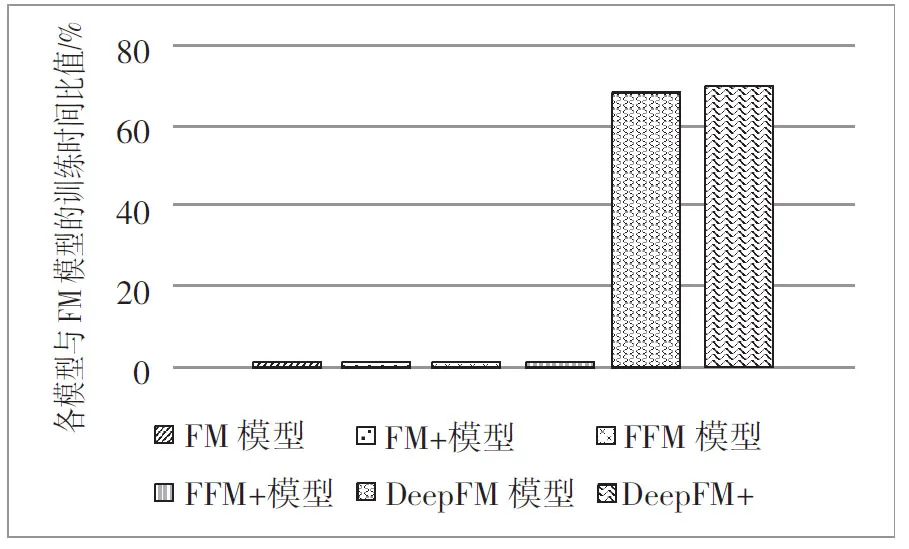
图6 各模型与FM模型的训练时间比值

根据实验结果，在Logloss和AUC指标的表现上基于改进余弦相似度的协同过滤推荐算法均要好于基线算法，其中“FM+”模型比FM模型在AUC上提升8.32%，在Logloss上降低6.56%。“FFM+”模型比FFM模型在AUC上提升5.68%，在Logloss上降低7.2%。“DeepFM+”模型比DeepFM模型在AUC上提升10.04%，在Logloss上降低8.1%。表明本文提出的算法有效地提高了分类的准确性。

算法的运行效率在实际场景中也十分重要。本文以FM模型为基准来衡量每个模型的训练时间。训练时间评价指标如公式(18)所示：

(18)

在训练时间上，“FM+”模型比FM模型多5.2%，“FFM+”模型比FFM模型多6%，“DeepFM+”模型较DeepFM模型多3%。这组对照实验表明，在可以明显提高推荐效果的情况下，本文提出的基于改进余弦相似度的协同过滤推荐算法所增加的训练时间并不多。

5 结束语

在数据稀疏的情况下，2个基于正样本原本不相似的用户在传统的协同过滤推荐算法中采用负样本训练时，会有一定概率出现因为负样本产生了相似度的情况，从而使算法在多次迭代后学习到的用户的潜在特征越来越相似，导致难以区分出与用户喜好真正相似的用户、分类准确性低的问题。

为了解决在数据稀疏的条件下，基于模型的协同过滤推荐算法存在的分类准确性低的问题，本文提出了一种基于改进余弦相似度的协同过滤推荐算法，将数据经嵌入层转换为特征矩阵，将对其计算后得到的改进余弦相似度矩阵和单位矩阵之间的均方误差作为损失函数。

实验结果表明，在AUC和Logloss指标的表现上，本文提出的基于改进余弦相似度的协同过滤推荐算法均优于基线算法。而与此同时，基于改进余弦相似度的协同过滤推荐算法所产生的训练时间开销也都是可以接受的。通过这种方法，可以有效地提高正样本在训练过程中的影响，减小负样本在训练过程中的影响，提高数据稀疏情况下分类的准确性。在未来的工作中，将研究如何将更多的样本信息也融入改进算法之中，以此来进一步地提高算法的推荐性能。