物体自由入水的多参数影响分析

2020-02-08刘双武雨嫣何广华谢滨阳

哈尔滨工程大学学报 2020年1期

刘双，武雨嫣，何广华，谢滨阳

(1.哈尔滨工业大学机电工程学院，黑龙江哈尔滨 150001; 2.哈尔滨工业大学(威海) 船舶与海洋工程学院，山东威海 264209)

入水砰击问题广泛存在[1],砰击时间历程短、压力峰值大，易引起结构失效或破坏，对结构物局部或整体的强度均会产生较大危害，因此对结构物入水砰击问题进行研究具有十分重要的意义。关于结构物入水问题的研究最早始于19世纪末。Worthington等[2]对不同表面粗糙度球体的入水过程以及入水喷溅、入水空泡闭合等现象进行了系统的研究。Von Karman[3]对水上飞机浮箱降落过程中撞击水面所受的砰击力进行了理论研究。Wagner[4]在Von Karman砰击理论基础之上，提出了经典的Wagner势流砰击理论。其余还有Dobrovol skaya[5]、Bihnam等[6]、Zhao等[7]、Hu等[8]。陈翔等[9]采用MPS求解器研究了二维楔形体在不同粒子布置方式下的入水问题。张岳青等[10]采用LS-DYNA软件对楔形体及弧形体入水问题进行了模拟。其他有张军等[11]、孙辉等[12]。王永虎等[13]、李云波等[14]采用势流方法研究入水问题，张于维等[15]、王易君等[16]使用Fluent软件研究了结构物入水过程。众多研究为了问题的简化，以研究恒速入水现象居多。本研究基于可自动生成网格的STAR-CCM+和常用软件Fluent对自由入水砰击问题展开了研究。首先建立了2套数值模型以实现自相互验证，通过网格收敛性及速度-压力耦合算法适用性的研究并结合试验值进行比对进一步验证了数值方法的准确性。接着采用2种模型同时模拟了不同入水速度和底升角等参数对楔形体自由入水过程的影响。

1 理论与数值模型

1.1 二维楔形体砰击理论

图1为楔形体入水砰击模型。楔形体的底升角为β，单位长度楔形体的质量为M，入水时刻速度为V0，入水深度为z时，对应的下落速度为V，静水面处半宽为c0，楔形体被液体浸湿部分半宽为c。忽略楔形体重力及浮力的作用，根据动量定理可以得到：

MV0=(M+m)V

(1)

式中m为楔形体单位长度的附加质量。

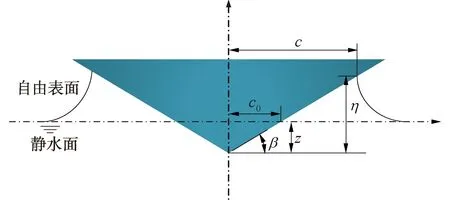
图1 楔形体入水砰击模型Fig.1 Water slamming model of wedge body

将式(1)进行微分可得某一瞬间作用在楔形体的冲击力：

(2)

可见，砰击载荷与入水速度等因素密切相关。

1.2 基本控制方程

控制方程为：

(3)

式中：ρ代表流体密度；t为时间，u、v、w分别表示速度沿x、y、z3个方向上的分量：

(4)

式中：Fbx、Fby、Fbz分别是质量力在3个方向上的分量；pyx为流体内应力张量的分量。式(3)、(4)分别为连续性方程和N-S方程的三维形式，本文的入水问题研究主要关注x-z平面。

2 数值模拟与结果分析

2.1 计算模型的建立

为检验本数值模型的准确性，选用Zhao等[7]模型试验作为参考，图2是试验中的楔形体模型。在楔形体右侧分布有P1、P2、P3、P4、P55个传感器，用来测定测量点的砰击压力随时间变化情况，同时通过测定模型下落时的加速度，计算出模型整体的砰击压力值。表1给出了试验模型的具体参数。图3是2种CFD计算模型所采用的网格。

图2 Zhao等[7]的楔形体试验模型Fig.2 Wedge test model of Zhao et al[7]

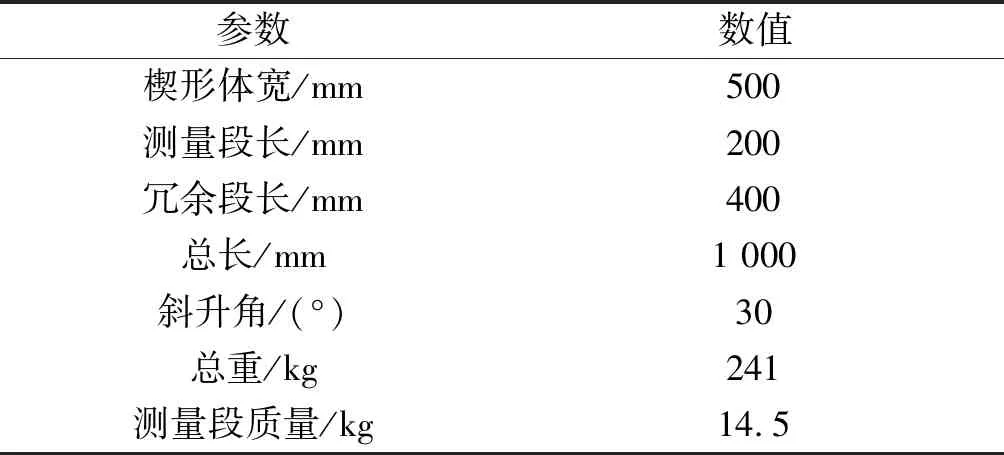
表1 楔形体的主要参数Table 1 Principle parameters of wedge

为减小边界对计算结果的影响，本文计算域宽度取楔形体宽度的10倍，为5 000 mm；高度为5 200 mm；其中空气域高度2 500 mm；液体高度2 700 mm；楔形体的底升角为30°；宽度500 mm；顶端在自由液面上方100 mm处。计算域上方边界为压力出口，其余边界为标准壁面，楔形体在重力加速作用下以一定初速度由空气落入水中。在STAR-CCM+中没有模拟纯二维情况，楔形体取单位厚度。为与试验保持一致，楔形体尖端触水速度均为6.15 m/s。

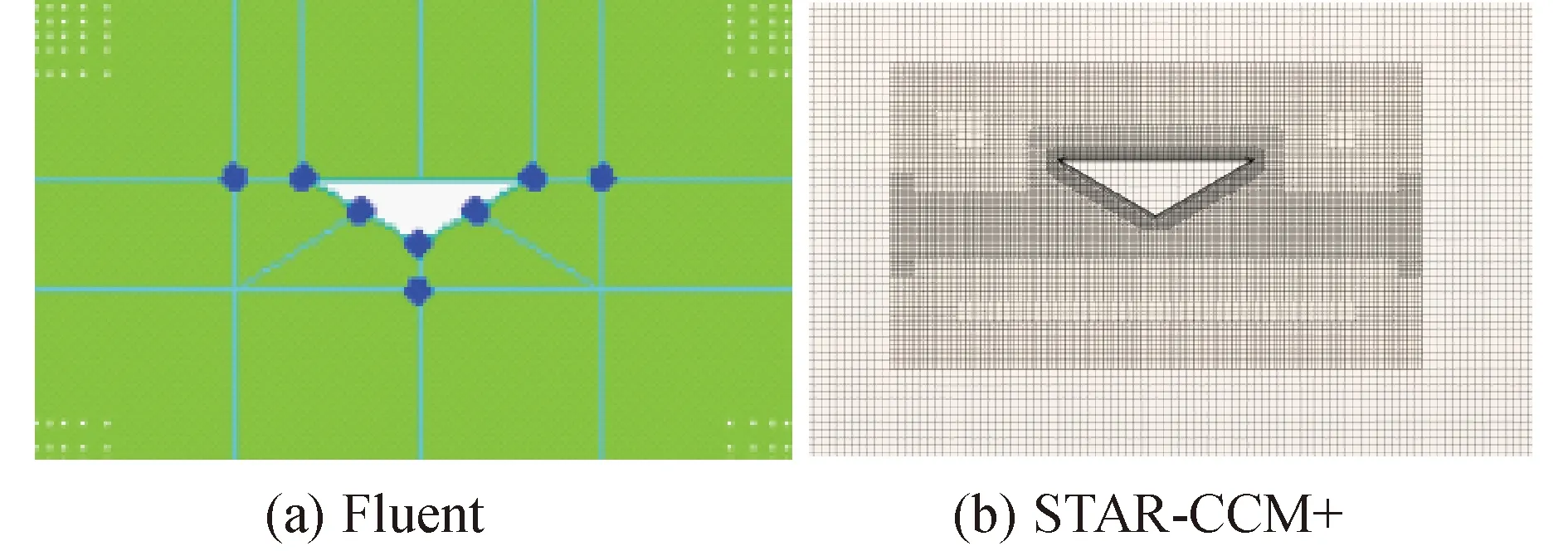
图3 楔形体流场网格划分Fig.3 Computational mesh for water entry of wedge

本Fluent模型基于网格重构技术，采用VOF及6-DOF方式追踪自由液面及楔形体运动，湍流模型采用Realizablek-ω模型；而在STAR-CCM+里，基于重叠网格技术和DFBI方法模拟大尺度运动问题；通过壁面函数法对近壁区Realizablek-ε模型进行处理；采用欧拉多相流模型对空气和水进行建模；采用VOF法捕捉自由液面。

2.1.1 收敛性验证

首先，对2种CFD计算模型的网格收敛性展开了验证。表2、3分别给出了2种计算模型中采用的3种网格。Fluent是通过改变最小网格尺寸来控制网格数量；STAR-CCM+中是通过改变网格基础尺寸来控制网格数量。

表2 Fluent中采用的网格Table 2 Number of grid used in Fluent

表3 STAR-CCM+中采用的网格Table 3 Number of grid used in STAR-CCM+

图4分别给出了Fluent及STAR-CCM+中网格密度对楔形体入水过程速度衰减的影响，同时与试验结果进行比对。

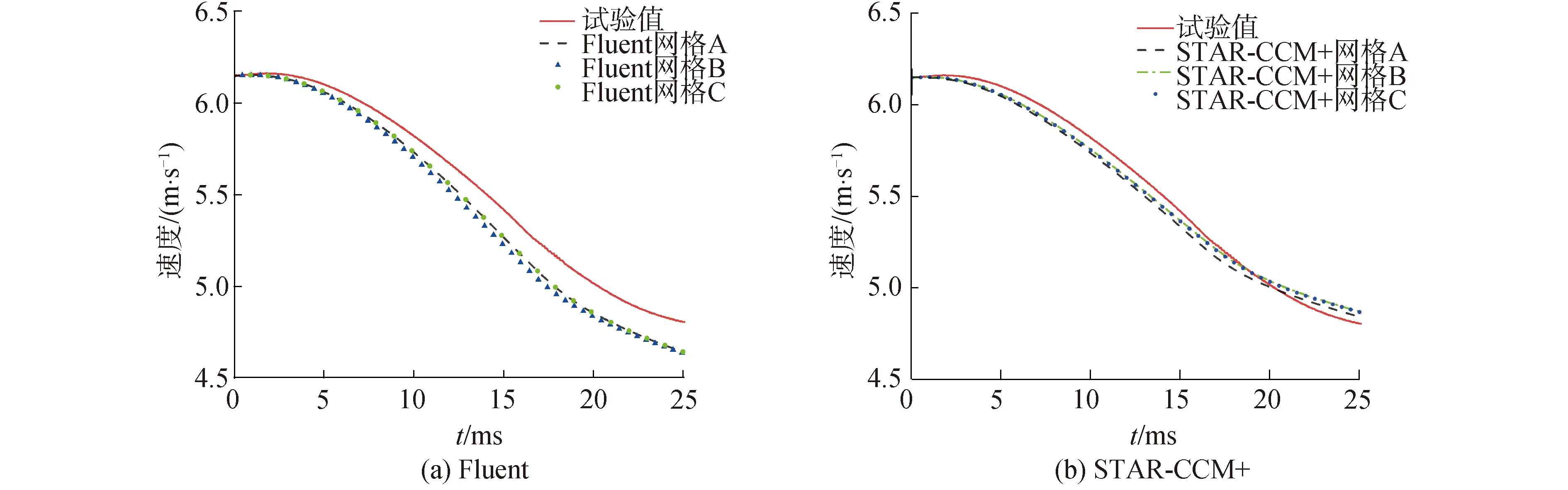
图4 速度变化曲线图Fig.4 Speed curve

由速度变化曲线可以看出，Fluent及STAR-CCM+中预报的速度变化趋势和试验结果整体上均趋势一致，证明本文所采用的2种CFD计算模型具有较好的可靠性。为了保障计算的精度，在接下来的模拟中，2种方法均选用较为精细的Mesh C网格。整体来看，STAR-CCM+的结果与试验更为接近。原因是在Fluent中的二维模型无法考虑到三维效应，而STAR-CCM+中考虑了三维效应，更接近试验的实际情况。但同时STAR-CCM+的网格数量也会远大于Fluent，致使计算量偏大。

为了更好地捕捉楔形体入水时的流场信息，2种计算模型均选取了较小时间步长0.000 1 s，均满足收敛性要求，在此不再赘述。

2.1.2 速度-压力耦合求解算法的选择

对速度和压力的耦合关系进行求解时，常用算法有SIMPLE、SIMPLEC、PISO和Coupled。在STAR-CCM+中采用的是默认的SIMPLE算法；在Fluent中为了对比计算精度，选择更为稳定的算法，分别采用不同算法进行模拟得到了砰击力曲线，并与STAR-CCM+及试验的结果进行对比，见图5。

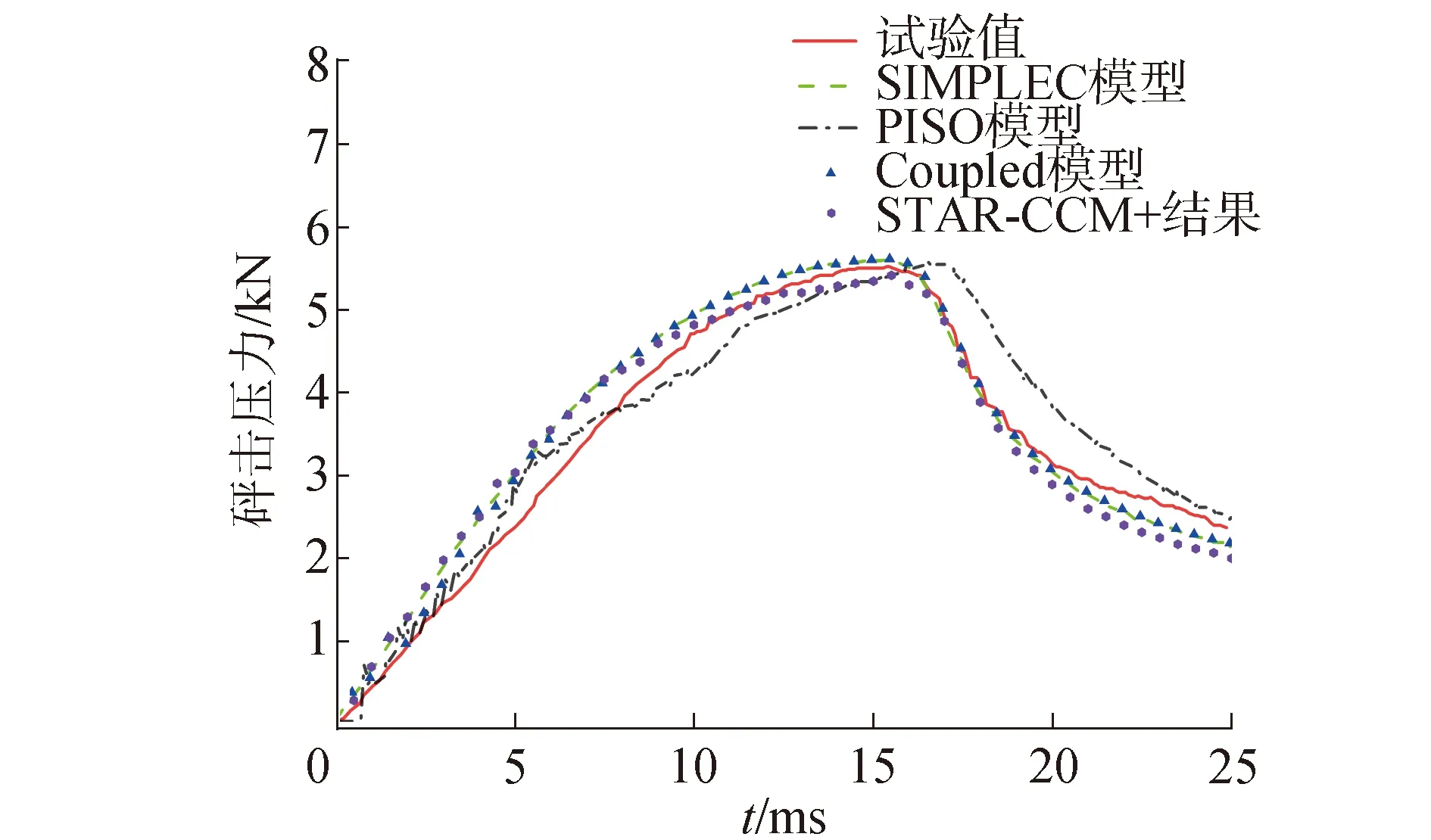
图5 各方法砰击压力结果比较Fig.5 Comparison of slamming pressure of each method

表4给出了数值计算和试验得到的砰击力峰值。结合图5与表4发现，在Fluent中，SIMPLEC算法和Coupled算法结果比较相近，但Coupled算法耗时较长，PISO算法虽然测得砰击力与试验误差最小，但计算结果较不稳定，因此在后续Fluent计算中采用SIMPLEC算法。

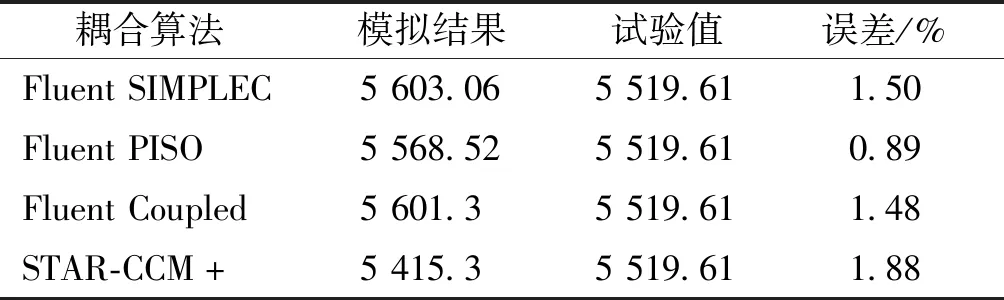
表4 数值结果与试验结果对比Table 4 Comparison of numerical and experimental results

整体来说，Fluent与STAR-CCM+中的计算结果均与试验值吻合较好，均具有较高精度；具体来看，STAR-CCM+计算结果要略小于Fluent，对于砰击压力极值的预报，STAR-CCM+误差略大.

2.1.3 测量点砰击压力曲线对比

按照Zhao等[7]的试验，设定楔形体的质量为241 kg，入水时刻速度为6.15 m/s，选择入水时刻为时间零点。根据上面2节的分析，Fluent中采用1.25 mm网格及SIMPLEC计算模型进行计算，在STAR-CCM+中采用基础尺寸60 mm网格进行模拟。对楔形体P1～P55个测量点处的砰击压强进行监测，图6是STAR-CCM+、Fluent计算结果以及试验结果的时历曲线图，仅展示P1、P3、P53个点。

从图6可见，2种计算模型所得各点数值结果均可实现自相互验证，且与试验结果吻合较好，展现出了相同的规律：测量点入水后所受砰击压力由0迅速增加到最大值，之后缓慢降低；随着各点入水深度的增加，砰击压力极值先增加后减少。相比来看，STAR-CCM+中各点砰击压力的极值结果略小于Fluent，但与试验值更为接近。图7为楔形体入水过程中2种计算模型的自由液面云图比较。

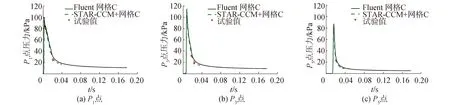
图6 各点砰击压力比较Fig.6 Comparison of every point slamming pressure

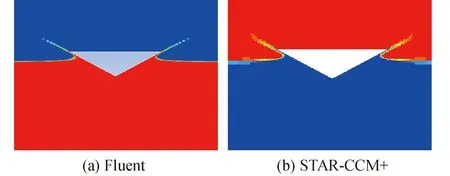
图7 入水自由液面云图对比Fig.7 Comparison of free surface cloud image

从图7可见，两者均能清楚地观察到液面上升以及射流时的液面分离现象。故为了简便，后续对于流场云图的分析将主要展示Fluent监测的结果。

综上所述，Fluent与STAR-CCM+对于楔形体入水问题的模拟结果较为接近，并与试验值吻合较好。由于STAR-CCM+中楔形体相比Fluent中纯二维情况多了一层厚度，更为接近真实情况。故STAR-CCM+结果与试验更为吻合，但同时其网格数较多，计算耗时长，需要根据实际情况进行选择。

2.2 速度对入水砰击的影响

2.2.1 入水速度对砰击压力的影响

设定楔形体的底升角为20°，质量为250 kg，分别以4、6、8、10 m/s速度入水。取楔形体尖端触水时刻为时间零点，监测楔形体从时间零点到完全入水过程中的各个参数变化情况。

图8给出了楔形体以4种不同速度入水时的砰击压力时历曲线。可得：STAR-CCM+与Fluent计算结果整体吻合较好，仅在极值点附近略有差别；STAR-CCM+得到的压力结果略低于Fluent结果。不同速度入水的楔形体砰击压力曲线呈现相同的趋势：在入水初期，随着入水深度的增加，砰击压力逐渐增加，在发生液面分离时砰击力达到最大值，之后缓慢降低。

随着入水速度增加，达到完全入水所需时间变短，砰击压力极值逐渐变大，出现砰击压力极值的时间也逐渐提前。入水速度为10 m/s的工况，其砰击压力极值远大于其他3种入水速度，这是由于入水初期，速度大的楔形体在表面形成的射流区域较大，沾湿面积也较大，产生的砰击压力极值也随之增大。

在楔形体右侧均匀布置P1～P44个压力测量点；P1、P2、P3、P4分别距离楔形体尖端53.2 mm、106.4 mm、159.6 mm、212.8 mm。监测楔形体在不同入水速度时砰击压力的变化情况，图9为STAR-CCM+与Fluent中的计算结果。在同一测点由于各速度下出现砰击力峰值的时间接近；为了易观察，采用曲线整体平移的方式：将4 m/s曲线整体向右平移0.015 s，6 m/s曲线向右平移0.01 s，8 m/s曲线向右平移0.005 s，10 m/s曲线保持不动。

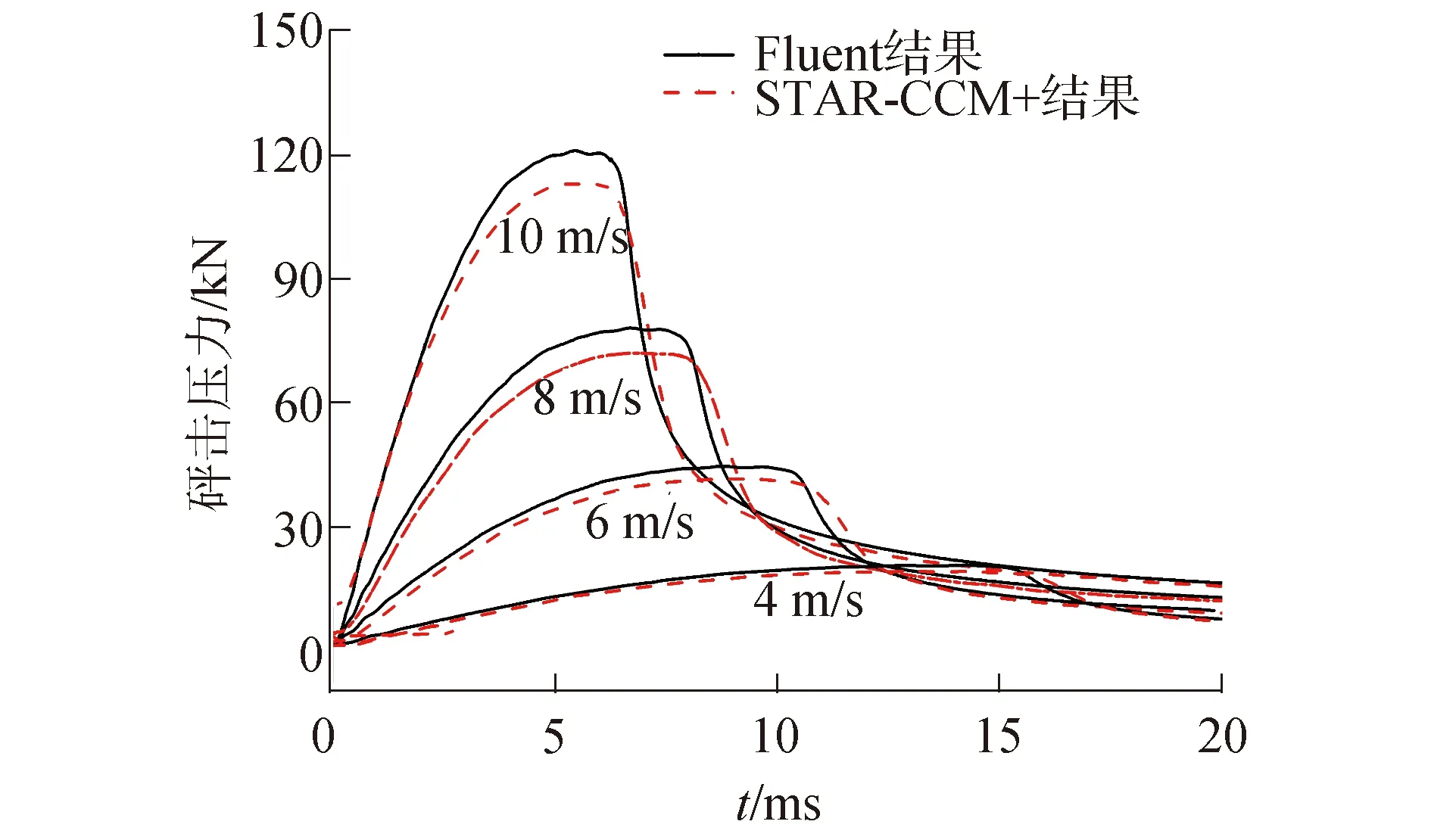
图8 砰击压力计算结果Fig.8 Calculation results of sniping pressure

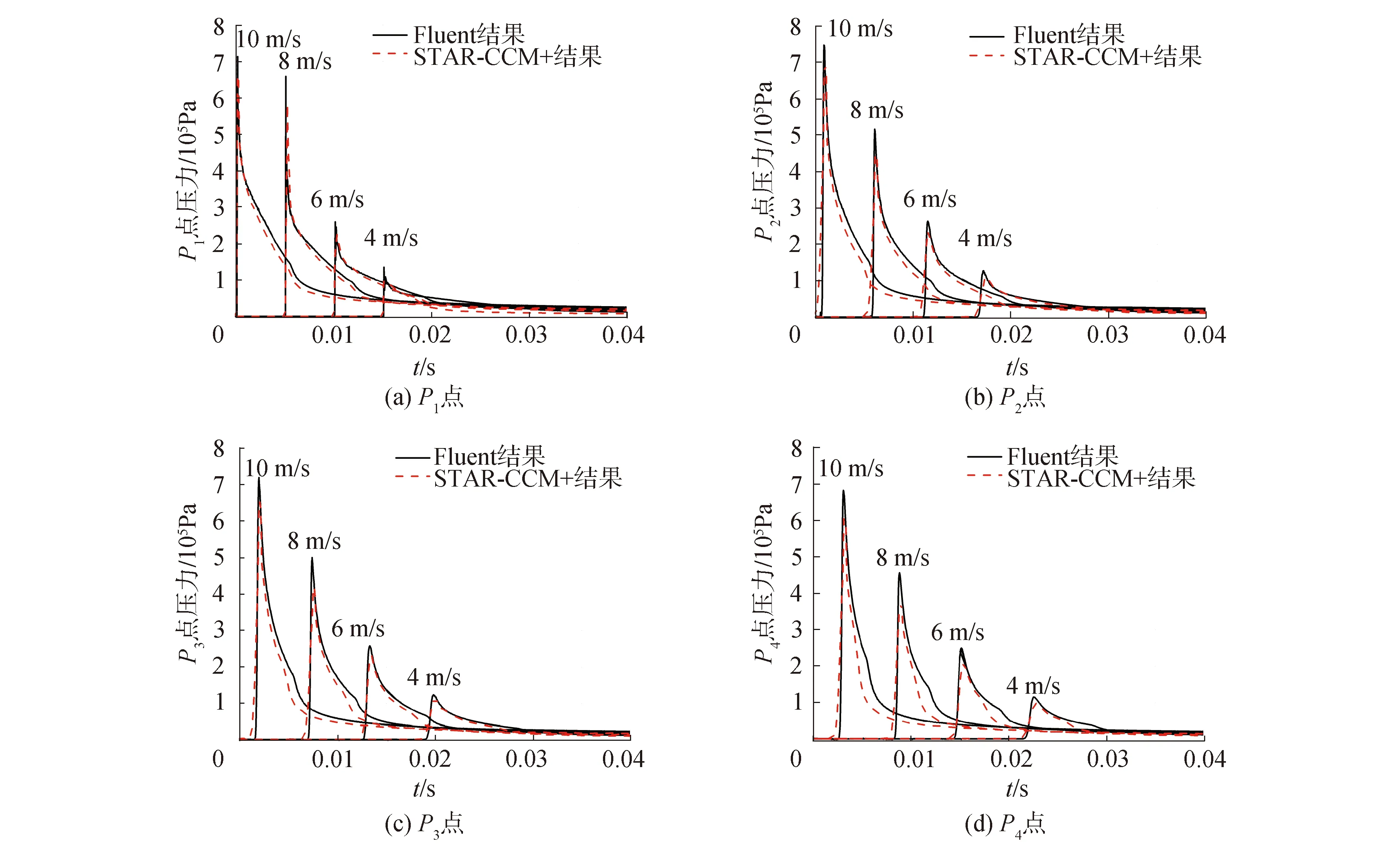
图9 各点砰击压力比较Fig.9 Comparison of sniper pressure at each point

由图9可以看出，两者展现出了相同的变化趋势，STAR-CCM+模拟得到的砰击压力极值略小于Fluent数值结果。随着入水速度增加，各监测点的砰击压力极值也随之增加；在同一入水速度下，P2、P3测量点处的砰击压力极值总是大于P1和P4测量点。说明楔形体入水时的最大砰击压力点出现在两侧中部区域，故在进行实际操作时需要对楔形体两侧中间区域进行材料加强处理。

2.2.2 入水速度对楔形体运动特性的影响

以楔形体尖端触水时刻为时间零点，楔形体完全入水时结束，图10给出了楔形体速度时历曲线。

由图10可见，2种数值模型计算结果吻合较好，展现了共性的变化规律：入水初期沾湿面积小，故阻力小，速度缓慢衰减；随着入水深度增加，阻力作用面积增大，砰击压力逐渐增长导致速度衰减加快；入水后期砰击压力减小又导致阻力减小，速度的衰减再次放缓，曲线出现拐点。STAR-CCM+的速度减少相对Fluent更加缓慢。楔形体入水速度越大，衰减速度越快，衰减幅度越大。结合图8可知，在入水初期，高速入水的楔形体会在较短的时间内产生巨大的砰击压力，且砰击压力极值远大于其他低速情况。因此入水速度越大，速度衰减幅度越大、速率越快，且由于楔形体入水速度较高时，砰击压力在峰值过后往往率先开始衰减，故导致阻力率先减小，相应的，曲线出现拐点的时间会提前。

图11为底升角20°楔形体以6 m/s入水时的相图。可以发现随着入水深度的增加，楔形体射流区域越来越明显，沾湿面积越来越大；到楔形体完全入水时液面飞溅形成水花。

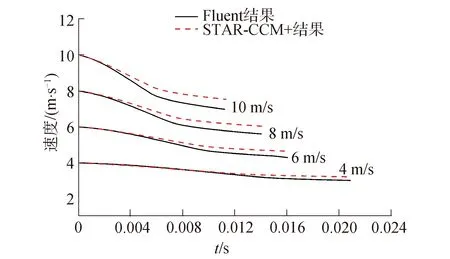
图10 速度变化趋势比较Fig.10 Comparison of speed trends

图11 底升角20°楔形体以6 m/s入水相图Fig.11 Phase diagram of 6 m/s with β=20°

2.3 楔形体底升角对入水砰击的影响

在进行船型设计研究时，需要确定船体剖面的载荷分布，故研究船体底升角变化对砰击压力的影响具有非常重要的意义。研究对象为底升角20°、30°和40°的楔形体，设定楔形体的质量为250 kg，保证入水时刻速度为10 m/s，监测楔形体由尖端触水到完全入水过程中的各参数变化情况。

2.3.1 底升角对砰击压力的影响

图12展了底升角为20°、30°和40°的楔形体受砰击力随时间变化曲线。从图12可知：不同底升角的砰击压力变化呈现相同的趋势。在入水初期，随着入水深度的增加，砰击压力逐渐增加；在发生液面分离以后，砰击力迅速降低，在液面分离时砰击力达到最大值。底升角越小，砰击压力极值越大，出现时间越早，这是由于小底升角楔形体在入水初期会产生较大的射流区域，使压力迅速增加。与前文一致的是，STAR-CCM+中的压力模拟结果略低于Fluent中模拟结果。

图13是不同底升角的楔形体在浸没时的相图。

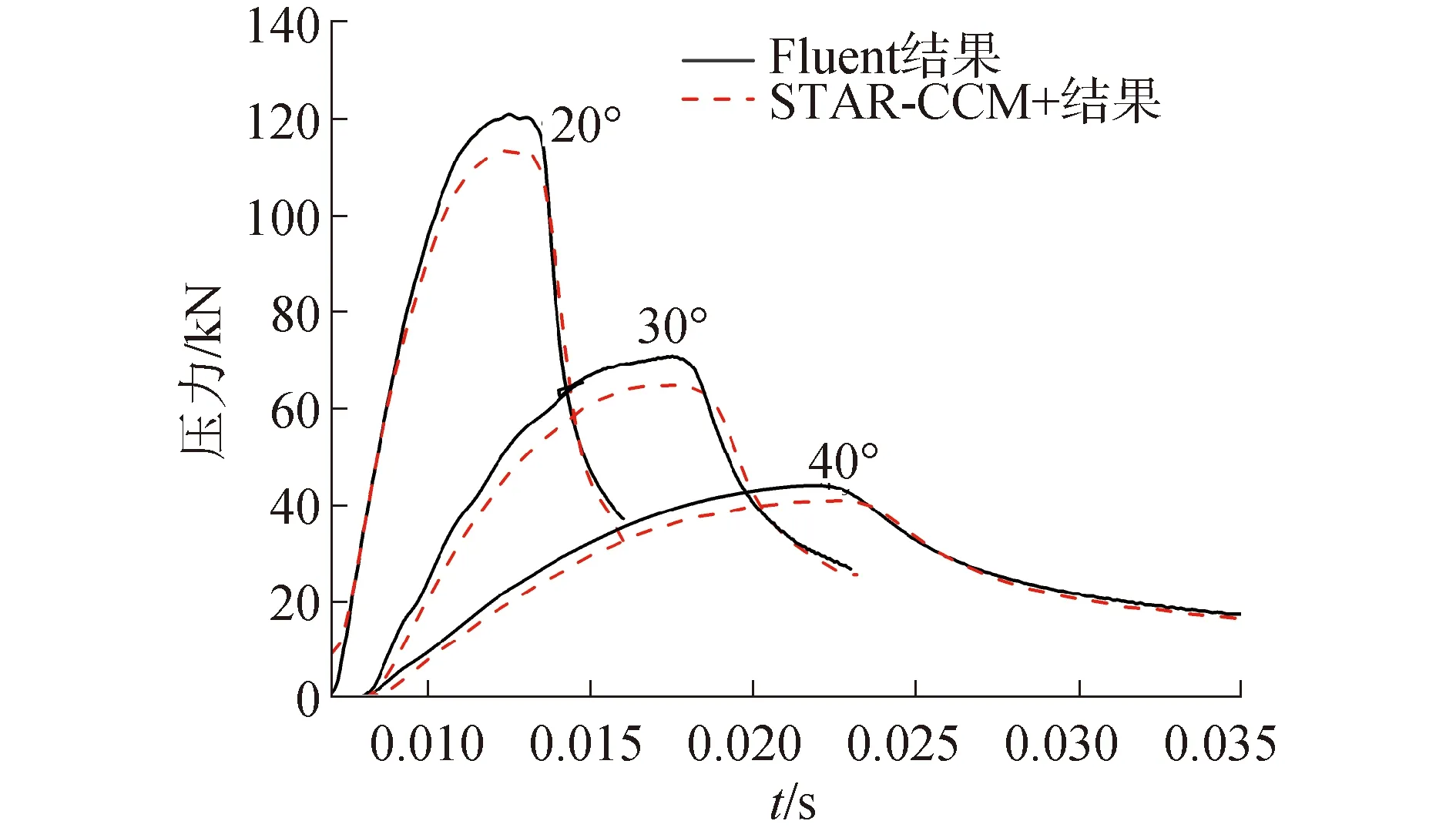
图12 不同底升角入水砰击压力的比较Fig.12 Comparison of the water pressure among three different bottom angle

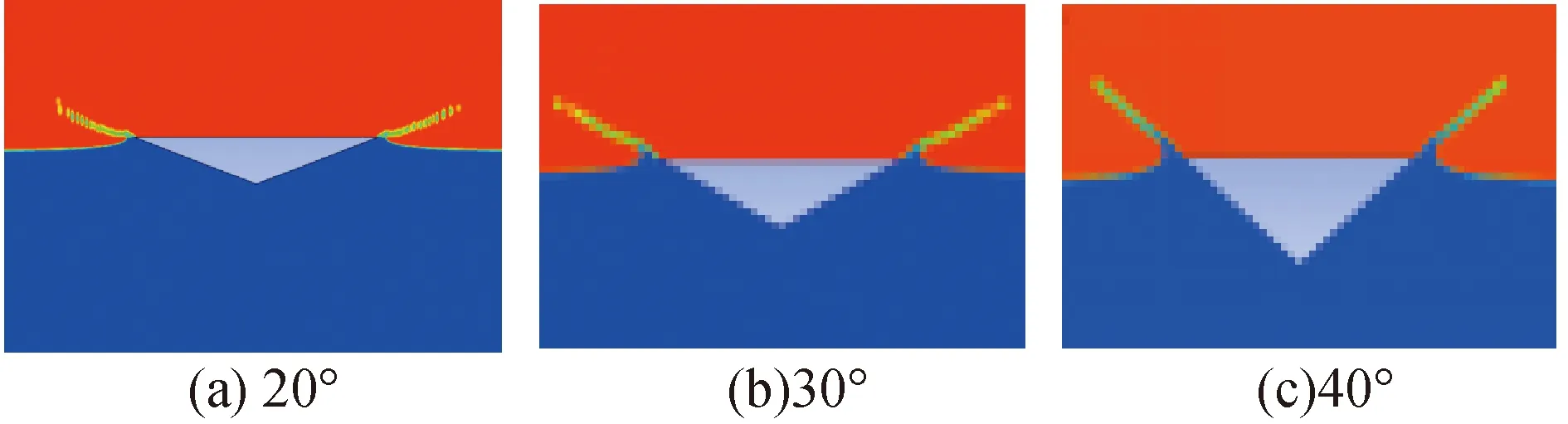
图13 不同底升角的楔形体入水相图Fig.13 Phase diagram of wedges at different bottom angles

从图13可以看出，底升角越小的楔形体，沾湿长度越长，产生的射流越明显。由于底升角小导致液面升高时液体所受挤压增加，在大气压力和重力等因素的共同作用下，砰击压力极值会增加。

为研究不同底升角时砰击压力极值分布规律，取3种底升角的楔形体在相同下落时刻(t=0.004 s)的砰击压力分布云图进行对比。如图14所示。可以发现，底升角越小，砰击压力极值的产生范围越小，这是由于射流在楔形体表面形成的角度变小而造成的。图15给出了底升角为20°的楔形体在入水t=0.004 s时刻的流场速度矢量图，可见气体在楔形体的边缘会形成漩涡，最大速度产生在喷射区，压力峰值出现在楔形体与自由液面接触区域。

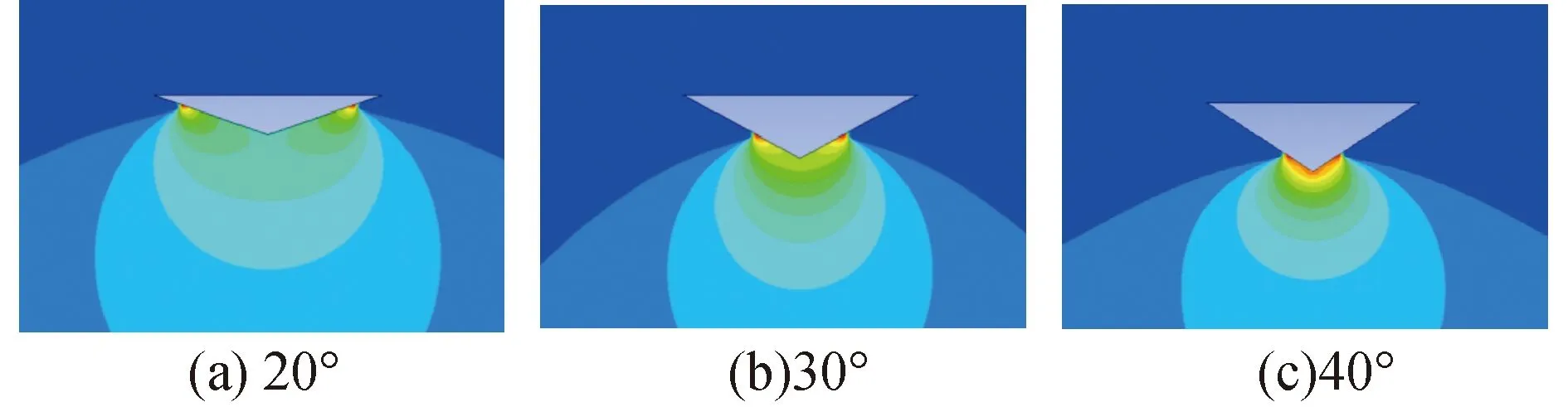
图14 楔形体压力云图Fig.14 Wedge pressure cloud diagram

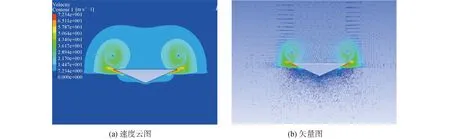
图15 底升角20°楔形体流场Fig.15 Flow field at 20° bottom angle

表5为t=0.004 s时刻下不同底升角楔形体的压力峰值。分析表5，在相同时刻下，不同底升角的楔形体压力峰值随底升角的增加而减小。

表5 在t=0.004 s时刻不同底升角的楔形体压力峰值Table 5 Peak pressure with different bottom angles at t=0.004 s

2.3.2 底升角对速度变化的影响

图16为速度变化曲线；可见，STAR-CCM+与Fluent趋势一致：入水初期，阻力小，速度减少缓慢；随着入水深度增加，砰击力加大，加速度增大，速度减少加快；之后砰击力又变小，速度衰减再次放缓. 比较各底升角的情况：底升角越小，入水时间越短，速度衰减越快。由于STAR-CCM+模拟结果中砰击压力略小，故速度衰减比Fluent缓慢。