基于改进粒子群算法的配电网无功优化

2020-02-07周璨董伟广钟建伟戴小剑田波龙玉雪

物联网技术 2020年1期

周璨董伟广钟建伟戴小剑田波龙玉雪

摘要：分布式电源的接入配电网有利于其无功优化、改善电压质量、降低网络损耗。以有功网损最小为其无功优化的目标函数，建立相应的数学模型，并对其进行仿真试验。由于基本粒子群算法的系数选择为常系数，存在人为选择系数过多依赖于经验的现象，具有一定的主观与偶然性，会导致粒子过于早熟，陷入局部最优。因此针对常系数粒子群算法的不足，将基于动态权值系数的改进型粒子群算法运用到无功优化中，对含有风、光等分布式电源接入的IEEE33系统模型进行仿真试验分析。试验结果表明，该算法能够有效降低网损，改善电压质量，提高系统的稳定性。

关键词：分布式电源;配电网;改进粒子群算法;动态权值系数;无功优化;迭代

中图分类号：TP39文献标识码：A文章编号：2095-1302（2020）01-00-03

0 引言

分布式电源的发展有利于缓解温室效应等全球性气候问题。它的接入可以调节负荷峰谷差，改善供电灵活性。配电网的无功优化是维护电力系统安全、稳定、改善电能质量的重要手段。与此同时，无功优化又是一个多约束条件的混合非线性规划问题。针对这种问题，以往常常采用牛顿法、非线性规划法和内点法等优化算法对其进行优化求解。

DG（Distributed Generation）的接入可通过调整输出无功功率的大小对系统进行无功优化，进而在一定程度上支撑系统各节点电压、减小网络损耗，确保系统稳定运行。针对无功优化问题，文献[1]提出了一种免疫PSO算法，可将其应用于新能源配电网无功多目标模糊优化。文献[2]主要研究考虑多个分布式电源接入配电网的多目标无功优化调度，将一种新的启发式算法—鲸鱼优化算法（WOA）运用到电网无功优化调度中。各种算法都有各自的局限性，如收敛时间长、对初值敏感、易过早成熟和陷入局部最优等。针对上述问题，本文提出了一种改进粒子群算法，通过引入动态权值系数对IEEE33系统模型进行优化求解。

1 无功优化模型

1.1 目标函数

本文的目标函数为有功网损，引入节点电压越界罚函数与动态权值系数来处理状态变量，建立最终的目标函数：

式中：Ploss为有功损网耗;n指系统中的负荷节点个数。

1.2 潮流方程约束

1.2.1 等式约束

节点有功、无功约束方程如下：

式中：i∈n，n指系统节点的总个数;PGi，QGi表示节点i注入的有功与无功;PLi，QLi表示节点i处负荷的有功与无功;Qci表示节点i的无功补偿量;Gij为电导;Bij为电纳;δij为电压相角差。

1.2.2 不等式约束条件

控制变量的不等式约束条件：

式中：VGi为发电机端电压;PDGi，QDGi为分布式电源的功率。状态变量的不等式约束条件可以表示为：

式中：QGi为发电机无功功率;VDi.max，VDi.min为节点i电压的上限与下限。

2 粒子群算法

2.1 基本粒子群算法

本文采用粒子群优化算法对多目标问题进行求解[3]。粒子群算法是受鸟类捕食这一现象的启发，将寻优问题看作鸟类寻找食物的问题，在空间初始化一些粒子（类比于鸟），然后粒子在空间进行搜索，每个粒子都知道自己距离最优点的位置与自己曾经走过的最优位置，基于粒子之间的位置共享，粒子按照一定的规则向最优粒子靠近，同时也受到自己走过最优位置的影响，在这种信息共享机制下，实现了粒子群寻优问题[4]。

粒子群算法中粒子之间的信息共享机制可以理解为一种共生合作的行为，并且每个粒子都将在给定的空间中不断搜索[5]，搜索机制既受自身搜索过程中最优路径的影响，也受群体之间信息位置的影响，在这样独特的搜索机制下，粒子不断向最优点靠近，最后完成寻优。粒子群算法首先生成初始种群，然后通过种群间粒子个体的合作与竞争来求解优化问题。

粒子群算法基本模型：D维空间，有N个粒子，第i个粒子表示D维空间的向量。

式中：Vi表示第i个粒子的速度;Xi表示第i个粒子的位置;Random（0，1）为在（0，1）内取的随机数。其速度更新的第一部分为粒子的记忆项，表示粒子会受上次速度位置的影响，这使得粒子保持一定的惯性，提高了全局寻优能力;第二部分称为自身认知项，体现出该算法中的动作来源于先前经验;第三部分为群体认知项，体现了粒子间的合作与知识共享[7]。

2.2 改进粒子群算法

惯性与学习系数决定了寻优性能的大小，惯性系数过大，粒子受之前位置的影响就会越大，使得粒子位置变化幅度变小，从而导致粒子全局寻优能力加强，但这也会导致寻优迭代收敛过慢。而社会学习与自我学习系数越大，粒子寻优能力就越強，但同时会导致粒子过于早熟，陷入局部最优。可见，系数的选择关乎寻优的成败，而传统的系数均为常系数，人为选择系数大多依赖于经验，具有一定的主观与偶然性。因此，针对常系数粒子群算法的不足，本文研究了基于动态权值系数的改进型粒子群算法。

改进型粒子群算法中，权值系数公式如下：

式中：w为惯性系数;t为当前迭代次数;c1与c2分别为自我与社会学习系数。

算法流程如图1所示。

基于动态权值系数的改进型粒子群算法程序的改进部分如下：

for t=1：Max_Dt

a（t）=x（1，1）;

for i=1：N

w=w_max-（w_max-w_min）*t/Max_Dt;//惯性权重更新

c1=（0.5-2.5）*t/Max_Dt+2.5;//自我学习

c2=（2.5-0.5）*t/Max_Dt+0.5;//社会学习

w=0.7;

c1=2.05;//自我学习系数

c2=2.05;//社会学习系数

v（i，：）=w*v（i，：）+c1*rand（）*

（y（i，：）-x（i，：））+c2*rand（）*（pg-x（i，：））;

for m=1：D

if（v（i，m）>v_max）

v（i，m）=v_max;

else if（v（i，m）<-v_max）

v（i，m）=-v_max;

end

如此，系数根据迭代次数线性变化，开始时，惯性系数w很大，使得全局寻优能力变强，随着迭代次数的增大，惯性系数慢慢变小，在获得多样性的基础上，使得粒子更多向最优粒子学習，增加收敛速度;同时，自我学习系数一开始也很大，使得粒子可以在更多区域进行搜索，增加粒子的多样性，避免粒子早熟，随着迭代次数的增加，社会学习系数逐步增大，使得粒子寻优收敛速度加快。

3 算例分析

在Matlab中编写程序，采用改进粒子群算法对IEEE33系统进行仿真测试。系统模型如图2所示。

系统节点1为平衡节点，风电发电方式为异步电机。本文将风电设为PQV节点进行处理，将光伏设为PQ节点进行后续处理。Max_Dt=100，搜索空间维数设定为D=50;粒子个数设为N=100;惯性权值的最大值设为w_max=0.9;惯性权值的最小值设为w_min=0.4;nummax=32;nummin=2;粒子速度v_max=2;系统中Ugmax=1.06，Ugmin=1.0;Vimax=1.1，Vimin=0.85。

采用改进粒子群算法对IEEE33系统模型进行无功优化的求解计算，得到优化前后的功率损耗、风电和光伏的出力情况、电压的改善情况以及优化后风电和光伏接入系统的最佳位置。优化前后单次总网损情况见表1所列。

通过表1可以得出，风、光等电源的接入具有一定的无功补偿功能。同时仿真试验结果表明，优化后其网损明显降低。

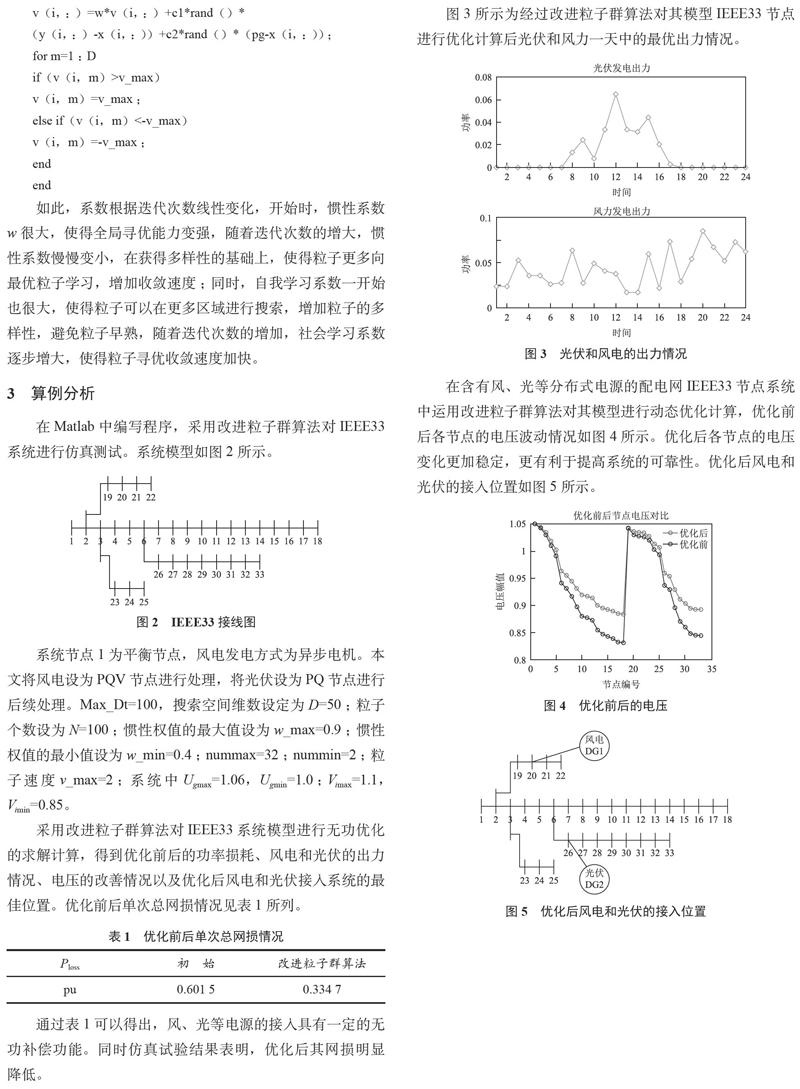
图3所示为经过改进粒子群算法对其模型IEEE33节点进行优化计算后光伏和风力一天中的最优出力情况。

在含有风、光等分布式电源的配电网IEEE33节点系统中运用改进粒子群算法对其模型进行动态优化计算，优化前后各节点的电压波动情况如图4所示。优化后各节点的电压变化更加稳定，更有利于提高系统的可靠性。优化后风电和光伏的接入位置如图5所示。

4 结语

运用改进粒子群算法对有风、光伏接入的IEEE33系统进行仿真分析：

（1）本文提出的改进粒子群算法针对常系数粒子群算法的不足进行了改进，进而研究了基于动态权值系数的改进型粒子群算法，解决了粒子过于早熟和易陷入局部最优的问题。

（2）本文提出的改进粒子群算法能够有效降低系统的有功网损，改善各节点的电压，有利于提高系统的可靠性。通过对IEEE33系统模型进行优化仿真试验，得出了光伏和风力接入系统的最优位置和一天中风力和光伏的最优出力情况，有效解决了无功优化问题。

参考文献

[1]司徒友，吴杰康，郭清元，等.基于免疫PSO的新能源配电网无功多目标模糊优化[J].中国电力，2018，51（2）：90-98.

[2]滕德云，滕欢，刘鑫，等.考虑多个分布式电源接入配电网的多目标无功优化调度[J].电测与仪表，2019，56（13）：39-44.

[3]强国栋，高锋阳，乔垚，等.基于改进粒子群算法的配电网无功优化[J].电测与仪表，2018，55（14）：21-26.