纤维红黏土强度的正交试验及多元非线性回归分析
2020-02-07陈佳雨刘之葵陈永国席丹妮
陈佳雨,刘之葵,陈永国,席丹妮
(1.桂林理工大学土木与建筑工程学院, 广西 桂林 541004; 2.广西岩土力学与工程重点实验室, 广西 桂林 541004)
桂林地区红黏土分布广泛,红黏土具有高含水率、低密度、压缩性较低等特性,其自身特点决定了其不适合作为路基填筑材料,需对其进行改良加固处理[1]。针对桂林红黏土的加固改良,许多学者进行了相关研究。已有研究表明随水泥掺量的增大,水泥加固红黏土的无侧限抗压强度增大趋势逐渐减缓[2-3]。还有研究者[4-5]发现水泥红黏土抗剪强度指标c,φ随着水泥掺量的增加而增大。粉煤灰及二灰的掺入也会提高红黏土抗剪强度[6]。纳米石墨粉可有效提高红黏土黏聚力,对内摩擦角影响不大[7]。目前关于桂林红黏土的加固改良的研究主要集中于化学方法加固方面,化学添加剂虽然能明显提高土体的性能,却会使土壤具有高硬度和脆性,而物理方法加固可弥补这一缺陷。但目前对桂林红黏土进行物理加固改良的研究还未见报道。
纤维加筋是常用的土体物理加固改良方法,纤维加筋技术是指在土体中随机均匀加入纤维,使纤维与土颗粒有效接触,在破坏面上纤维可发挥其抗拉能力,阻止破坏面发展,从而提高土体的抗剪强度[8],因其具有成本低、易施工和环保的特点,被广泛应用于铁路、公路的路基、边坡、大坝和河岸工程中。近年来国内外学者对不同纤维加筋土的强度特性进行了一系列研究。唐朝生等[9]研究发现,聚丙烯纤维加筋砂土的黏聚力随含砂量的增加先增大后减少,内摩擦角大小与掺砂量成正比。聚丙烯纤维掺入黄土后,土体应变特性从软化型转变为应变硬化型,极大的提高了黄土的韧性,有利于增强其抵抗大变形的能力[10]。稻秸秆加筋可以有效减少土体裂缝的产生,在加筋率为0.3%时,抗裂性能最优[11]。在高孔隙率、低强度和高压缩性软土中掺入剑麻纤维能显著提高其抗剪强度参数[12]。以往研究表明纤维加筋土的强度特性受纤维长度、纤维掺量的影响:膨胀土的c,φ随纤维含量的增加先增大后减小[13]。剑麻纤维加筋黏性土时,短纤维对提高无侧限抗压强度的效果要好于长纤维[14]。赵宁雨等[15]通过三轴试验发现,聚丙烯加筋红黏土合理的加筋纤维长度在 10~13 mm。还有研究发现干密度和含水率的变化也会引起纤维加筋土强度特性的改变,在最优含水率和最大干密度下,加筋土的抗压强度和抗剪强度较高,加筋效果最优[16]。
综上所述,纤维加筋土的强度特性与纤维长度、纤维掺量、含水率及干密度等多因素相关,但现有的研究集中于对单因素或双因素作用下纤维加筋土强度变化规律的总结,考虑多因素耦合作用对纤维加筋土的影响及其显著性鲜有报道。
针对桂林红黏土物理加固改良理论研究的空白及纤维加筋土现有研究理论的不足,以桂林红黏土抗剪强度指标c,φ为研究对象,选取应用广泛的聚丙烯纤维为改良材料,采用正交试验设计方法,研究纤维长度-纤维掺量-含水率-干密度多因素耦合作用下纤维加筋红黏土的抗剪强度特性,对试验结果进行极差、方差分析,从而确定最优制备工艺组合及各个因素对c,φ的影响大小,并运用SPSS统计软件建立多因素与纤维加筋红黏土c,φ的数学关系模型,揭示多个因素与纤维加筋红黏土c,φ之间的关系,以期为该地区相关地基、路基设计工程提供理论依据。
1 正交试验
1.1 试验材料
试验用土取自桂林市雁山区某施工场地,其物理力学性质指标如表1所示。选取的聚丙烯纤维(以下简称为纤维)物理力学参数如表2所示。

表1 红黏土物理力学性质

表2 聚丙烯纤维物理力学参数
1.2 正交试验设计
正交试验设计(Orthognal experimental design)是研究多因素多水平的一种设计方法,它可以在不影响全面掌握诸多因素对性能指标影响的条件下,大大减少试验次数,是一种高效率、快速、经济的试验设计方法。本文正交试验选取强度指标黏聚力、内摩擦角(以下均用c,φ表示)作为试验的考核指标,纤维掺量、纤维长度、含水率、干密度为影响因素,建立4水平4因素L16(45))正交试验表,因素水平设计见表3。
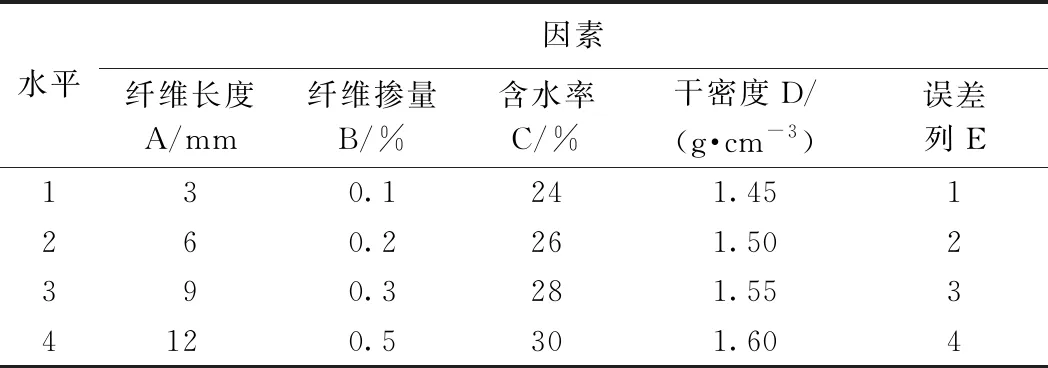
表3 因素水平表
1.3 试验方法
将取回的红黏土风干后碾碎,过2 mm筛备用。取适量土样烘干后,按表3中设计的各因素水平指标计算并称取所需干土的质量、水、纤维的质量。为避免土样太干燥导致纤维之间出现抱团现象,制样时先洒入适量的水分,使土样具有一定湿度后再将纤维分层并均匀地撒入土中,最后洒入剩余水分配制到表3中的目标含水率。将配制好的土样装入塑料袋中静置24 h,待水分迁移平衡后,称取适量湿土倒入环刀(61.8 mm×20 mm)中压实土样,每组土样压制4个土样。试验仪器采用的是南京土壤仪器厂生产的 ZJ 型应变控制式四联直剪仪,分别施加100,200,300,400 kPa垂直压力,根据《土工试验方法标准》[17],取应变位移为6 mm作为试验结束指标,剪切速率均采用0.8 mm/min。
2 试验结果及分析
对表3中各组纤维红黏土(以下简称为纤维土)试样进行直剪试验,试验结果见表4。
2.1 试验结果的极差分析
基于表4的试验结果,对不同因素作用下纤维土的c,φ进行极差分析,分析结果见表5。
表中Ki(i=1,2,3,4)表示某个因素第i个水平的所有考核指标数值之和,i为影响因素的水平数。ki表示其对水平数的均值,即ki=Ki/4;ki值的大小可判断某因素的最优水平,最大的ki值对应的水平为最优水平。R为某种因素的ki最大值与最小值之差,即极差,R值越大,则该因素对考核指标的影响越明显。
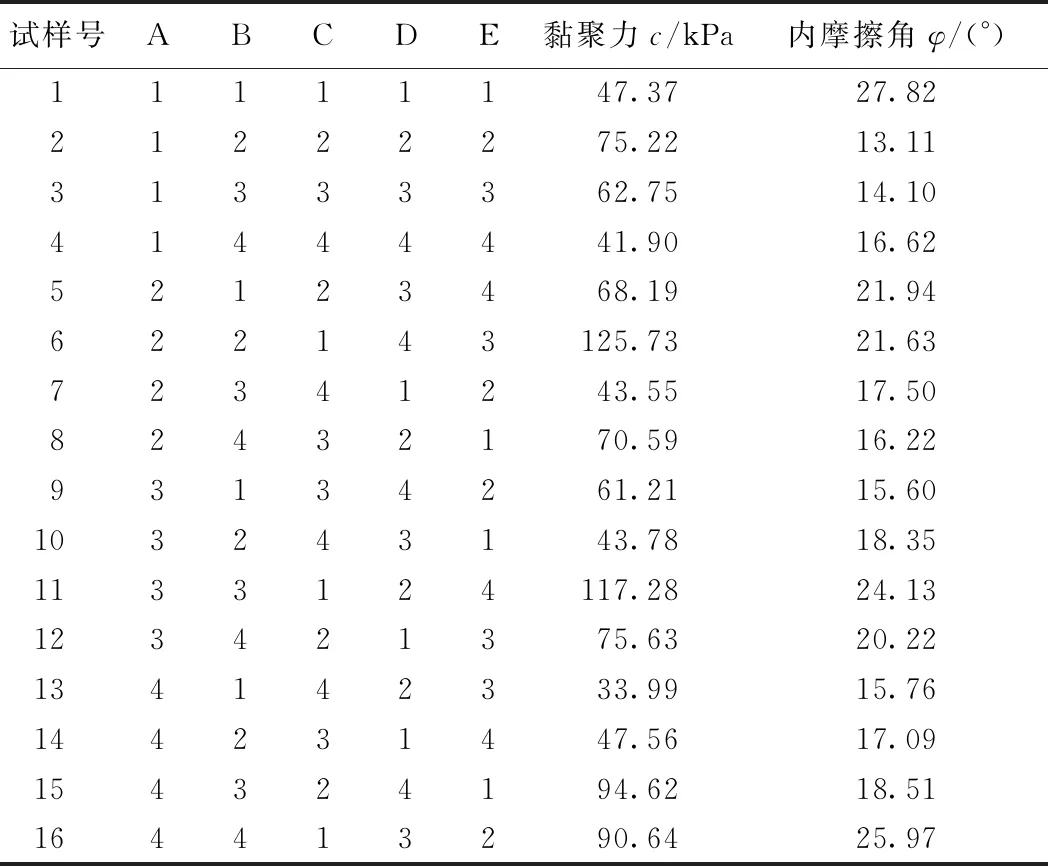
表4 正交试验结果
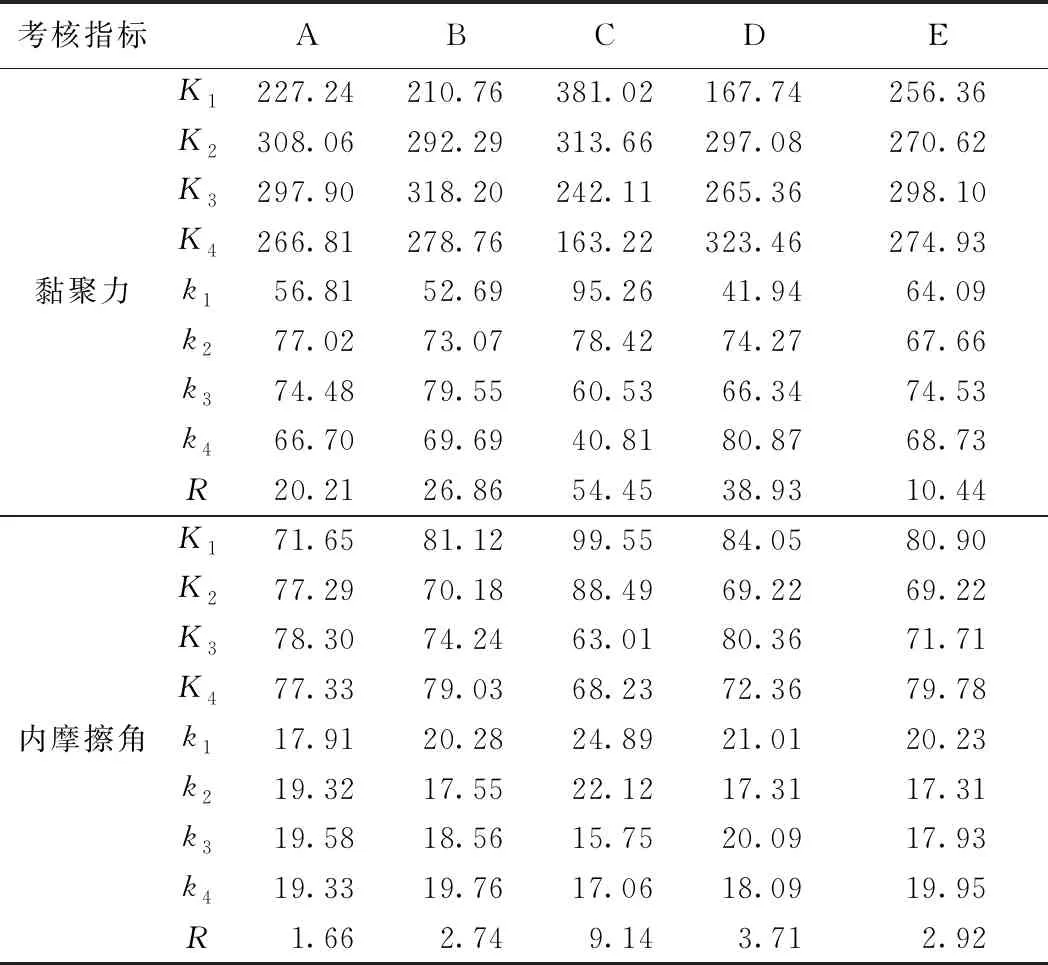
表5 正交试验的极差分析结果
2.1.1黏聚力的极差分析
通过对表5中各项因素的黏聚力的R值比较可知:RC>RD>RB>RA,即试验中4个因素对纤维土的c的影响主次顺序依次为:含水率>干密度>纤维掺量>纤维长度。对比ki值发现:A水平因素作用下,k2>k3>k4>k1,说明A因素在第2水平时,纤维土c取得最大值。同理可得B,C,D各因素的最优水平分别为第3水平、第1水平、第4水平。因此在考虑因素单独作用的条件下,当水平组合为A2B3C1D4时,即纤维长度为6 mm、纤维掺量为0.3%、含水率为24%、干密度为1.6 g·cm-3时纤维土的黏聚力最高,说明此水平组合为提高纤维土c的最优制备工艺组合。
2.1.2内摩擦角的极差分析
表5中各项因素的内摩擦角R值大小为:RC>RD>RB>RA,可知试验中4个因素对纤维土内摩擦角影响主次顺序依次为:含水率>干密度>纤维掺量>纤维长度。A水平因素作用下,k3>k4>k2>k1,表明A因素在第3水平时,φ取得最大值。同理可得B,C,D各因素的最优水平均为第1水平。在考虑因素单独作用的条件下,纤维土φ的最优制备工艺组合为A3B1C1D1时,即纤维长度为9 mm、纤维掺量为0.1%、含水率为24%、干密度为1.45 g·cm-3时纤维土的φ最高。
2.2 试验结果的方差分析
极差法直观地分析了各因素对强度影响大小顺序,但是并不能精确估计试验过程中因素水平与试验误差对试验结果影响的重要程度,且没有把试验过程中由于试验条件的改变所引起的数据波动与试验误差所引起的数据波动区分开来[18]。针对极差分析方法中的不足,引入方差分析方法对纤维土抗剪强度指标试验数据进行处理,并对计算结果进行分析讨论。对不同因素作用下纤维土的黏聚力、内摩擦角进行方差分析,结果见表6。
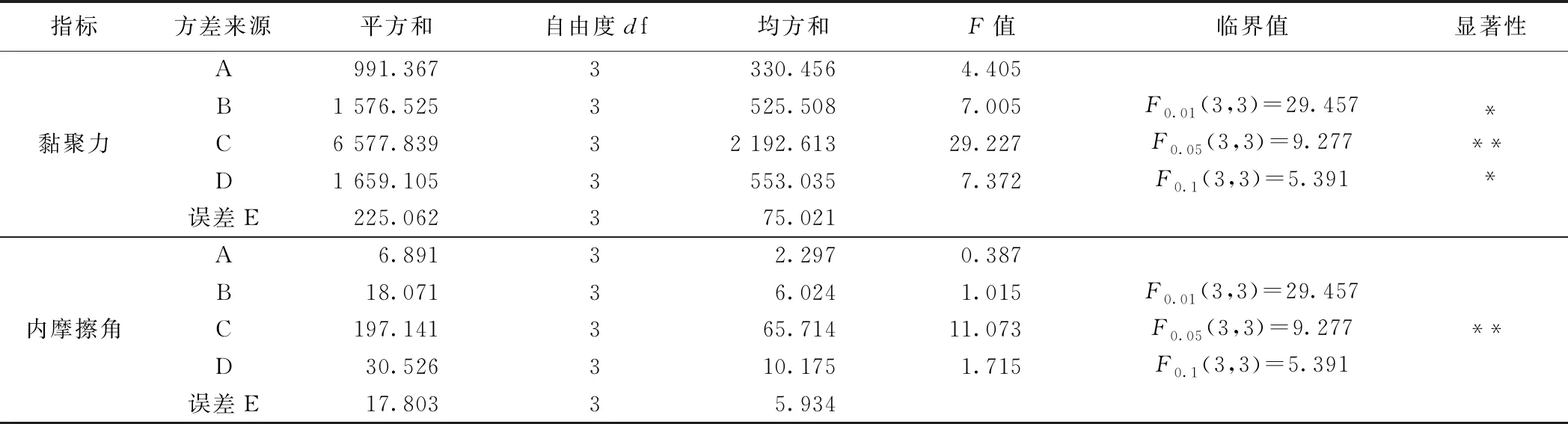
表6 正交试验的方差分析结果
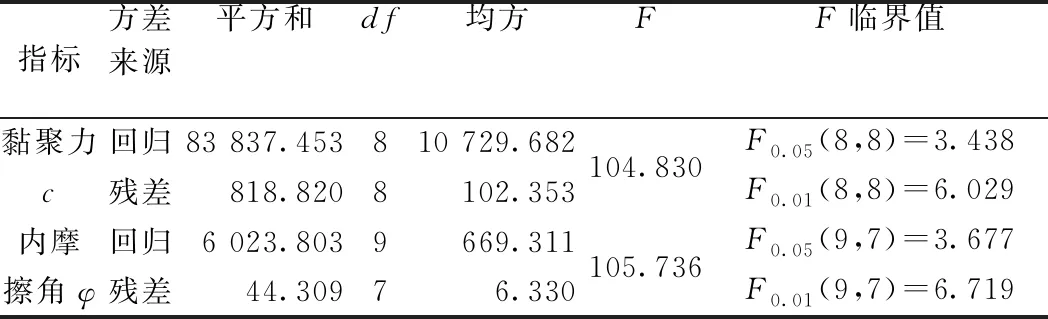
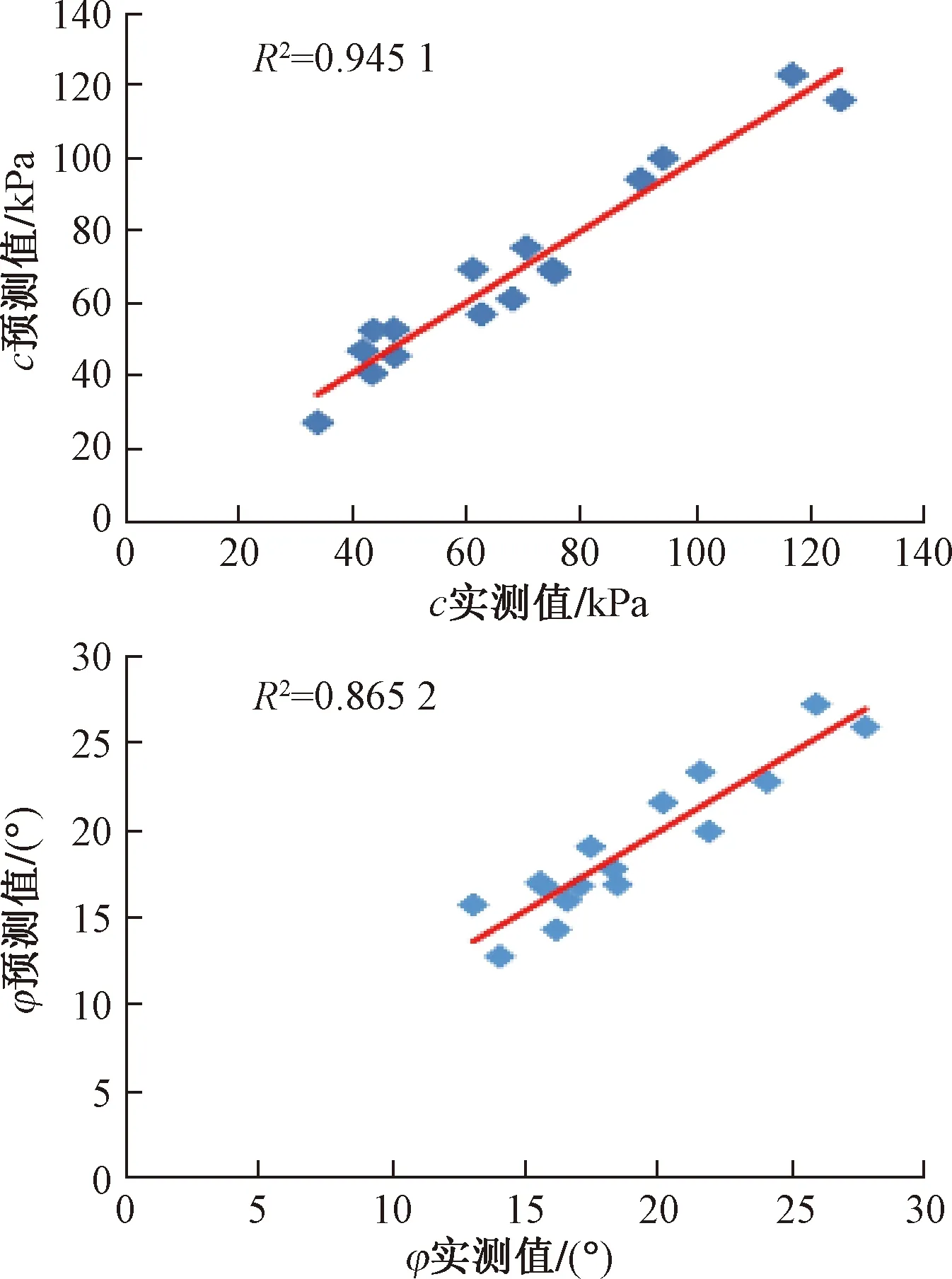
给定判定标准:当Fi>F0.01(3,3)时,则表示影响非常显著,用*** 表示;当F0.01(3,3)>Fi>F0.05(3,3)时,则表示影响显著,用** 表示 ;当F0.05(3,3)>Fi>F0. 1(3,3)时,则表示有一定影响,用 * 表示 ;当Fi 由表7可知:各因素c的F值明显大于φ,表明各因素水平的改变对c的产生影响大于对φ的影响。对于c而言,F0.01(3,3)>FA>F0.05(3,3),表明含水率对c的影响显著;F0.05(3,3)>FB、FC>F0. 1(3,3),表明纤维掺量与干密度对c有一定的影响;而对于φ而言,仅FA>F0.05(3,3)=9.277,可见仅含水率对纤维土的φ产生显著影响,其余各影响因素对纤维土φ无显著影响。 根据极差分析结果,以每个因素的ki值为纵坐标,横坐标用不同因素的水平表示,绘制各因素对纤维土c,φ的影响趋势曲线(图 1)。 (1)从图1可知:c随纤维长度的增大呈现增大后减小的趋势,峰值出现在6 mm时。这是由于纤维长度较小时,单根纤维与土体的摩擦面积较小,纤维增强方式主要以一维拉筋作用为主。随着纤维长度的增大,纤维之间会发生交互现象,形成三维网状结构,增强传力效果,且纤维的锚固长度增大,不易被拉断,因此c不断增大。但纤维过长时易缠绕成团,且锚固长度过大,不利于纤维拉伸作用的发挥从而弱化了传力效果,造成c下降。 图1 各因素对c,φ的影响趋势Fig.1 Trend diagram of the influence of different factors on c and φ φ随着纤维长度的增大呈现出先升高后降低的变化规律,整体上变化幅度不明显,在纤维长度为9 mm时取得最大值。主要因为纤维表面平整光滑,掺入土中后对土颗粒的粗糙程度不产生影响,仅对土颗粒的咬合程度会产生影响。较短的纤维在土中排列易与剪切方向平行,对土颗粒无约束作用,随着纤维长度增大,纤维在土中会发生弯曲,纤维弯曲部位会限制土颗粒的移动,增强了颗粒与颗粒之间的咬合摩擦,引起φ增大。但纤维过长时因抱团程度明显,弱化了许多纤维团的内部纤维对土颗粒的约束作用,导致φ降低。 (2)c随纤维掺量的增大呈现出先升高后降低的变化规律,当纤维掺量为0.3%时出现拐点,说明在纤维掺量为0.3%时,c达到最大值。主要原因是纤维掺量的不同会影响纤维的主要增强方式。当纤维掺量较低时,纤维在土中分布离散无法形成纤维网,c的贡献基本来自离散纤维的一维拉筋作用。而随着纤维掺量的增加,纤维之间开始交织成网,此时纤维对c的贡献还增加了三维拉筋作用,导致c增大。但纤维掺量继续增加后,纤维相互间定向平行排列的机会增大,不仅会弱化了三维空间网状结构传力作用,还会在土体中形成受力的软弱区,降低土体的强度,表现为c减小。 φ随着纤维掺量的增大呈先降低后升高的变化趋势,下降趋势明显大于上升趋势,但整体变化幅度仍然较小;当纤维掺量为0.1%时取得最大值。究其原因为:纤维掺量较少时,纤维的掺入可以填充一部分土体孔隙,使土体更密实,增强了土颗粒间的咬合摩擦,表现为φ较大。随着纤维掺量的增大,土颗粒间的接触被部分纤维与颗粒、纤维与纤维间的接触逐渐代替,由于纤维表面比土颗粒光滑,使得土体的咬合摩擦系数减小,宏观表现为φ减小。但随着掺量的持续增大,纤维土中的三维空间网状结构增强,增强了颗粒与颗粒间的咬合摩擦,引起φ增大。 (3)c随着含水率的增大呈近似线性降低趋势,当含水率为24%时,c是含水率为30%时的2.33倍。含水率的增加从以下两个方面弱化了c:一是含水率的增大,纤维-土界面的自由水分子增多,纤维与土之间易于发生滑动,不利于纤维与土的接触粘结;二是根据双电层理论,含水率增大后距土粒表面一定距离的水中离子浓度减小,使得扩散层厚度增大,电动电位提高,进而引起胶粒分散,土颗粒间的胶结作用减弱。因此随着含水率增大,c呈下降趋势。 φ随着含水率的增大整体下降趋势非常明显,说明含水率的大小对φ影响很大,当含水率为24%时,φ达到最大值。这是因为含水率的增大,土中水分子增多,润滑作用增强,纤维-土界面的摩擦系数减小,从而φ减小。 (4)c随着干密度的增大呈先升高后降低再升高的变化规律,且上升幅度大于下降幅度,使整体呈上升趋势,分别在干密度为1.45 g·cm-3、1.6 g·cm-3时取得最小、大值。分析其原因认为:干密度增大使土颗粒含量增多,颗粒间接触点增多,使分子间的引力增大,表现为c增大。φ随着干密度的增大整体无明显变化规律,此时干密度的增大对纤维土的强度增强主要体现在黏聚力的提高。 由图1可知,各因素与纤维土c、φ的关系是非线性的,故需采用多元非线性回归模型表示它们之间的函数关系。多元非线性回归模型是指一个因变量受多个自变量影响而且呈现非线性关系的模型,可先分别建立各因素与强度指标的最优一元非线性回归模型,再运用SPSS软件将考核指标对各因素的最优一元回归非线性模型进行多元线性回归,从而建立各因素与考核指标的多元非线性回归模型[19]。 根据图1采用SPSS软件对各因素与强度指标进行曲线估计,经过曲线估计建立纤维长度与c的最佳一元二次曲线模型为: c1=-0.7772x12+12.562x1+26.994 (1) 同理可得纤维掺量与c的二次曲线关系式为: c2=-480.48x22+329.07x2+25.103 (2) 同上,建立含水率与c的最佳函数方程为: c3=-9.0619x3+182.99 (3) 干密度与c对应的函数关系为: c4=-1781x42+5649.8x4-4402.5 (4) 根据公式(1)~(4),可建立c的多元非线性回归模型如下: (5) 式中:βj——待定多项式系数; cn——各因素与c的最优一元非线性模型; j,n——待定系数个数、最佳一元非线性模型个数。 采用SPSS统计软件对c进行多元线性回归,得到多因素与c的多元非线性回归模型为: c=-6.616+37.686x1-6.994x12+43.551x2- 7.561x22-18.124x3+15.180x4-1.554x42 (6) 同理可建立各因素与φ的最佳一元非线性曲线模型分别为: φ1=-0.0459x12+0.839x1+15.842 (7) φ2=50.199x22-30.327x2+22.481 (8) φ3=0.2544x32-15.229x3+244.43 (9) φ4=170.75x42-532.75x4+433.97 (10) 根据公式(7)~(10),可建立φ的多元非线性回归模型如下: (11) 式中:αj——待定多项式系数; φn——各因素与φ的最佳一元非线性模型; j,n——待定系数个数、最佳一元非线性模型个数。 采用SPSS统计软件对φ进行多元线性回归,得到各因素与φ的多元非线性回归模型为: φ=40.046+2.517x1-0.413x12-4.971x2+ (12) 3.3.1相关性检验 根据多元非线性回归的检验方法,对回归方程进行相关性检验。相关性表示自变量与因变量的线性关系,可以用相关系数R来表示他们之间的密切程度: (13) 式中:xi,yi——2个变量序列; 当|R|越接近1,表示自变量与因变量关系越密切,拟合效果越好。通过回归分析,得出c的非线性模型的相关系数为0.972,φ的非线性模型的相关系数为0.930,均接近1。因此,可以确定该模型的拟合效果极佳。 3.3.2显著性检验 F检验法为常见的线性回归显著性检验方法,通过给定显著水平β(β常取0.01或0.05),回归计算得出F的数值,若F≥Fβ(p,n-p-1),则认为线性回归显著(其中p为自由度,n为样本数)。对c,φ的多元非线性回归模型进行显著性分析,结果如表7。 表7 多元非线性回归模型显著性分析结果表 从表7可知,经计算得到c的回归模型的F值为104.83,远大于F0.01(8,8)=6.029,可以确定线性回归显著;φ的回归模型的F值为105.736,远大于F0.01(9,7)=6.719,也可确定线性回归显著。可见,c、φ的多元非线性回归模型能够精确地反映4个影响因素与强度指标之间的关系。 3.3.3拟合分析 为进一步判定多元非线性回归模型的准确性,将根据c,φ多元线性回归模型拟合出的预测值与实际值进行对比(图2)。 图2 强度指标实测值与预测值拟合结果Fig.2 Fitting results of the measured and predicted values of the strength indicators 从图2可看出:由多元线性回归模型拟合出的强度指标预测值与实际值大小相近,紧密分布在拟合线两侧,线性关系十分明显。c,φ的实际值与预测值的拟合曲线判定系数分别为0.972,0.927,表明c,φ的预测值与实际值拟合度高。 综上所述,c,φ的多元非线性回归模型预测精准,可靠性强,能为该地区对多因素耦合作用下c,φ的预测提供一种快捷、可靠的方法,具有一定的工程应用价值。 (1)各因素对纤维土抗剪强度指标c,φ的影响主次顺序均为:含水率>干密度>纤维掺量>纤维长度;纤维土c的最优水平组合为: A2B3C1D4,即纤维长度为6 mm、纤维掺量为0.3%、含水率为24%、干密度为1.6 g·cm-3时纤维土的c最高;纤维土φ的最优水平组合为: A3B1C1D1,即纤维长度为9 mm、纤维掺量为0.1%、含水率为24%、干密度为1.45 g·cm-3时纤维土的φ最大。 (2)各因素水平的改变对c的影响大于对φ的影响;含水率对c的影响显著,纤维掺量与干密度对c有一定的影响,纤维长度对c无明显影响;含水率对纤维土的φ产生显著影响,其余各影响因素对纤维土φ无明显影响。 (3)c,φ的多元非线性回归模型的判定系数较高、回归显著且拟合度高,即回归模型具有较高准确性,可靠性强,能精准的表达多因素与c,φ的函数关系,可将其应用于相关纤维红黏土地基的设计工程中。2.3 试验结果的机理分析
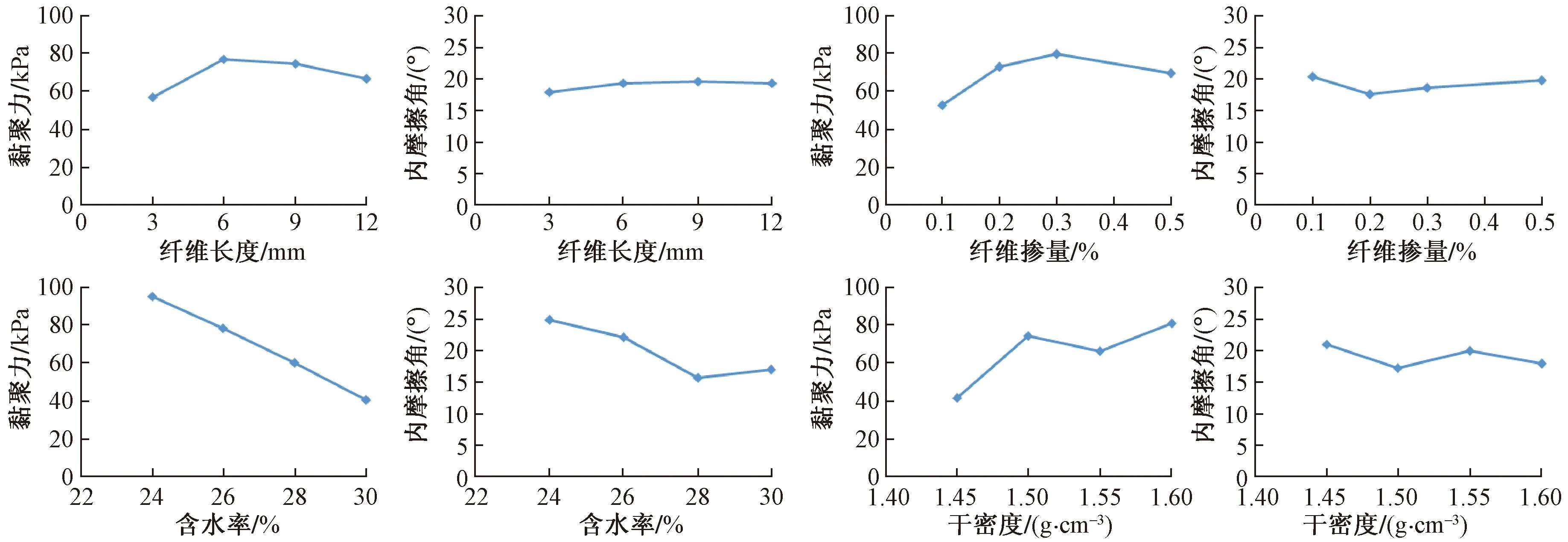
3 纤维土强度与各因素多元非线性回归分析
3.1 黏聚力的非线性回归模型的建立
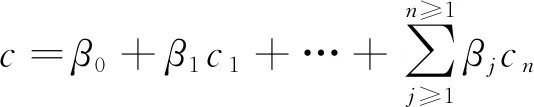
3.2 内摩擦角的多元非线性回归模型的建立
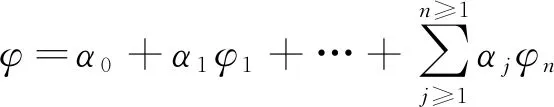
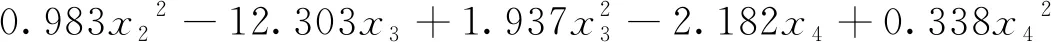
3.3 回归模型的验证
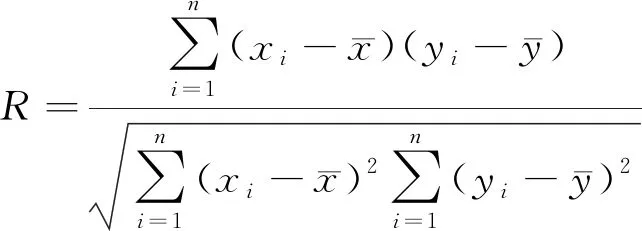
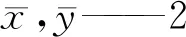
4 结论
