基于连续混合正态分布的期货定价偏差研究

宋玉平，陈志兰

(上海师范大学 商学院，上海 200234)

一、引 言

股指期货是一种发展迅速的金融衍生产品，它具有对冲风险、套期保值以及活跃市场等作用，准确的股指期货定价对交易者来说具有十分重要的意义。Cornell等最早提出了无税收、无交易成本和无卖空限制等完美条件下的股指期货持有成本定价模型[1]。现实情况下很难达到假设的完美条件，通常由于股票指数组合的复制、跟踪误差、指数构造的变化、股息计算、融资融券成本和交易成本等因素的存在，通过持有成本定价模型计算出来的理论价格和实际价格存在一定偏差，而较大的价格偏差会导致市场的无效性。

在随后的研究中，股指期货定价理论主要沿两个方向发展，第一个方向是探索并定义新的理论模型。包括持有成本定价模型，到目前主要建立了五种期货定价模型。针对利率不变的条件限制，Ramaswamy等首先在连续时间模型中引入随机利率，接着，Hemler等在Cox等人的资产定价一般均衡模型理论基础上，将随机利率和股票现货市场的波动纳入考虑，对市场中常见的股指期货溢价现象做出了一定的解释[2-4]。Klemkosky等考虑交易成本、借贷利率不等及季节性股利等因素提出区间定价模型，利用“做多指数现货，做空指数期货”得到套利区间的上限，“做多指数期货，做空指数现货”得到套利区间的下限[5]。刘志新等人在最优增长投资组合法的基础上解决了连续时间不完全市场条件下期货合约定价问题，提出了不完全市场期货定价模型[6]。

另一研究方向是基于以上五种定价模型，将更多现实因素考虑进来对期货定价模型进一步改进，这也是国内很多学者在期货定价问题上的研究方向。徐国祥和檀向球利用加入市场限制的持有成本定价模型计算理论价格的一个区间，改进的模型更有利于发现套利机会[7]。郑尊信构建了包含现金结算的离散时间下修正持有成本模型，发现改进的模型能够充分考虑结算时间窗口内的风险[8]。张存宬针对借贷利率不同对持有成本定价模型进行改进，得到三个逐步精细的期货价格浮动区间，更加贴切现实[9]。周洲密基于成本定价理论提出无套利区间模型，可用于判断价差是否处于异常状态并基于判断决定是否建立套利头寸[10]。徐国祥和刘新姬改进无套利区间定价模型，使其适用于沪深300股指期货。该模型不仅克服了假设条件太强的缺陷，还提高了定价效率[11]。

以上文献大多是将不完美市场条件加入到模型中对定价模型进一步改进，但在现实情况下不可能将所有不完美条件全部加入到模型中，不完美市场带来的影响往往表现在价格偏差上。目前还没有学者从期货定价偏差分布的角度来对期货定价做进一步研究，所以本文的创新点主要有两点：第一点是将连续混合正态分布模型应用到期货定价偏差分布的研究中；第二点是提出先采用基于牛顿迭代的极大似然估计法对连续混合正态分布未知参数进行有效估计，再进一步利用模拟退火算法对估计结果进行优化。本文深入探讨期货理论价格与实际价格之间的关系，以提高股指期货市场定价的效率，促进期货市场价格发现功能的发挥。同时，本文所使用的研究方法可以用于研究资产收益率和保险损失等问题。

二、模型介绍

(一)期货定价模型

在以往期货定价偏差研究中，大多数学者基于经典的持有成本定价模型计算期货的理论价格[12]。持有成本定价模型是在完美市场假设前提下，根据无套利理论推导出来的。该模型的假设条件有：借贷利率相同且维持不变；无逐日盯市的保证金结算风险；无税收和交易成本；卖空股指成分股无限制；股利发放时间和数量确定，不存在股利不确定风险；股指成分股可无限交割；期货和现货头寸均持有到期货合约到期日。其模型形式如下：

Ft=Ste(r-d)(T-t)

(1)

其中，St表示时间为t时现货指数的价值，r表示t到T时期内连续复利的无风险利率，d表示t到T时期内连续红利率，T-t表示期货合约到期时间，r、d、T-t都是以年为单位，Ste(r-d)(T-t)也就是期货理论价格。

(二)连续混合正态分布模型

1.模型设定

以往研究金融数据时，考虑到正态分布的普遍性和易处理的特性，人们经常假设数据服从正态分布。随着研究的深入，越来越多的学者发现很多金融数据并不服从传统的正态分布假设。曾五一等在研究金融资产收益率时发现它们明显偏离正态分布的假定，呈现尖峰厚尾偏态的分布特征[13]。混合正态分布模型是一种非常灵活和高效的统计建模工具，能满足金融数据的分布特征，主要具有以下几个优点：第一，混合正态分布可以拟合具有厚尾特征的数据；第二，混合正态分布可以拟合单峰或双峰的有偏度数据；第三，混合正态分布和正态分布一样可以具有任意阶的高阶矩[14]。以往研究的混合正态分布主要是两个正态分布混合的离散混合正态分布，但是本文研究的期货价格易受政策或某一事件的影响，在一段时间内发生较大变化，导致偏差可能出现多个峰度。本文研究的Gamma分布与正态分布相结合的连续混合正态分布不仅具有离散混合正态分布的所有优点，还可以拟合具有多峰特征的数据，所以本文引入Gamma分布与正态分布相结合的连续混合正态分布模型来提高拟合偏差的精度。

本文考虑的连续混合正态分布模型X～N(μ，Y)，其中Y～Gamma(α，β)，根据连续情形下的全概率公式得到的密度函数如下：

f(x)=

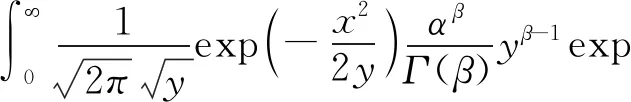
(2)

其中，α为Gamma分布的scale参数，β为shape参数。

2.参数估计

模型形式设定后需对参数进行估计，目前估计混合正态分布模型参数的方法主要有矩估计法、贝叶斯估计法和极大似然估计法。矩估计结果不够精确，贝叶斯估计法常常面临如何选择先验的困难，而单纯的极大似然估计具有收敛速度慢，容易受初始值影响陷入局部最优等缺点[15]。另外，这些方法主要针对离散混合正态分布，而离散混合正态分布的待估计参数多、求解较复杂，所以这些方法并不一定适用于本文Gamma分布与正态分布混合的连续情形。牛顿迭代法能够有效解决极大似然估计法存在的问题，并且极大似然估计量具有无偏估计量中方差最小等优点，故本文先使用基于牛顿迭代的极大似然估计法对该模型进行参数估计，考虑到牛顿迭代求出的是近似解，本文再进一步利用模拟退火算法对牛顿迭代的结果进行优化，最终达到精确估计的效果。

第一步：根据密度函数写出如下似然函数：

(3)

第二步：写出相应的对数似然函数，即对式(3)取对数：

(4)

忽略常数项，式(4)可以简化为：

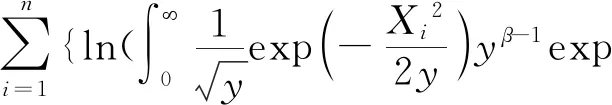
(5)

第三步：求式(5)最大值，可采用导数等于零求未知量的值。先对式(5)关于β求导：

(6)

再对式(5)关于α求导：

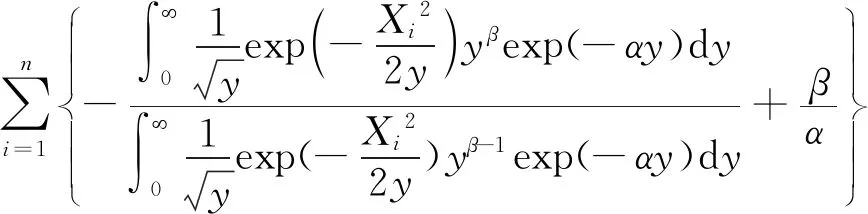
(7)

第四步：求解似然方程。通过式(6)及式(7)很难得到关于α，β的显示表达式，可以通过数值求解的方法得到α，β的近似值。本文将采用牛顿迭代法进行数值计算，牛顿迭代法具有平方收敛的速度，所以在迭代过程中只要迭代较少的次数就可以得到比较精确的解。

牛顿法的迭代格式为：

x(k+1)=x(k)-[J(x(k))]-1f(x(k))，

k=0，1，2，…

(8)

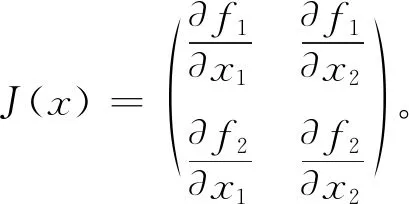
第五步：求解初始值。牛顿迭代的初值从某种程度上影响收敛的结果，所以牛顿迭代的初值不能随意指定，而矩估计量是参数的相合估计量，下面将通过式(2)的矩估计量作为牛顿迭代的初值。

对于式(2)而言，任何奇数阶矩都等于零，所以只考虑偶数阶矩，涉及到两个参数，需要建立两个方程，在这里考虑二阶矩和四阶矩：

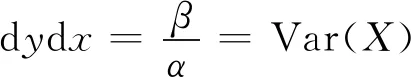
(9)

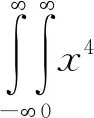
(10)

其中，Var(X)以及Quad(X)分别是样本X的方差和四阶矩。

对式(9)和式(10)求解得到α，β的初始值如下：

(11)

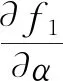
第七步：利用模拟退火算法优化牛顿迭代的结果。模拟退火的基本思想是模拟自然界退火现象，利用物理中固体物质的退火过程与一般优化问题的相似性，从某一初始温度开始，伴随温度的不断下降，结合概率突跳性在解空间中随机寻找全局最优解[16]。

记式(5)为E(α，β)，并作为相应的目标函数，目标是寻找(αi，βj)使得E(α，β)最大，本文具体步骤如下：

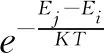
(2) 步骤(1)会得到一个精确解β1，使得在β=β1时，E(α0，β) 最大。这时固定β=β1，将α0扩展到[α-3σ，α+3σ]，再进行退火模拟优化。

(3)重复步骤(1)、(2)，直至|αn-αn-1|+|βn-βn-1|<10-3，停止迭代，找到最优解。

三、数值模拟

为了验证上文提出的估计量求解方法的有效性，现使用蒙特卡洛模拟对连续混合正态分布进行仿真，模拟的具体模型及参数如下：

X～N(0，Y)，其中Y～Gamma(3，0.5)

(12)

利用蒙特卡洛模拟生成服从上述模型分布特征的随机数，并分别求解矩估计量和基于牛顿迭代的极大似然估计量。

通过矩估计，也就是式(11)求解的参数估计结果为(3.626 1，0.609 6)；将上述估计值作为初始值进行牛顿迭代，求解极大似然估计量。

在本次模拟试验中总共经过4次迭代可收敛，各步迭代结果如表1所示。

表1 模拟数据牛顿迭代结果

再将牛顿迭代的结果进行模拟退火优化，最终得到结果(3.100 0，0.506 7)。相比矩估计量(3.626 1，0.609 6)和基于牛顿迭代的极大似然估计量(3.285 9，0.551 7)，可以发现，经过模拟退火优化过的结果和最初设定的模型参数最接近。另外，分别对三个估计量进行Kolmogorov-Smirnov拟合优度检验(后面简记为KS拟合优度检验)。矩估计KS拟合优度检验结果小于0.05；基于牛顿迭代的极大似然估计量KS拟合优度检验结果为D=0.020 333，P=0.564 6；经过模拟退火优化的估计量KS拟合优度检验结果为D=0.015 33，P=0.872 3，说明基于牛顿迭代的极大似然估计量和模拟退火优化的估计量与设定的模拟模型具有一致性。另外无论是直观观察两个估计方法的估计量还是对比KS拟合优度检验结果，都能说明经过模拟退火算法优化的估计量精度得到进一步提高，这也就进一步说明该方法能够更好地应用于拟合期货定价偏差分布。

四、实证分析

(一)数据来源与预处理

本文选取了沪深300股指期货IF1806从2017年10月23日至2018年6月15日期间的相关数据进行实证研究。股指期货以及沪深300指数的收盘价来源于同花顺数据库，无风险利率用上海银行间拆放利率Shibor替代，数据来自上海银行间拆放利率官网，股利收益率相关数据来源于同花顺数据库。由于无风险利率和股利收益率没有统一规范也没有直接指标，下面对这两个指标进行详细说明。

由于中国利率没有完全市场化，国内学者在无风险利率的选取上不尽相同，有学者选取央行票据利率，也有学者选取上海银行间拆放利率。张宝等认为，虽然央行票据利率基本不存在信用风险，但同时也剔除了大部分的市场风险，央行票据利率不适合作为无风险利率，最终选取上海银行间拆放利率Shibor作为无风险利率[17]。本文选取期限与合约剩余期限尽量匹配的Shibor作为无风险利率。

由于Shibor是以年利率(一年 360天)百分比的形式报价，并且表示的是单利利率，而计算股指期货理论价格需要使用连续复利率，因此需要在计算理论价格之前需要对Shibor进一步处理。首先，将Shibor转换成以365天计算的实际利率形式，计算方法如下：

(13)

接着还要将单利的形式转化为连续复利形式，换转公式如下所示：

Rc=mlog(1+R/m)

(14)

其中，m表示一年复利次数，R表示单利，Rc为复利。Shibor的期限分别为隔夜、一周、两周、一个月、三个月、六个月、九个月和一年，所以m值分别取365、52、26、12、4、2、4/3和1。

中国股票市场股利发放包括现金股利和股票股利，但是由于股票股利不会产生额外的现金流，所以本文只考虑现金股利。另外，中国股票市场的股利发放并不是连续的，绝大多数公司在5月和7月之间发放现金股利，如果使用连续股利收益率计算期货理论价格就会出现较大误差，因此不能忽视股利收益率的集中性和周期性。基于以上考虑，在不同月份设定不同的股利收益率，具体计算方式如下：沪深300指数中的成分股一般情况下每半年做出调整，列出每个月沪深300指数的成分股名单，找到每个月每只成分股的股利收益率；中证指数公司在计算沪深300指数时，采用分级投档的方法对每只成分股都赋予了一定权重，用成分股的权重和股利收益率相乘，得到沪深300指数的股利收益率[18]。最终，根据期货定价偏差公式计算得到偏差序列。

表2给出了上述相关数据的描述性特征，对比无风险利率和股利收益率可以发现，无风险利率的变化幅度很小，数据变化相对稳定，而股利收益率波动幅度相对较大，在股利发放淡季，股利收益率几乎为0，股利集中发放时，股利收益率大小超过无风险利率。另外，股指期货收盘价的均值小于沪深300指数收盘价均值，结合只有少数月份股利收益率大于无风险利率的情况，可以推断在大多数情况下，实际价格会小于理论价格，这也与期货定价偏差均值为负的情况相一致。从偏度和峰度来看偏差，偏度为负，说明偏差分布较正态分布为左偏；峰度为正，说明偏差分布具有厚尾性，这与很多金融数据的分布特征相同。

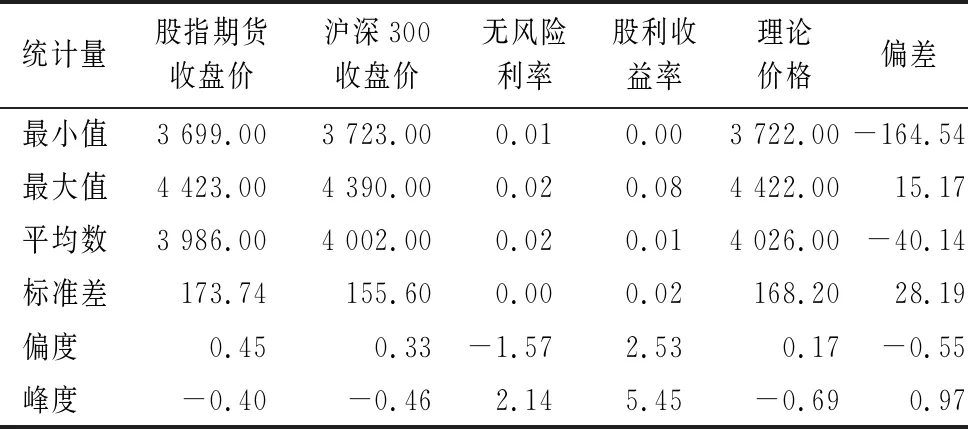
表2 描述性统计量

(二)参数估计与拟合结果

先对偏差序列进行去均值处理，将模型简化为均值为0的混合正态分布模型，图1是去均值后偏差的核密度估计图。

图1中正态分布的均值为0，标准差为实际数据的标准差。对比偏差分布和正态分布可以明显看出，偏差不服从正态分布，并且两者KS拟合优度检验结果远远小于0.05。下面先利用基于牛顿迭代的极大似然估计法对连续混合正态分布模型中未知的两个参数进行估计，将矩估计的结果(0.003 9，3.080 3)作为初始值进行迭代，IF1806实际数据经过了12次迭代收敛，最终得到迭代结果(0.023 7，18.663 8)。

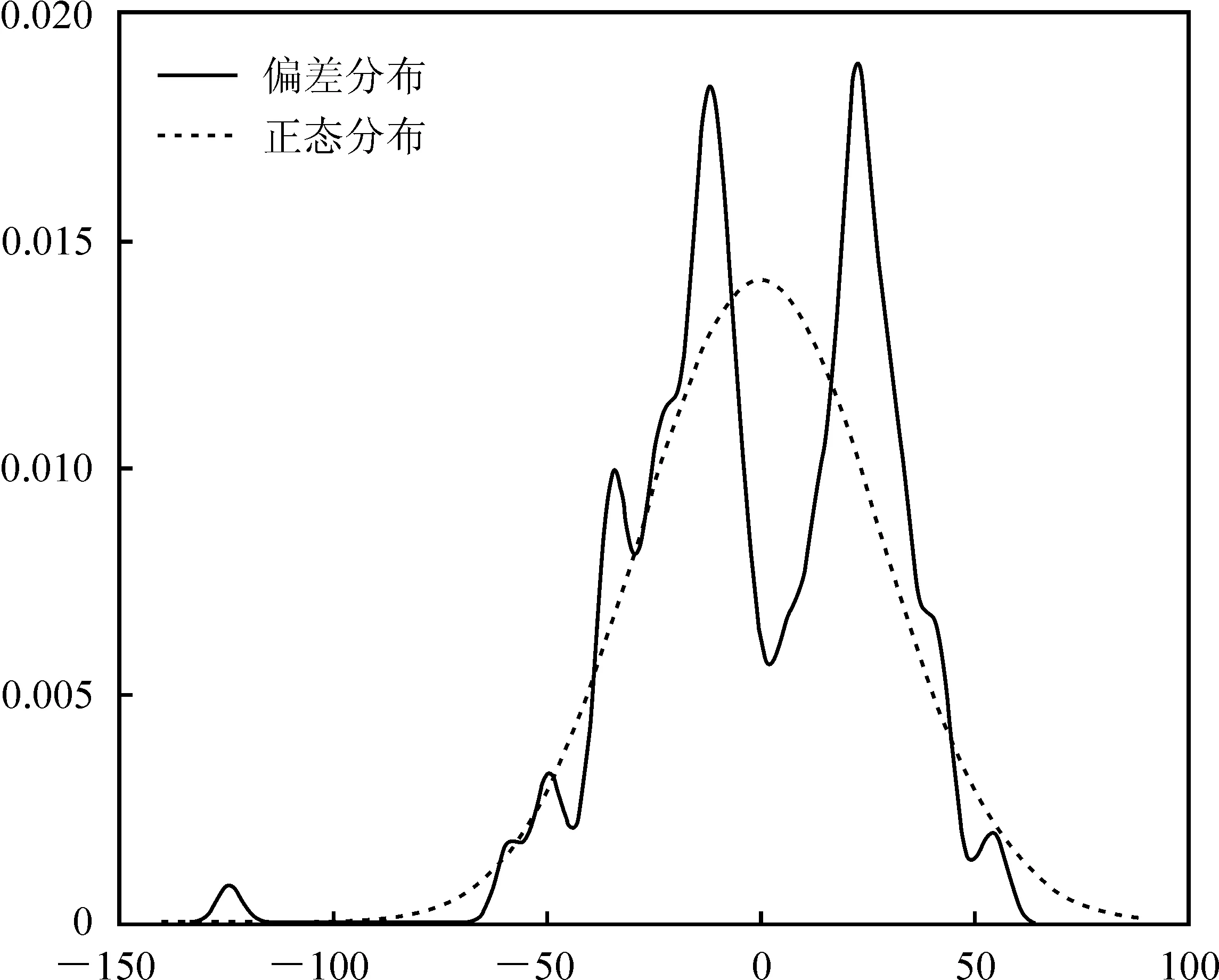
图1 股指期货IF1806的偏差核密度估计图

进一步采用模拟退火算法优化牛顿迭代估计量，得到最终优化结果(0.018 9，18.126 3)。为了进一步体现本文提出的连续混合正态分布模型以及模拟退火算法的有效性，下面从核密度估计图和KS拟合优度检验两个角度对比离散混合正态分布、牛顿迭代混合正态分布和模拟退火混合正态分布。

从图2的核密度估计可以看出，离散混合正态分布、牛顿迭代的连续混合正态分布和模拟退火优化的连续混合正态分布都拟合出了原始偏差数据分布的双峰甚至多峰特征，但无法直接判断哪个模型或方法更优。各模型或方法的两样本KS拟合优度检验结果更具说服力。从表3结果可以看出，直接基于牛顿迭代的极大似然估计得到的模型效果不及离散混合正态分布模型效果，但是经过模拟退火算法优化之后，连续混合正态分布模型的拟合精度得到进一步提高，优于离散混合正态分布模型。

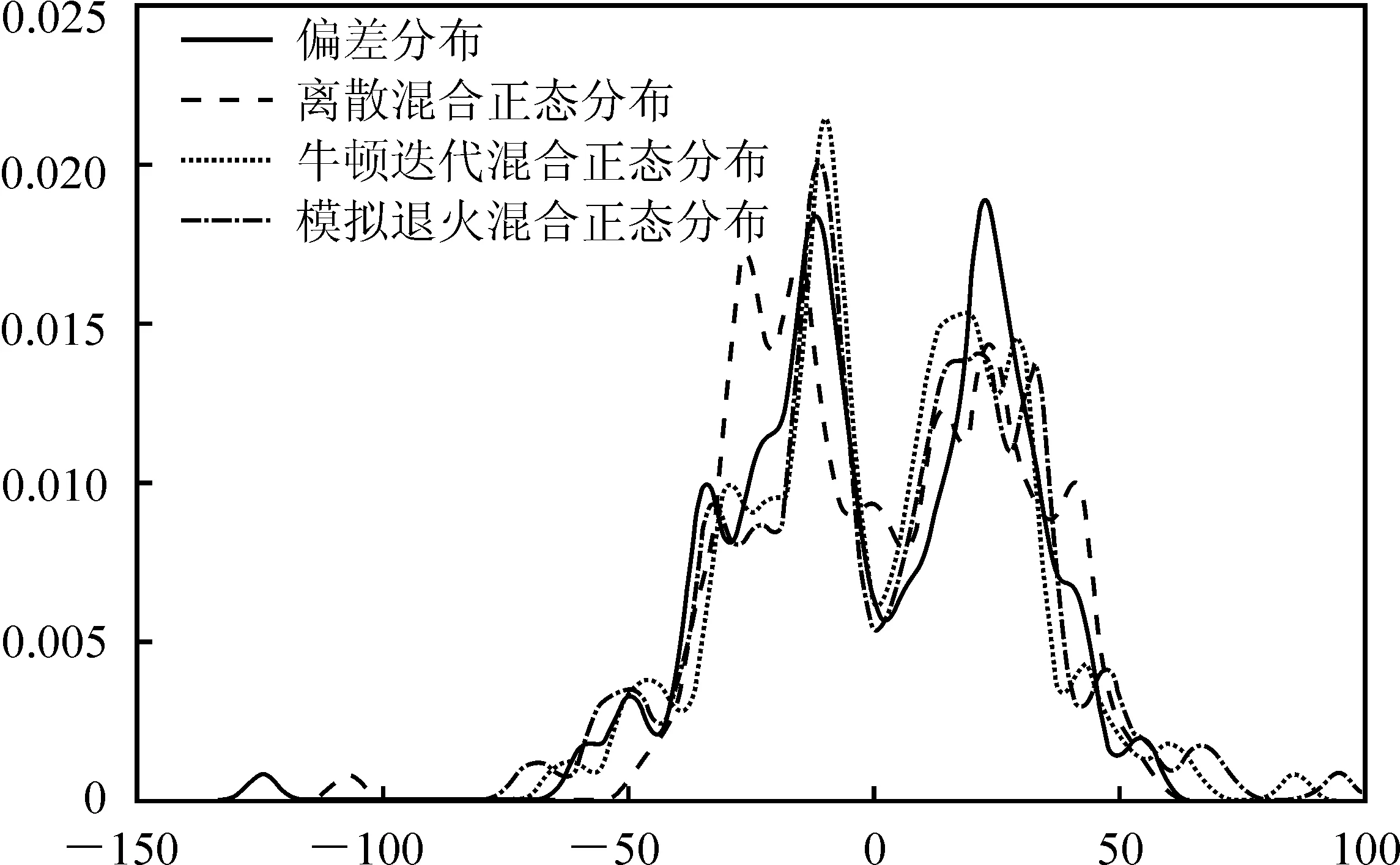
图2 期货合约IF1806的偏差分布拟合图

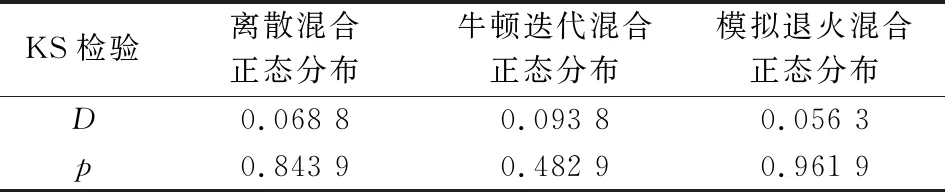
表3 各分布KS检验结果对比

模型X～N(0，Y)，其中Y～Gamma(0.018 9，18.126 3)拟合的是去均值后的偏差，加上均值μ，X～N(0，Y)+μ，其中Y～Gamma(0.018 9，18.126 3)就可以用来拟合实际期货定价偏差分布。

最终发现，期货实际价格与理论价格之间的偏差Xt服从连续混合正态分布。在持有成本定价模型的基础上引入偏差分布可以提高期货定价的准确性，使得模型更加贴近现实，计算的价格更加精确。对于整个股指期货市场而言，期货定价精度的提高有助于改善整个市场的定价效率、充分发挥价格发现功能。图3中，灰色阴影部分是根据前面最终估计出来的连续混合正态分布计算得到的95%置信区间，可以很明显地看出期货价格基本都落在置信区间内。对套利者而言，套利者可以更准确地掌握股指期货实际价格与理论价格之间的关系，当期货价格超出置信区间时存在套利机会，套利者可以据此做出更准确的正向套利和反向套利策略。

图3 套利策略辅助图

五、结论与展望

基于以上研究可以发现，股指期货理论价格和实际价格之间的偏差包含了期货市场种种现实情况，研究偏差分布是提高期货定价准确性的有效方法。首先，基于Gamma分布和正态分布相结合的连续混合正态分布不仅可以拟合具有厚尾特征的数据，而且可以拟合具有偏度和多峰特征的数据，本文提出使用该连续混合正态分布对偏差分布进行拟合。接着，本文给出了该连续混合正态分布的参数估计方法，先通过矩估计给定牛顿迭代的初始值，接着利用基于牛顿迭代的极大似然估计法对模型参数进行估计，之后再利用模拟退火算法对估计结果进一步优化。为了验证该估计方法的有效性，本文进行了蒙特卡洛数值模拟实验，实验表明该方法表现稳健，能够有效估计模型参数。最后，通过股指期货IF1806的实际数据进行偏差分布拟合和比较，发现混合正态分布能够准确拟合股指期货实际价格和理论价格之间的偏差分布，并且偏差分布的精确估计可以提高股指期货定价准确性，对整个市场和套利者都具有现实意义。

越来越多的实证表明金融数据并不服从传统的正态分布假设，一方面，本文所提出的连续混合正态分布可以应用在许多其他金融研究中，例如可以应用于金融资产收益率的问题。对收益率的准确拟合是证券市场风险管理和价格趋势预测的基础。早期的金融研究者都假设资产收益率近似服从正态分布，但是大量实证表明资产收益率的分布呈现尖峰特征，而且偏度为负，一般分布很难进行拟合。本文使用的混合正态分布不仅可以拟合这样的分布，而且只需要估计两个未知参数，和现有文献中由两个正态分布的混合相比，需要估计的参数个数较少。另外，混合正态分布还可以用于保险损失数据的拟合，保险损失数据往往也是左偏的，从数据分布特征来看本文的混合正态分布模型对其也具有适用性。另一方面，还可以考虑将其他分布与正态分布相结合，本文只是将Gamma分布与正态分布相结合，将正态分布与其他分布相结合是本文接下来研究的一个方向，希望能发现其他混合正态分布更多的优点，拓宽混合正态分布的应用面。