基于神经网络观测器的水下拖体输出反馈姿态控制

井安言， 佘湖清

(宜昌测试技术研究所, 湖北 宜昌 443003)

0 引言

21世纪是海洋的世纪，人类对于海洋的探索永不停歇，水下拖体作为一种高效且安全的平台广泛用于多种场合，如：水下勘探、海洋监测和水声对抗等，平台上可搭载多种声呐探测设备、温盐深(CTD)传感器和化学元素探测传感器[1]，以完成各类科考或军事任务。水下拖体属于一类水下航行器，其外壳上一点与拖缆一端相连，拖缆另一端与拖曳母船连接。拖体的姿态控制一直是科研人员十分重视的课题，而其中俯仰控制又是姿态控制中非常重要的一环。由于拖体平台的工作环境恶劣，工作要求苛刻，对于拖体的可控性需求也极其迫切。

国内外学者相继开展了关于水下拖曳系统水动力理论和稳定性分析的研究[2-9]。Blintsov等[10]针对拖体在小深度拖曳情况下的特点，提出在不确定条件下使用局部功能最小化的方法进行运动控制，改进条件积分方法以消除工作中的积分饱和，基于2阶控制律合成俯仰和横滚控制器，并综合单元旋转运动控制系统以达到解耦的作用。Nakamura等[11]和Kajiware等[12]研究了具有自推进模式和拖曳模式的水下航行器 “DELTA”，在两种模式下均设计了基于线性二次型积分(LQI)的控制器和基于线性矩阵不等式(LMI)的H∞鲁棒控制器。之后考虑受到波浪振荡和速度变化干扰的拖体，基于线性变参数(LPV)控制理论提出一种鲁棒控制策略，该控制策略相较于PI控制和LQI控制有更好的效果。Campa等[13]认为可以使用H∞鲁棒理论克服复杂非线性模型固有的不确定性，非线性和线性模型之间的差异以及其他未知干扰，提出了一种在设计过程中自动选择加权函数的方法以及一种多变量识别过程的自适应方案，以在更广的修整范围内提高性能，Teixeira等[14]设计并证明了一种基于Lyaounov的非线性自适应控制器，以解决拖体的俯仰和深度控制问题。

考虑到一些水下航行器为了减轻质量、降低成本以及避免过多传感器带来的测量误差和测量噪声等目的，本身不会搭载足够的传感器，导致系统状态变量无法全部反馈。针对这一问题，许多文献提出设计观测器的方法[15-21]，张利军等[15-16]在文献[15]中根据可测量的深度和纵摇角设计观测器实现不可测纵摇角速度反馈，在文献[16]中考虑近水面自主水下机器人(AUV)受波浪干扰，设计观测器估计AUV姿态、速度和波浪位移、速度，并将系统输出信号中的波浪干扰分离。Liu等[17-18]提出了一种用于AUV的非线性无源观测器，无需声学多普勒测速仪便可实现滤波操作以及对无法测量的波浪速度和AUV相对波浪速度的重建。杨盼盼等[19]设计了一种分布式观测器，对AUV集群中邻居速度信息进行实时估计。Minowa等[20-21]对一种拖体系统设计了高增益观测器与线性卡尔曼观测器进行状态估计，并将估计值输入基于LQI设计的鲁棒控制器，用来控制拖体的深度和俯仰姿态。此外，水下航行器一般使用惯性测量单元(IMU)测量角速度，IMU需要安装在航行器重心位置才可以比较准确地测量角速度。

本文研究对象拖体在执行不同种类任务时会搭载不同设备，有时甚至会外挂设备，拖体重心难免会发生变化，这种情况下IMU的测量精度无法保证，所以本文设计了一种基于神经网络观测器的拖体姿态补偿控制系统，该系统由两部分组成：一是状态观测器，二是补偿滑模控制器，两部分中各包含一个径向基函数(RBF)神经网络和独立的权值更新自适应律，其中控制器部分含有一种映射修正自适应律，以保证控制律不会产生奇异，两个RBF神经网络在线辨识模型中的未知非线性函数。基于Lyapunov理论证明了系统的稳定性，仿真和实验结果表明，所设计的补偿控制系统可以保证当拖体存在有界干扰以及未建模动态情况时仍然具有良好的控制性能。

1 模型描述

通过对AUV六自由度动力学模型[22]修改并解耦后可得拖体垂直面俯仰通道动力学模型为

(1)

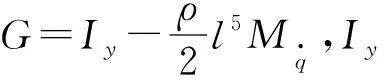
由(1)式可知拖体动力学模型具有较强的非线性和不确定性，考虑模型误差和其他干扰，可表示为如下单输入单输出非线性系统：

(2)

2 基于观测器的姿态补偿控制系统

2.1 传统状态观测器设计

对于系统(2)式，可以设计传统状态观测器[23]如下：

(3)

(4)

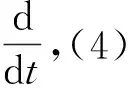
(5)

引理1如果AH是Hurwitz矩阵，Q是正定矩阵，而且严格正常有理函数H(s)=cT(sI-AH)-1b是严格正实的，I为单位矩阵，则一定存在正定矩阵P，满足

(6)

引理2存在线性时不变状态方程

(7)

式中：x(t)∈R，u(t)∈R，AH∈R，BH∈R. 初始值为x(0)=x0. 对(7)式中的任意解存在不等式

(8)

式中：k1随x0以指数形式衰减为0的正常数；k2为与AH的特征值有关的正常数；α为正常数。

2.2 自适应神经网络状态观测器设计

2.2.1 RBF神经网络

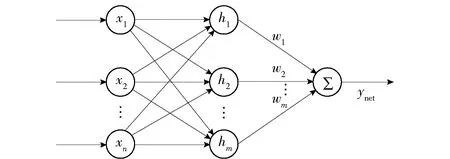
图1 RBF神经网络结构Fig.1 RBF neural network structure

考虑到观测器(3)式中需要估计未知非线性函数f(x)和g(x)，可以采用RBF神经网络[25-26]对其进行逼近估计，其结构如图1所示。图1中:x1、x2、…、xn为神经网络输入；w1、w2、…、wm为输出层权值；m为输出节点的数量；h1、h2、…、hm为隐含层输出的非线性激活函数，ynet为网络输出。

(9)

式中：cj(t)为第j个隐含层神经元的中心点向量值；bj为隐含层神经元j的高斯基函数宽度，其值为正。网络输出为

(10)

式中：wi为输出层权值。

2.2.2 观测器误差动态和结构

根据RBF神经网络的函数逼近特性，系统(2)式中的未知非线性函数可以由理想权值W和基函数h表示为

(11)

(12)

因此，传统观测器(3)式和观测误差动态方程(4)式可写为

(13)

和

(14)

为表述方便，后文中函数的部分自变量均省略。

(12)式代入(5)式，可得系统输出估计误差为

(15)

2.2.3 观测器稳定性分析

对(15)式进行滤波处理：

(16)

(16)式的状态空间实现为

(17)

假设控制输入信号u(t)有界，即|u(t)|≤ud，针对观测器方程(13)式，设计鲁棒项为

(18)

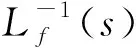
定理1设计RBF神经网络权值自适应律为

(19)

证明定义Lyapunov函数为

(20)

(21)

(22)

(23)

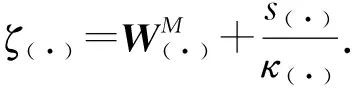
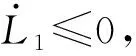
条件1

(24)

条件2

(25)

证毕。

(26)

根据1阶线性齐次微分方程求解公式，对(14)式求解，得

(27)

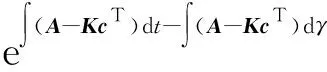
根据引理2和(26)式，可得

(28)

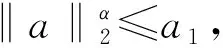
(29)

式中：a1、a2和a3为正常数。

2.3 自适应神经网络补偿滑模控制器

2.3.1 控制器结构和误差动态方程

对于系统(2)式，考虑到系统状态变量x由2.2节神经网络状态观测器估计得到，记为，干扰d(t)视为未知非线性函数的一部分，即令f′()=f()+d(t)，则(2)式可写为

(30)

(31)

设计神经网络权值自适应律为

(32)

设计滑模函数为

(33)

式中：c>0且满足Hurwitz条件；设计滑模控制律为

(34)

式中：ψ>0.

(35)

式中：δ1和δ2为正常数；Pc是一个正定矩阵，且满足

ΔTPc+PcΔ=-Qc，

(36)

Qc为任意正定2×2阶矩阵。

基于观测器的拖体俯仰姿态补偿控制系统结构如图2所示。

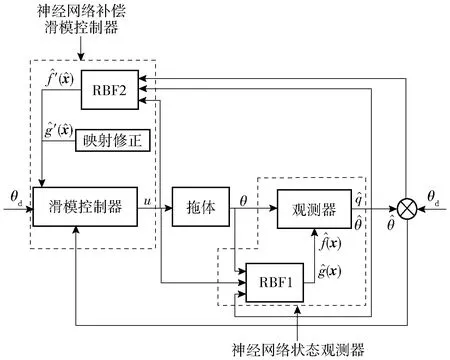
图2 基于观测器的拖体俯仰姿态补偿控制系统结构图Fig.2 Block diagram of observer-based attitude compensation control system for towed underwater vehicle

2.3.2 控制系统稳定性分析

控制律(34)式代入系统(30)式，得系统闭环动态方程的向量形式为

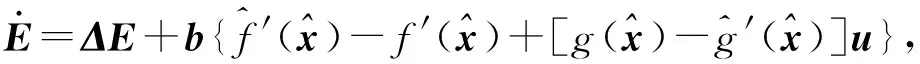
(37)

ω1=′(|W1)-f′())，

(38)

根据(31)式，(36)式可改写为

(39)

定义Lyapunov函数为

L=L1+L2+L3，

(40)

式中：L2和L3分别为

(41)

(42)

(43)

神经网络权值自适应律(32)式和映射修正自适应律(35)式代入(43)式，得

(44)

对L3求导并将滑模函数(33)式和动态方程(36)式代入，得

(45)

滑模控制律(34)式代入(45)式，则

(46)

对映射修正自适应律进行分析，可得如下结论：

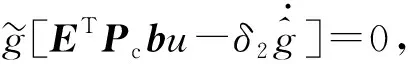
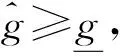
3 仿真算例与实验结果

3.1 仿真算例

首先，在标称情况下，设俯仰角指令为θd=0.1sin(t)，对补偿控制系统和PD控制系统进行仿真计算，比较两种控制系统的响应情况以及角速度的观测精度。然后，在相同指令下，考虑存在水动力和力矩偏差、舵机死区、外界干扰以及拖缆张力变化的情况，比较两种控制系统的鲁棒性。

3.1.1 有效性检验

标称情况下， 图3(a)为两种控制系统的正弦响应曲线，图3(b)～图3(d)为角速度的观测结果和精度，图3(e)为艉水平舵角响应曲线。由图3可知：补偿控制系统的响应曲线光滑，经过短时间的学习可以快速跟踪俯仰角指令曲线；PD控制系统的响应曲线比较粗糙，尤其在曲线峰值处会出现小振荡，跟踪误差较大；神经网络观测器能够在角速度初始状态存在偏差的情况下，仅用时1 s快速收敛到真实值，并随后完成无差估计；传统状态观测器始终存在较大的估计误差。以上结果表明，在满足一定条件下，本文所设计的3种自适应更新律和两个RBF神经网络可以对模型中的非线性、不确定部分进行在线辨识和实时补偿，有效提高控制效果和观测精度。

图3 标称情况下仿真结果Fig.3 Simulated results under normal conditions

3.1.2 鲁棒性检验

图4 拖曳力垂向分量Fig.4 Vertical component of drag force

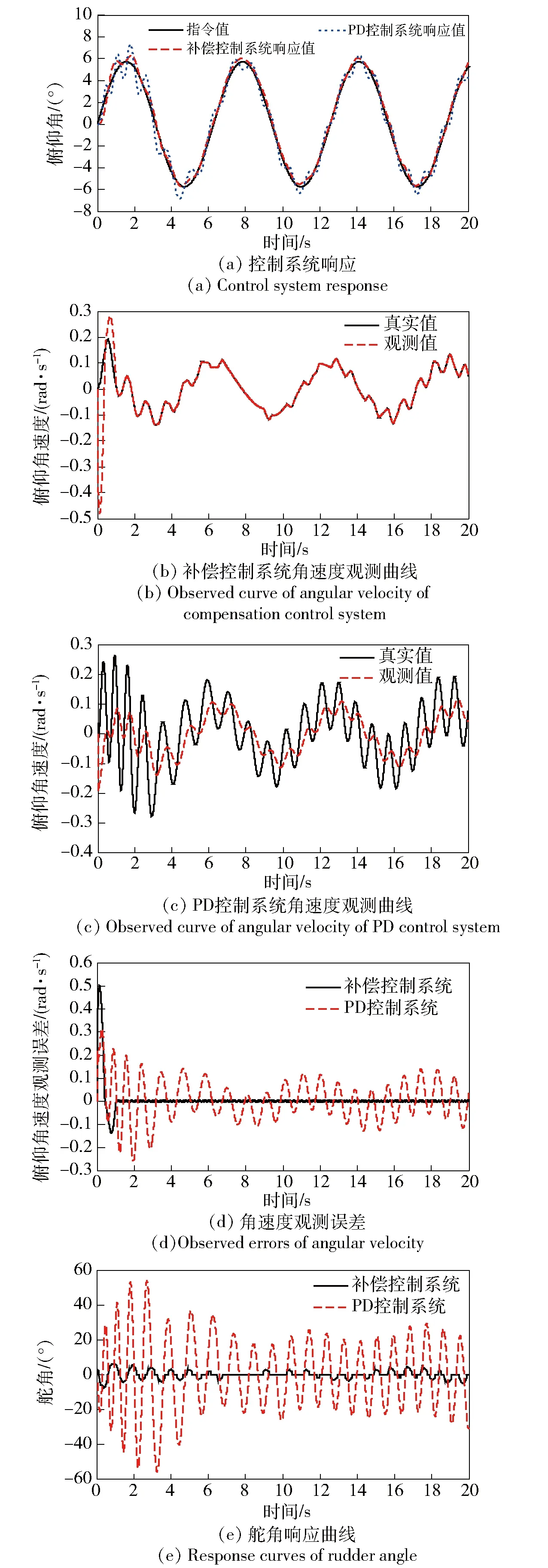
图5 扰动情况下仿真结果Fig.5 Simulated results under disturbance conditions

3.2 实验结果

以某型号拖体为实验平台，在海况约3级、拖体定深7～9 m、航速4～6 kn的工况下，得到控制算法实验结果如图6所示。由图6可见，PD控制系统作用下的俯仰角变化范围为-3°～8°，补偿控制系统在经历约20 s的学习过程后控制俯仰角稳定在0°～3°. 相比之下，补偿控制系统的控制效果更出色。

4 结论

本文针对拖体俯仰姿态控制系统设计中模型强烈的非线性不确定性以及外部干扰的问题，提出了自适应神经网络和映射修正自适应律逼近模型未知非线性部分和常数项的方法，实现了无需拖体精确模型的状态观测和补偿控制。设计了两种神经网络权值更新自适应律，实现两种神经网络在线辨识拖体非线性动力学模型并加入鲁棒项抑制附加干扰，以及一种映射修正自适应律，保证控制律不产生奇异。基于Lyapunov理论证明在满足一定条件时系统的误差是最终一致有界的。仿真和实验结果表明，本文设计的补偿控制系统具有优异的鲁棒性和自适应性，可以在模型系统存在水动力和力矩偏差、舵机死区、外部干扰以及拖曳力变化的情况下，实现对系统状态的精确估计和有效控制。