黎曼几何在计算机视觉中的应用研究进展*

史泽林，刘天赐，刘云鹏

(1.中国科学院沈阳自动化研究所·沈阳·110016； 2. 中国科学院机器人与智能制造创新研究院·沈阳·110169； 3. 中国科学院光电信息处理重点实验室·沈阳·110016)

0 引 言

在计算机视觉中，基于黎曼几何的流形方法已成为了一个重要的研究方向。其前提是数据满足流形假设，即呈现在高维空间中的源自现实世界的真实数据往往分布在一个低维流形空间上，流形的维度与其所“嵌入”的高维欧氏空间的维度相比要低很多。这种先验假设似乎特别适合于完成人工智能(Artificial Intelligence, AI)领域的相关任务，如涉及图像、声音或文本识别处理等的工作任务。因此，研究人员很自然地考虑到用流形来表示输入空间的变化分布，从数据的流形观点出发，对数据潜在的流形结构进行建模。这一方法论充分利用了黎曼流形的几何性质，因而又被称作黎曼几何流形方法，即黎曼流形方法。

在图像分析领域中，有学者将特征协方差矩阵作为区域描述子[1]。此时，该描述子即为分布在正定对称矩阵流形上的数据点。例如，对于图像集合而言，用子空间来表示图像集是一种常见的方法[2]。此时，用来表示图像集合的子空间便可被视为分布在Grassmann流形[3]上的数据点。这样，图像集合也可被视为分布在Grassmann流形上的不同的数据点。

本文重点介绍了黎曼流形方法在计算机视觉领域中的研究现状。首先，简要介绍了黎曼流形的一些重要概念，并结合若干典型视觉任务，介绍了几种常用的黎曼流形；随后，就黎曼流形的视觉应用，总结了目前国内外相关的研究现状及具有代表性的工作，着重介绍了近几年来黎曼流形与深度学习相结合的研究进展；最后，对在机器学习领域中引入黎曼流形的未来发展方向进行了讨论。

1 黎曼流形的基本概念

拓扑流形，简称流形，是在局部与欧氏空间同胚的拓扑空间，而微分流形是具有全局可定义微分结构的拓扑流形。对于微分流形而言，流形上每个点都对应着切空间，该点的切空间是由经过该点所有曲线的切向量组成的向量空间。

黎曼流形是一种特殊的微分流形，即一种具有黎曼度量的微分流形。具体而言，黎曼流形在其上的每个点的切空间中均赋予了相应内积，而所有切空间上对应的内积便被称作黎曼度量。黎曼度量是黎曼流形最重要的性质，它使我们能够在流形上定义各种几何概念，例如两条曲线之间的角度和曲线的长度。对于黎曼流形而言，将流形上两点之间的最短距离定义为连接两点间的最短曲线的长度，并将该最短距离称为测地距离；相应地，连接此两点的最短曲线则被称作测地线，该最短曲线类似于欧氏空间中两点间的直线段。由黎曼度量推导出的测地距离是度量黎曼流形上两点之间距离的最本质的几何度量，在图像处理和模式识别领域中有着重要应用。

1.1 黎曼度量

定义1:设M是m维光滑流形，对于流形上的任一点x∈M，存在切空间TxM，其上切向量长度的定义为对M的每个切空间TxM赋予一个内积g(x)=<,>x:TxM×TxM→R。任意的切向量U,V∈TxM，若满足以下性质：

• 对称性：g〈U,V〉x=g〈V,U〉x；

• 正定性：g〈U,U〉x>0，如果X≠0

则称(M,g)为一个m维黎曼流形，g称为黎曼度量。

1.2 黎曼流形上的测地线距离

在黎曼流形(M,g)上，曲线γ:[a,b]→M的长度为

(1)

而黎曼流形(M,g)上的任意两点x,y∈M的黎曼距离为

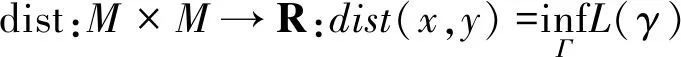
(2)

式(2)中，Γ是M上连接点x和点y的所有曲线的集合。其中，黎曼距离满足以下性质：

•正定性：dist(x,y)≥0。其中，当且仅当x=y时，有dist(x,y)=0；

•对称性：dist(x,y)=dist(y,x)；

•三角不等性：dist(x,z)+dist(z,y)≥dist(x,y)

测地线指的是连接任意两点x,y∈M的所有连续可微曲线γ:[a,b]→M中长度最小的曲线，即

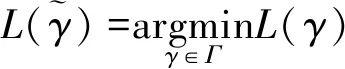
(3)

从图像的几何角度出发，测地线距离为图像集合的内在关系在流形空间上的度量。

1.3 黎曼流形上的映射

给定黎曼流形M上的任意两点X,Y∈M，X和Y之间的最短路径定义为连接这两点的测地线γ(t),t∈[0,1]。切空间TXM是由所有切向量V∈TXM构成的。其中，切向量V的长度等于流形M上点X和点Y之间测地线的长度。黎曼对数映射RlogX:M→TXM通过映射RlogX(Y)=V将点X和点Y之间的测地线(如图1中的虚线所示)从流形M映射到切空间TXM中，而黎曼指数映射RexpX:TXM→M通过映射RexpX(V)=Y，将切向量V映射回原始的流形空间。在黎曼流形中，通过这一方法，流形上测地线的长度等价于根据黎曼对数映射在切空间中获得的对应切向量的长度。即对于流形上的任意两点X,Y∈M，结合测地线和黎曼指数映射可知，黎曼流形上两点间测地距离的计算公式为

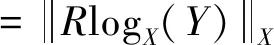
(4)

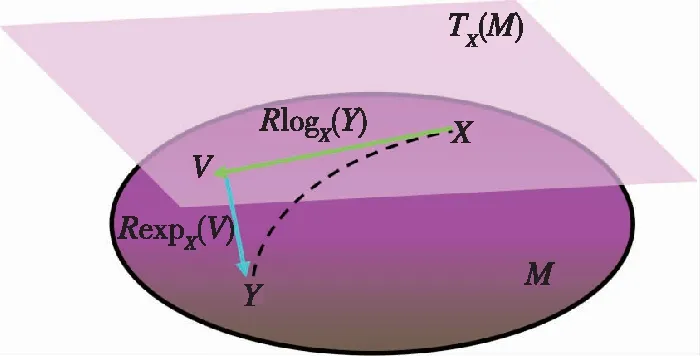
图1 黎曼流形上的指数映射和黎曼对数映射示意图Fig.1 Schematic diagram of exponential mapping and Riemannian logarithmic mapping on Riemannian manifolds

2 黎曼几何与图像的关系

对于计算机视觉而言，许多视觉数据与黎曼流形有着密不可分的联系。例如：在目标跟踪过程中，图像的几何变换构成SL(3)群；图像序列和视频可以依据特征子空间进行建模，从而具有Grassmann流形结构；在图像处理与模式识别领域中，协方差矩阵作为图像的特征表征，具有良好的正定对称结构，进而可以利用正定对称进行流形建模。总体而言，图像与黎曼流形的关系主要体现在两个方面，一方面是图像中目标发生的几何变换在流形空间中的分布；另一方面，是图像特征空间构成了图像在黎曼流形空间中的几何分布。接下来，总结了在计算机视觉领域中被广泛应用的几种李群及黎曼流形，以此来具体介绍黎曼几何与图像的关系。

2.1 图像变换和黎曼流形

在计算机视觉中，在跟踪和检测目标时，目标不可避免地会经历几何变换。考虑到图像的几何结构，可以通过某些具有群结构的运动变换群来描述视觉模式的特征[4-5]。对图像中的几何变换群进行分析，在包括目标跟踪、目标检测和图像配准等[6-9]在内的许多视觉任务中均有着广泛应用。

在计算机视觉中，可以通过齐次坐标系下的线性方程来表示图像的几何变换，相应的几何变换矩阵可以用一个3×3的非奇异矩阵表示，该矩阵被称为单应矩阵。具体而言，给定任意的图像I1，其灰度值可表示为I1(p)，而I1经过几何变换后的图像I2的灰度值可表示为I2(T(p;r))。相应地，两幅图像的灰度值关系可用下列线性方程表示

I2(T(p;r))=I1(p)

(5)

在这种情况下，经过几何变换后的图像像素间的关系可表示为

(6)

式(5)表示的是变换后的图像相对于原始图像的几何变换，且p=(x,y)T是图像像素的位置坐标，r=(r1,r2,…,r8)T表示的是对应的参数向量。

因此，单应矩阵的定义如下

(7)

进而，归一化后的单应矩阵具有了特殊线性群的流形结构，构成了具有以下结构的李群

SL(3,R)={X∈GL(3,R):det(X)=1}

(8)

式(8)中，GL(3,R)是由可逆的3 × 3实矩阵组成的一般线性群。

李群是具有黎曼流形可微分结构的矩阵李群, 可以将其理解为一种特殊的黎曼流形。同一目标在不同角度下获得的图像，其图像间经历的几何变换构成的几何变换矩阵，分布在黎曼流形空间中。针对图像几何变换与黎曼流形的关系的研究,文献[4]通过建立目标在图像中经历的几何变换矩阵的可视化模型，直观验证了图像几何变换在流形空间中的几何分布，揭示了图像与黎曼流形之间的内在联系，其目标的图像几何变换的可视化结果如图2所示：(a)为体育场目标在不同距离下的拍摄图像；(b)为在不同距离下成像的目标图像间的几何变换关系所对应的可视化结果。在图2(b)中，其坐标轴对应三维空间中的虚拟坐标，其点间距离反映了图像几何变换的剧烈程度。

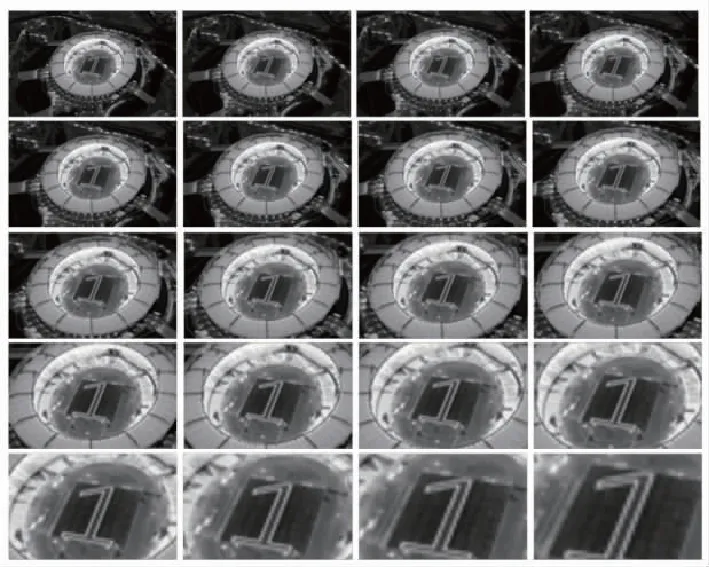
(a)

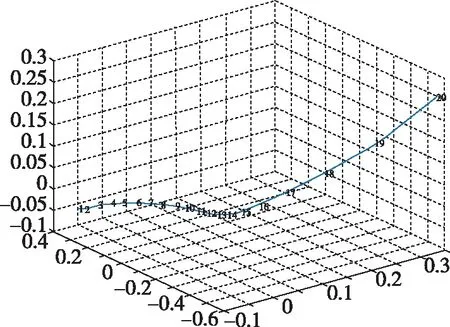
(b)图2 图像几何变换的可视化结果Fig.2 Visualization results of image geometric transformation

2.2 图像特征和黎曼流形

近年来，利用特征协方差矩阵描述目标的目标建模方法受到日益广泛的关注。如图3所示，用目标的灰度、梯度、小波和空域信息等多种特征构建协方差矩阵以描述目标，特征协方差矩阵的集合构成了正定对称流形。正定对称(Symmetry Positive Definite，SPD)流形在计算机视觉领域中有着各种各样的应用[10]。比如，特征协方差矩阵可被应用在目标检测[11]、纹理分类[12-13]、动作识别[14-15]等领域，分散张量成像(Diffusion Tensor Imaging，DTI)是SPD流形的另一个主要应用方向[16]。关于正定对称流形的几何学论述可参见文献[17-18]，其给出了正定对称流形上的黎曼指数映射及其逆映射的解析表达式。特别地，文献[17]给出了正定对称流形上的两种不同的数学结构，即具有仿射不变黎曼度量的普通黎曼结构和具有双不变黎曼度量的新的李群结构。需要特别指出的是，后者并不是普通意义上的矩阵李群，其上的双不变黎曼度量的存在使得流形上的测地距离和黎曼均值的计算变得十分简单。另外，文献[19]研究了正定对称流形上的多变量正态分布，分析了黎曼曲率对正态分布的影响，值得关注。

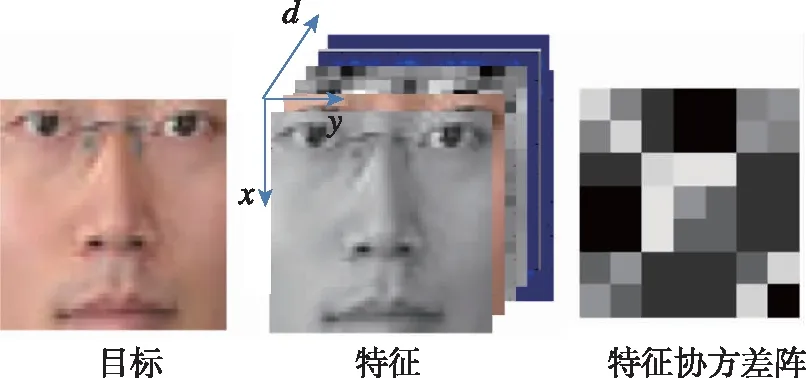
图3 目标的特征协方差矩阵建模Fig.3 Target characteristic covariance matrix modeling

当所涉及数据集的单个数据均位于某个线性空间的子空间时，可用格拉斯曼(Grassmann)流形描述该数据集。Grassmann流形主要可用于对图像集和视频进行建模，图像集合间的内在关系可以表示在流形空间上，图像在黎曼流形上的空间分布如图4所示。利用Grassmann流形对图像进行建模具有不受光照条件、拍摄角度影响等优点，进而可被广泛地应用在人脸识别[20-21]、动作识别[22]和运动群分析[23]等方向。在基于图像集的人脸识别中，同一个人的人脸图像集被表示为线性子空间。由于线性子空间具有严格的Grass-mann流形结构，可以将这些人脸图像集表示为Grassmann流形上的数据点。比如，在宽松的假设下，同一目标(如人脸)在变化的光照条件下，所得到图像的集合分布在一个多维子空间中[24]，全部的子空间集合构成 Grassmann 流形。如图5所示，假设每幅图像的大小是n×n，每组图像集有p幅图像，则图中的四组图像集分别对应 Grassmann 流形G(n2,p)上的四个点。文献[25]综合核函数方法和稀疏编码的优点，拓展核稀疏子空间聚类模型至Grassmann流形，将稀疏子空间聚类方法与核函数方法相结合，学习Grassmann流形的核稀疏表示，提出了一种基于Grassmann流形的图像集聚类方法,用于人脸聚类。在动作识别中，特征子空间则由包含特定动作的图像序列计算获得。文献[26]从黎曼流形的几何角度出发，提出了一种从流形到流形的Grassmann几何降维方法。该模型提出了一种具有正交约束的降维方法，进而将降维问题转化为Grassmann流形上的优化问题，在降维的同时提升了动作识别的识别效果。关于 Grassmann 流形的数学分析及几何属性,详见文献[27]和文献[28] 。文献，给出了关于 Grassmann 流形的不同理解和矩阵描述，以及 Grassmann 流形上的黎曼指数映射和对数映射，还特别分析了 Grassmann 流形上的各种优化算法。许多计算机视觉领域的相关文献(如文献[29]和文献[30])引用了 Grassmann 流形上的各种距离度量，有关这些距离度量的理论分析均源自关于 Grassmann 流形微分几何学的文献[31]。目前，针对Grassmann 流形方法的应用研究方兴未艾，这些研究包括通信信道中的最优预测和编码问题,航天飞机外形设计中的流形插值运算,以及运动分割问题所涉及到的流形聚类问题等。

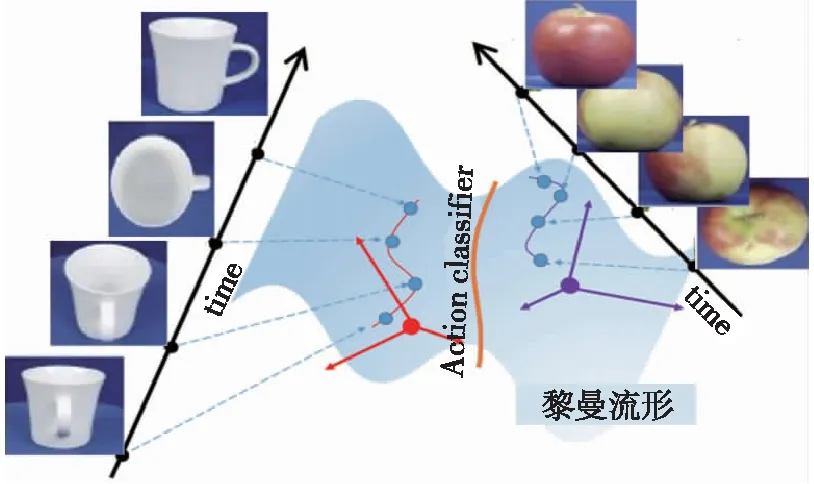
图4 图像在黎曼流形上的空间分布Fig.4 Spatial distribution of images on Riemannian Manifolds

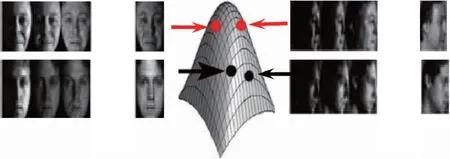
图5 变化光照条件下的图像集构成Grassmann流形Fig.5 Grassmann manifolds constructed by image sets under varying illumination conditions

3 黎曼流形在计算机视觉中的应用

3.1 基于黎曼流形的几何方法

早期的流形方法经历了不同的发展阶段。主成分分析(Principal Component Analysis，PCA)方法[32]可以看作是最初的流形几何方法原型。PCA方法以线性流形为模型，其最初的设计目的是找出最接近数据点云的线性流形。主成分是指输入数据映射在流形上的成分，它对应着流形上的内蕴坐标。对于非线性流形而言，其学习模型主要基于构建邻接图来学习参数映射矩阵。基于邻接图的流形几何方法主要将从训练数据中学习到的参数映射矩阵应用到新的数据中，从而获得新数据的流形映射。流形学习这一概念的提出可以追溯到2000年局部线性嵌入(Locally linear Embedding)方法[33]和等距映射(Isomap)方法[34]在国际著名期刊Science上的发表。局部线性嵌入方法是一种无监督的流形学习方法，它认为数据在局部满足线性关系，即每个数据均可由其邻域中的几个样本线性表示，通过构建加权邻接图来获得高维数据的低维表示，并在学习到的低维表示中保持原始数据间的局部线性关系；等距映射方法是一种全局模型，该方法通过构建数据的全局邻接图，将计算两点间的测地线距离转换为计算两点间在邻接图上的最短路径距离，通过测地线距离替代欧氏距离。拉普拉斯特征映射方法[35]通过构建无向加权图来描述数据的流形结构，然后通过图嵌入方法获得数据的低维表示；半监督嵌入方法[36]通过学习邻接图对流形结构进行直接编码，该方法中的参数化神经网络结构可同时对流形嵌入映射和分类器进行学习。此类流形方法的主要目的是学习数据样本中的潜在流形结构，而其潜在流形结构是未知的。这类方法常常假设数据样本中的噪声较少，不带噪声的样本分布在流形上，而噪声样本的分布远离流形，因此此类方法往往对噪声敏感。

然而，现实数据中的复杂数据具有更为复杂的非线性流形结构。当构建的邻接图难以有效表达数据间的结构时，对于复杂数据的建模要借助局部线性切空间方法[37-42]。与早期基于构建邻接图的流形方法相比，此类方法的最大不同之处在于其所使用的流形种类是已知的，即可以清楚地知道数据中所蕴含的流形的种类。而在计算机视觉和机器学习领域，许多相关算法，包括支持向量机(Support Vector Machine，SVM)、PCA等经典算法,均无法被直接应用于流形数据。如果忽略流形数据的几何结构，直接把这些基于欧氏结构的方法应用在流形数据上，正如文献[43]和文献[44]所提及，通常会产生不理想的效果。当需要处理的流形数据具有黎曼结构时，一种常用的方法是通过将流形数据映射到流形上某一特定点的切空间来处理流形的非线性结构，这一特定点通常选取为数据的均值点。文献[11]是基于切空间映射方法的最成功的算法之一，它提出了一种在黎曼流形上进行学习的行人检测方法。该方法将协方差矩阵作为目标特征描述子，在静态图像中检测行人。然而，将流形数据映射到切空间的方法仅仅是对流形非线性结构的一阶近似。该方法的局限在于，当数据分布远离切空间原点时，该框架下的近似结构易发生扭曲。除此之外，迭代地进行流形空间与切空间之间的映射操作具有极高的计算复杂度。对于基于切空间映射的方法而言，切空间原点(即参考点)的选择至关重要。切空间原点选择的质量严重影响着近似方法的准确性，选择几何特性良好的切空间原点以达到出色的算法性能并不容易。

3.2 基于核函数的流形学习方法

黎曼流形与向量空间(欧氏空间)的最大区别在于，欧氏空间具有简单且容易理解的数学特性，如欧氏距离、范数、向量内积等。在计算机视觉领域中的许多以欧氏空间为几何基础的算法中，对于核函数方法的使用也取得了不错的效果[45-46]。因此，完全可以通过类似方法，将黎曼流形嵌入到高维的重构核希尔伯特空间(Reproducing Kernel Hilbert Space，RKHS)中。此高维空间可以看作是一个无穷维的线性空间，因此许多欧氏空间中的算法均可被直接应用到RKHS空间中，这是由于RKHS空间也具有向量空间的重要几何特性——内积。虽然RKHS空间具有良好的几何结构，但如何将流形空间嵌入到RKHS空间是最重要的问题，即如何找到合适的、定义在黎曼流形上的映射核函数，进而把流形空间的非线性结构映射到无穷高维的重构希尔伯特空间中，以将线性空间中的算法拓展至流形空间。

对于流形上的映射核函数，文献[47]使用了SPD流形上的核函数，并将其与局部保留映射(Locality Preserving Projections)方法进行了结合，其使用的映射核函数是根据仿射不变距离推导的。文献[48]提出了SPD流形上的核稀疏编码方法，其使用的映射核函数为高斯映射核函数；在文献[49]中，映射距离核函数及其变型被应用于Grassmann流形的分类问题。根据Mercer定理，核函数必须是正定的。然而，尽管许多正定核函数在欧氏空间下具有很好的效果，但是当将同样的正定核函数应用于流形数据时，效果却并不理想。因此，对于流形上的核函数方法而言，关键点在于找到适合的映射核函数形式。

3.3 基于深度学习的流形学习方法

近几年来，在计算机视觉和机器学习领域的各种任务中，深度神经网络的性能表现远超传统的浅层学习网络。正是由于深度学习在计算机视觉、自然语言处理和人工智能等在内的多个领域的广泛应用中取得了空前的成功[50-56]，最近几年，研究者们将深度学习与黎曼流形进行了结合，以充分发挥深度神经网络在解决涉及几何结构的相关任务中的潜力[57]，并提出了一些新的代表性方法，包括测地线卷积[58]和矩阵反向传播方法[59]。基于这些工作，越来越多的新型神经网络建立在非欧空间中[60-65]。例如，文献[60]通过图傅里叶变换提出了一种面向图数据的变形卷积网络，并定义了一种图拉普拉斯算子，进而将拉普拉斯算子推广到了图数据上。之后，文献[64]在空域-时域图上提出了一种深度学习方法。该方法将空域-时域图看作是一个前向的递归混合网络。文献[65]在正定对称流形上构建了深度网络，同时将该网络通过矩阵反向传播方法进行了训练。

流形上的深度学习网络建立在矩阵反向传播框架[59]的基础上，进而将传统的向量数据间的梯度计算推广到了流形数据。在这一理论框架中，一些现代矩阵分析方法(包括矩阵链式法则及矩阵微分原理等)同样是必不可少的工具。在这些理论基础得以发展的前提下，文献[66]提出了在正交限制条件下处理矩阵数据，进而将数据空间转换到Stiefel流形上。该方法在卷积神经网络框架下，为网络后端的参数空间赋予了正交结构，进而达到了优化参数空间的目的。在之后一系列的相关研究中，在传统神经网络中基于向量结构的操作(如卷积、池化、标准化等操作层)也针对流形结构数据进行了重新设计。对于卷积操作而言，文献[64]提出了测地线卷积这一概念。该方法能够在诸如姿态识别任务中建立形状对应性和恢复形状时发挥优势。然而，仅仅经过改进的神经网络层不能直接扩展到流形数据以支持流形上的深度学习方法，因为这其中的大多数操作(如线性或非线性变换等)均无法保留流形的几何结构。为了在深度网络的学习过程中保持流形几何结构，目前现存的方法主要可归为两类：第一类是基于流形几何结构的内蕴方法，另一类是基于映射的嵌入方法。二者的主要区别在于是否需要将黎曼流形嵌入到一个更高维的欧氏空间中。对于不同的黎曼流形而言，相应的内蕴方法也有所不同，这是因为不同类型的流形具有不同的几何结构。对于第一类方法而言，文献[65]以正定对称流形作为输入，根据正定对称流形的几何特性，设计了正定对称流形上的映射层、特征分解层、对数映射层等，进而实现了正定对称流形上的深度学习。文献[61]以Grassmann流形作为输入，通过转换层、正交化层、映射层等学习了分类能力更强的流形数据，之后再将流形数据嵌入到欧氏空间，最后接入softmax层进行识别，进而实现了Grassmann流形上的图像集识别网络。第二类方法基于外部空间映射的思想，通过将黎曼流形上的数据映射到切空间中，从而把流形空间中的深度学习问题转换为向量空间中的深度学习问题。由于流形上某点的切空间是向量空间，传统深度网络中的各种常规线性操作层则可在切空间中进行计算。换言之，可以训练常规的深度神经网络来学习从数据的输入空间(即欧几里得空间)到黎曼流形切空间的映射，之后再通过黎曼对数映射将数据从切空间拉回到流形空间。总体而言，基于流形的深度学习网络在视频/图像集分类、表情分类、动作识别、精细图像分类等领域中都取得了出色的表现。

3.4 黎曼流形学习方法的未来发展趋势

近几年来，随着深度学习方法的火速发展，现阶段对于黎曼流形学习方法而言，既是机遇，又是挑战。黎曼流形学习方法在计算机视觉中的发展，趋于如下几个方向：

(1)将黎曼几何嵌入深度网络：近年来，人们对基于黎曼几何的深度神经网络越来越感兴趣，并且认为该方向有可能成为提高深度学习准确性和鲁棒性的主流方法。在这个方向上，黎曼流形学习技术将起到关键作用，因为通过该方法，数据的结构信息可被嵌入到网络中。尽管取得了一些初步进展[67-68]，但基于几何的深度神经网络意味着网络几何结构上的转换，其中仍然存在许多挑战，例如通过对黎曼流形进行正则化来克服过度拟合问题，为非欧结构层设计更为有效的优化方法，以及如何从真实世界数据集中获取几何特征等。

(2)几何深度学习：即对具有几何结构的数据进行深度学习的方法的研究，该领域代表了深度学习领域的新趋势之一。这些具有几何结构的数据不仅包括图像/视频，还包括其他类型的数据，如黎曼结构数据、三维立体目标数据、图结构数据和社交网络数据等[67]。

(3)鲁棒机器学习：机器学习方法模型的一个最显著的弱点是其容易受到恶意对抗性干扰的影响，对抗性攻击对诸如深度神经网络之类灵活性较强的模型而言更是如此。这些对抗干扰会误导模型做出错误决策[69-70]。研究表明，Grassmann流形学习方法对于小扰动表现出了一定程度的鲁棒性[71]，最直观的原因是小扰动很难将一个子空间更改为另一个子空间。 因此，如何利用Grassmann流形及其他黎曼流形设计出鲁棒性更强的机器学习模型，具有重要的研究价值。

4 结 论

数据几何结构的重要性是不容忽视的，即便如此，传统方法仍然通常将数据在向量空间中进行处理。然而，黎曼流形方法可充分利用数据的几何结构，从非欧几何角度入手设计和优化学习模型，在计算机视觉领域的诸多任务中往往能获得更好的学习效果。除了从学习模型的优化角度考虑，视觉任务中数据的黎曼结构特性也使得黎曼学习方法成为了解决相应任务的关键手段。对于近年来备受瞩目的深度学习技术而言，如何巧妙地将黎曼流形方法与深度学习方法相结合，进而为解决深度学习方法在模型训练、模型设计及模型可解释性等环节存在的相关问题，提供了一个强有力的工具。