运用图示培养学生的计算素养

张海兰

[摘 要]计算素养的培养是小学教育研究的热点。在小学数学教学中，运用图示解题是一类重要的思想方法，它能够帮助学生理解运算的本质和运算规律。教师应积极探究图示在小学数学教学中的作用，合理运用图示培养学生的数学计算素养。

[关键词]小学数学;图示;计算素养

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2020）35-0084-02

图示就是图形和数字相结合的形式。图形被作为辅助手段去表达数，数又作为表现手段去表征图形，这便是数和形之间的关系。数和形之间是辩证统一的，教师运用图示可以很好地培养学生的数学计算素养。

一、运用图示理解计算本质

多数数学教师在教学计算的算理时，没有带领学生深入探讨计算的本质，而是直接告诉学生计算法则后，便开展相关习题的训练和讲解。如此，学生便是机械地接受知识，这不仅会增加学生对计算的抵触心理，还有可能在今后的学习中因为对算理、算法理解不到位造成计算错误。而利用图示不仅能降低理解知识的难度，还能引导学生理解计算的本质。

以“分数的认识”的教学为例。

师：有2个小朋友都想吃月饼，可是只有1个月饼应该怎么分呢？

生1：我觉得应该一人一半。

师：一人一半是什么意思呢？是把一个月饼随便掰成两半吗？

生1：是的。

（教师故意把一个月饼掰成了一半大，一半小）

师：这样也可以吗？

生2：不对，应该保证每个小朋友分到的月饼是一样大的。

师：如果把这个月饼平均分成2份，每个小朋友拿1份，那每个小朋友拿的份数是总体的多少呢？

生3：1/2，意思是每个小朋友都分得一半。

师：同学们能够用图形表示出来吗？

（如下图，学生在草稿纸上画了一个圆，将这个圆一分为二，其中的一半表示1/2）

师：现在请同学们画出2个完全相同的圆，一个圆给小红，另一个圆给小明，那么一个圆又是整体的多少呢？ [小明得到的圆][小红得到的圆]

（教师见同学们没有思路，就又举了一个例子）

师：现在有2个月饼，不用把月饼分成两半，每个小朋友都拿到了1个月饼，那么这也算是平均分吗？

生4：算。在这种情况下一个圆就表示1/2，但刚才那种情况一个半圆也是表示1/2。

师：分数表示的是一个比例的关系。我们不能只关心一部分的数量大小，要两部分对比着看。不管数量是多少，如果一个人分得的份数是总的份数的1/2就表示平均分。

在学生不理解时，教师通过举例子和画图的方式引发他们思考。经过以上的探讨，学生能正确地理解“1/2”的含义，知道“1”和“2”分别表示什么，如此学生对于分数本质的理解更为深刻：将单位“1”平均分成若干份，取其中的一份或几份就可以用分数来表示。学生今后在学习分数的加、减、乘、除时，便不容易犯错误。

二、运用图示归纳运算方法

小学生的计算速度比较慢，还很容易出错。而计算是极其讲究技巧的，使用便捷的运算方法，不仅能够提高计算速度，还能够保证计算的准确率。因此，教师可以借助图形让学生找到归纳运算的方法。

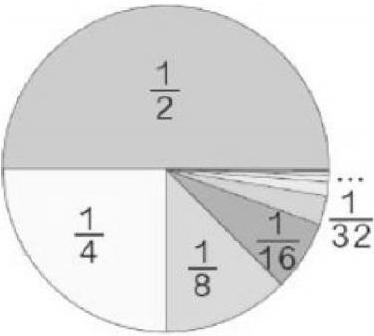
师：请同学们计算1/2+1/4+1/8+1/16+1/32+1/64+1/128+……=？

生1：这个式子也太长了，应该怎么计算呢？

生2：我觉得这么长的式子应该有特殊的计算方法，不然我们没有办法计算呀。

师：同学们不妨先仔细观察一下，看看能否找到一些规律。

生3：后一个数的分母是前一个数的分母的2倍。

师：然后呢？

生4：我先一个一个加下去看看，看看能否找到一些规律，1/2+1/4=3/4，3/4+1/8=7/8，7/8+1/16=15/16，15/16+1/32=31/32……这样计算实在是太麻烦了，还非常容易出错，这道题目不能得出答案！

师：请同学们观察计算结果，你发现了什么呢？

生5：我发现式子的答案越来越接近1，会不会最后的结果就是1呢？

师：如何验证你们的猜想呢？

生6：可以画个圆来分析，先画出一个圆表示单位“1”，再将这个圆平均分成2份就可以得到1/2，1/2平均分成2份就可以得到1/4……总之就是标记出整个圆的1/2，1/4，1/8，1/16，1/32……发现这几部分的面积加起来越来越接近整个圆的面积。继续分下去，总和就是1。

可见，图形能够帮助学生找到一些计算的思路。今后在教學异分母分数相加减时，教师可以借助图形让学生把理解两个分母不同的分数进行通分是因为一个圆有很多种划分方式，让两个本来以不同方式划分的圆调整为用同一种方式划分，这样就可以实现分母不变，分子相加减的运算。借助图形，学生便能够总结出异分母相加减的法则，而且能够形成较深的记忆。因此，教师在教学时应当仔细研读教材，找寻图示的优点，向学生推广用图示解题的方法。

三、运用图示显现运算思路

学生要从低年段迈入高年段。这时，算法的考查形式也会发生变化，不再是让学生直接计算算式，而是以一个题目为背景，让学生找寻数量关系，然后计算求解。在包裹上问题的外衣之后，很多学生难以找寻正确的运算思路，导致解题时处处碰壁。此时利用图示可以简化题目中的数量关系，降低计算的难度。

师：小林、小强、小芳、小兵和小刚5人进行篮球比赛，每两个人比一场。小林已经比了4场，小强比了3场，小芳比了2场，小兵比了1场，请问小刚一共比了几场？分别是和谁一起比赛的？

生1：小林总共比了4场，他分别和小强、小芳、小兵、小刚进行了比赛。小强比了3场，他分别和小芳、小兵、小刚进行了比赛。小芳比了2场，他分别和小兵、小刚进行了比赛。小兵比了1场，其和小刚进行了1场比赛，所以小刚也只和小兵进行了1场比赛。

师：你们认为他说的对吗？

生2：题目中说每两个人比一场，小林和小芳比了1场，那么小芳也应该和小林比1场才对。这位同学说小芳只和小兵、小刚比了2场，所以我觉得是不对的。

师：这道题目看起来有点难，我们可以用连线的方式进行分析。在草稿纸上分别写出小林、小强、小芳、小兵和小刚。小林总共比了4场，那么就把小林分别和小刚、小兵、小芳、小强连起来;小强总共比了3场，我们不妨把小强和小林、小刚、小芳连起来;小芳比了2场，这时已经不用再添加线段了;小兵比了1场，也不用添加线段。这时已经完全符合题意，从图中我们可以看到小刚只比了2场，他分别和小林、小强进行了比赛。

生3：以后当我们读不懂题的时候，不妨把题目中的信息转换为图示，没准我们就能够找到解题的思路。

像这样，使用图示便很好地解决了这道题。另外，在传统的鸡兔同笼问题中，很多教师也采用了图示的方法，让学生找到计算的思路。图示相比于文字，更为简洁和直观，学生也很容易看出数量之间的关系。从某种意义上来说，图示是文字的简化，有时利用图示分析问题会收获事半功倍的效果。

总之，数和形是数学中最基本的素材，两者在一定条件下可以相互转化，相互结合，这便是图示思想的由来。总的来说，图示思想在小学数学教学中应用得比较广泛，因此，教师在教学中要大力推广它，让学生在学习中正确运用。

[ 参 考 文 献 ]

[1] 李建坤.图示培养小学生“学会学习”的素养[J].福建教育学院学报，2018（05）.

[2] 蔡玮，袁仕芳，罗丹丹.基于小学数学核心素养的图示教学研究[J].考试周刊，2018（31）.

（责编 黄 露）