基于GNSS数据处理中基线解算及分析提高基线解算质量

王鹏飞 王子烨 杨能榜

（石家庄铁道大学土木工程学院 河北省石家庄市 050043）

1 基线解算介绍

基线的选取和解算过程是解决精度不够问题的核心步骤，它的选取对保证最终数据质量和精密度起着至关重要的作用。在此过程中，无论是卫星还是接收机，它们在信号传输过程中还有地面位置偏差方面都可能产生误差，解算的主要误差来源主要包含三个：卫星的星历误差、电离层对传播过程产生的误差影响、对流层折射相对误差。下面讲解的基线解算，其步骤大致包括原始数据的读入；外业数据的检查与改正：基线解算参数的设定这三个主要步骤。

2 基线解算模式

（1）基线的向量解算。

完成基线的解算先要对接收机之间建立起联系，完成这个联系的建立需要利用两台或两台以上的接收机，接收机通过接收到的卫星发射回的数据信息，对收集到的观测数据进行差分处理，处理后的数据会形成不同的差分，最后引入参数估计的数学方法，对接收到的数据引入算法进行解算，以此来解算出接收机之间X,Y,Z 的坐标差，通过建立起坐标系统，最终得到我们通过GNSS 测量所想获取的坐标点位置信息，这就是我们通常所说的获取的地面上的相对坐标。如图1、图2、图3 所示。

（2）单基线解算，基线向量估值：

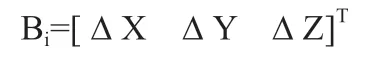
（3）多基线解算。

如图4 和图5 所示。

（4）基线向量估值：含有 m - 1 条函数独立的基线向量：

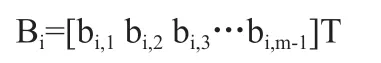
3 GPS基线解算过程中误差分析

影响基线解算质量的主要因素有：

（1）卫星在上方的位置不准确存在偏差；

（2）电离层使得传播的过程存在延迟，导致了误差产生，以及对流层延迟可能造成的误差；

（3）多路径效应和接收机噪声。

主要介绍以下几种常见导致误差存在的原因：

3.1 卫星星历误差

卫星在太空运行中会受到不同作用力的影响，我们称这种力为摄动力。但由于这摄动力规律性较差，地面监测站对其很难实现有效的监测，对其受到作用力的规律也难以做出判定分析，导致其对星历的预报存在误差。

3.2 电离层折射误差

我们所说的电离层是指在距地表100km 以上1000km 以下的高度，由于太阳的辐射作用，大气会在电离层中发生电离，从而产生不同种类的离子，与此相似的是卫星和接收机之间发射、传递的信号，它们在通过电离层时，会发生相同的情况，导致信号原路径与传播速度发生变化，直接导致信号的传播产生误差。

图1：基线边长（AB 间距离代表边长）

图2：基线的向量表示方式

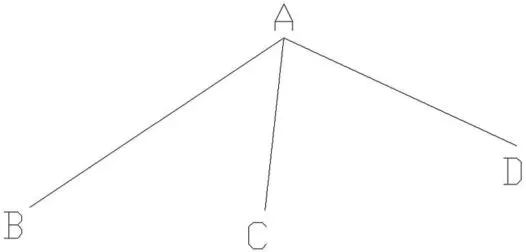
图3：具有共同端点同步观测基线法

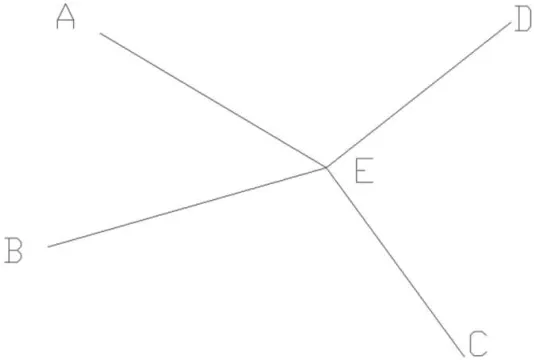
图4：射线法

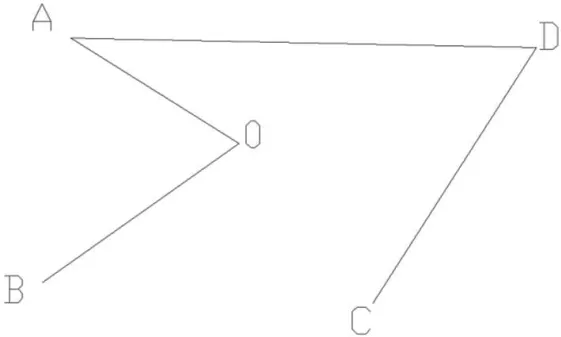
图5：（方向：B-O-A-D-C）导线法进行解算

3.3 对流层折射误差

对流层是高度大约为40km 范围的大气底层，由于受到地面辐射的影响较大，当卫星的信号在穿越对流层时会有一定量损失，这是折射现象产生的根本因素，我们对传播过程中产生的误差称为对流层的信号延迟，在信号传递过程中传播路径会因此改变，导致最终测量结果产生误差。

4 提高基线解算质量的措施及解决效果分析

（1）为保证好基线质量的控制工作，在通过卫星和接收机获得的最终数据剔除率需满足精度要求，为避免组成的同步环中存在带有误差的基线向量，应保证基线中坐标分量同步环闭合差满足以下条件：

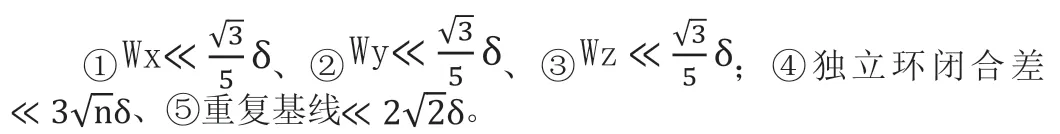
（2）“摘星”的处理（剔除误差较大的卫星）从卫星中获取的数据信息来看，所得数据质量与卫星观测的时间有很大关系。为解算出卫星的观测参数，需要保证卫星的观测时长不可以过短，由于观测时间短的卫星，其观测数据准确性不足，不可将其产生的数据参与基线结算，最终解算的质量无法保证，数据不具有参考的意义。同样道理，在某一观测时段中，若“周跳”这种现象频繁的发生，将会导致数据无法准确修复，根据此情况，可对卫星周跳发生严重的卫星进行删除，剔除相应卫星所测得的数据，其中大致包括以下两种情况：①同一时间段内多个卫星存在周跳现象，卫星群的数据信息极不稳定；②单个卫星在某时间段中频繁发生周跳现象，单位时间内发生“周跳”情况严重的卫星数据应给予剔除。

（3）电离层通过改正模型减少误差。在理想状态下，接收机接收卫星信号的路径是从卫星直接到接收机天线。但这种只是非常理想的状态，在真实的传播中信号的传播一定会发生一些延迟，产生误差，但这种误差并不是无法解决，对于电离层对无线电信号的延迟，可通过确定精确的电离层延迟信息(电离层模型)，对于单频GPS 用户可以满足高精度改正电离层延迟影响的需求，便于GPS 用户进一步提高测量精度的要求。

（4）改正模型的引入。当两观测站间距离较小，在不受地球曲率的影响下，卫星信号在电离层中的传播效果与在对流层中的传播效果较为相似，我们可以将电离层中信号的传播近似的认为成卫星信号在对流层中的传播。在我们将这种理想状态下的情况引进改正模型时候，根据这一项特征可求出卫星的同步观测值之差，通过差值间的比较分析找到误差的来源和解决方式，能较好削弱对流层折射产生的影响。

（5）案例情况分析：我们采用8 条基线，4 个同步的闭合环，在不同时间段进行多次观测，采用双星解算+电离层模型+精密星历共同组合处理的效果，我们可以得到广播星历下解算和精密星历下解算这两种解算的结果，我们不难发现GPS+电离层模型的效果要优于仅用GPS 解算，但是超限同步中有些情况不是可以通过电离层的模型进行解决的，当我们对数据的处理使用双星来解算时，对所有基线中存在问题的基线可和 同步闭合差的改善有着明显的效果，因此我们可以认为，在双星解算的基础上加上电离层模型的解算效果并不明显，对数据的改善并不大。

当我们将精密星历引入解算中时，我们可以发现其解算处理的结果与广播星历解算的结果大致相同，这就可以证明出当我们引入精密解算星历，即使对精度的提高并没有起到很大的改善作用，但是对结果不会产生不良影响，并且会随着基线长度增加，对解算结果产生的影响也更明显。

5 解决提高质量方法的总结

在测量中，目前我们用到的主要是精确测定基线的长度或水平控制网中的起始边长的技术和方法，一般我们所讲的基线是指在测量工作中作为起始标准的线段，对于GNSS 基线解算中产生误差的因素包含很多，首先要对解算的过程进行分析，基线向量是GPS控制网的基本单位，GPS 控制网的优劣主要依赖基线精度的高低。综上述内容所叙述，大致可采用以下几种方式来解决基线精度不够的问题：

（1）通过增加高度截止角（一般默认的角度为15 度），可使接收机接收到质量更好的信号，使得卫星与地面之间的信息输送更准确。

（2）对卫星观测组合方案进行调整，卫星群中的“子卫星”位于不同的空间坐标位置，我们可以对其原有的位置进行改变与重新组合，选择不同的观测组合方案可提高精度。我们目前所讲的GNSS 卫星导航定位系统包含着多个国家的不同系统，因此卫星之间的不同组合，不同位置势必会对观测数据误差带来相应的影响。因此合理的位置和组合方式对测得数据的精度提高具有很强意义。

（3）通过改变卫星组合中卫星的数量或重新选定新的参考卫星，对不同卫星数量获取到的数据做出分析比较，从而确定出最佳观测卫星的数。

（4）进行“摘星”处理，将参差较大或某时间段内发生“整周跳变”的卫星取消使用，参考使用参数变化小且稳定的卫星。由于在不同的时间段内进行观测，卫星随着位置的移动会对所测得数据带来一定的影响，我们需要综合考虑不同时间段、不同的观测位置以及不同型号卫星所测得的数据差异，进行一个“取舍”，使得我们最终使用的卫星精度要求最高。

对于平常的基线解散过程中，先对基线产生误差的原因进行系统的分析，一般产生误差的原因来源于接收机和卫星，因此为了解决问题和提高精度，我们应该综合分析多种可能存在的因素，针对于卫星之前所得到的数据，再根据实际情况采用改变观测组合，选择性删除卫星等不同的方法来提高基线的精度；在提高基线的精度后需严格依据相关规范，对基线的质量控制进行分析，包括数据剔除率，同步环、独立环闭合差等要求，最终得到满足精度和各项要求的高质量高精度基线。