计算机网络优化设计中遗传算法的原理及应用

由睿鹏

（黑龙江省军区 黑龙江省哈尔滨市 150001）

在现代计算机技术与网络技术的飞速发展中，硬件设备层面的安全可靠性已经能够得到良好保障，所以在硬件运行状态稳定的情况下，需要通过软件算法的改进来对计算机网络进行进一步优化。因此，计算机软件算法将是计算机网络未来发展中的研究重点。目前，人们已经在尝试将各种算法应用到计算机网络优化当中，遗传算法就是其中之一。该算法具有诸多优势，可以帮助网络系统找到全局最优解，从而提升网络系统整体的可靠性。因此，加强该算法在计算机网络优化设计中的应用是尤为关键的。

1 计算机网络及其特点

计算机网络主要是由不同区域独立计算机及外部设备在连接线路与交互设备的连接下构成的一种网络系统，其通过网络协议、管理软件等的协调，可以实现网络内部的信息共享并具备特定功能。在计算机网络中，每个独立设备都能够共享网络中的资源，但却不能对整个网络进行控制。实际上，计算机网络中的各设备是可以相跨较大的空间跨度的，这是其主要特点之一。此外，计算机网络信息资源的传输主要依靠通信链路与传输设备，同时其资源共享等功能也需要借助管理协议与软件等来实现。具体分析计算机网络的整个组成，其大致包含三部分，即服务器、传输设备、软件。而计算机网络在搭建时，还需要有一套基本的结构，即各种硬件连接后所形成的基本构造形态。目前计算机网络构建时采用的基本都是拓扑结构，只是在该结构的设计上需要满足用户、施工、兼容、扩展、升级等各方面要求，以保证网络搭建的科学合理性。而在计算机网络搭建完成后，其网络的进一步优化，则需要依靠软件算法的改进来完成，所以在现代网络发展中，计算机网络设计时算法的优化改进同样是其研究重点之一。

2 遗传算法及其基本原理

2.1 遗传算法及其特点

所谓遗传算法，就是数学领域用以通过计算找到最佳解决方法的一种搜索算法，其归属于进化算法。该算法最早是从生物界的进化规律上演化出来的，随后被计算机科学所应用，成为计算机领域中进行搜索和优化的机制。该算法的具体流程如图1所示。首先，该算法的应用需要先在现有模型的基础上来对需要求解的问题进行编码并生成随机遗传群，再通过针对选择概率与适应函数的一系列选择性复制、交叉、变异来对其最终解的适应性评估满足情况进行验证。若经过验证其最终解满足迭代收敛要素，则说明该解是最优的，反之则需要继续重复以上步骤直至找到最优解。

目前，计算机网络优化设计中已经开始大量应用遗传算法，其原因就在于遗传算法能够通过自然选择来进行全局随机搜索，进而从计算机问题中找到最优的解决问题的方法。与其他算法相比，遗传算法的特点主要体现再以下几方面：

（1）其操作对象为参数编码而非参数本身；

（2）能够实现多点同时搜索；

（3）该算法的运用需要利用数学相关函数来进行评价方法的确定；

（4）算法计算中需要遵循最优化原则，以实现对全局最优解的搜索。

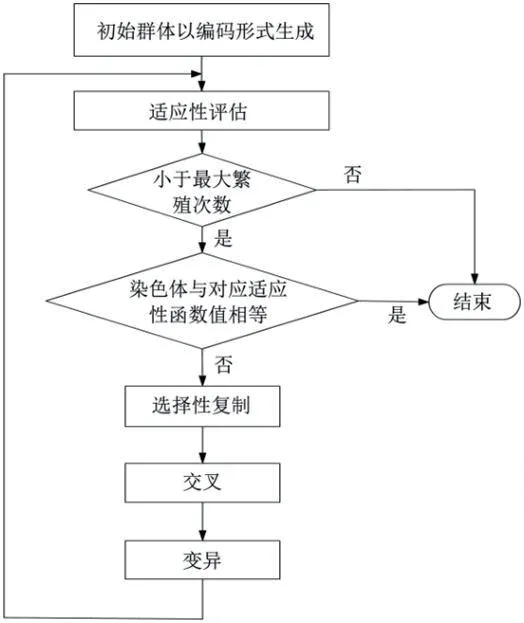
图1：遗传算法流程

遗传算法的这些特点，也使得其具有了许多明显优势。首先，遗传算法由于不以参数本身为操作对象，所以能够规避掉许多约束条件，从而使得该算法在计算机网络的更多方面得以应用。其次，其多点同时搜索的特性可以实现更大范围内的搜索，打破传统算法的局限性。再次，该算法的评价方式确定与辅助信息关联甚少，所以其对问题本身的依赖度较低。最后，遗传算法不依靠确定性规则进行搜索，所以其搜索可以扩展到全局。正是遗传算法的这些优势，使得其正在帮助现代计算机网络解决许多难点问题。

2.2 遗传算法的基本原理

遗传算法的数学表达方式下所示：

其中P0代表初始成员集，使一种编码形式，λ 代表集体成员数量，L 代表编码长度，Z 为非负整数的集合；代表最终解的编码是由0 与1 两种元素组成；s 代表选择性复制；c、m 分别代表交叉与变异；T 则为最终的算法结果。如果T=1，则说明找到最优解，如果T=0 则说明该解不是最优，需进一步进行计算以找到最优解。

3 计算机网络优化设计中遗传算法的应用

3.1 计算机网络优化的基本原则

现代计算机网络运行越来越强调安全稳定性，所以在进行计算机网络优化设计时，首要遵循的原则就是可靠性原则。

计算机网络的可靠性体现在其能够在指定时间与范围内完成相关任务，期间不出现问题。要达成这一目标，网络优化设计需要集中于网络运行层面的安全可靠性上。网络运行的安全可靠又进一步体现在网络稳定性与故障的发现和解决上。针对网络稳定性，其优化设计中通常需要通过计算机网络模型概率来发现网络中的问题，以提升网络可靠性。而计算机网络的故障发现与解决还需要通过软件算法的优化来予以保障，这就是当前计算机网络领域进行算法改进的根本所在。因此，遗传算法在计算机网络中的应用正是基于这种可靠性原则而开始的，所以其在计算机网络优化设计中的应用也必须将这一原则作为基础。

3.2 基于网络可靠性优化的遗传算法改进

遗传算法在基于网络可靠性的网络设计优化中因其自身优点而常常被作为解决多个局部极值优化与高维搜索问题时的首选。然而从遗传算法的基本原理可以发现，其寻求最优解的过程可能较为漫长，所以在基于可靠性进行计算机网络优化设计时，也需要对遗传算法进行改进。如可以在传统遗传算法的繁殖过程中引入竞争繁殖，使该算法不但可以与其他优化方法进行衔接，更可以继续保持初始解的分散性。这种改进能够让遗传算法在解决长编码问题上有更高效率。其具体改进方法如下：

传统繁殖过程的表达式如公式3所示。

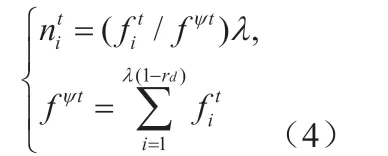
该表达式中的rd就是改进后所引入的淘汰率。

3.3 基于遗传算法的计算机网络优化设计具体过程

首先，要明确其优化设计的基本准则。一是要对计算机网络的拓扑结构进行合理选择；二是要确保网络的容错能力与冗余性；三是要尽可能选择开放性的网络体系结构；四是要尽可能使用先进网络管理软件；五是要对网络系统进行最优配置。

其次，确定优化设计的具体数学模型。根据计算机网络的特点，在优化设计中，信息处理需要采取先来后到的顺序。同时针对计算路由选择与链路容量分配时的容量成本和传输成本，就需要建构出一套基于可靠性的网络优化数学模型。如网络可以按照树状网络形式布置，再利用遗传算法对其进行优化设计。计算机网络通常有M条待选链路与N 个节点，在依靠遗传算法进行优化时，其各种问题是以编码形式进行描述的。优化设计过程中需要进行网络中随机待选链路的选择，并将对其节点连通性进行判断。如果运用遗传算法搜索到N 个节点，则该链路是畅通的，其中N-1 条链路组成一个完整网络。此处在构建数学模型时，可以将网络拓扑结构假设成A（S，D），其中S 代表节点集合，D 代表链路集合，则其链路成本的成本计算如公式（5）所示：

设Xpq=1 代表pq 之间连接，Xpq=0 代表其他，则该问题的解集为（X12，X13，•••，X1n，X23，X24，•••，X2n，•••X（n-1）n），其链路成本为（Y12，Y13，•••，Y1n，Y23，Y24，•••，Y2n，•••Y（n-1）n）。同时据此可构建出的数学模型如如下所示：

模型中的T（X）代表网络可靠度，Tmin（X）代表在进行优化设计时所必须要满足的可靠性要求。此外，运用该模型进行优化时，还必须按照以下约束条件来进行。一是保证网络连接畅通，二是节点最大连接数量不能超过H，三是链路成本最低。

最后，根据改进后的遗传算法对网络进行优化设计。其具体流程为：

（1）利用二进制方法来编码初始群体，用以表达遗传基因；

（2）对种群个体成本进行计算，同时完成排序。然后以f（x）=（x-1）/（Ps-1）作为适值函数（Ps 代表种群大小）；

（3）利用适值函数来挑选种群的规模，进而将小概率种群基因淘汰掉，其概率选择公式如公式5所示；

（4）在网络畅通的基础上利用改进后的遗传算法实施网络节点优化，以找到基因交叉位置并得到最优解；⑤在达到最大设定迭代次数前持续进行迭代计算直至能够保障计算机网络可靠性的最优解出现。

3.4 搜索方式的确定

在计算机网络优化设计中，网络搜索优化也是遗传算法的应用邻域，以通过遗传算法来都得更高精度、更高收敛速度的搜索方式。而这种搜索方法的确定，需要立足计算机网络中各种主要问题的解决上，通过收敛速度的提升来提高网络中的搜索效率，通过精度的提升来提高其搜索质量。因此，在利用遗传算法对其搜索方式进行优化的过程中就需要将收敛速度与搜索精度作为两项关键评价标准。

虽然遗传算法具有应用简便、易于操作等优点，但由于遗传算法在实际应用中容易局限在对局部进行最佳优化上，所以在计算机网络优化设计中也需要通过对搜索方式的优化来提升运用遗传算法所进行的搜索速度。目前，人们常常会在应用遗传算法时选用启发式搜索算法，这是因为该算法通用性较强，可以在各种网络的优化中都有效适用，同时其还可以与遗传算法进行有效结合，使得计算机网络运行中可以利用两者进行邻域解的对比，从而使遗传算法可以在运行中始终在优化解的方向上不断进行搜索。

4 结语

通过上述遗传算法的改进和具体的计算机网络优化设计过程，可以紧紧围绕可靠性原则求得计算机网络全局的最优解，进而最大程度上提升计算机网络系统整体的安全性。但在遗传算法的应用中，其算法改进同样是十分关键的。所以随着现代计算机网络的不断发展，加强遗传算法的研究仍是有必要的，这就要求相关人员结合新时期计算机网络运行的实际情况来不断探索遗传算法在其网络优化设计中的应用，以不断提升现代计算机网络系统的安全可靠性。