线性加载作用下软土地基固结变形分析
2020-02-03杜明芳满景奇孙运德
杜明芳, 满景奇, 孙运德
(河南工业大学土木建筑学院, 郑州 450001)
随着中国对基础建设的不断投入,在许多的工程中要面临软土地基在线性加载下的固结变形问题,如高层建筑、滩涂围垦工程建设等,由于太沙基一维固结理论,适用于瞬时加载,不能分析缓慢加载过程中软土地基的固结变形特性,因此充分认识到软土地基在线性加载下全阶段的固结变形特性,具有实际工程意义。有些学者用不同的方法求解了加载下的固结解[1-5];淦方超[6]通过对各固结理论进行参数敏感性分析,确定了影响固结结果稳定性的主/次要参数;梅国雄等[7]通过一维固结理论证明了在线性/近似线性加载下沉降随时间对数变化曲线呈S形; 张绍勇等[8]基于砂井轴对称固结模型推导了线性加载下不排水桩复合地基径竖固结解析解;黄朝煊等[9]基于同焦椭圆柱理论和等应变假设,推导了塑料排水板地基在线性加载下固结解析解,并通过已有的有限元计算及数值计算结果进行对比验证;张子培等[10]通过灰色理论推导了一种分级加载下地基沉降预测方法,并结合工程实例进行分析;赵明华等[11]通过考虑初始应力与附加应力随深度线性变化时求解的双曲线一维固结方程发现时间因素不适合作为描述时间的无量纲因子;李冰河等[12]在初始有效应力沿深度变化的条件下求解了软黏土非线性一维固结解;秦亚琼[13]基于曲线拟合一遗传算法联合建模的方法对工程实例进行沉降预测,发现预测值和实测值较为吻合。
从以上学者的研究可知,目前中外对线性加载下软土地基全阶段的固结变形特性研究较少。基于太沙基一维固结理论,推导出任意加载速率下的一维固结方程的通解,并给出了线性加载下固结方程的解析解。并将实际监测数据与理论值进行对比,验算该方法的合理性,以期为实际工程沉降及工程使用维护提供参考。
1 加载作用下软土地基的一维固结方程
1.1 太沙基一维固结理论
图1表示饱和的软土层,其厚度为H,并且在自重作用下已完成了固结。设土层表面受到均布荷载q的作用,由它引起的附加应力σz沿深度均匀分布,如图1中BE线所示。饱和软土层上部是透水砂层,下部是坚硬的不透水层,在固结过程中,土中的水只能从上面的透水砂层中排出。BD表示任意时间t土中有效应力σ′和超静孔隙水压力u沿深度z的变化曲线,如图1中的虚线所示。有效应力σ′和孔隙水压力u为深度z和时间t的函数,分别以σ′=σ′(z,t)和u=u(z,t)表示。即孔隙水压力u=u(z,t)的微分方程式[14]为
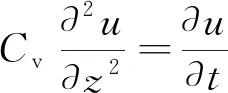
(1)
式(1)中:Cv为表示土体固结速度大小的系数,m2/s。
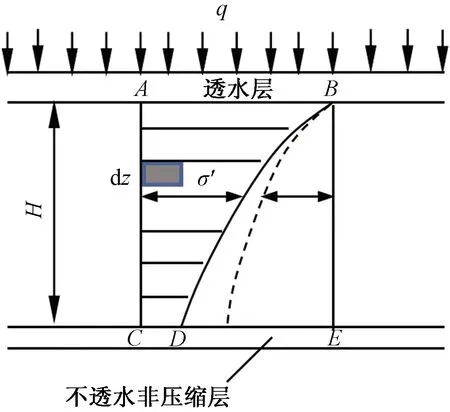
图1 太沙基一维固结理论计算简图Fig.1 The calculation diagram of the one-dimensional consolidation theory of K.Terzaghi
太沙基一维固结理论的基本假定有以下几点:①假定体是均质且完全饱和的材料;②土体发生的变形完全是由于孔隙水压力消散引起的;③土中水的渗流服从达西定律,方向和土体压缩方向均为竖向(一维)的;④外荷载均布、连续并且是瞬时加载,当t=0时,附加应力σz完全由孔隙水压力u来承受;当t=∞时,附加应力σz完全由土骨架来承受。
1.2 加载下计算简图及相关假定
图2中作用的荷载假定为大面积的均布荷载,与太沙基一维固结理论假定相比,除作用在软土上的荷载情况外,其余条件都与太沙基一维固结理论假定相同。
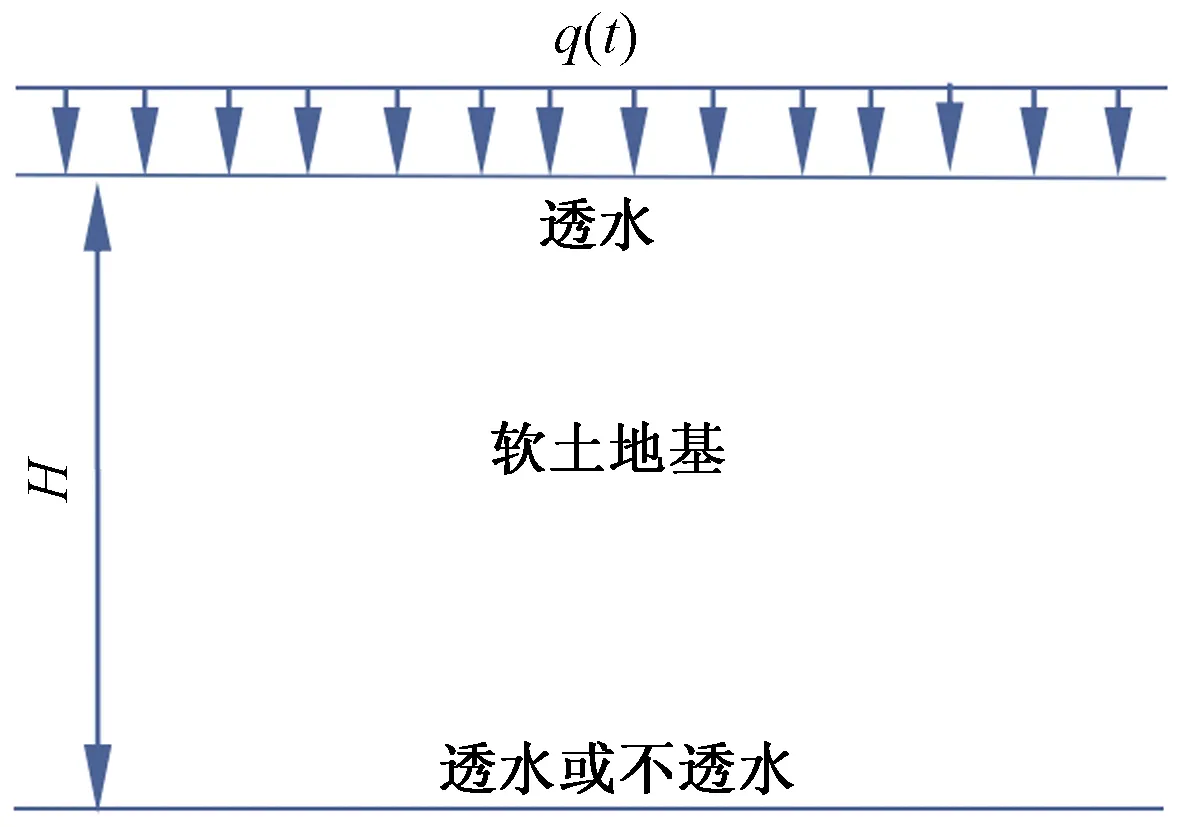
图2 加载下一维固结计算简图Fig.2 The calculation diagram of one-dimensional consolidation of load
可推得软土地基在任意加载速率下的一维固结基本方程[14]为

(2)
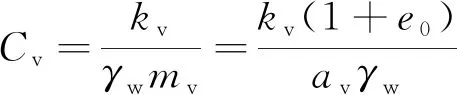
(3)
式中:f(t)为加载速率,f(t)=dq(t)/dt,kPa;kv为土的渗透系数,m/s;mv为土的体积压缩系数,kPa-1,mv=1/Es=av/(1+e0),其中Es为土的压缩模量,kPa;γw为孔隙液体重度,kN/m3;av为土的压缩系数,kPa-1;e0为土体初始孔隙比。
一维固结基本方程[式(2)]的初始边界条件为
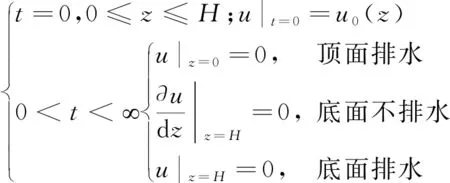
(4)
1.3 任意加载速率下软土地基的一维固结方程的通解
根据图2,现以上表面排水、下表面不排水为例,根据初始边界条件[式(4)],应用傅里叶级数法和分离变量法相结合[15]的方法求解软土地基在任意加载速率下的一维固结基本方程[式(2)]。可令孔隙水压力u(z,t)和加载速率f(t)为

(5)
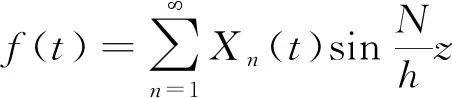
(6)
式中:h为最大排水深度,在单面排水条件下为土层厚度,双面排水条件为土层厚度的一半。
由式(6)可得
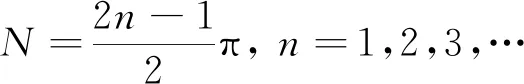
(7)
将式(5)和式(6)代入式(2)中可得

(8)
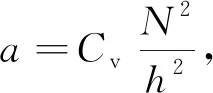
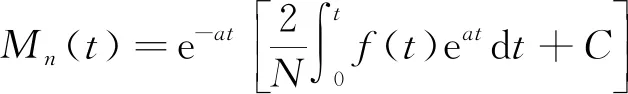
(9)
将式(9)代入式(5)并由初始条件[式(4)]第一式可得
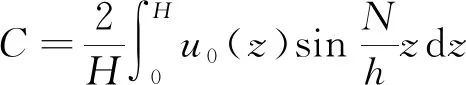
(10)
故可求得解为

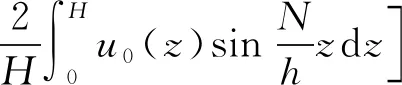
(11)
将式(11)代入式(5)得任意加载速率下的一维固结基本方程[式(2)]的通解为
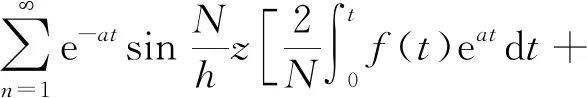
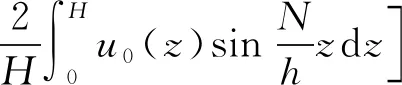
(12)
式(12)中:u0为初始孔压。
由有效应力原理以及固结度和沉降与有效应力的关系,可知固结度U(t)和沉降S(t)为
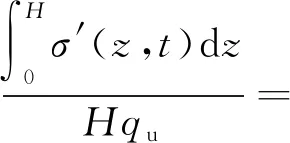
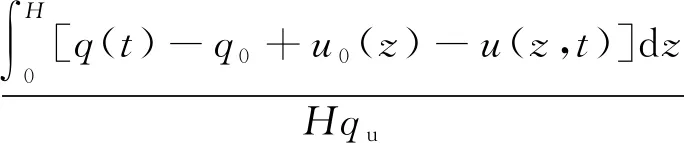
(13)
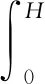
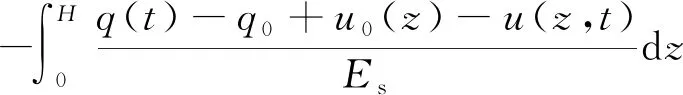
(14)
式中:q0为初始荷载;qu为荷载变化值qu=qn-q0。
2 线性加载作用下软土地基的一维固结解析解
施加的荷载q(t)是线性加载,随时间t的变化情况如图3所示,并得出荷载随时间变化方程式为
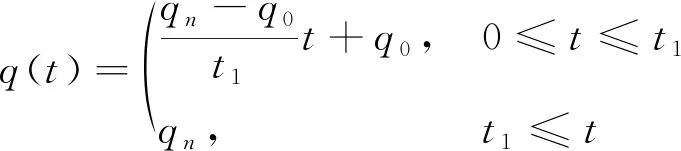
(15)
式(15)中:qn为加载后荷载;t1为加载时间。
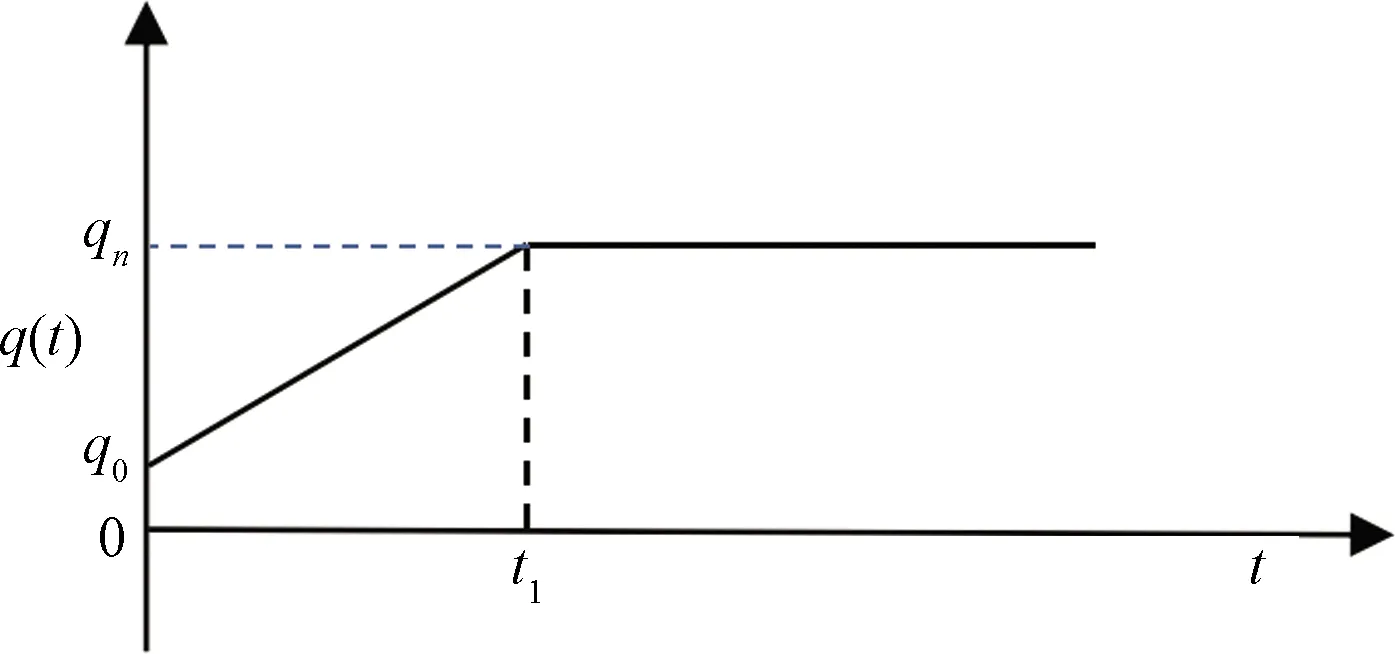
图3 荷载-时间变化曲线Fig.3 Load-time curve
各时间段的应力条件为
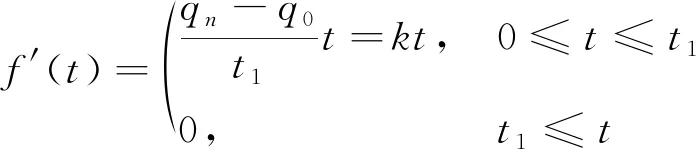
(16)
各时间阶段孔隙水压力的连续条件为
u1(t=t1)=u2(t=t1)
(17)
令初始孔隙水压力u1(z)=q0,将各阶段加载速度式(16)代入式(12),并由边界式(4)和式(17)可知线性加载下软土的一维固结表达式为
u(z,t)=
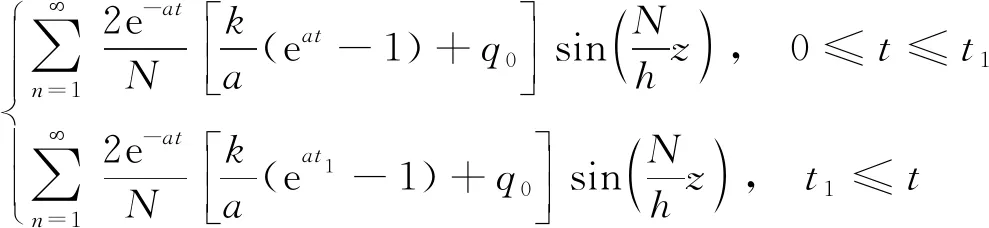
(18)
将式(18)分别代入式(13)和式(14)中,可得固结度和沉降的解析解为
U(t)=
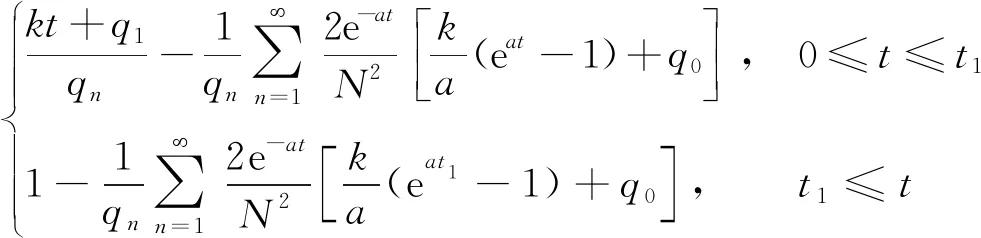
(19)
S(t)=
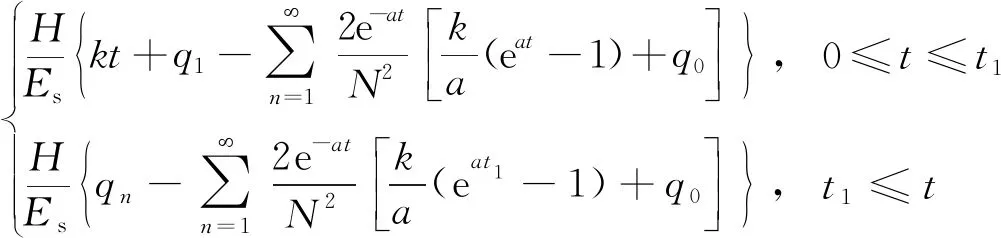
(20)
为了便于比较,将太沙基一维固结解解答列为
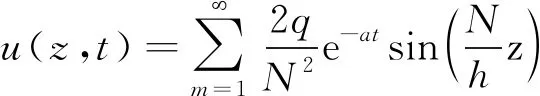
(21)
3 线性加载下理论结果分析
3.1 线性加载下超静孔压的变化规律
从线性加载下孔压的解析解式(18)中可以看出,加载引起的超静孔压受加载速率、加载量、固结系数及初始孔压共同影响。超静孔压k0定义为加载过程中某时刻孔压值与加载初期孔压值的差值。通过MATLAB对式(18)进行编程,其中假定q0=0,Cv=0.55 m2/d,加载量q=60 kPa,加载速率k=5 kPa/月,H=10 m,其余变量,取双面排水,并作太沙基一维固结理论下超静孔压进行对比,结果如图4所示。
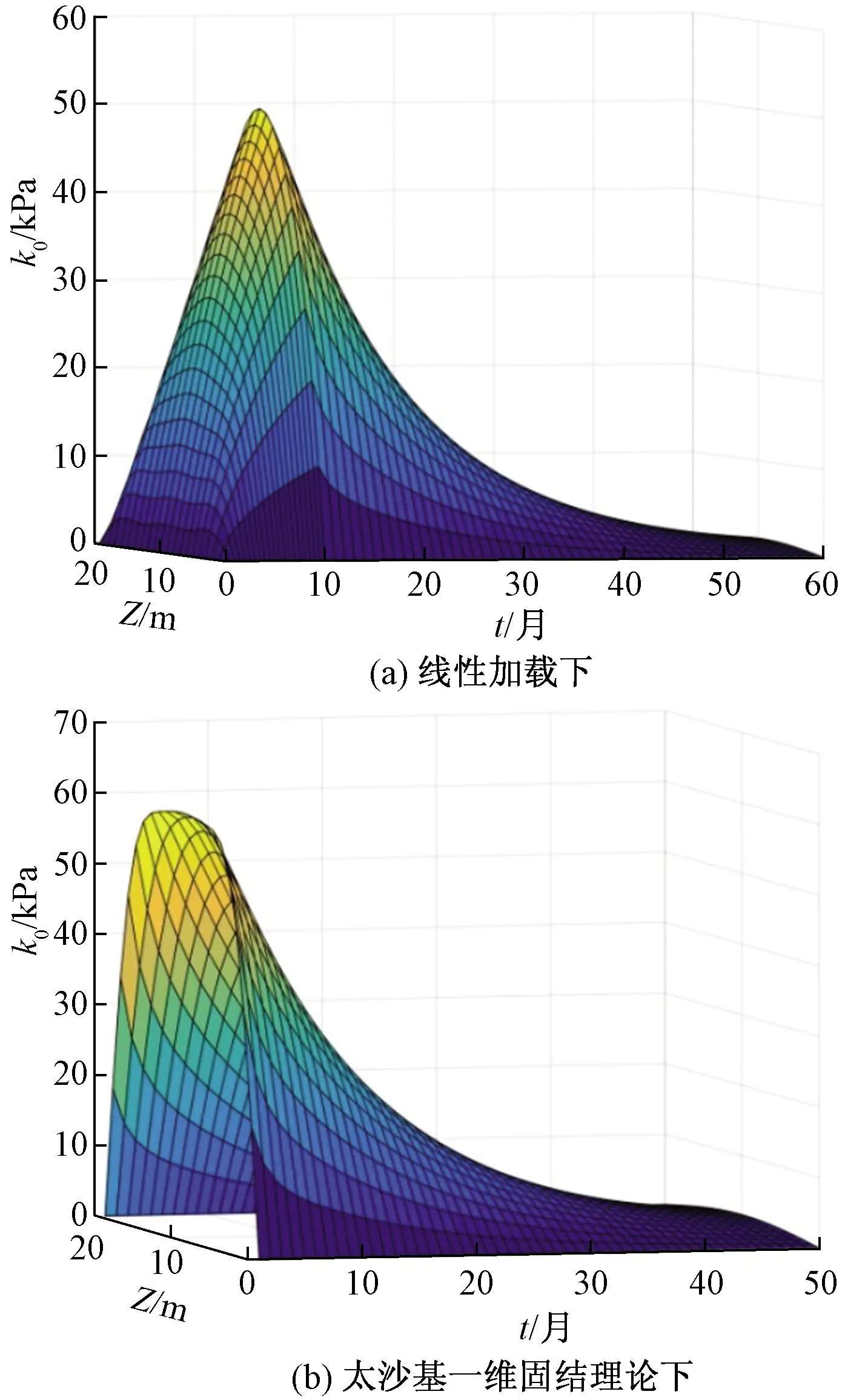
图4 超静孔压随时间和深度的变化Fig.4 Variation of excess pore pressure with time and depth
从图4可以看到,在相同的参数取值下,线性加载的最大超静孔压值明显小于太沙基解,这说明在加载过程中已有超静孔压在消散;线性加载下超静孔压值由零增长到最大值,此外还可以看到孔压的变化过程,而太沙基解直接突变到最大值;两者的最大超静孔压值和消散速率都在加载结束的时刻最大。结合现实分析,可以发现线性加载下孔压解比太沙基解更符合实际情况。
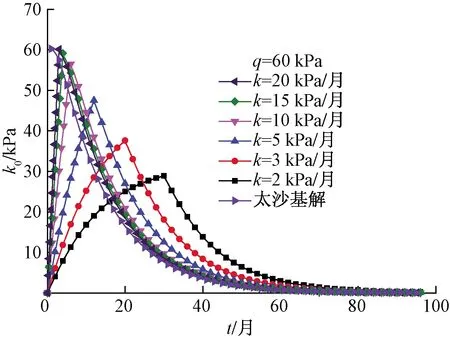
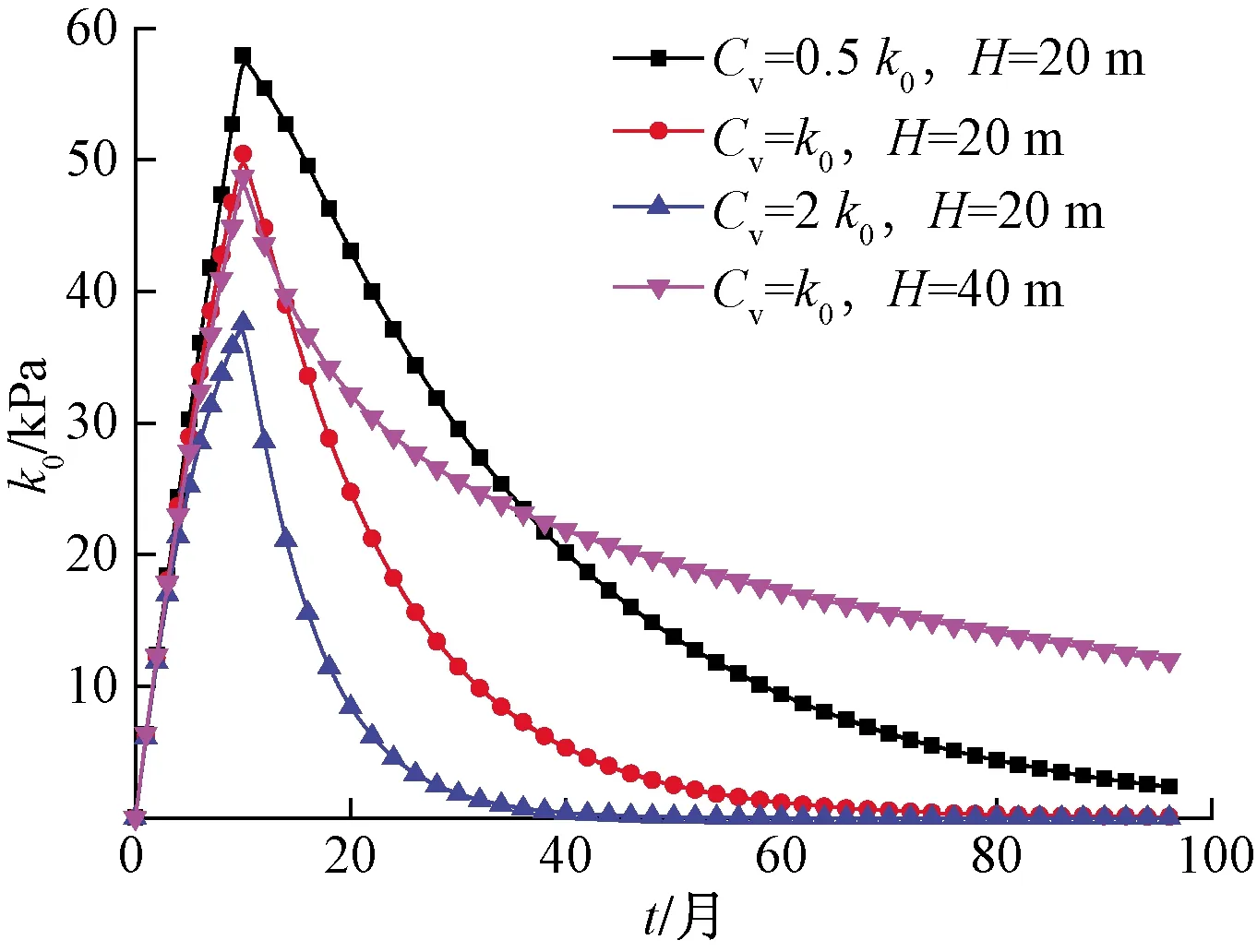
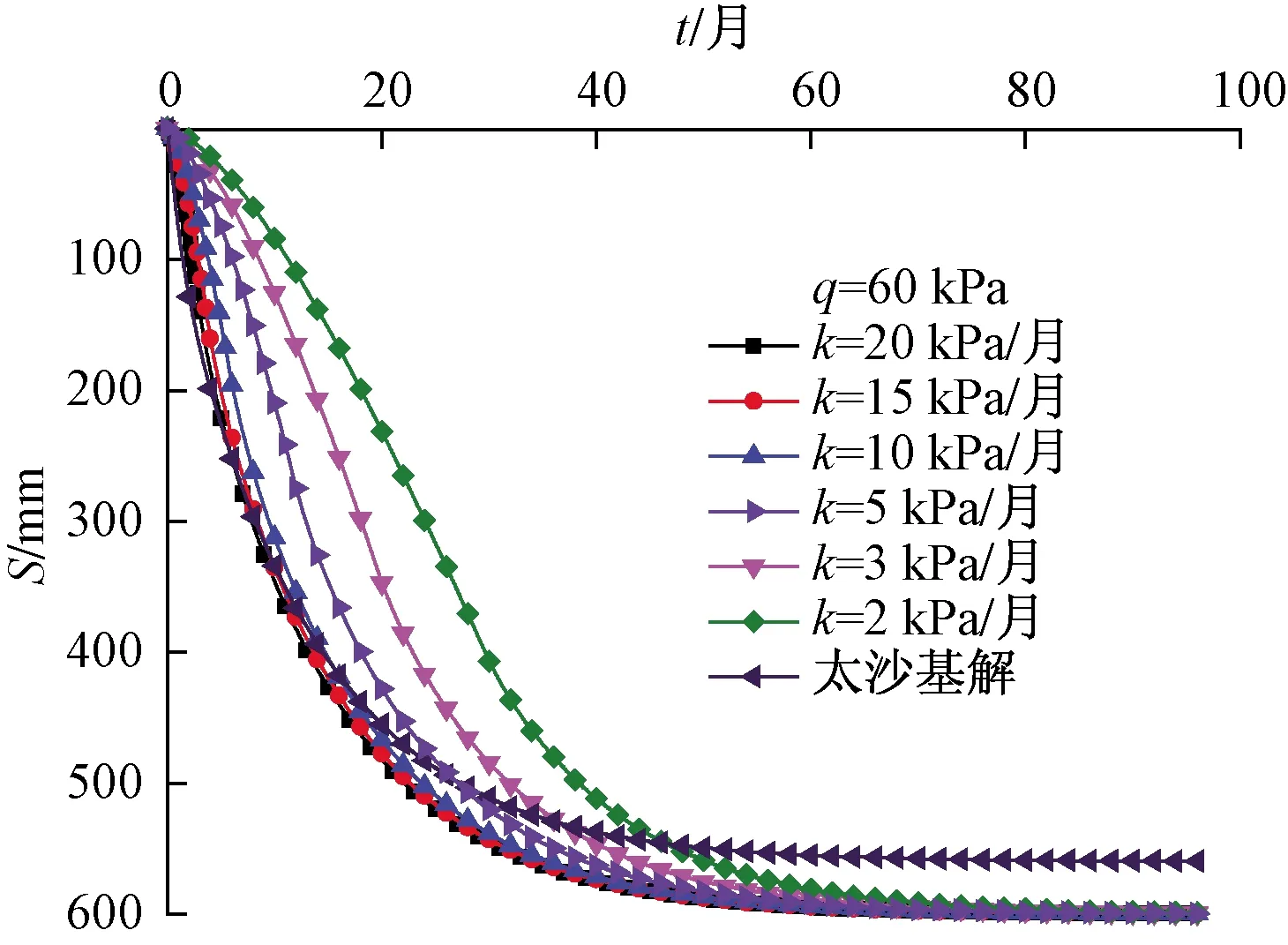
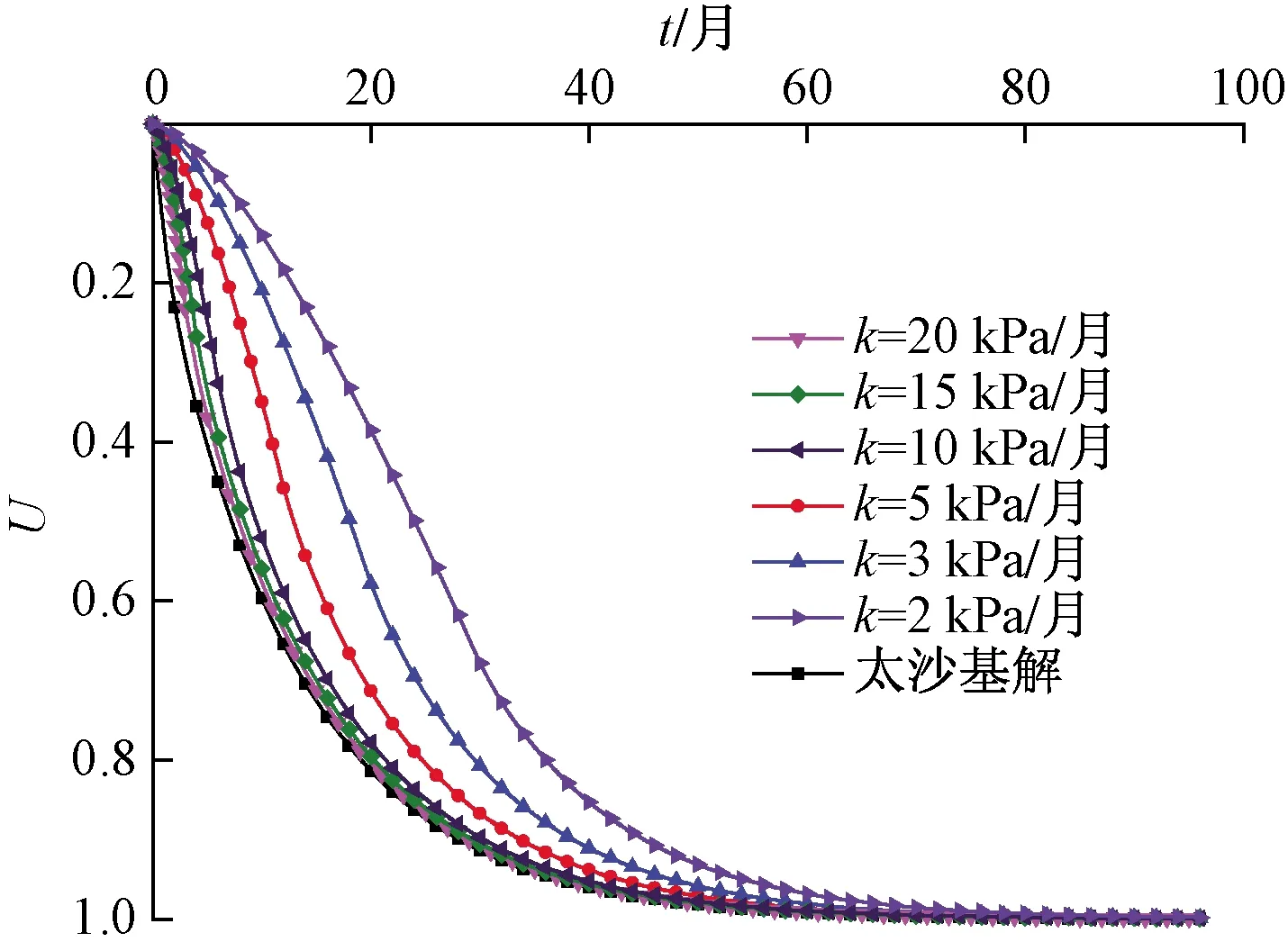
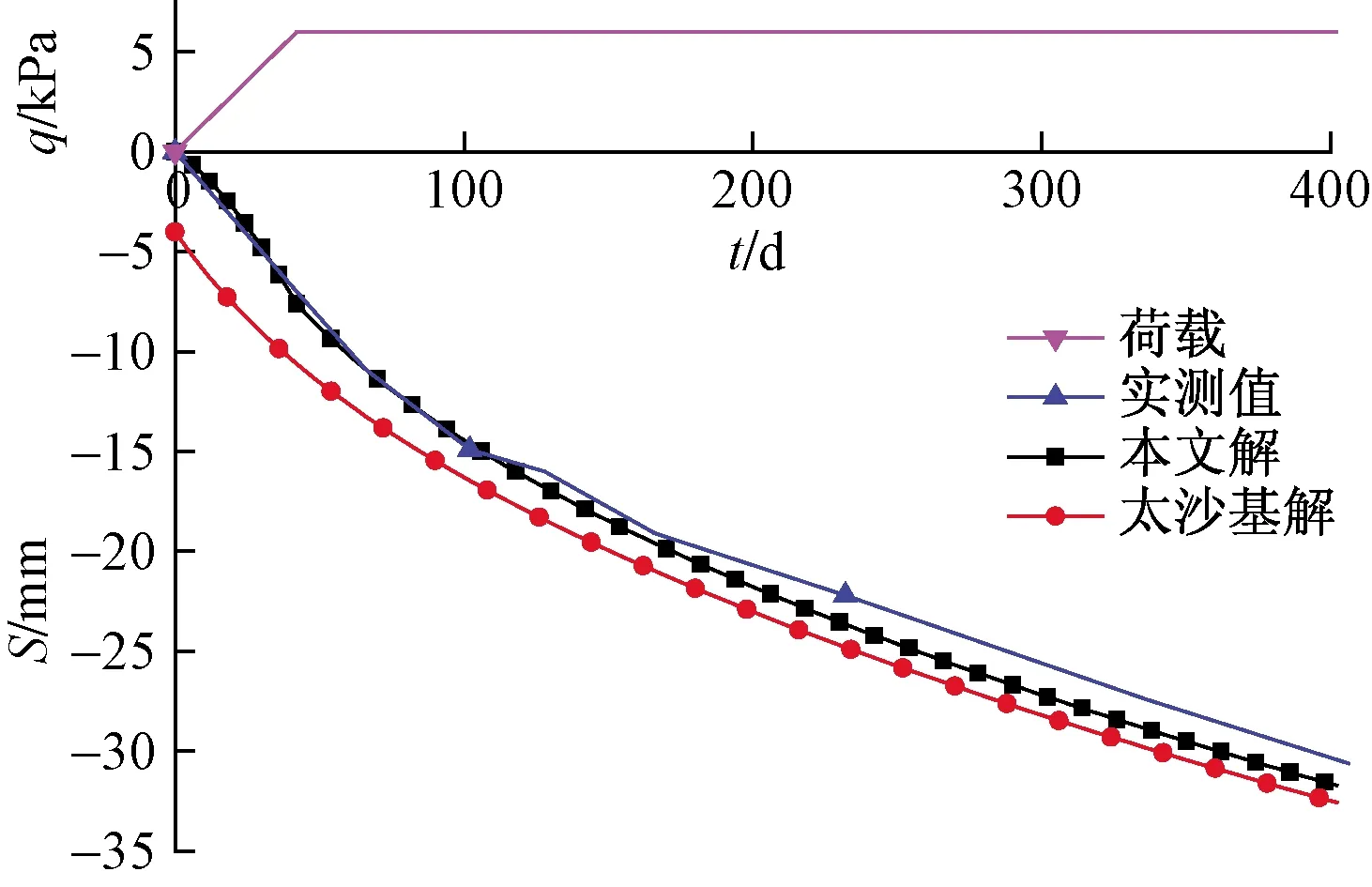
图5所示为不同加载量和加载速率引起的最大超静孔压变化,可以看出:当加载速率k<2 kPa/月时最大超静孔压值与卸荷量基本无关;在加载量一定时,加载速率k对最大超静孔压值的影响存在临界值k1和k2,当k 图6所示为不同的加载速率引起的超静孔压随时间的变化曲线,可以看出:超静孔压的消散速率随着加载速率的增大而增大;加载速率影响超静孔压的增长路径和最大超静孔压值;在线性加载作用下产生的超静孔压,其变化可以分成增长期、快速消散期和缓慢消散期三个阶段;加载速率越大,线性加载下的超静孔压与太沙基解越相似,即说明了本文固结解正确性,也验证了图5当加载速率大到临界值k2时,相当于瞬时加载。 图7所示为固结系数和排水距离对超静孔压的影响变化曲线,从图7可以看到:在加载速率一定时,固结系数不仅可以影响超静孔压值还影响超静孔压的消散时间,最大超静孔压和其消散时间随固结系数的增大而减小;通过对比分析可知,固结系数还影响着临界加载速率,临界加载速率k1和k2随着固结系数的增大而增大;超静孔压的消散时间同时还随着排水距离的增大而延长。所以在理论分析或者有限元软件模拟时采用准确固结系数和排水距离可以有效地提高结果准确性。 图5 不同加载量和加载速率引起的最大超静孔压Fig.5 Maximum excess pore pressure caused by different Loading amounts and loading rates 图6 不同的加载速率引起的超静孔压随时间的变化Fig.6 Variation of the excess pore pressure over time due to different loading rates 图7 固结系数和排水距离对超静孔压的影响Fig.7 Effect of consolidation coefficient and drainage distance on excess pore water pressure 图8是不同的加载速率下沉降随时间的变化曲线,可以看出:地基沉降的速度随着线性加载速率减小而变缓;加载速率改变沉降路径而不改变最大沉降值;随着加载速率减小加载阶段结束时刻地基产生的沉降越来越大,如加载速率为2 kPa/月时,地基在加载过程中产生的沉降近乎总沉降的一半,说明加载缓慢时,如果不考虑加载过程中产生的沉降,将导致非常大误差;加载速率越慢,与瞬时加载差异越大,太沙基解仅适用于大加载速率,对于加载速率较慢的实际工程并不适用。 图8 不同的加载速率下沉降随时间的变化Fig.8 Variation of settlement over time at different loading rates 图9是不同的加载速率下固结度随时间的变化曲线。可以看出:地基固结速率随着线性加载速率变小而变慢,由固结度的定义可知,固结度表示超静孔压的消散,即验证了图6超静孔压的消散速率与加载速率的关系;但随着加载速率减小,当加载阶段完成时,固结度增大;加载速率改变固结路径而不影响固结时间;当固结时间充分大时,固结度逐渐趋向于一致;线性加载速率越慢,与太沙基解固结路径差异越显著。 图9 不同的加载速率下固结度随时间的变化Fig.9 Variation of degree of consolidation with time under different loading rates 由文献[14]佛山—开平高速公路全长约80 km。该高速公路地处珠江三角洲平原,地质条件复杂。路基下土体多为流沙泥质软土和淤泥质土。其中K10+430通道为4.5 m×3.0 m,其地质条件为:0~2.5 m为亚黏土,2.5~6.6 m为淤泥质黏土, 6.6~14.4 m为细沙,通道顶部有0.7 m的填土荷载,填土分两次填,在第一次沉降稳定后填筑第二次,第二次填筑可简化为线性填筑加载过程,如图10所示。 图10 本文解、太沙基解和实测值对比Fig.10 Comparison of this solution, Taisha solution and measured values 从图10可以看到线性加载作用下的沉降曲线与实测曲线有较好的吻合性,尤其是在前期线性加载阶段,太沙基解由于不存在加载阶段,导致沉降存在突变,结合实际分析可知,线性加载下的固结解比太沙基解更符合现实,有更高的真实性,并且理论值与实测有相同的变化规律,说明式(20)可以用来预测地基在线性加载下某一时刻的沉降量以及求解的线性加载下固结方程解析解具有实际工程意义。 (1)通过太沙基一维固结理论,推导出任意加载速率下的一维固结方程的通解,并给出了线性加载下固结方程的解析解。 (2)在加载速率一定时,加载引起的最大超静孔压值与加载量近似成线性增长关系;在加载量一定时,加载速率对最大超静孔压值的影响存在临界值;加载速率影响超静孔压的增长路径和消散速率以及最大超静孔压。 (3)加载作用下软土地基产生的超静孔压可以分成增长期、快速消散期和缓慢消散期三个阶段, 固结系数影响临界加载速率;排水距离影响超静孔压的消散时间。 (4)加载速率改变沉降路径而不改变最大沉降值,加载速率越慢,与瞬时加载差异越大;固结速率随着线性加载速率变小而变慢;加载速率改变固结路径并且影响固结时间;当固结时间充分大时固结度逐渐趋向于一致。 (5)通过工程实例对软土地基加载下沉降值及其规律进行对比分析,发现基于线性加载固结方程的解析解得到沉降理论值及变化规律与实测值有较好的吻合性,证明求解的固结方程的解析解具有较高的可靠性,对软土地基在线性加载下施工设计具有一定的理论指导作用。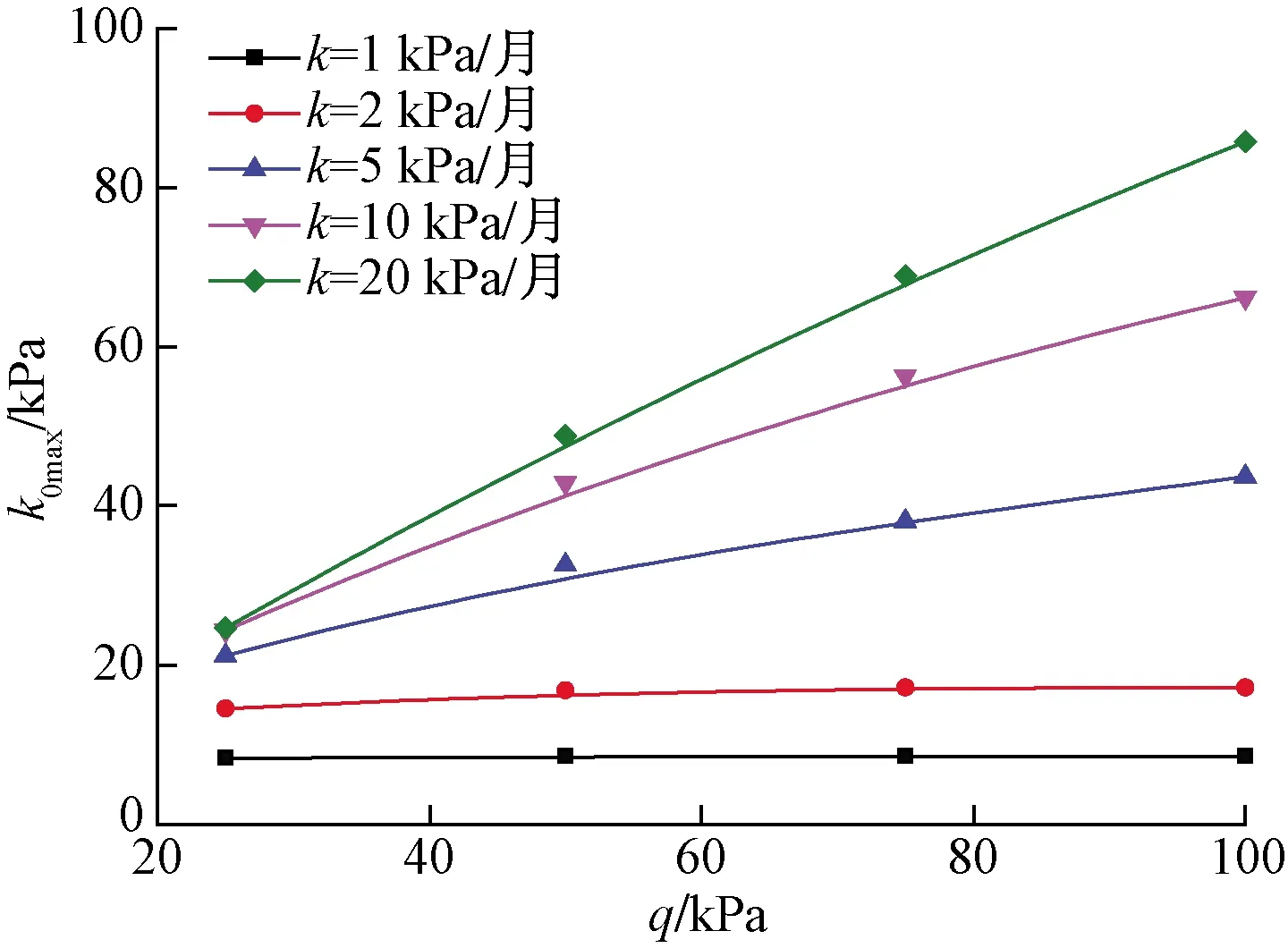
3.2 线性加载下地基沉降和固结度变化规律
4 实例分析
5 结论
