基于MPGA的电动汽车充电站选址规划

倪超 王菲 仇经纬 丁俊 许飙

（国网江苏扬州供电公司 江苏省扬州市 225000）

随着新能源汽车和充电基础设施产业的迅猛发展，电动汽车充电业务已积累大量用户，根据有关部门统计数据显示，截至 2020年初，我国新能源汽车保有量达418 万辆，其中纯电车保有量达350 万辆，占新能源汽车总量的83.7%[1]。市场上的纯电车会面临充电问题，而零散的充电站无法最大效率的发挥其使用效率，因此，需要对充电桩的合理选址布局，满足用户需求的同时最大程度上提高经济效益[2]。

文献[3]对充电桩用户行为的特性进行分析，得到充电站接受充电桩服从正态分布的结论。文献[4]研究了电动汽车充电站的选址研究，并提出充电站的建设原则。文献[5]以最小配电网损耗和节点电压为约束条件进行选址优化，文献[6]利建立了电动充电桩的最优规划数学模型，并得到了仿真验证。但是以上这些都没有考虑运营商收益最大化以及用户的用电需求的有效结合，文献[7]利用多种群遗传算法对包含分布式电源的配电网故障区段进行定位，并通过实际算例证明了该故障算法的可行性。但是以上的算法都没有将经济效益作为重要考虑因素，同时也未从多维度的考虑电动汽车充电站建设的约束条件，因此，本文展开对变电站玄龟进行规划分析。首先进行了电动汽车充电站的净收益分析，并以经济最大化为目标，同时以交通车流量密度、用户充电需求、电网电能质量经济性为约束条件建立规划模型，然后通过多种群遗传算法实现对电动汽车充电站的规划选址求解，最后经过江苏某地区算例进行充电站的规划求解，结果表明该地区规划6 个充电站为宜，证明本文提出算法的可行性。

1 充电桩成本效益分析及优化模型

在电动汽车充电桩市场,其运营服务商可以来自于国网公司或者是新能源运营商。国网公司作为服务商时直接将电能售给用户，同时进行充电桩的设备维护、反馈用户的需求响应，并达到盈利的目的。新能源运营商将电网的电能出售给用户，从而实现盈利的目的，如图1所示。因此，充电站的选址规划必须满足运营商或者电网公司的盈利目的，同时也要考虑用户的利益。

接下来对电动汽车充电站的净收益进行分析，本文考虑以充电站运营商或者电网获得的净收益最大为规划目标进行充电站选址计算，运营商或电网所获得的净收益为Vnp 表示，其计算公式如下：

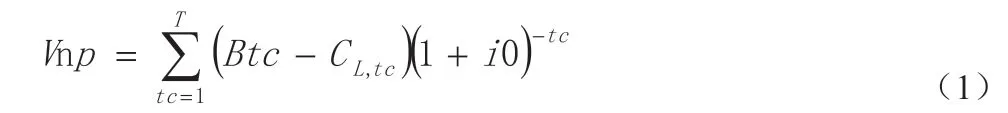
其中T 表示充电站运行周期（单位是年），tc 表示充电站运行到第tc年，Btc 为充电桩在运行周期内的资金收益，CL,tc 表示充电桩在运行周期内的即成本，i0 为资金折现率。上式就是充电桩的成本净收益计算公式。

本文以充电站运营商获电网获得的最大净收益值为规划目标，以交通车流量密度、用户充电需求、电网电能质量经济性为约束条件建立数学模型，如式（2）所示。

交通车流量密度是建设充电桩的主要考虑因素之一，只有适当的充电桩才能既满足用户的需求，汽车流量大的地区未来流量也会提高，因此需要在车流量大的地方建设充电桩，即未来的市场更有前景的同时，经济效益也会越来越高。其约束条件为：每个充电桩的车流量密度都要大于每个充电桩所能容纳的车流量密度的最小值，区域内所建设的充电桩数量要小于等于规划建设的最大充电桩数量。

图1：三电网-运营商-用户关系

Step1

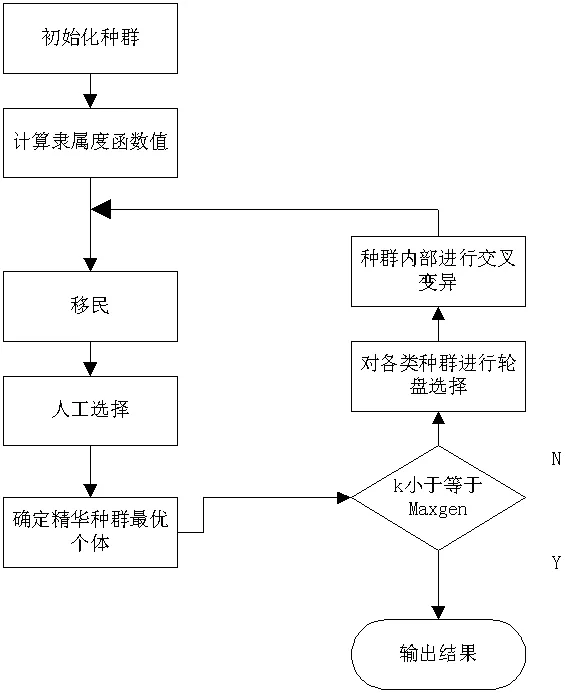
图2：多种群遗传算法流程图

电网电能质量经济性也是建设充电桩的主要考虑因素之一，充电桩的直流和交流负荷会对电网运行的波动性产生危害，因此需要考虑其对电网运行的影响，保证充电桩接入后电网的各项指标运行正常。其约束条件为：电力系统的节点电压值在节点电压幅值上下限之间，同时充电桩的电流要小于等于其正常运行的最大电流。

建设充电桩还需要考虑的因素是满足用户的需求。其约束条件为：充电桩所能提供的负荷要大于等于该地区电动汽车充电负荷，同时每个充电桩的服务半径要小于等于充电桩的最大服务半径。

2 多种群遗传算法求解充电桩选址规划

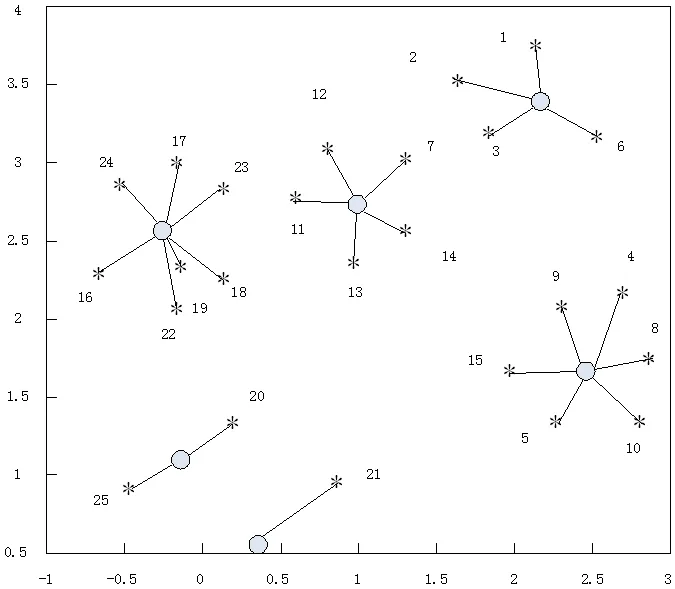
图3：充电桩选址优化结果

本文提出的充电桩选址规划模型是一个非线性的优化问题，通常采用智能算法进行求解。本文采用多种群遗传算法求解此模型，多种群遗传算法是达尔文自然最优选择的生物进化计算模型，该算法是将问题以二进制的形式编码成基因，个体是由若干个基因组成，种群是又多个个体组成的，先给定初值初始化种群，然后重复进行种群内部以及种群间选择、交叉、变异以及移民等操作，使得种群进行进化，进而求得最终结果[7]。传统遗传算法容易陷入局部区域，导致求解为局部最优解非全局最优解，而多种群遗传算法能够快速准确进行全局搜索，然后得到最优解，MPGA 的基本的操作如下：

（1）选择。从目前的种群个体中选择出最优秀的个体，然后根据目标收益的最大值对种群的大小进行排律，目标收益大的被选择进行下一代，这一原则体现了优胜劣汰，只能在一个固定的种群进行选择。

（2）交叉。将上一代的染色体进行重组可以得到新的个体，对种群内部的个体进行随机组合，以一个的概率（Pc）交换产生新的基因，充分表示信息交换的目的。

（3）变异。个体基因的染色体中存在一部分的基因以某一概率进行基因突变，从而产生新的个体，这样就解除了目标值只能由初始种群决定的限制。

（4）移民。将个体内最优秀的个体进行移民，遗传到下一个种群当中去，并进行计算目标收益的最大值，同时按照上述操作进行排序，同时选出最优秀的个体继续遗传，直到目标收益净现值最大为止，此时，目标函数即为全局最优规划目标。多种群遗传算法能够解决陷入局部最优解的缺陷，还能进行多种群的选择，交叉，变异，移民等操作，但是由于算法的数据比较大，要适当选择种群的个数以及迭代的次数，这样才能既满足规划的要求，同时也能节省计算机的优化时间。

其具体的算法流程图如图2所示。

3 实例分析

2020年，江苏某区域的面积为14.9km2，人口密度为13000 人每平方米，人均汽车量30%，其中电动车占比30%，各个小区的电动汽车位置及数量数据见文献[8]。其中假设用户有两种充电模式选择，一种是快充，一种是普通充电用户。选择快速充电的用户占所有用户的85%，充电时间T=1.5，充电功率P=150kW，选择正常充电的用户比例为15%，充电时间T=5，充电功率P=20kW，所有车辆每两天充电一次。规划区域内的变电站计算公式如式（3）。

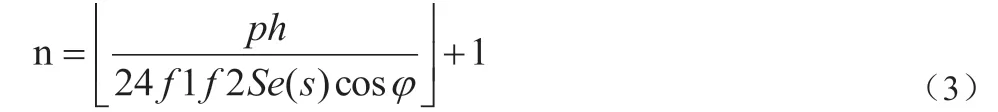
其中：h 为规划区内电动汽车总数，[]内取整数，计算得到m=6。

利用m=6 进行优化，得到充电桩选址优化结果如图3所示。

图3 中“*”号代表小区，所处的位置表示空间位置，经过计算优化之后，六个“o”代表电动汽车充电站的位置。由图可知，1 号充电桩覆盖的区域是1,2,3,6 号小区，2 号充电站覆盖的区域16,17,18,19,20,22,23,24 号小区，3 号充电桩覆盖的区域是20,25 号小区，4 号充电桩覆盖的区域是21 号小区，5 号充电桩覆盖的区域是4,5,8,9,10,15 号小区，6 号充电桩覆盖的区域是7,11,12,13,14 号小区。目标函数的Vnp 的最大值为2.63×107元/年。

4 结论

针对电动汽车找不到充电站及部分建设的充电设备利用率不高的问题，本文对充电桩的选址进行优化。首先对分析充电桩的成本效益进行分析，并确定优化模型，同时考虑三个影响建设充电桩的主要约束因素。然后采用多种群遗传算法对充电桩的选址模型进行优化，最后结合实例进行验证，结果表明天津某地区适合建设的充电桩的数量为6，同时得到其经济效益的最大值为2.63×107元/年，进一步证明本文选址优化算法的可行性，对城市充电桩的选址具有一定的指导性意义。