基于多区域RANSAC的地面点云提取算法

管郡智 潘卫清

（1.浙江科技学院机械与能源工程学院 浙江省杭州市 310000 2.浙江科技学院理学院 浙江省杭州市 310000）

1 前言

随着科技的发展，高精地图在无人车应用越来越广泛，也是无人车普及的关键一步[2]。而激光雷达又是高精地图的重要的传感器，点云算法的研究也成为感知技术的重要的一环。现在的大多数无人车都是在水平的地面上行驶，因此，在平面上检测障碍物、测定相机相对于地面的姿态等等都成为非常有用的技术。目前已经发展出几种地面点云的提取方法，文献[3-4]提出最小二乘法、特征值法等从三维点云中拟合地面，其原理是基于给定的目标方程，最大程度地估算和优化模型参数以给定的点云数据。由于最小二乘法和特征值法算法本身的局限性，并不能有效地抵制异常数据的干扰。这种情况下，文献[5-7]提出先用随机样本一致性（random sample consensus, RANSAC）算法剔除大量的异常数据，再用最小二乘法拟合平面。虽然取得一定的效果，但是应用于KITTI 数据集上，其地面点云提取的稳定性依然没有有效解决。本文提出在将点云数据分割为多区域的情况下，结合RANSAC 和最小二乘法提取地面点云，并用KITTI 的点云数据进行验证，实验表明本文的方法可以有效提高地面点云提取的稳定性。

2 基于多区域RANSAC地面点云提取算法

2.1 点云数据栅格化处理

将点云数据看作是一个整块，用最小的长方体将其包围，然后根据点云的实际尺寸分别设定长方体的最小边长，再将长方体划分为三维的网格，即将点云进行栅格化，形成点云数据的多区域分割[8]。

（1）计算点集合{P1,P2,…,PN}(其中Pi=[xi,yi,zi]T,i=1,2,…,N) XYZ三个坐标轴的最大值和最小值：

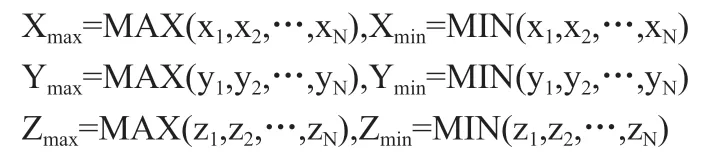
（2）确定栅格化边长。栅格化的边长R 确定了每个网格里面点的个数以及计算效率。栅格化边长R 越小，网格数量越多，占用的计算机资源越多，运行速度越低，效率低下。栅格化边长R 越大，那地面点云的拟合稳定性就越低，就失去栅格化的作用。所以，会根据实验的效果来确定栅格化的边长R。确定了栅格化边长之后，就可以计算点云网格的维度：

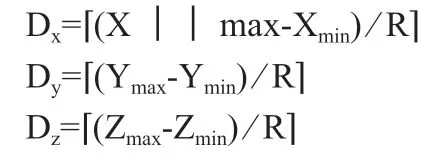
（3）计算栅格化之后每个点的索引。对栅格化之后的点云进行编码，确定每个点所在的网格的编号。每个点在网格中的索引h：

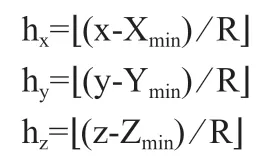
表1：不同算法提取地面点云数量比较

2.2 RANSAC算法

随机样本一致性( random sample consensus, RANSAC)是一种用迭代的方式拟合出数学模型参数的算法，该算法的优点是对包含异常值的数据有较好的鲁棒性[9-11]。将RANSAC 算法应用到地面点云的提取中，除地面点云外，都属于异常值点云数据，具体实现步骤：

（1）在点云中随机选取三个点并向量的叉乘计算三个点所在平面的法向量：

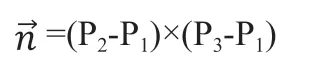
其中，P1=(x1,y1,z1), P2=(x2,y2,z2),P3=(x3,y3,z3)。

（2）计算点云中任意一点到这个平面的距离：

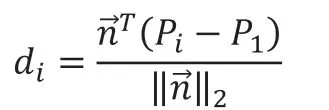
其中，Pi为点云中任意一点，i=4,5,…,N。

（3）设定阈值di<τ 以提取出正常的点云数据，将符合条件的点云保存下来，并记录点的数量。

（4）重复步骤 1) ～ 3) T 次，然后将点数量最多的点云保存下来，再用最小二乘法微调地面点云以拟合出准确的平面参数。

在RANSAC 算法中，超参数τ 和 T 的设定也非常重要。迭代次数T 对模型的影响很大，T 设置过大，会增加运行时间，影响运行速度，而运行过小也会导致拟合不出的平面，不过可以从理论推导的角度选择合适迭代次数T：

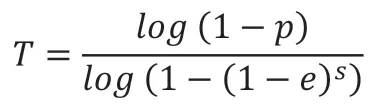
其中，e：点云数据中异常点的比率；

s：每次迭代选取点的数量；

T：RANSAC 最大迭代次数；

p：至少一次选取到正常点的概率。

而τ 选小了则会漏掉地面点云，选大了会将异常点云当作地面点云，本文以实验可视化来确定阈值τ 的大小。这里使用所有点到平面距离的标准差σ 作为阈值：

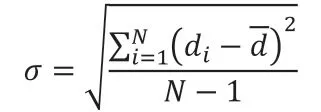
取τ=2σ, 当 di>τ=2σ 时，此点被认为是异常值点，不当作地面点云提取；反之，为有效值点，被当作地面点云提取出来。

图1

2.3 最小二乘法

经过RANSAC 初步拟合出地面之后，再用最小二乘法进行微调。由于 RANSAC 拟合带有随机性，且当异常值点云的比率e 设置不正确的情况时，即使在最大迭代次数之内，也没有提取到准确的地面点云。那就没有必要执行N 次迭代，设定一个期望正常值比率E：

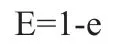
当RANSAC 提取的地面点云比上点云总数大于E 时，就终止迭代，然后再将提取到的点云用最小二乘再一次拟合，计算得出的地面模型参数：

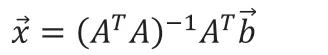
A 为RANSAC 提取的点云组成的矩阵, A=[P1…PS]T且 S

最后，根据拟合出来的平面模型参数，在每个网格点云中提取出地面点云。

2.4 地面点云提取流程

（1）对原始点云进行栅格化处理，并且对每一个网格进行编码；

（2）对网格里的点云做随机样本一致性，达到期望正常值比率E 就停止RANSAC 迭代；

（3）根据（2）步得到的点云，用最小二乘法重新拟合出地面模型的参数，根据参数提取网格中的地面点云；

（4）遍历所有网格，重复第（2）步和第（3）步的操作，直到所有网格都提取到地面点云。

3 实验分析及结果

3.1 实验数据

实验用到的数据选自KITTI 的点云数据集，使用python 对所有算法进行仿真，点云数据不做任何预处理，用原始数据来验证本文提出的算法的稳定性。

3.2 算法比较

本次实验挑选的KITTI 某一个点云数据来比较算法提取地面点云的数量以及可视化，其中栅格化的尺寸是20 米。由表1 可以看出,提取地面点书最多的是本文提出的算法，从图1(a)也可以看出，本文算法能够很稳定地将地面点云提取出来，同时RANSAC 和最小二乘法的结合也比纯粹的RANSAC 算法效果好很多。

4 结语

传统的算法，如随机样本一种性算法和最小二乘法都不能从点云数据中稳定地提取地面，而地面点云的提取又是众多工程应用的重要环节之一。本文提出了在多区域的情况下，结合随机样本一致性算法和最小二乘法来提取激光雷达扫描到的地面点云，从实验可以看出算法的稳定性。