智能上肢康复机器人的设计
2020-02-02郭迎九郭澜黎恩铭
郭迎九 郭澜 黎恩铭
(1.北京城市学院信息学部 北京市 101309 2.北京大学医学部 北京市 100083)
目前,脑卒中和中风发病率逐年上升[1][2],这种疾病引发了患者肢体运动功能的丧失尤其是上肢运动功能的丧失,极大地影响了患者日常的生活。因此脑卒中和中风患者的治疗和康复显得异常迫切和重要。临床康复中,康复医师通常以对患肢进行一对一的连续被动训练,劳动强度大,训练效果不能保证,而现有的康复机器人和辅助器械智能化水平不高,因此,开发智能化水平高的康复机器人具备很高的应用价值,是当今国内外研究的热点领域。
1 国内外现状分析
国内外在这方面也作了不少研究工作[3]。国内哈尔滨工业大学等研制了基于SEMG 信号的外骨骼上肢康复机器人[4],国外美国、日本等也研制了相应的上肢康复设备,如2010年日本Akita Prefectural 大学的Koi-chi Kirihara 等人开发了气动式连杆上肢康复支撑设备[5]等。
现有的康复机器人可以帮助患者进行康复治疗,治疗效果较传统方法有明显的提高,但机器人的智能化水平不高,需要开发具备一定智能化水平的康复机器人。
2 智能康复机器人结构设计及仿真
2.1 机器人结构设计
我们设计的智能康复机器人结构如图1所示。根据人体解剖学理论,从康复运动的实际出发,选择了上肢最基本也是最重要的3个自由度:肩部屈/伸、肘部屈/伸和腕部屈/伸。图1 中从下到上的三个黑色圆点分标对应肩关节、肘关节和腕关节,它们皆为回转关节,由伺服电机通过减速器带动转动,杆件1、2、3 分别代表臂、前臂和手。3 个关节协调运动,带动臂、前臂和手实现竖直面的预定轨迹运动。通过调节机器人的姿态和患者手臂的放置方式,可以实现上肢肌肉的康复训练(如表1所示意)。
2.2 运动学分析及仿真
2.2.1 运动学分析
机械手臂可以认为是由一系列关节连接起来的连杆机构所构成,各关节的几何关系可通过Denavit-Hartenberg(D-H)参数表来描述(见表2)。D-H 参数参数由杆件长度a、移动关节线位移d、杆件扭角α 和转动关节角位移θ4 个分量组成,以描述某一杆件相对于前一杆件的位姿。
机器人坐标系如图。根据坐标变换的原理,得:

表1:机器人自由度及相关运动肌肉群

表2:康复机器人D-H 参数表
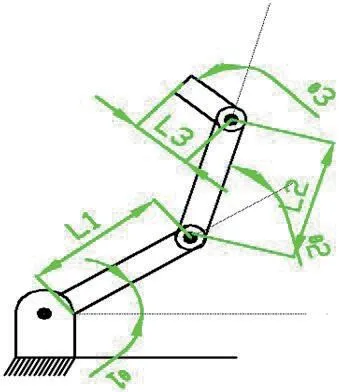
图1:康复机器人结构简图

图2:仿真三维图

图3:Matlab 仿真得到的曲线

图4:智能控制原理图

图5:康复机器人BP 神经网络结构图
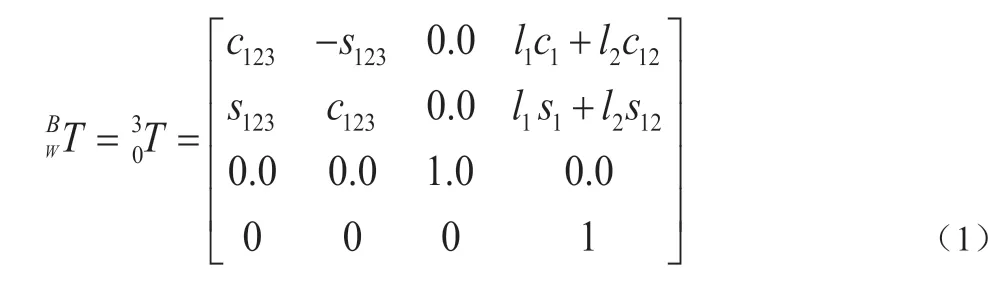
其中,c123=cos(θ1+θ2+θ3),s123=sin(θ1+θ2+θ3),c12=cos(θ1+θ2),s12=sin(θ1+θ2),c1=cos(θ1),s1=sin(θ1)。根据上述变换矩阵,可求得手部基点位置坐标为:

接下来对(1)的变换矩阵进行逆变换可以在确定末端坐标x,y和φ (φ 是连杆在平面内的方位角)的情况下,求解各个臂夹角。求解结果如下:

应用反切公式计算θ2:

令:

得:

由:

解出θ3。。接下来我们用Matlab Robotics 仿真软件对我们的结果进行验证。
2.2.2 运动学仿真
我们利用Matlab Robotics 软件进行仿真的杆件初始化代码如下:
L1 = Link('alpha',0,'a',0.25,'d',0);
L2 = Link('alpha',0,'a',0.25,'d',0);
L3 = Link('alpha',0,'a',0.125,'d',0);
L4 = Link('alpha',0,'a',0,'d',0);
L5 = Link('alpha',0,'a',0,'d',0);
L6 = Link('alpha',0,'a',0,'d',0);
代码中,alpha,a,d 为默认参数,由于我们只仿真机器人运动轨迹这些参数可以忽略不计,三连杆的长度分别为0.25 单位,0.25单位和0.125 单位。
连杆构建代码:
Bot=SerialLink([L1 L2 L3 L4 L5 L6]);
终止条件:
qr=[pi/4,pi/4,pi/4,0,0,0];
采样周期(时间2 秒,采样周期50 毫秒):
t=[0:0.05:2];
变换矩阵:
forward_kinematics = fkine(bot,qr);
模拟过程:
bot.ikine(forward_kinematics)
仿真三维模型如图2所示意。仿真时间2 秒、采样周期是50ms,记录末端点在基坐标系各坐标轴上的坐标值,得到机器人末端点的位移变化、速度变化和加速度变化,如图3所示。
图中,横坐标为时间(2s),综坐标为位移(米),速度(米/秒),加速度(米/秒2)。臂、前臂、手的长度分别是0.250米,0.250 米,0.125米。仿真与运动学分析一致,为康复机器人的设计提供了很好的验证工具。通过调整臂、前臂、手三个杆件的末端运动速度、杆件运动夹角θ 等物理量的变化调整康复机器人的运动强度。
3 机器人智能化控制设计
我们设计的智能化控制机器人利用AD8232 传感器测量心率并根据病人心率负荷要求实时调整康复机器人的运动强度,从而达到保证康复人员安全的目标。STM32 单片机主要采用PWM 方法控制各个伺服电机的转速和转角,控制依据是BP 神经网络通过机器学习得到的适合康复人员安全的运动强度目标。整个系统为一带负反馈的智能控制系统(图4)。康复运动的心率要求为:

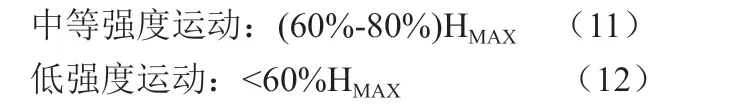

图6:BP 学习结果

图7:智能康复机器人样机
控制采用的BP 网络(Back-ProPagation Network)[6]是一种反向传播神经网络,通过样本数据的训练,不断修正网络权值和阈值使误差函数沿负梯度方向下降,逼近期望输出。它是一种应用较为广泛的神经网络模型,多用于函数逼近、模型识别分类、数据压缩和时间序列预测等。BP 网络由输入层、隐层和输出层组成,隐层可以有一层或多层。
我们设计的BP 神经网络采用三层,分别为输入层,隐含层和输出层,如图5所示意。输入层的输入数据分别为:臂、前臂、手运动速度以及臂、前臂、手运动的角度幅度即最大夹角常θ。模型选择正切函数tansig 作为隐层神经元的激励函数。隐层神经元数初设为4。
在康复病人实用机器人之前,我们需要对病人进行训练,采集数据集作为神经网络的学习数据集,采集的数据集包括臂、前臂、手运动速度以及臂、前臂、手运动的角度幅度即最大夹角常θ 和心率的关系。学习数据集完成后,BP 神经网络就可以进行预测。我们选定的仿真工具为Matlab Neural Network 工具包。仿真预测设定网络迭代次数epochs 为5000 次,期望误差goal 为0.00000001。在实际训练过程中,由于病人的身体原因,我们选定一康复病人的16个样本集P 目标集T 如下所示进行预测学习。经过173 次学习达到期望误差,仿真结果收敛。智能机器人在正常工作时可以依据病人的心率要求按照预测模型调整按机器人运动参数进行康复训练,保证训练的安全。
P=[0.10 0.20 0.15 0.18 0.20 0.22 0.10 0.15 0.18 0.20 0.22 0.10 0.15 0.18 0.20 0.22;
0.10 0.18 0.15 0.18 0.20 0.22 0.10 0.15 0.18 0.20 0.22 0.10 0.15 0.18 0.20 0.22;
0.10 0.20 0.15 0.18 0.20 0.22 0.10 0.15 0.18 0.20 0.22 0.10 0.15 0.18 0.20 0.22;
0.785 0.90 0.785 0.785 0.785 0.785 1.04 1.04 1.04 1.04 1.04 1.57 1.57 1.57 1.57 1.57;
0.785 1.54 0.785 0.785 0.785 0.785 1.04 1.04 1.04 1.04 1.04 1.57 1.57 1.57 1.57 1.57;
0.785 1.60 0.785 0.785 0.785 0.785 1.04 1.04 1.04 1.04 1.04 1.57 1.57 1.57 1.57 1.57;];
T=[80 100 85 88 95 100 83 87 89 99 106 103 107 120 130 136];
如图6所示,仿真学习结果说明了我们的预测方法是合理和可行的。预测模型可以作为控制康复机器人运动的指导模型,由AD8232 传感器结合STM32 PWM 控制器根据心率运动公式给予病人最适合的运动参数。
4 展望
智能康复机器人是医疗机器人的一个重要分支,是康复机器人的未来发展方向。本文设计的智能康复机器人机械结构采用铝制部件,生产成本低,重量轻。采用AD8232 传感器测量心率,通过STM32 单片机依据BP 神经网络算法智能化控制机器人,保证康复人员的安全。文章应用Matlab 软件进行了仿真。理论分析、仿真和样机实验证实了该智能康复机器人设计的可行性,如图7所示意。今后要继续对智能控制算法进行研究。
