利用微重力技术进行采空区探查可行性分析

刘净余

(五矿矿业控股有限公司，安徽 合肥 230000)

0 引言

在矿产开发过程中，地下大规模开采产生的矿区采空区会导致地下介质密度发生变化[1,2]。在重力勘探中，由于地下岩石、矿物密度分布不均匀或地质体与围岩密度具有较大差异能够引起地表观测到的重力值变化，这种变化被称为重力异常。矿产开发过程中的地下介质质量亏损，会影响地表重力值重新分布，采空区前后重力变化量能为微伽级，对于采集、处理的要求均较高。因此长期以来，煤矿地下采空导致的地表重力异常效应因量级较小而被忽视。

近年来微重力测量技术得到发展，伴随着当代高精度重力仪的出现和测量方式的改进(高程、测点测量等)，重力测量的精度得到了极大的提升。传统重力测量是毫伽级别，微重力测量的精度是微伽级别。微重力测量精度的提高，使得重力勘探分辨率极大地提高了微重力探测技术在油气田开发监测、资源勘探、土木工程技术等诸多领域获得应用[3,4]。

对于大部分矿区，多年来的大规模高强度开采已经形成了大量的地下采空区，这些采空区分布较为复杂，探测难度大；采空区探测方法中的物探技术，如浅层地震法、探地雷达法和可控源音频大地电磁测深法是较为有效的手段，其中微重力技术能够有效反应地下介质密度分布变化，是重要的探测手段之一[5]。地下大规模矿产开采过程中产生的采空区会导致地下介质密度发生变化，能够反映介质密度变化的地面微重力技术，是实现采空区探查的有利手段，对矿产安全生产和地面保护具有实际意义。

建立采空区模型，利用正演数值计算，得到地表重力变化情况；讨论地下大规模采空区引起的重力场发生变化，分析重力异常随采空区深度、长度等等变化，以此研究分析微重力技术在采空区应用的可行性。

1 微重力观测方法基本原理

在矿区，重力场的分布通常与地下物质密度分布不均匀有关，物质密度的分布受到矿区采空区、矿产位置等分布影响。因此，研究地下物质密度分布不均匀引起的重力变化，为了解和推断矿区采空区分布提供了理论依据。微重力测量是一种精度极其高的重力测量方法，通常影响微重力测量精度的主要因素为仪器精度和高程测量精度。近年来，重力测量仪器的精度和高程测量的精度都得到了较好的提高，高精度相对重力仪(如CG-6型仪器)的测量精度能够达到±5 μGal，高程测量精度能够达到毫米级，仪器精度的提高使得利用这种方法进行采空区探查成为可能。

某个地质体所引起的重力异常的计算原理，都是基于牛顿万有引力定律。主要步骤如下：根据地质体的密度，得到地质体的剩余质量；计算其引起的引力位，然后再求出引力位沿重力方向的导数，从而得到该地质体引起的重力异常。

以地面上某一点O作为坐标原点，Z轴铅垂向下，即沿重力方向，X、Y轴在水平面上，见图1。

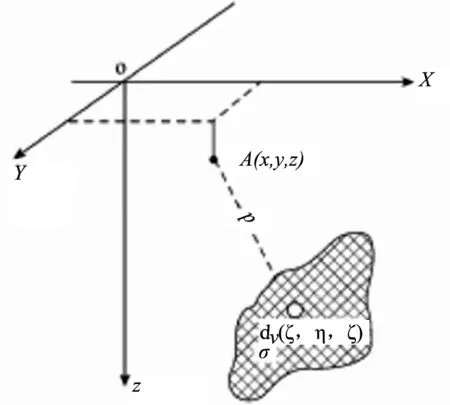
图1 任意形状地质体重力异常计算示意图

则地质体重力异常为：

(1)

2 模型计算和可行性分析

2.1 正演模型

为分析采空区特征对于地表重力异常的影响，以矩形采空区开采条件建立基准模型进行模拟计算。计算所采用的采空区的主要空间参数为：长度A、宽度B、高度C及埋深H。基本模型，见图2。

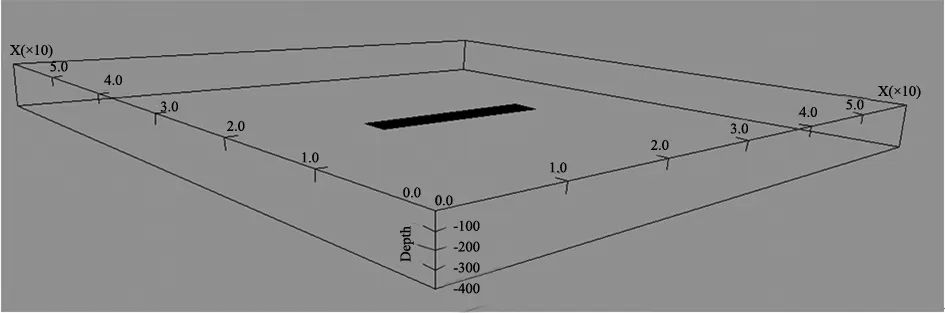
图2 采空区正演模型图

假设采空区产生的剩余密度为ρ=2 680 g/cm3。通过改变采空区宽度、深度和长度，正演地表观测的微重力异常变化，从而分析微重力技术的探测能力。

2.2 正演结果和可行性分析

基于牛顿万有引力定律，利用MATLAB软件编程实现正演算法，得到的正演模型所产生的重力异常如图3所示。在不同情况下，所产生的重力异常的最大变化量，从而分析微重力测量的探测敏感性，进行基于微重力测量的采空区探测可行性分析。

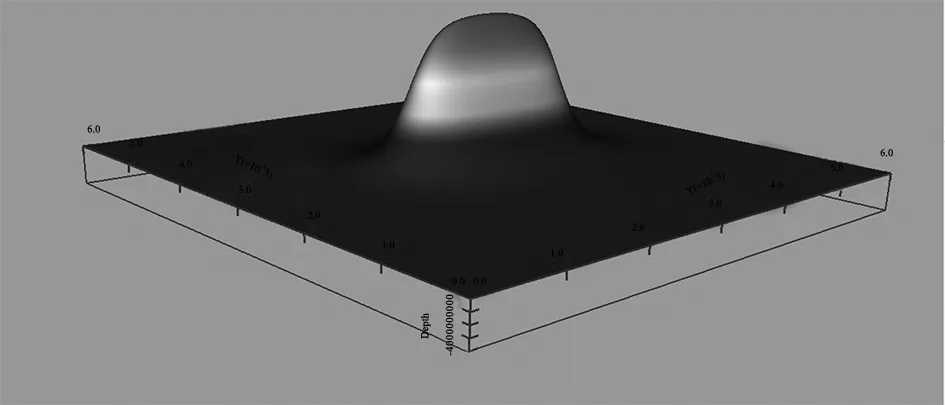
图3 三维正演结果示意图

首先，在宽度、深度尺度参数不变的情况下，分别计算了长度为1 000 m、1 500 m、2 000 m、2 500 m和3 000 m的长方体采空区模型，他们所产生的最大重力异常分别为：0.077 9 mGal，0.084 6 mGal、0.087 4 mGal、0.088 8 mGal、0.089 6 mGal，并统计了其能产生的异常最大值与采空区长度的关系，如图4所示。从该结果可以看出，当采空区达到1 000 m时，能够产生0.077 9 mGal的重力异常，且随着长度的增加，曲线趋于稳定，说明当采空区达到一定长度后，重力异常峰值大小趋于不变，在采空区中间地表达到最大重力异常值。

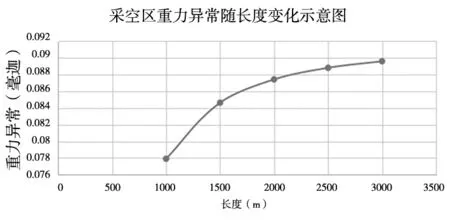
图4 采空区重力异常变化峰值随长度变化示意图

在长度、深度尺度参数不变的情况下，分别计算了宽度为100 m、150 m、200 m、250 m和300 m的长方体采空区模型所产生的最大重力异常，值分别为：0.044 9 mGal，0.066 6 mGal、0.087 2 mGal、0.107 2 mGal和0.125 8 mGal。从该结果可以看出，当重力异常峰值随采空区宽度增加而逐渐增大。通过其能产生的异常最大值与采空区宽度的关系可以看出，重力异常峰值与采空区宽度呈线性变化关系，说明重力异常受采空区宽度影响较大，见图5。

图5 采空区重力异常变化峰值随宽度变化示意图

在采空区长度、宽度尺度参数不变的情况下，分别计算了埋深为100 m、200 m、300 m、400 m和500 m的长方体采空区模型所产生的最大重力异常，其值分别为：0.22 mGal，0.128 7 mGal、0.087 4 mGal、0.064 6 mGal和0.050 2 mGal。从该结果可以看出，当重力异常峰值随采空区深度增加而逐渐减小。通过其能产生的异常最大值与采空区深度的关系可以看出，浅层时，重力异常峰值变化受采空区埋深影响较大；在深层时，重力异常峰值变化变小，说明重力异常探测能力在逐渐降低，见图6和表1。

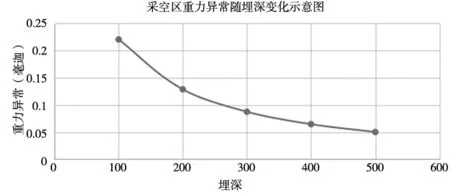
图6 采空区重力异常变化峰值随埋深度变化示意图

表1 正演成果数据汇总

3 总结

利用正演模拟完成了采空区长、宽、埋深变化对地表重力异常峰值的影响。从数值分析结果可以看出：

1)地表重力异常分布受到采空区影响，总体表现为地表重力异常与采空区的高度和宽度呈正相关，与开采深度呈非线性的负相关；

2)通过数值分析可以看出，在目前正演的参数框架下，重力异常均处于毫迦级别，因此在一定的测量误差情况下，探测精度为±5 μGal的微重力探测技术能够在这种情况下具有一定的可行性；

3)由于重力场是地下介质密度变化的综合影响结果，且实际情形中地下空洞呈非规则形状和离散分布，微重力方法仅仅能够综合反映地下空洞密度变化在地表的综合响应，较难直观地刻画地下空洞的离散发育形态，对于埋深较深的空区较难探测，需要通过进一步的微重力异常提取、分析、反演等处理实现空区的精细描述，是下一步工作的重要环节。