基于模糊自抗扰的四旋翼无人机设计

吕乐章 艾月 郝传斌 岳志睿 陈旭龙

（曲阜师范大学 山东省日照市 276800）

在过去的几年，四旋翼飞行器在军事和民用等场合得到了广泛的应用，从而成为众多学者的研究热点，它机械结构简单，灵活性强，具有垂直起落、自由悬停等优点。四旋翼无人机有空间内位置及姿态角共六个输出量，但只有四个电机输出转矩，并且系统各状态量之间存在互相耦合，容易受各种因素干扰，是具有四输入、六输出的欠驱动、非线性、强耦合系统[1]，因此四旋翼控制系统的设计在建模和控制上存在许多困难。

针对上述飞行器的控制问题， 国内外采用最多的控制方法是比例-积分-微分(PID)控制，此控制器简单且不依赖系统的模型，但是鲁棒性较差，难以取得很好的控制效果[2]。随着现代控制理论的发展，产生了很多基于现代控制理论的控制器，如：反步控制[3]、自适应控制[4]等，这些算法依赖精确的四旋翼模型，但四旋翼本身是个耦合系统，内部存在各种不确定性且容易受各种外部因素干扰，难以建立精确的模型。文献[5]采用神经网络算法调节PID 参数，以实现四旋翼系统的跟踪控制，但此控制算法复杂、参数冗杂，难以在工程上运用。

自抗扰控制技术(ADRC)是由韩京清研究院提出的，其继承了PID 控制的优点，不依赖被控对象模型[6]，同时借鉴了现代控制理论的部分思想，将无法精确建模的动态量、内部不确定性因素及外部干扰视为扩张状态，并利用非线性状态反馈进行补偿，从而实现抗干扰，具有控制精度高、超调量小、抗干扰能力强等优点，被广泛用于工程控制领域。

本文针对四旋翼强耦合和容易受外界因素干扰等问题，提出了一种结合模糊PID 控制技术和自抗扰控制技术的四旋翼控制方法。仿真实验结果表明，本文设计的四旋翼飞行器控制系统具有较强的抗干扰能力和鲁棒性，实现了对四旋翼飞行器对轨迹的跟踪。

1 系统模型建立

四旋翼飞行器由两个十字交叉、中心对称的机臂组成，飞行方式分为“十”字型和“X”字型两种结构，两种结构差别不大，本文选择“X”字型结构进行设计研究。结构形式如图1所示。

为了方便求出四旋翼的模型，假设四旋翼为对称的刚体，惯性坐标系的原点与机体坐标系的原点重合[7]，四旋翼的数学模型如下：

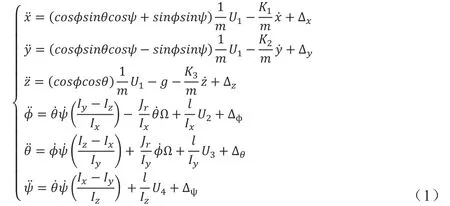
式中，m 为飞行器的质量，I 为惯性张量，x，y，z 是四旋翼

图1：四旋翼飞行器结构图

图2：自抗扰控制器结构图

图3：四旋翼系统控制框图

沿坐标轴平移的位置变量， φ 为横滚角，θ 为俯仰角，ψ 为偏航角。

U1、U2、U3、U4分别为垂直、滚转、俯仰、偏航控制量，与电机转速Ωi关系为：

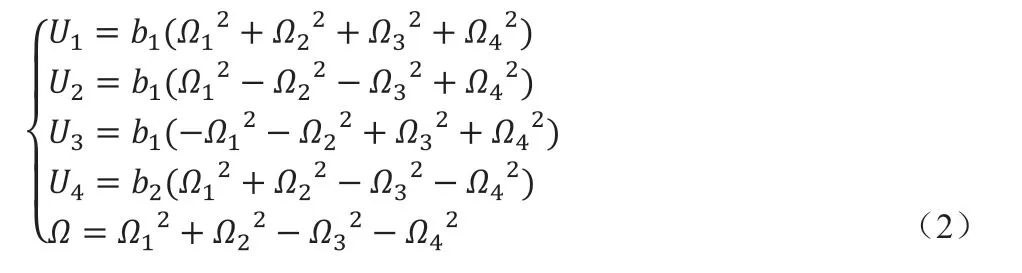
式中，Ωi为第i 个旋翼的转速，b1、b2分别为升力、阻力系数。

2 自抗扰控制基本原理

自抗扰控制器的是由PID 控制器演化而来，在继承PID 控制的优点的同时也弥补了传统PID 控制器的不足：增加跟踪微分器(TD)，解决了传统PID 控制器的响应速度快和超调量小之间不可兼得的问题；融合现代控制理论思想，建立扩张状态观测器(ESO)观测扰动；通过结合 “大误差小增益，小误差大增益”的经验建立非线性状态误差反馈控制律(NLSEF)，解决了PID 线性组合方式的不足。本文姿态回路所采取的自抗扰控制器为二阶自抗扰控制器，其结构如图2所示。

2.1 跟踪微分器

跟踪微分器(TD)为系统安排合适的过渡过程来减少输入信号v0突变引起的大幅度超调，并合理的提取出微分信号。通过对输入信号v0的处理，得到一个较缓慢的跟踪信号v1来跟踪输入信号，同时生成输入信号的微分v2来跟踪输入信号的微分。其离散化算法如下：

其中：r0为速度因子，h0为滤波因子。

式中，非线性函数fhan(x1(k)，x2(k)，r0，h0)定义为：

2.2 扩张状态观测器

ADRC 的核心是扩张状态观测器(ESO)，它将系统模型的不确定性和状态变量之间的耦合引起的内部扰动和未知环境引起的外部扰动看作系统的一个状态变量，并将它观测出来。其离散化算法如下：

2.3 非线性状态误差反馈

非线性状态误差反馈(NLSEF)将TD 跟踪的信号v1与信号的微分 v2与ESO 观测出的系统状态z1、z2之间的误差通过误差、误差微分的方式组合起来，其离散化算法如下：

其中fal(e2，a2，δ)取如下非线性形式：

利用扰动反馈控制律对z3进行补偿，最终得到控制量u：

3 四旋翼控制系统的控制器设计

图4：模糊PID 控制器结构图

将四旋翼的双闭环控制系统分为位置回路和姿态回路，四旋翼的位置信息作为位置回路的输入，位置回路的输出为姿态角作为姿态回路的输入，姿态回路的输出为垂直、滚转、俯仰、偏航的控制量，并通过式（2）作用在四个电机上，从而实现对四旋翼的控制。由于姿态回路对实时性和稳定性要求比位置回路更高，因此将姿态回路作为内环采用ADRC 控制器，位置回路作为外环采用模糊PID控制器。

由于四旋翼具有在空间内机体坐标系上x，y，z 轴三个方向的位置，以及姿态角φ、θ、ψ 共六个通道，却只有垂直、滚转、俯仰、偏航四个控制量，是一个欠驱动的系统，因此将六个通道分为4 个独立的控制回路：在机体坐标系z 轴方向上的位置控制采用模糊PID 控制，偏航角ψ 采用ADRC 控制，在机体坐标系x 轴方向上的位置控制与俯仰角θ 采用模糊PID-ADRC 串级控制，在机体坐标系y 轴方向上的位置控制与横滚角φ 采用模糊PID-ADRC 串级控制，系统控制框图如图3。

下面以四旋翼在x 轴方向的双闭环控制回路为例，来详细说明四旋翼抗干扰过程。

3.1 姿态环ADRC的设计

四旋翼系统的姿态回路为四旋翼控制系统的内环，跟踪位置回路的输出，将姿态回路的输出量作用在电机上，决定了四旋翼轨迹跟踪的速度和抗干扰能力。由飞行器动力学模型可知，四旋翼的三个姿态角之间互相耦合，且容易受外部未知的扰动干扰。姿态系统方程如下：

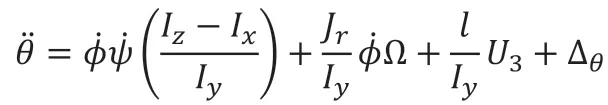
将四旋翼未建模部分与耦合部分和外部未知的扰动f(φ,θ,ψ,Δ)看作系统的一个状态变量，则俯仰角的数学模型可写成如下形式：

对系统建立扩张状态观测器：

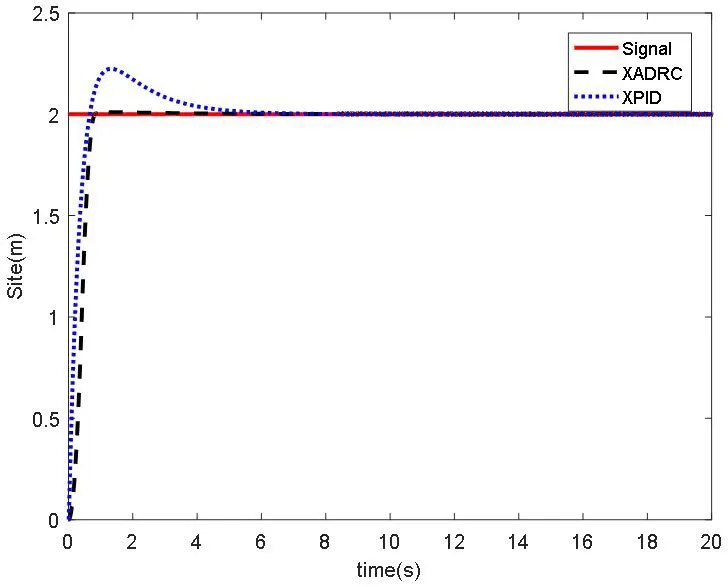
图6：未加扰动时的仿真结果

图7：加入扰动后的仿真结果

通过适当的调节此扩张状态观测器参数，便可以将俯仰角系统式（10）中的状态变量z1、z2、z3很好的估计出来，通过补偿扰动z3使得原系统变成线性系统，最后通过非线性状态误差反馈式（6）进行补偿，从而实现对姿态回路的控制。

3.2 位置环模糊PID的设计

四旋翼的位置回路为四旋翼控制系统的外环，将四旋翼的位置信息转换为姿态环的目标姿态角，决定了四旋翼轨迹跟踪的适应性和精度。由于位置回路为非线性系统且PID 无法实时调整参数，因此采用模糊PID 作为位置回路的控制器来提高位置回路的适应性和精度。

模糊PID 控制器由模糊控制器和PID 控制器两部分组成，通过输入目标位置和当前位置的偏差e 以及偏差的微分Δe，根据给定的模糊规则进行模糊推理，最后进行解模糊，得出PID 的三个参数的修正值Δ Kp、Δ Ki、Δ Kd，使得PID 控制器能够实时调整参数。模糊PID 的控制框图如图4所示。

3.2.1 PID 控制器

PID 控制器根据系统的偏差，利用比例-积分-微分三部分的作用得到输出量来消除误差。在位置回路中，将位置信息的偏差作为输入，通过PID 控制律得到俯仰角θ 作为内环的输入，PID 控制律如式（12）：

式中： Xtar为目标位置，Xnow为当前位置，Kp、Ki、Kd为经过模糊控制器整定后的参数。

3.2.2 模糊控制器

模糊控制器分为模糊化、模糊推理、解模糊三部分。本文将输入变量e、Δe 和输出变量Δ Kp、Δ Ki、Δ Kd的论域均选取为{-3,-2,-1,0, 1,2,3}，模糊子集设为{NB, NM, NS, ZO, PS, PM, PB}。采用高斯型隶属函数作为输入变量的隶属度函数, 采用三角形隶属函数作为输出变量的隶属度函数，并用Mamdani 法则来作为模糊系统的逻辑推理方法，其模糊规则如表1。采用的解模糊的方法为重心法，通过模糊控制器使PID 控制器能够根据环境实时调整参数，提高了四旋翼飞行器系统的适应性。模糊控制器的结构如图5。

4 仿真实验

为了更好的比较出本文设计的模糊自抗扰控制器的控制效果，我们分别采用模糊PID-ADRC 控制器和串级PID 控制器对无人机系统进行位置跟踪实验、抗扰性实验。本文以位置x 为例，通过Matlab 仿真并通过对比分析实验结果，以此检验本文设计的模糊自抗扰控制器的快速响应能力、抗扰性能力。

实验过程中设定积分步长h=0.001，位置回路所选取的模糊PID 控制器初始参数为kp0=0.50，ki0=0.001，kd0=0.001，姿态回路所选取的ADRC 控制器参数如表2所示。四旋翼的起始位置状态为x=0, y=0, z=0,起始姿态的俯仰角θ、横滚角φ、偏航角ψ 都为零，设定目标位置的理想值为幅值为2 的阶跃信号，位置x 的跟踪效果如图6所示。

为了更好的验证模糊自抗扰控制器的抗扰能力，我们采用方波和正弦波模拟外界力矩扰动，在t=5s 时，加入幅值为0.5m，宽度为3s 的方波作为扰动；在t=11s 时加入y=0.5sin(1.6πt)的正弦波作为扰动。仿真结果如图7。

从图6 的仿真结果来看，基于模糊PID-ADRC 算法控制下的响应过程中调节时间较短，在t=1s 时，就能达到稳定状态，快速的跟踪设定的期望值x 坐标2，并且最大值在x=2 附近，超调量很小，波动范围在0.01～0.05 之间，没有出现振荡现象。而串级PID在t=6s 时才趋于稳定，调节时间长。并且在t=1s 时到达第一个峰值2.25m，超调量为12.5%左右。通过以上对比分析可见，基于模糊PID-ADRC 算法的控制系统能够使得系统快速跟踪设定轨迹，减少超调量和调节时间。

图7 为在两种扰动作用下的基于串级PID 算法和基于模糊PID-ADRC 算法控制的系统响应曲线。在加入方波和正弦波干扰后，在t=5s 和t=11s 基于串级PID 控制系统开始出现振荡，最大峰值为2.4m，且不能快速跟踪期望的位置坐标，对外部扰动的抑制能力较弱。而基于模糊PID-ADRC 算法控制系统能较好的跟踪期望的位置坐标，响应曲线没有出现大幅波动，响应无超调，系统调节时间短。通过以上对比，模糊自抗扰控制系统较串级PID 控制系统更加稳定，受扰动的影响小。因此基于模糊PID-ADRC 算法的四旋翼控制效果更好，更加利于稳定飞行。

5 结论

本文以四旋翼为控制对象，设计的一种结合模糊PID 控制技术和自抗扰控制技术的控制方法实现了对四旋翼飞行器系统的高品质控制，模糊PID 控制器提高了位置回路的精度和适应性，自抗扰控制器实现了对姿态回路的解耦并提高了系统的抗干扰能力，通过系统的仿真实验，并与串级PID 控制器的控制结果进行对比，验证了本设计较串级PID 控制具有一定优势。本设计不依赖精确的系统模型，响应速度快，抗扰能力强，有效的提升了四旋翼飞行器的抗干扰能力及轨迹跟踪能力，具有实际应用的价值。

表1：模糊规则表

表2：ADRC 参数