面向边界控制的城市交通子区划分研究

万思佳 王景升

摘要：为了获得面向边界控制的交通子区，文章通过计算关联度将路网初步划分为一定数量的子路网，提出一种基于初始划分的凝聚聚类算法进行子区逆向合并，并引入密度均匀度和平均分割权重的概念，以包头市青山区路网为研究对象进行评估分析。结果表明该方法可以优化子区的密度均匀度，对路网进行合理划分。

关键词：子区划分;宏观基本图;边界控制;交通工程

0 引言

随着信息技术的发展和大数据算法的不断完善，电子警察、微波检测器等交通检测技术被广泛运用，获取大规模路网的各种信息变得更加便利。Geroliminis[1]通过分析日本横滨路网的线圈检测器数据发现路网的加权平均流量和路网的加权平均密度存在一定线性关系，并由此提出了宏观基本图（MFD）的概念。之后，大量学者将其应用于路网边界控制。子区划分作为边界控制的基础有着重要意义，Maziloumain[2]等利用仿真软件进行试验，指出了密度分布的均匀程度是影响MFD的重要因素。在此基础上Ji[3]等提出以ncut法为初始划分方法，通过逆向合并密度相近的相邻子区调整划分区域，获得子区内部密度方差最小化的子区。刘澜[4]等对该方法进行了改进，运用贪婪算法逆向合并子区，寻找具有最优拟合度的MFD子区，但该方法的目标是确定一个宏观基本图拟合程度高的子区。李刚奇[5]等从宏观层面，运用图像分割的方法，以路段为对象，提出了基于路段交通流密度的城市子区划分方法。

以上面向边界控制的子区划分方法仅将路段的密度作为划分标准进行研究，忽略了交叉口的关联性。交叉口关联度指标主要用于表征两个交叉口相互影响的程度，依据关联度把路网划分成若干个相对独立的交通控制区域，即使某一个子区由于偶发性事故处于运行效率低的状态，也只是对该子区内其余交叉口的协调控制影响较大。在此基础上，本文提出以关联度模型为初始划分基础，以子区内交叉口关联性较大且密度分布均匀为目标的子区划分方法。

1 子区划分方法

本文提出的子区划分方法主要分为两步：

（1）利用Whitson模型计算相邻交叉口的关联度，并依据协调阈值将路网初步划分为一定数量的子区。

2 实验

2.1 路网描述

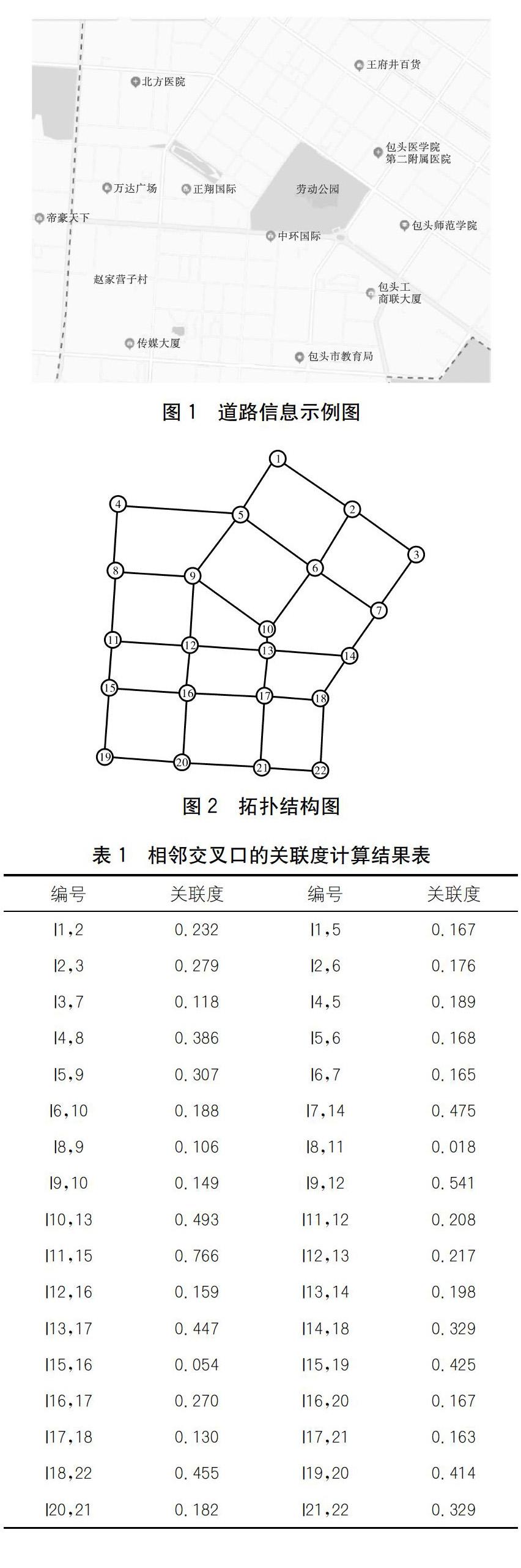
选取包头市青山区的主要路网为研究对象，其中道路信息如下页图1所示。整个路网包括22个交叉口，68个路段，最长的信号周期为160 s，交叉口上都覆盖了交通检测器。对路网内的22个交叉口进行编号，道路拓扑结构如下页图2所示。实验以2019-06-17的电子警察数据来做研究，统计时间为5 min。

2.2 路网子区划分

利用Whitson模型计算出相邻交叉口之间的关联度结果如下页表1所示。

根据计算出的相邻交叉口关联度对整个路网进行初步划分，路网被初步划分为10个子区，划分结果如图3（a）所示。与相邻交叉口关联度较小的交叉口容易被单独划分为一个子区，单个交叉口形成子区会增加管理负担，不利于边界控制。通过合并平均密度相似的子区调整子区划分的结果，整个合并过程如图3（b～i）所示。表2显示合并过程中路网平均密度均匀度的变化，当子区数量为3时路网平均密度均勻度最小，所以最优小区划分数量为3。

2.3 结果分析

基于前人的研究，本文假设MFD的形状为二次项，以路网加权平均密度kw（单位为veh/km）为横坐标，路网加权平均流量qw（单位为veh/h）为纵坐标进行拟合。采用二次多项式拟合的MFD应该满足以下条件[9]：

（1）MFD曲线应该存在极值，并且极值为正;

（2）考虑实际交通情况，路网密度为0时流量也为0，因此利用二次多项式拟合得到的 MFD方程的常数项应该为0。

子区划分结果和对应子区宏观基本图的基本性质如表3所示。

由于路网数据有限，被划分到子区一内的交叉口较少。刘澜[4]等人的研究侧重于获得MFD拟合程度最大的单个子区，而本文的方法获得的三个子区都可以得到拟合度较高的MFD。其中拟合度最高的子区三由两条主干道组成，交叉口分布较规则，且交叉口间距较大，车队在该子区内受信号控制影响相对较小，密度分布更加均匀，更容易形成拟合度高的宏观基本图。

2.4 对比实验

为了验证该方法在子区划分中的优越性，运用归一化分割的方法对相同条件下的路网进行划分，以路网平均密度均匀度为确定最优子区划分数量的标准，当子区数量为3时路网平均密度均匀度最小，归一化分割法子区划分结果如表4所示。本文采用的方法平均分割权重W=0.180 875;归一化分割法方法获得的平均分割权重W′=0.232，子区间边界路段的关联度更低。目前大部分学者基于宏观基本图理论运用归一化分割法算法进行路网子区划分时仅从路网空间密度分布出发，忽略交叉口关联度，如表4中交叉口18和交叉口22关联度较高却被划分到两个子区，在进行边界控制的时候两交叉口相互影响会加大信号控制的难度。

3 结语

路网边界控制研究中，子区间边界路段是调节子区交通状态的关键，通过控制经过边界路段的车辆数可以调节相邻子区的交通状态，均衡调节整个路网的交通流。本文考虑到交叉口间关联度对边界控制的影响，首先利用Whitson模型进行初步划分，然后通过融合算法提高密度空间均匀度，并通过实例分析证明了该方法的有效性，为进一步研究基于MFD的边界控制奠定了基础。同时，得出以下结论：

（1）提出考虑交叉口关联度的MFD子区划分方法，与之前被广泛运用的归一化分割方法进行对比发现，在将路网划分为密度均匀的子区的同时，也可以将关联度较大的交叉口划分到相同子区，有利于边界控制和子区内部的协调控制。

（2）在构建宏观基本图时发现，不同子区构建的宏观基本图所确定的临界加权平均密度和最大加权平均流量不同，即不同子区拥堵状态有差别。下一步可以考虑以多子区状态一致为目标，构建多子区协同控制模型，快速缓解子区的拥堵状态，实现整个路网交通流的均衡分布。

参考文献：

[1]Nikolas Geroliminis，Carlos F. Daganzo. Existence of urban-scale macroscopic fundamental diagrams：Some experimental findings[J/OL]. Transportation Research Part B，2008，42（9）.

[2]Amin Mazloumian，Nikolas Geroliminis，Dirk Helbing. The spatial variability of vehicle densities as determinant of urban network capacity[J].Philosophical Transactions of the Royal Society A-AAa thematical Physical and Engineerirg Science，2010，368（1 928）：4 627-4 647.

[3]Yuxuan Ji，Nikolas Geroliminis. On the spatial partitioning of urban transportation networks[J]. Transportation Research Part B，2012，46（10）：1 639-1 656.

[4]劉 澜，卢维科，胡国静，等.面向边界控制的路网小区划分[J].中国公路学报，2018，31（11）：186-196.

[5]李刚奇，赵娅丽. 基于宏观交通理论的交通控制子区划分方法[C]. 中国智能交通协会.第七届中国智能交通年会优秀论文集——智能交通技术，2012.

[6]冯远静，单 敏，乐浩成，等.绿波协调控制的子区动态划分算法[J].控制理论与应用，2014，31（8）：1 034-1 046.

[7]闫 安.城市交通路网节点关联性研究及应用[D].北京：北京交通大学，2019.

[8]别一鸣，王琳虹，王殿海，等.城市路网交通控制子区动态划分策略[J].中国公路学报，2013，26（6）：157-168.

[9]金 盛，沈莉潇，贺正冰.基于多源数据融合的城市道路网络宏观基本图模型[J].交通运输系统工程与信息，2018，18（2）：108-115，127.