高速燃驱一拖二机组动力学特性分析*
2020-01-18温鹏昊张志莲
孟 波 冷 雪 温鹏昊 张志莲 马 壮
(1.北京石油化工学院机械工程学院;2.北京化工大学石化学院)
0 引言
西气东输对于调整我国能源结构、促进环境状况改善具有重大意义。随着输气量的增加及输送安全性的考虑,燃驱压缩机组成为西气东输沿线压气站供能的首选方式[1-2]。由于地理条件、水电等外部因素限制,以及输气量、输气速度等内部因素干扰,动力涡轮工作条件复杂。动力涡轮变工况运行时,压气机转子系统常常发生机械振动,导致机组的工作效率降低,严重情况下会使元件断裂、转子失稳,造成重大事故。因此,对西气东输动力涡轮燃驱机组进行转子动力学分析将为转子系统优化设计、安全保障和延长寿命提供理论和技术上的支持[3]。
测量动力涡轮功率的水力测功机单台工作包线无法满足转速要求,只有采取两台同型号的水力测功机轴向串联的方式,扩大测功机的包线才能满足要求。两台水力测功机串联同时使用在国内尚属首次,此研究将实现我国工业燃气轮机领域关键产品的重大突破,填补国内空白。对于此类高速转子系统,采取适当措施减小转子的不平衡量、降低临界转速和增大阻尼,都可以达到减小转子振动幅值的目的。而在动力涡轮总体结构设计已经确定的前提下,采用弹性支撑和阻尼器等减振方式,成为了最为有效和可行的方法[4]。本文中动力涡轮驱动的水力测功机转子就是采用了这种减振方式。
本文以某型高速燃驱一拖二机组(高速动力涡轮—1#水力测功机—2#水力测功机)为研究对象,由于轴系支撑系统由结构钢架和基座组成,支撑系统弹性不能忽略。因此,本文基于传递矩阵法建立了复杂转子—轴承—基础系统转子动力学模型,对其三次支撑结构下的动力学特性进行了数值计算,揭示了该类型轴系不同支撑刚度下的不平衡响应特性及转子间的相互影响规律,为该类机组的故障诊断及现场动平衡提供依据。
1 轴系有限元动力学建模
1.1 轴系运动方程
目前,转子动力学常用的计算方法是传递矩阵法和有限元法。传递矩阵法由于编程简单、占内存少、运转速度快,被广泛应用于转子系统计算中。Thomson将传递矩阵法应用到一般线性系统振动问题,针对求解高速大型转子数值不稳定的问题,而后提出的Riccati传递矩阵法保留了原方法的全部优点,提高了稳定性和计算精度[5-6]。沈存五、葛庆等人用传递矩阵法计算分析了一种复杂的具有中心拉杆结构的转子—轴承系统,并将计算结果与实验结果对比,证明传递矩阵法可以解决这种复杂结构的转子—支撑系统的临界转速计算问题[7-8]。项松、王克明等人利用传递矩阵法对某转子系统动力特性进行了计算分析,分析过程中改变不同位置的支撑刚度,得到轴承支撑刚度对该转子临界转速的影响程度[9]。传递矩阵法与机械阻抗、直接积分等其他方法相配合,还可以求解复杂转子系统的问题。
本文基于此采用传递矩阵法建立转子轴系的运动方程

其中,M,C,K是系统的质量、阻尼、刚度矩阵;z是系统广义坐标矢量;F是作用在系统上的广义外力。
考虑到转子轴系结构的特殊性,将式(1)加以变形,得到轴系的动力学模型:

其中,c,k为支撑及其他边界上的阻尼、刚度矩阵。
本文首先采用传递矩阵法建立典型构件两端截面状态矢量之间的传递关系式,再利用连续条件,就可以得到整个转子两端截面的状态矢量之间的关系式。通过对能满足边界条件的涡动频率的搜索,得到转子各阶临界转速。计算转子在给定转速下由不平衡质量激励引起的振动,就可以求得转子的不平衡响应。
1.2 轴系有限元模型

图1 动力涡轮一拖二机组结构示意图Fig.1 Schematic diagram of the gas turbine one-to-two unit
动力涡轮一拖二机组的结构示意图如图1所示,为了扩大测功机的工作包线以实现测量目的,轴系机组由一个动力涡轮和两个水力测功机组成,动力涡轮和1#水力测功机之间采用重型叠片挠性联轴器连接,1#水力测功机和2#水力测功机之间采用膜片联轴器连接。机组出厂前,在动力涡轮和水力测功机机组上共布置8个振动测点,分别为:低压压气机水平测点、高压压气机水平测点、动力涡轮水平和垂直测点、1号水力测功机前测点、1号水力测功机后测点、2号水力测功机前测点、2号水力测功机后测点。由于水力测功机的内部结构复杂精度要求高,计算关注点为图2中从左至右的1#水力测功机前轴承、1#水力测功机后轴承、2#水力测功机前轴承、2#水力测功机后轴承。
采用Dyrobes-Rotor专业转子动力学分析软件,建立了轴系机组整机有限元模型,如图2所示。在轮盘、集中质量、轴承所在的位置以及轴截面发生突变的位置处均应划分出节点单元,在振动弹性线变形比较剧烈的地方,应多分几段。动力涡轮有两个转子,水力测功机有九个转动单元,分别计算出质量和转动惯量,模型中采用简化的质量盘来代替。建立的转子全长为7.002 6m,总质量为2 734.9kg,共分为170个主单元、21个盘单元,轴承位于28,44,115,129,153,167节点。

图2 动力涡轮一拖二机组轴系有限元模型Fig.2 Finite element model of the shafting system of the power turbine one-to-two unit
2 轴系动力学特性分析
2.1 轴系临界转速的计算与分析
2.1.1 单转子临界转速的计算与分析
当转子旋转速度与转子系统的自振频率相等时,由于质量偏心产生的周期性离心惯性力使转子发生强烈的共振,转子发生共振时的转速即为临界转速。本文首先分析本机组单转子系统的临界转速。

图3 动力涡轮一阶临界转速及振型Fig.3 First-order critical speed and vibration mode of gas turbine
图3为动力涡轮一阶临界转速及振型图,由图可知,其一阶临界转速为3 547r/min,而其实际工作转速为3 000r/min,一阶临界转速大于工作转速,为刚性转子,单独运转时不会发生共振。动力涡轮第一阶振型以左悬臂轴端振动为主,且左悬臂轴端振动位移最大。
图4为水力测功机一阶临界转速及振型图,由图可知,其一阶临界转速为9 757r/min,远大于实际工作转速8 000r/min,为刚性转子,单独运转时不会发生共振。水力测功机第一阶振型为平移振型,最大振动位移发生在轴中心的位置。

图4 水力测功机一阶临界转速及振型Fig.4 First-order critical speed and vibration mode of hydraulic dynamometer
2.1.2 轴系临界转速的计算与分析
燃驱一拖二机组在实际运转中是一多跨转子,多跨轴系与单跨转子相比而言,其振型和临界转速有很大区别。本文基于此计算了机组轴系前三阶无阻尼临界转速,如图5所示。单跨转子及轴系各阶临界转速如表1所示。
2.2 轴系不平衡响应的计算与分析
不平衡分析的目的是确定运转时由不平衡激起的临界转速和相关的放大系数,通过计算不平衡响应,可预测它们在工作时的振动值。
2.2.1 轴系支撑系统的刚度设定
转子—轴承系统的总刚度主要与轴的支撑系统(包括基础或支撑结构、底座、机器构架和轴承箱等)有关,针对分析动力涡轮一拖二机组横向动力特性的计算需要,必须注意轴承支撑刚度和基座支撑刚度的正确匹配关系。
轴承支撑刚度均为实际测量刚度,动力涡轮前、后轴承支撑刚度分别为5.6×108N/m、3×1010N/m,水力测功机四个轴承支撑刚度均为4.55×108N/m。

图5 轴系前三阶临界转速及振型Fig.5 The first three critical speeds and modes of the shafting
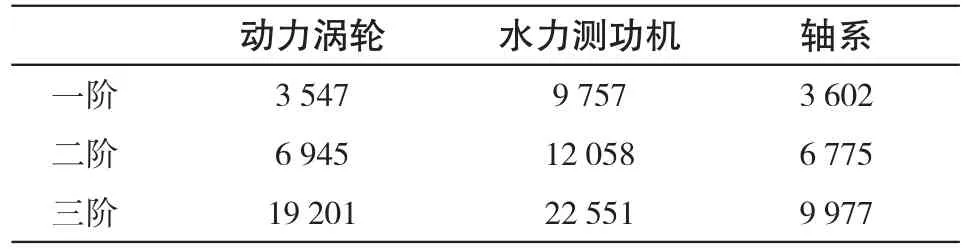
表1 单跨转子及轴系各阶临界转速(r/min)Tab.1 Critical speed of each step of single-span rotor and shafting(r/min)
基座支撑刚度取决于基座支撑结构,水力测功机底座未改造前,基座支撑刚度小于8.9×108N/m。水力测功机底座第一次改造时,主要将底架内部横向筋板连成一体,填充钢丸,外部凹槽内的筋板连成一体,侧边框格内交叉焊接螺纹钢筋,并填充C30混凝土,水力测功机基座支撑刚度等于8.9×108N/m,同时动力涡轮基座支撑刚度增大到3×1010N/m。水力测功机底座第二次改造时,底架由现有的焊接结构改为铸造结构,高度由950mm降为200mm,同时将地面基础相应抬高770mm,水力测功机底架上加工有横向T型槽用于安装水力测功机,基座支撑刚度大于8.9×108N/m,具体参数如表2所示。

表2 三次试车基座支撑刚度值(N/m)Tab.2 Base support stiffness values(N/m)for three tests
2.2.2 轴系不平衡量的施加
由于加工精度和工作磨损的原因,转子系统不可避免地存在质量不平衡。不平衡量用分解的方法施加在临界转速计算中振型最不利的位置和相位角上。
画师以简练且严谨流畅又干净的线条绘制了众多生动的形象,这些形象按不同身份,性格特征,和表情变化而刻画出不同的人物形象,做到多样而不雷同,线条的组织疏密有致,在刚柔相济的变化中创造了美丽和谐的装饰性效果,也正因此它与敦煌壁画产生较大的反差,因此在瓷画上用颜色釉创作时也应以线条为主,色釉为辅,构图更需要理性化和设计性构图,由于陶瓷表现的空间有限,对于大型壁画的创作就需要理性化的设计,使之与器型相吻合,产生和谐美,对点、线、面、形等造型要素,做出合理的布局,精确的安排。
在此转子系统中,不平衡量值按方程(3)计算。

式中,U为作转子动力学响应分析的输入不平衡量,g·mm;N为最大连续运转速度;W为轴颈处静载荷,kg;或在轴端处出现的最大偏差的弯曲振型悬臂质量,kg。
由临界转速的计算可知,动力涡轮的一阶振型为锥形,不平衡量的计算值为11.17kg·mm,施加在左端悬臂处5号节点。1#水力测功机和2#水力测功机的一阶振型为平移振型,不平衡量的计算值为5.136kg·mm,分别施加在轴中心位置的122和160节点处。
2.2.3 轴系不平衡响应的计算与分析
为了计算转子系统在不同支撑条件下的振动峰值以及影响系数,研究支撑系统对不平衡量的敏感程度,本文依据API617标准计算隔离裕度SM评价轴系稳定性。本转子系统的隔离裕度公式按方程(4)计算。

式中,AF为放大系数;SM为隔离裕度,SM在计算值和16间取较小值。
图6为1#水力测功机左轴承处的响应,4 900r/min时,SM的计算值为16.78,取SM=16。即其隔离裕度为16%,轴系工作转速6 100r/min落在了隔离裕度[4 900×(1-16%)4 900×(1+16%)],即[4 116 5 684]外,根据API617规定,1#水力测功机左轴承不平衡响应验证合格。

图6 1#水力测功机左轴承处的振动响应Fig.6 Vibration response of the left bearing at 1#hydraulic dynamometer
图7为1#水力测功机右轴承处的响应,SM的计算值为16.77,取SM=16。右轴承和左轴承的情况类似,在4 900rpm产生振动峰值,但是工作转速落在了隔离裕度之外,右轴承不平衡响应验证合格。

图7 1#水力测功机右轴承处的振动响应Fig.7 Vibration response of the right bearing at 1#hydraulic dynamometer
经计算,2#水力测功机工作转速落在隔离裕度之外,符合API617标准。
针对水力测功机底座支撑结构的两次改造,计算不同支撑刚度对轴系不平衡响应的影响,图8~11为三次计算的各测点对比图。

图8 1#水力测功机前轴承处三次计算值Fig.8 Three calculated values of the front bearing of 1#hydraulic dynamometer

图9 1#水力测功机后轴承处三次计算值Fig.9 Three calculated values of the rear bearing of 1#hydraulic dynamometer

图10 2#水力测功机前轴承处三次计算值Fig.10 Three calculated values of the front bearing of 2#hydraulic dynamometer

图11 2#水力测功机后轴承处三次计算值Fig.11 Three calculated values of the rear bearing of 2#hydraulic dynamometer
从图中可以看出,随着水力测功机基座轴承刚度的逐渐加大:
1)对于1#水力测功机前轴承:在5 500r/min以前,支撑刚度小于8.9×108N/m的基座动力响应最小,支撑刚度接近刚性的基座动力响应次之,支撑刚度等于8.9×108N/m的基座动力响应最大;在5 500r/min以后,随着基座支撑刚度的增大动力响应逐渐减小。在4 700r/min左右出现振动峰值,工程应用时应尽快通过此运行转速。
2)对于1#水力测功机后轴承,这种变化趋势与前轴承相反,在4 000r/min以前,随着基座支撑刚度的增大动力响应逐渐减小;4 000r/min以后,支撑刚度小于8.9×108N/m的基座动力响应最小,支撑刚度接近刚性的基座动力响应次之,支撑刚度等于8.9×108N/m的基座动力响应最大。
3)对于2#水力测功机前后轴承,支撑刚度接近刚性的基座动力响应最小,支撑刚度小于8.9×108N/m的基座动力响应次之,支撑刚度等于8.9×108N/m的基座动力响应最大,并在工作转速6 100r/min时的动力响应最大。
轴系实际工作转速在6 100r/min,工作转速处的振动量均满足API617动力学部分的设计要求,可以投入使用。
3 结论
1)动力涡轮和水力测功机单跨转子在其工作转速下,均为刚性转子,根据API617标准,不会发生共振。
2)燃驱一拖二多跨轴系一阶振型为动力涡轮主导,轴系的一阶临界转速高于单个动力涡轮的一阶临界转速。这是因为在组成轴系时,单跨转子在轴端通过联轴器受到其他转子的约束,提高了刚度。
3)通过改变基座钢架结构增加其刚度,减小支撑系统刚度对不平衡响应的敏感程度,计算可知,支撑系统刚度大于3×1010N/m后,振动峰峰值小于6.1mm,满足出厂要求。
4)在国内首次采用两台水力测功机串联工作的方式,并对其组成的高速燃驱一拖二机组在三种支撑结构下的动力特性进行了计算和分析,为该类机组的现场动平衡提供参考和依据。两台水力测功机串联使用在国内尚属首次,此研究将实现我国工业燃气轮机领域关键产品的重大突破,填补国内空白。
