基于改进的遗传算法的天然气管网系统运行优化*

高建丰 金卷华 王焱 何笑冬 周韶彤 黄光曦

1浙江海洋大学石化与能源工程学院

2临港石油天然气储运技术国家地方联合工程实验室

3中国石油天然气股份有限公司天然气销售西部分公司

天然气管网系统是一个组成非常复杂、造价较高的输气系统，随着天然气输配调控和自动化技术的不断发展，其系统设计的科学性直接影响着城市的天然气使用和工业用气安全。提高天然气管网的系统安全性和经济效益，实现管道的安全运行、节能减排，一直是科学研究中的重大目标。随着计算技术的高速发展一些智能算法逐渐应用在管道系统优化设计方面，遗传算法（Genetic Algorithm，GA）作为其中之一是由HOLLAND 教授首先提出来的[1]，该算法是通过参考生物界的自然进化演变而来的寻找最优解的方法。首先需要完成从个体表现型一一对应到基因型的编码操作，在随机产生初始第一代种群后，根据自然界适者生存的理论，保留优者淘汰劣者，每一代按照适应度值大小选择合适的个体进入下一代遗传，使得后代种群比上一代更加适应环境，判断个体是否符合收敛准则，如不满足则重新进行新一轮的交叉和变异的迭代遗传操作，直至找到符合要求的最优个体，即为模型求得的近似最优解[1-3]。

天然气管网系统的运行技术已经基本成熟。目前，国内外研究主要集中在如何对天然气管网系统模型进行更深一步优化，提高模型的求解速率，对非稳态系统运行进行优化等方面。El-MAHDY 等将遗传算法应用于天然气管网参数优化，通过多次运算对比，得到管网最小成本及最佳管径[4]；李卫华等建立了天然气集输管网的参数优化模型，利用遗传算法加快了系统的求解速度[5]；张培培等采用遗传算法对天然气管径进行优化，实例计算说明遗传算法是一种可取的优化算法[6]；郑凤等采用复合形法对天然气管网系统优化模型进行研究，实际应用证明该方法是有效的[7]；殷建成等以网络最小费用流理论结合动态规划算法对模型进行优化求解，证明了该算法的实用性[8]；杨毅等采用线性化算法对模型进行优化计算，表明了算法的优越性[9]；李自立等利用遗传算法对气田集输管网整体优化，得到的优化结果比传统分级优化投资费用更少[10]。通过学习前人的研究发现，遗传算法能较好地解决一些优化难题，但是该算法在求解计算时容易得到局部最优解，不利于找到真正意义上的最优解，故本文加入了模拟退火的概念。因为遗传算法具有良好全局搜索能力，模拟退火算法具有能够无穷接近最优解的能力，因此有效地将这两种算法融合起来，以提高算法搜索效率并防止局部最优现象发生，从而达到最大输气量的最优准则，实现算法的改进和优化[11]。本文的天然气管网系统的优化设计是在考虑安全稳定运行的基础上，以天然气输配流量为目标函数建立输气管网模型，利用基于整数编码的遗传算法求解，用模拟退火罚函数来转化约束条件，改进算法的运行效率。通过实例计算，改进的遗传算法的优化流量结果普遍好于基本遗传算法，验证了该模型能够充分利用天然气管网的输配能力，改进的算法是切实可行有效的，能够为今后的天然气管网系统优化提供一定的生产指导[12-13]。

1 输气管道优化设计模型的建立

1.1 优化设计问题

随着天然气管网系统自动化水平的提高，很多管网系统可以根据其运行环境自动调节控制系统，以此来调控管道的运行，使天然气管道在允许的安全范围内达到最大输配能力。在满足一定约束条件的情况下，本文基于改进的遗传算法，通过选择适应度高的染色体进行交叉和变异的操作，判断个体是否符合限定准则，若不满足则不断迭代循环重复上述操作直到求得问题的最优解，最终各节点得到的最优解即为所能达到的最大流量，从而达到优化的效果[13-16]。

1.2 数学模型构建

为了提高天然气管网系统的运行效率，在安全稳定运行的基础上，在满足一定约束条件的前提下，建立了优化的输气管网数学模型[9-13]，实现系统流量最大化。

目标函数为

式中：N为天然气管网系统中的节点总数；Qi为第i个节点输入的天然气流量，104m3/d。

节点流量平衡约束条件满足公式

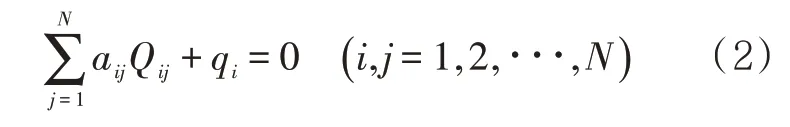
式中：aij为系数，其中aij=0 表示节点i和j无关，aij=1 表示节点i和j相关且从节点输入，aij=-1 表示节点i和j相关且从节点输出；Qij为节点i和j之间流量的绝对值，始终为正数；qi为节点i与外界转换的流量。

管道内气体稳定流动约束条件满足公式

式中：Q为标准状况下经过管道的天然气流量，m3/s；D为管道直径，mm；pS为管道的起点压力，MPa；pE为管道的终点压力，MPa；H为管道起始端与终端之间的高度差，m；λ为气体摩阻系数；；Z是气体的压缩系数；R为通用气体常数，8.314 3 kJ/(kmol·K)；T为气体流动的平均温度，K；L为管长，m。

管径、流量、节点压力、管段压力等约束条件满足公式

式中：Dimin、Dimax分别为管径的下、上限；qimin、qimax分别为通过节点i气体流量的下、上限；pimin、pimax分别为节点i压力的下、上限；pjmin、pjmax分别为管段j压力的下、上限。

可见，上述优化模型需要解决的问题是非线性的，且存在离散变量和连续变量的复杂情况，而求解非线性方程组不是一个容易的问题，没有一种特别有效的方法。本文在遗传算法的基础上加入模拟退火概念，将这两种算法有效地进行结合，以达到高效率搜索最优解的目的，从而实现管网系统输配量最大化。

2 基于改进的遗传算法的模型求解

2.1 基本遗传算法

遗传算法（GA）是通过借鉴生物的优胜劣汰进化规律，将问题的求解变量称为个体，并对其进行编码，翻译成染色体，然后随机构成初始种群，根据适者生存的原则，保留优者淘汰劣者，对个体以选择、交叉和变异等方式不断进行迭代循环，直至找到最优解的方法[1]。遗传算法执行选择、交叉和变异的方式进行操作情况可以进一步解读为：

（1）选择。在实际操作中，主要是在特定环境下选择出可以较好适应环境的染色体，让该个体不断繁衍。HOLLAND 教授的轮盘赌选择方式是适应值高的个体被选中的概率较大[1]，这样不仅可以保证下一代中一定包括最适合环境的个体，同时也保证了最优个体进入下一代的可能性更高。假设第t代种群P(t) 中共有N个染色体xi(1 ≤i≤N)，各染色体的适应度为f(xi)，则染色体xi被选中的概率计算公式为

（2）交叉。所有染色体随机配对的过程中，均会产生若干个交叉点，按照单点交叉方式以交叉概率交换部分基因，形成新的染色体。具体的步骤是将上一步选择的个体，随机两两互相配对，并把这两条染色体从某一位置切断，然后拼接在一起，从而生成新的一代个体。例如，两条全1 和全0 的10位染色体，假如产生的交叉点位置为4，则执行的交叉操作如图1 所示。

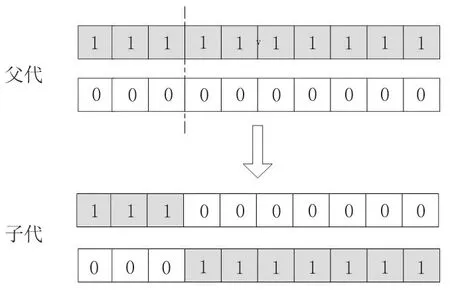
图1 交叉示意图Fig.1 Cross diagram

（3）变异。染色体在上述操作过程中可能会丢失部分基因，变异的主要目的是对其进行修补，为最优解收敛过程中的其他问题的解决提供必要的支持。一般来说变异概率的数值很小，若选择较高的变异数值，则可能会破坏最优解。

2.2 改进的遗传算法

在实际优化应用过程中，由于基本遗传算法存在一定的局部搜索缺陷，容易过早收敛而陷入局部极小区域。模拟退火算法可以根据一定概率移动而有效地跳出局部极值区域，使其越来越趋于稳定，能够进一步随机搜索寻找出符合目标函数的个体。因此，为了提高算法运行效率，及避免过早陷入局部极值，在遗传算法的基础上融合模拟退火算法，按照轮盘赌选择策略，从全体解中选择最佳个体代替最差个体，从而保证下一代个体更加适应环境。利用模拟退火罚函数来转化约束条件，改进算法的运行效率。

适应度函数与目标函数有关，在构造适应度函数时，遗传算法进行选择判断的标准是适应度较高的染色体被选中的概率大，使得下一代中一定包含最优个体，以便进入新一轮的循环计算。本文利用模拟退火算法将有约束问题变成无约束问题，其中模拟退火惩罚函数的优点在于罚因子会随着温度降低迭代的进行逐渐变大，通过罚函数将不满足约束条件的解转化为可行解，从而增大了解的搜索区域，以便快速地找到近似最优解[11-12]。

构造适应度函数为

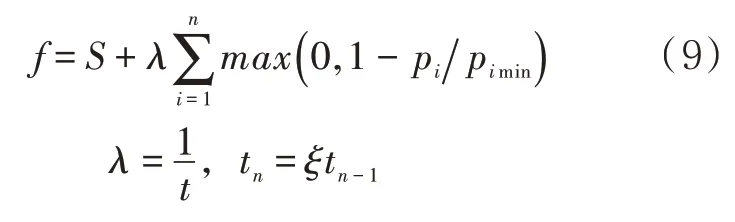
式中：λ为模拟退火惩罚因子；t为模拟退火温度，计算时需给定初始温度t0；ξ为温度冷却系数，一般在0～1 之间取值。

遗传算法求解的是最小化优化问题，而实际反应个体生存能力的适应度函数是以最大化形式表示，因此需要将上述最小值问题转化为求解最大值，此时构造适应度函数为

2.3 管径编码方法

很多经典的遗传算法通常采用二进制编码，但考虑到在天然气管网系统优化中采用的是标准管径，并且是离散的变量，故本文采用整数编码对其进行编码。该编码方式能缩短染色体的编码长度，使得计算更加简单快捷，无需反复解码，且求出的管径即为标准管径，不需要进行调整，提高了算法的实用性[1]。在相同管材的情况下，根据给定的标准管径数量设计一组一维数组，数值与标准管径从小到大分别相对应，如决策变量D=(D1,D2,…,DN)对应的染色体编码为X=(x1,x2,…,xN)，映射的整数编码如表1 所示。

表1 管径编码Tab.1 Pipe diameter codes

2.4 确定初温及退温操作

根据适应度函数，利用初始种群的相对性能来确定初温[11-12]，令

式中：Fsmin为设定的初始种群中适应度函数最小值；Fsmax为适应度函数最大值；pt∈(0,1)。

退温函数选用

2.5 算法步骤

利用改进的遗传算法来计算模型的最优解，其基本流程为：先将所需优化管线中各管径进行整数编码处理，在约束范围内随机生成一组初始种群，利用模拟退火算法对不满足约束条件的解通过罚函数变成可行解，在目标函数最优值迭代中，高温状态下的遗传算法可以搜索更大范围的解空间，随着温度的下降，遗传算法有利于改进趋于局部小范围搜索。然后判断个体是否与收敛准则相符，如不满足条件，则这些个体重新进入新一轮的选择、交叉、变异等方式迭代操作运算，直到找到最优解。

该模型具体程序流程如图2 所示。

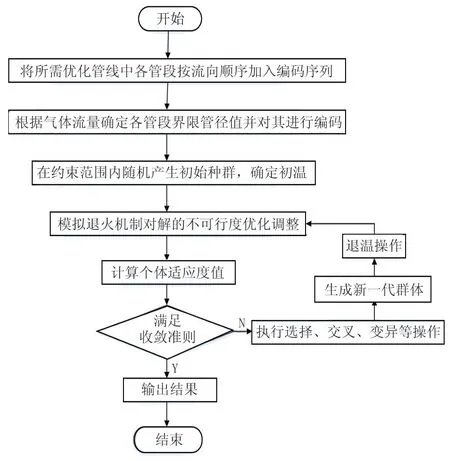
图2 程序流程Fig.2 Program flow

3 应用实例分析

选取由36 个节点和36 条管道组成的某大型天然气管网（图3），管网系统中有6 个输入节点，其余节点均为流量输出。管网系统上要求各节点压力不小于2.0 MPa。根据该算例设定的部分控制参数见表2。表3 列出了该天然气管网中部分节点的参数，其中状态1 表示该节点为流量输入，状态0 为流量输出。表4 列出了该天然气管网中部分管道参数。

图3 某大型天然气管网示意图Fig.3 Schematic diagram of a large natural gas pipeline network

表2 部分参数取值设置Tab.2 Value setting of partial parameters

表3 部分节点参数Tab.3 Partial node parameters

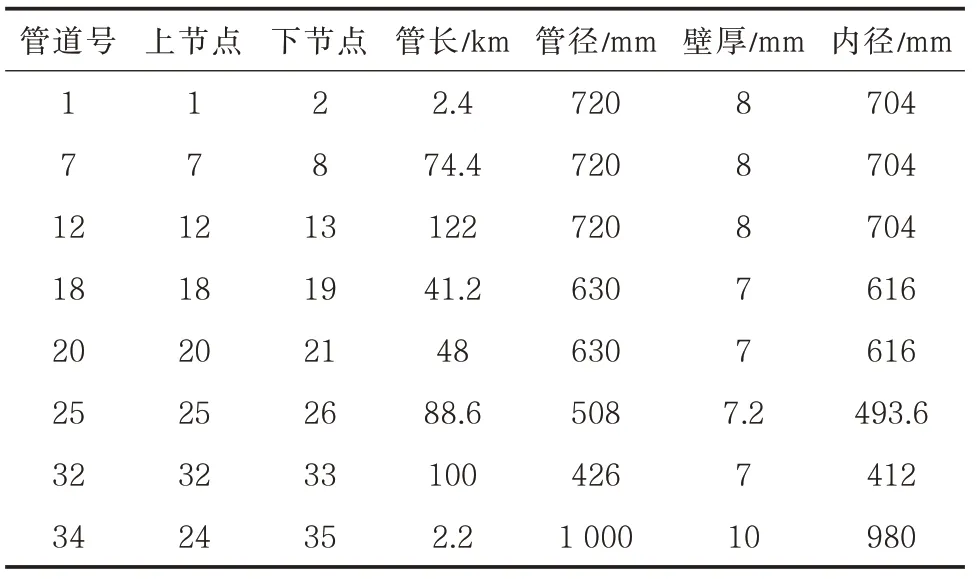
表4 部分管道参数Tab.4 Partial pipeline parameters

利用上述数学模型进行优化求解，计算了对该天然气管网运行采用基本遗传算法和改进的遗传算法得到的流量结果，表5 列出了这两种算法的部分节点结果对比。

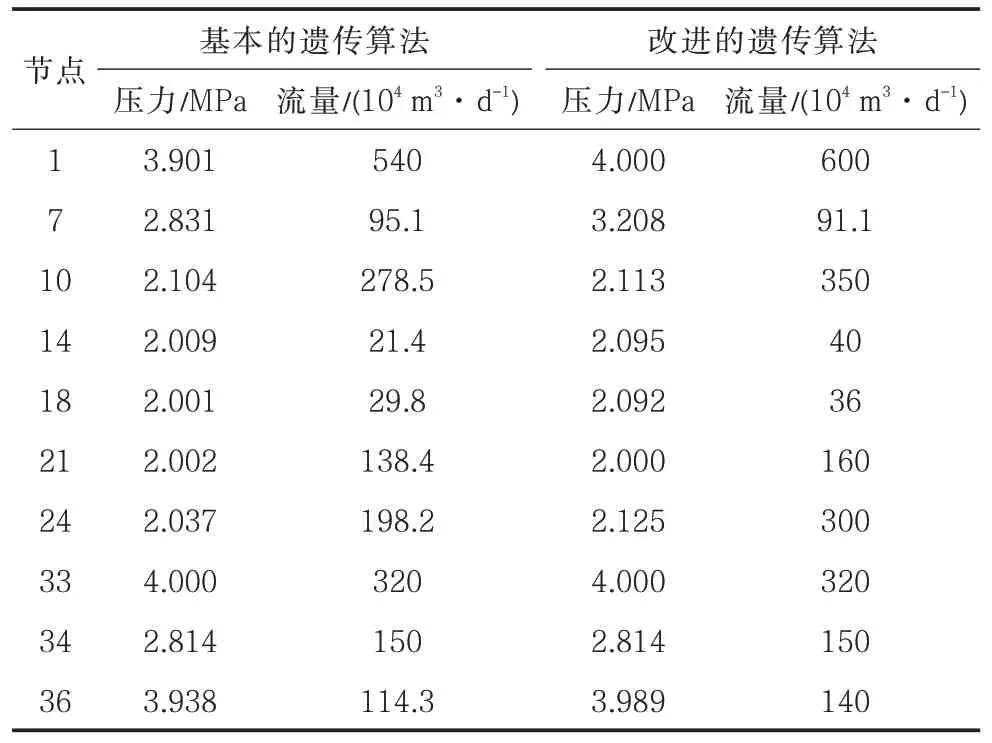
表5 部分节点计算结果Tab.5 Optimization result of partial node

从给出的部分节点流量优化数据可以看出，在压力不超过4.0 MPa 的情况下，节点1、10、14、21、24 和36 的流量在改进的遗传算法中达到了最大流量；节点33 和34 的流量在两种算法中得到的结果一致，说明均能达到最优；而节点7 的流量在基本遗传算法中得到的结果略好；对比两种算法结果说明，改进的遗传算法的优化流量结果普遍好于基本遗传算法，达到了提升天然气管网运行效率的目的。

4 结束语

（1）在天然气管网系统运行优化模型计算中，遗传算法具有较强的全局寻优能力，可以快速地在整个解空间中搜索出全体解，但在实际优化应用过程中，该算法容易达到局部最优，而模拟退火算法可以有效避免陷入局部极值现象，因此本文将这两种算法进行有效的结合，从而提高了遗传算法的全局和局部意义下的寻优效率。

（2）在保证天然气管网系统安全稳定运行的基础上，利用改进的遗传算法来求解其优化模型，某大型天然气管网的实例计算结果表明，改进的遗传算法的优化流量结果普遍好于基本遗传算法，改进的算法是切实可行、有效的，可为今后的天然气管网系统优化运行提供一定的生产指导。

（3）从该天然气管网案例来看，在实际应用中，应根据实际情况合理地选择目标函数来构建模型，要在最大限度上避免天然气事故的发生。在本文中的目标函数是天然气最大流量，没有考虑到压缩机等其他因素对天然气管道的影响，因此在今后的研究中，可将更多因素考虑进来。