以云计算资源为基础实现粒子群算法的优化

文/张乐

在多目标有可能出现冲突的情况下，要想能够实现多面综合的优化，就实现了云计算资源下动态调度管理，之后实现粒子群算法改进及RBF神经网络的设计，全面考虑虚拟机性能、应用性能、用户服务质量。通过实验结果表示，本文所研究的算法和传统算法相比，其能够实现多目标的优化。

1 云计算资源中动态调度管理机制

在通信及计算机网络中，服务主要包括区分服务和集成服务。区分服务的主要目的就是结节网络中服务质量问题，利用此概念，将其含义扩展到一不同服务等级协议实现用户服务质量的区分。那么就利用以下场景，实现以HDFS为基础的云计算动态调度管理机制。

2 基于云计算资源的粒子群算法及RBF神经网络

2.1 RBF神经网络

RBF神经网络属于三层前馈神经网络，图3为RBF神经网络的架构，其主要思想就是使径向基函数成为隐单元基，创建隐含层空间，从而实现输入矢量变换，将低维模式输入数据到高维空间中转换，从而实现低维空间中线性不可分问题能够在高维空间中变得可分。RBF神经网络主要包括隐含层、输入层及输出层，各层节点数量分别为h、n、m，输入向量表示为X=[x1，x2，...，xn]T。其中网络中的隐含层输出值得就是径向基函数输出，其主要根据输入矢量和径向基函数中心距离实现，径向基函数使用高斯函数，公式为：

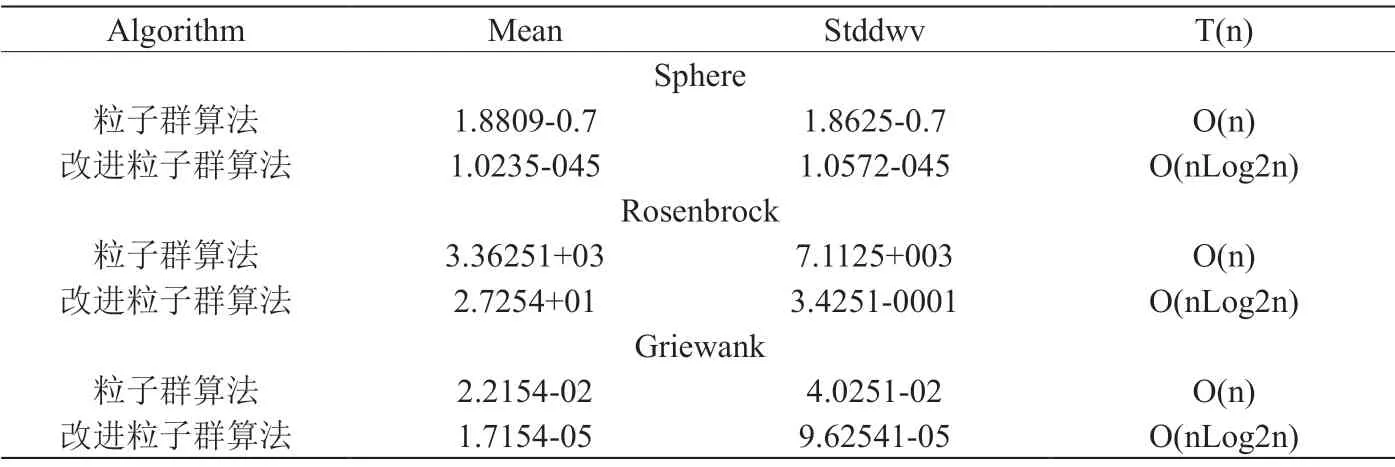
表2：对比结果

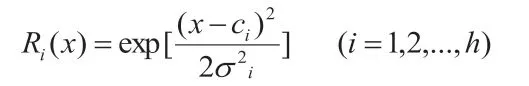
输出层的主要目的就是调整线性权值，使用线性优化策略，所以其学习速度比较快，使输出为F（Xi）， 那么：

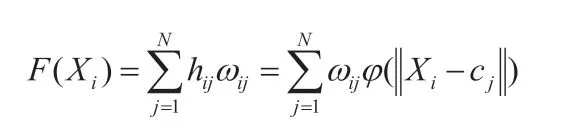
2.2 改进的粒子群算法

一个粒子群主要包括m个例子构成，其中每个例子位置都表示优化维搜索空间中的解，例子在对自身状态更新的过程中要保持自身惯性，并且要根据群体最优位置对状态进行改变。一般粒子群优化算法的数学描述都是假如在n维搜索空间中，通过m例子创建种群x=（x1，x2，...，xn）T，那么i个粒子的位置就 是xi=（xi，1，xi，2，...，xi，n）T，种 群 全 局极值表示Pg（Pg，1，Pg，n，...Pg，n，），在粒子寻找上述值之后，就能够通过以下公式对自身位置及速度进行更新。

2.3 引入惯性权重因子

为了能够使粒子群算法计算精度及收敛速度进一步的改进，可以将惯性权重因子引入到粒子群算法公式中，成为以下公式：

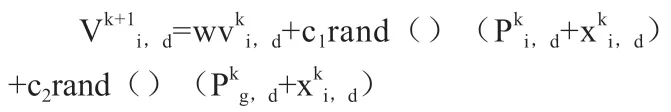
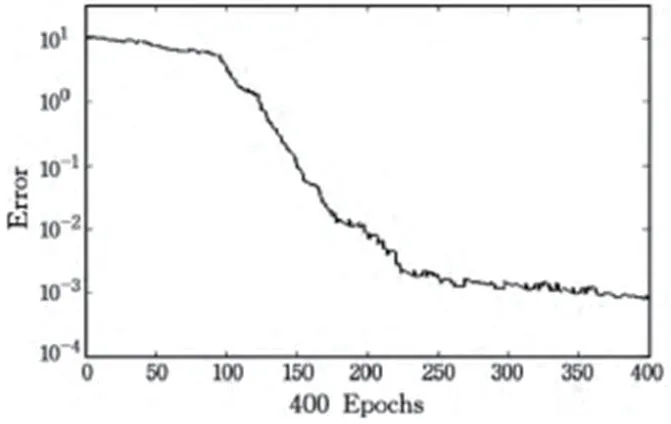
图1：RBF神经网络的收敛参数

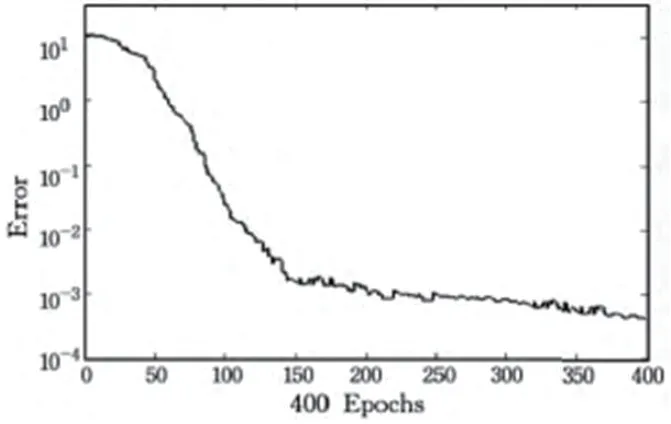
图2：优化之后的收敛曲线

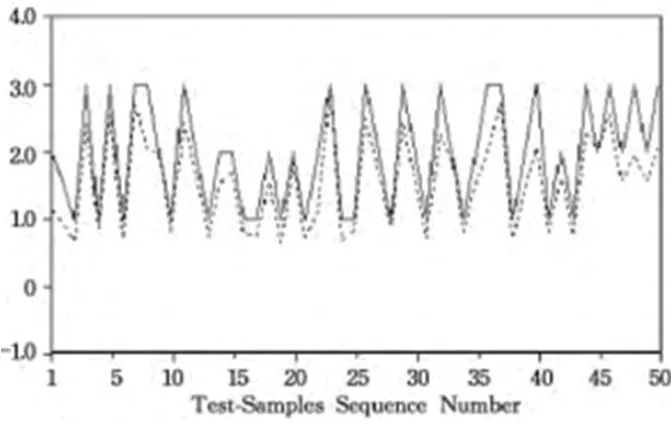
图3：网络输出和目标值的对比

其中的w值表示POS算法搜索的步长，如果w值较大，那么就能够促进跳出局部极小点，从而实现全部寻优。如果w值较小，能够促进局部寻优，促进算法的收敛。为了方便，本文将w从0.9减少到0.4的时候，此算法就是标准的PSO算法，为了能够降低计算量，使搜索方向启发性得到进一步的提高，那么就实现以目标函数为基础的关心权重因子动态调整的方法，w的变化为：

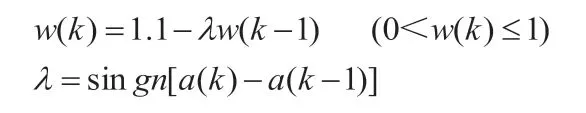
2.4 基于粒子群实现多目标优化

改进粒子群算法是以鱼群、鸟群的模拟为基础，利用个体之间的相互协助，能够实现个体与全局的最优信息进行记忆，种群中的每个例子就表示等待优化目标问题的可能解。本文根据粒子群算法操作及实现较为简单的特点，实现RBF神经网络参数与连接权重优化，并且在优化之后实现RBF神经网络云计算应用资源需求预测，RBF神经网络的优化过程为：

（1）首先设置粒子群粒子维度空间与RBF神经网络映射参数。粒子群算法中的粒子纬度和RBF神经网络参数值相互对应。

（2）设置RBF均方误差属于粒子群算法中适应度的函数，在使串码映射作为个体表达的过程中，也能够实现网络参数优化，实现训练的优化能够得到最小均方误差连接权值。

（3）使RBF连接权值参数编码作为实数向量，并且作为种群个体进行表示之后迭代。将算法迭代的过程个体向量还原成为RBF权值，之后设置参数，并且对RBF均方误差进行计算。在误差精度为指定参数的基础上对RBF均方误差进行计算，在误差精度满足指定规定迭代数量的时候就停止。

3 算法有效性的验证

为了对改进例子群算法进行验证，使用MATLAB软件神经网络工具箱实现神经网络仿真实验。本文所收集的数据为不同云计算平台的需求量，数据一共有150个，抽取100个训练，训练三十次，从而实现样本对比。图1为RBF神经网络的收敛参数，图2为优化之后的收敛曲线，图3为网络输出和目标值的对比。通过图1，图2，图3可以看出来，改进算法能够在短时间内缩小误差，提高收敛效果。图3的实线属于目标值，虚线属于网络实际输出值，实验仿真的结果能够将此模型有效性充分的展现出来，从而作为输入实际测量数据实现参考。

并且本文还选择三种常用标准测试函数对改进算法性能进行测试，并且和粒子群算法性能进行对比，表1为测试函数的参数设置，表2为测试的结果，通过表2可以看出来，改进算法平均适应度比粒子群算法要优。