交变磁场对多晶纯铝位错密度及显微硬度的影响
2020-01-17詹同军何盛亚李永成玄伟东任忠鸣李传军
詹同军 何盛亚 李永成 玄伟东 任忠鸣 李传军
(1.省部共建高品质特殊钢冶金与制备国家重点实验室,上海 200444;2.上海市钢铁冶金新技术开发应用重点实验室,上海 200444;3.上海大学材料科学与工程学院,上海 200444)
20世纪60年代初[1-3],学者们发现磁场可以影 响 位 错 运 动 和 塑 性 变 形。1970 年,Kravchenko[4]第一次提出了磁场可以影响金属的塑性,并推导了磁场下电子对位错运动的减速作用力。然而,1987年,Al’shits等[5]发现,在没有外加应力的情况下,磁场可以驱动NaCl单晶体内的位错移动。Molotskii等[6]发现,磁场可以促进金属中位错的运动,并基于位错芯与顺磁性障碍相互作用,推导了自由位错长度随磁场强度的变化关系。李红旗等[7]首次采用透射电镜原位观察了磁场作用下Fe-Ni合金中位错的发射及运动规律。刘兆龙等[8]指出,磁场作用下,顺磁性障碍物钉扎区的位错芯发生膨胀,晶格点阵对滑移的阻力下降,位错更容易移动。王宏明等[9]发现,经脉冲磁场处理后,铝基复合材料中位错密度增加、力学性能得到改善。李传军等[10-11]发现,磁致塑性效应诱发扩散偶中位错密度增加,这为原子扩散提供了高速扩散通道,从而提高了原子的扩散速率。这些研究充分说明磁场能够影响位错运动进而改善材料的塑性。但是目前关于磁场作用下金属体系中位错密度及力学性能变化规律的研究报道较少。因此,本文研究了交变磁场对形变纯铝中位错密度及显微硬度的影响机制。
1 试验材料及方法
试验材料为多晶高纯铝(99.999%,质量分数),其化学成分如表1所示,试样尺寸为8 mm×8 mm×5 mm,初始平均晶粒尺寸为150μm。
为了消除残余应力对后续试验结果的影响,并确保试样初始位错密度的一致性,对试样进行退火处理,退火温度为400℃,退火时间为8 h。然后将试样压缩形变30%以产生一定数量的位错。再将压缩后的试样真空封装在石英管中,进行有、无交变磁场的退火处理,退火温度为200℃,退火时间为1 h,试样的顶端位于磁场强度最大的位置。交变磁场退火试验装置如图1所示。采用S型热电偶监控温度,测温精度为±1℃。

表1 多晶纯铝的化学成分(质量分数)Table 1 Chemical composition of the pure polycrystalline aluminum(mass fraction) %
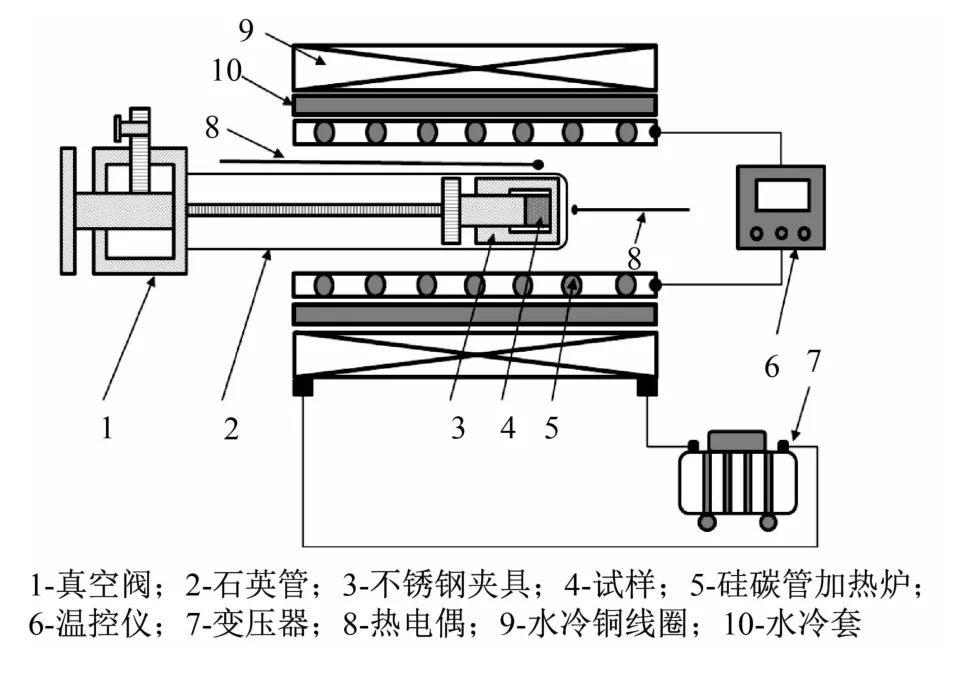
图1 交变磁场退火试验装置Fig.1 Annealing equipmentwith an alternatingmagnetic field
退火试样经打磨、机械抛光后,再进行电解抛光,工作电压为38 V,抛光时间约20 s,抛光液温度低于10℃,电解液成分是无水乙醇(72 ml)+高氯酸(8 ml)+乙二醇丁醚(20 ml)。之后依次用酒精、丙酮超声清洗试样60 s,最后保存于酒精溶液中用于随后的分析测试。
采用Bruker D8 Advance X射线衍射仪测量衍射峰的宽度,以Cu-Kα为射线源,工作电压40 kV,工作电流40 mA,扫描步长0.02°。采用粗扫(6(°)/min)和精扫(0.2(°)/min)两种扫描速率。粗扫角度(2θ)范围为10°~90°,出现了(111)、(200)、(220)和(311)晶面的特征衍射峰;对特定的衍射峰进行精扫以获得准确的衍射峰半高宽(full width at half maximum,FWHM)。最后使用MH-3L型硬度计测量显微硬度,试验力300 g(2.94 N),保载时间15 s,每个试样测量8点,取平均值。
2 结果与讨论
2.1 交变磁场磁感应强度对纯铝位错密度的影响
图2是不同强度交变磁场下退火的多晶纯铝试样的XRD谱图和(200)晶面的衍射峰。从图2(a)可以看出,有、无交变磁场处理的纯铝的衍射峰位置一致,其中(200)晶面衍射峰的半高宽则随磁感应强度的增加而变宽(图2(b))。
用Jade 5.0软件进一步获取衍射峰的半高宽数据,如图3所示。对比发现,(200)晶面衍射峰的半高宽随磁感应强度的增加而增大。
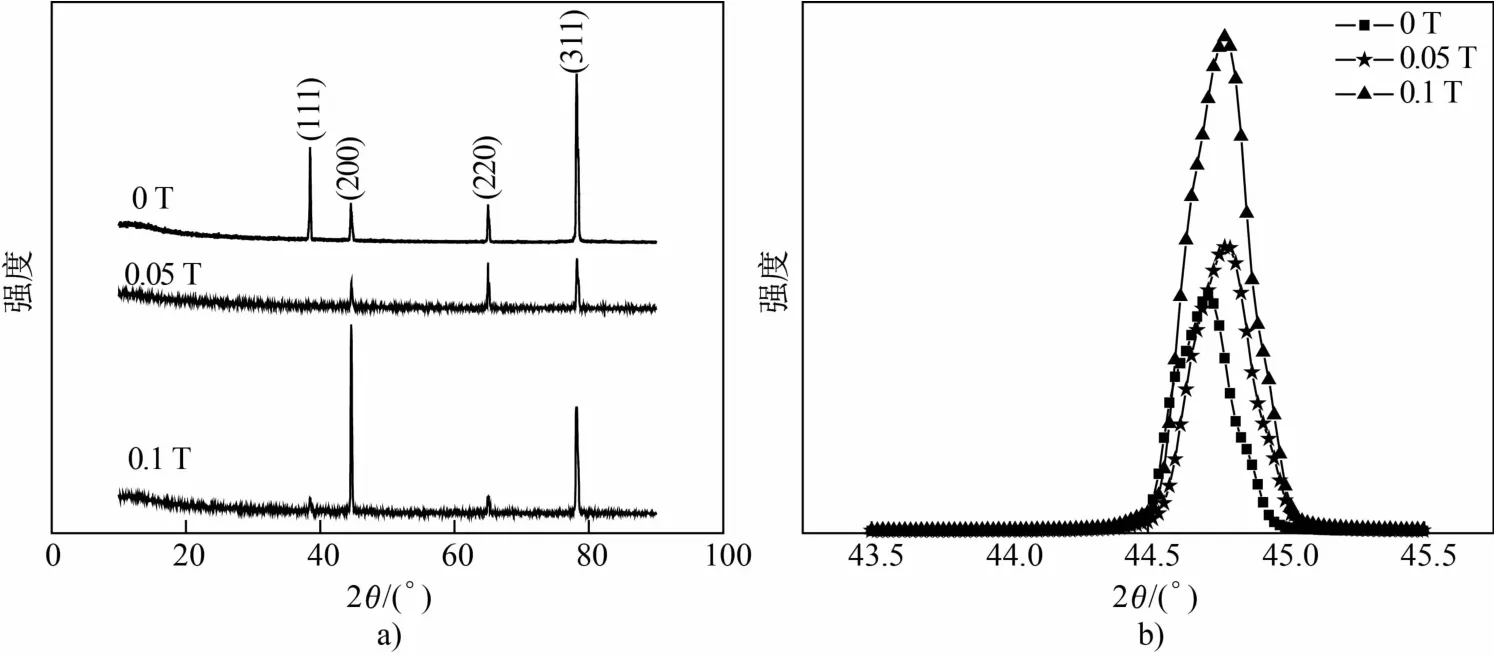
图2 有、无交变磁场退火的多晶纯铝试样的XRD谱图(a)和(200)晶面衍射峰(b)Fig.2 XRD patterns(a)and(200)diffraction peaks(b)of pure polycrystalline aluminum samples annealed with and without alternatingmagnetic field
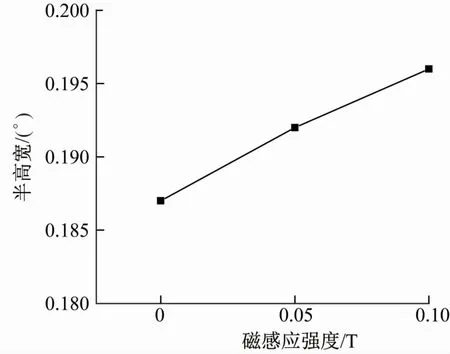
图3 有、无交变磁场退火的多晶纯铝(200)晶面衍射峰的半高宽Fig.3 FWHM of(200)diffraction peaks of pure polycrystalline aluminum annealed with and without alternatingmagnetic field
为了定量地表征位错密度随交变磁场强度变化的规律,由半高宽β可计算出试样内位错密度ρ,计算 Dunn公式[12-14]:

式中b是位错的柏格斯矢量,纯铝的柏氏矢量为0.286 nm[15]。由式(1)可知,位错密度与衍射峰半高宽的平方成正比。图4是纯铝试样(200)晶面位错密度随交变磁场磁感应强度的变化。与无磁场退火的相比,相同退火条件下施加0.05和0.1 T磁场后,试样的位错密度分别增加了5.4%和9.9%。因此,不同磁场条件下退火后试样的位错密度随交变磁场磁感应强度的增加而增大。该现象与其他合金体系经交变磁场处理后的试验结果一致[10-11]。
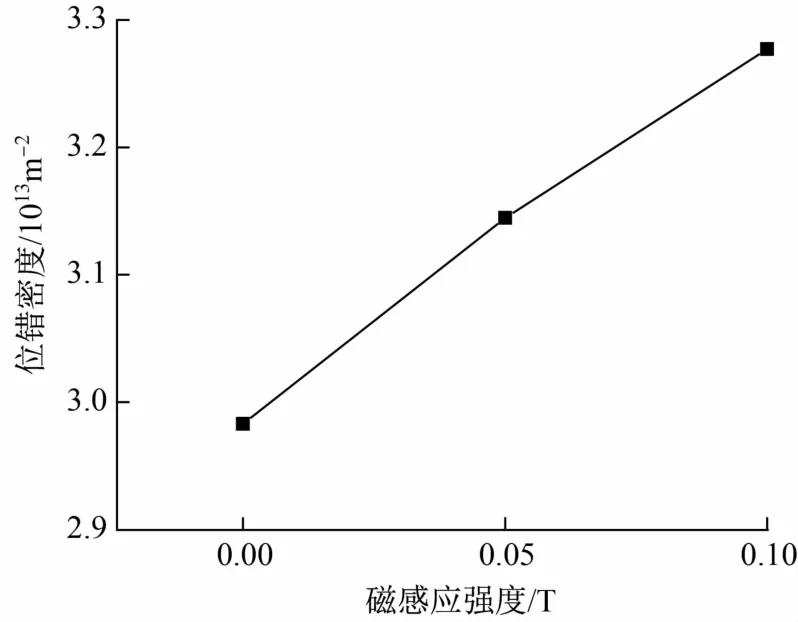
图4 纯铝试样位错密度随磁感应强度的变化Fig.4 Variation of dislocation density in pure aluminum with magnetic field intensity
以上试验结果表明,交变磁场诱发了位错的增殖。首先,交变磁场会对金属产生磁压强。根据法拉第电磁感应定律,交变磁场作用下纯铝中会产生感应电流,交变磁场与其作用产生的洛伦兹力会对试样产生一定的磁压强 P,其大小为[16]:
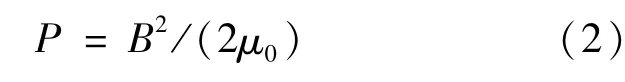
式中μ0是真空磁导率,取值4π×10-7H/m。当B=0.1 T时,P=0.04 MPa,该值远低于纯铝中位错开动的临界切应力0.79 MPa[15],更达不到材料的屈服强度。因此,磁压强并不会导致材料中位错密度大幅度增加。
此外,磁场对位错自身也会产生作用。文献[8]指出,通过Peierls-Nabarro模型可计算位错芯的半宽度。未施加交变磁场时,位错芯的半宽度为[8]:
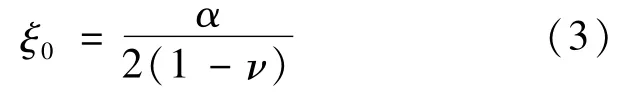
式中:α为滑移面的面间距,0<α<1;ν为材料的泊松比,铝的泊松比为0.33。当施加交变磁场后,位错芯的半宽度变为[8]:

式中η为系数,该系数既受交变磁场切向分量的影响,也和顺磁性纯铝的相对磁导率有关。

式中:H为磁场强度,r0为位错芯尺寸,h0为位错芯处磁场切向分量,G为剪切模量,μ是材料的相对磁导率。由于 μ>1,η>1,故 ξ>ξ0。
式(5)表明,随着磁场强度的增加,位错芯的半宽度增大,位错芯会膨胀。取μ=1+2.07×10-5,G=25 GPa,位错芯尺寸 r0为一个原子间距,当磁感应强度B=0.1 T时,将数据代入式(5)计算可得η=1+7.8×10-6,即位错芯的半宽度比无磁场时增加了0.000 78%。对于顺磁性位错芯而言,在交变磁场作用下,其膨胀幅度很小。
此时,晶格点阵对滑移的最大阻力近似地表示为[17]:
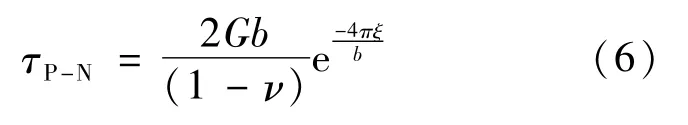
综合式(4)~式(6)可知,当交变磁场强度B=0.1 T时,钉扎阻力 τP-N比无磁场时降低了0.005%,位错滑移阻力降低幅度很小。因此,交变磁场下顺磁性位错芯的膨胀效应并不是位错密度增加的主要原因。
此外,在交变磁场作用下,由于磁致塑性效应,形变纯铝试样中的位错密度发生变化。基于Molotskii等的理论解释[6]:顺磁性障碍物与位错芯之间的强键合作用通常仅存在于电子自旋反平行的基态单重态(S态)。在磁场作用下,键合作用转变为平行自旋的三重态(T态),键合作用减弱甚至消失。因此,位错更容易从顺磁障碍物钉扎处逃逸,导致位错的自由段长度增加。
在弱磁场中,位错的自由段长度随磁场强度变化为[6]:

式中:LH和L0分别为有、无磁场条件下试样内位错的自由段长度,H是外加磁场强度,H0是促使位错从顺磁性障碍处退钉扎的特征磁场强度。试验测得金属的H0约为几百mT[6],这和本试验采用的磁场强度在同一数量级。由式(7)可知,施加交变磁场后,位错的自由段长度增加,且随着磁场强度的增加而增加。说明在交变磁场作用下,位错芯与障碍物之间的相互作用由低能态的单重态转变为高能态的三重态,导致位错自由段长度增加,位错更容易从钉扎处逃逸,促进位错运动增殖,导致位错密度增大。
2.2 交变磁场磁感应强度对纯铝显微硬度的影响
图5是有、无交变磁场退火的多晶纯铝试样的显微硬度。由图可知,随着磁感应强度的增加,试样的显微硬度逐步提高。

图5 有、无交变磁场退火多晶纯铝试样的显微硬度Fig.5 Microhardness of pure polycrystalline aluminum annealed with and without alternatingmagnetic field
在塑性变形过程中,流变应力τ是位错密度平方根的函数[18]:
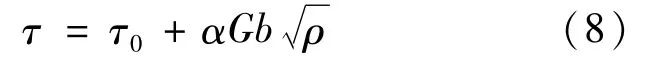
式中:τ0为无加工硬化时所需的切应力,α为与材料有关的常数,ρ为位错密度。由式(8)可知,随着材料位错密度的增加,流变应力增加,塑性变形抗力增加,硬度显著提高。
3 结论
(1)随着磁感应强度的增加,纯铝试样内位错密度增加。
(2)在交变磁场作用下,磁压强和位错芯膨胀效应对位错密度的影响不大。磁致塑性效应是位错密度变化的主要原因,该效应使位错芯与障碍物之间的相互作用由低能态的单重态转变为高能态的三重态,位错更容易从钉扎处逃逸。因此,交变磁场促进了位错的运动,导致位错密度增加。
(3)在交变磁场作用下,位错密度的增加导致纯铝试样的显微硬度显著提高。
