PMO脉冲参数对钢液内电磁场和流场分布的影响
2020-01-17秦红星刘国超徐智帅李仁兴
赵 静 秦红星 刘国超 徐智帅 李仁兴
(1.唐山学院机电工程系,河北 唐山 063000;2.上海大学先进凝固技术中心,上海 200444)
外加电磁场细化金属凝固组织的方法因其无污染、细化效果显著近年来备受关注[1-2]。脉冲磁致振荡技术(pulsed magneto-oscillation,简称PMO)是近几年来发展起来的电磁场凝固细晶技术,该技术通过电磁效应促进固液界面和熔体表面附近形核并形成“结晶雨”,从而细化整个铸坯和铸锭的凝固组织。龚永勇等[3-4]研究发现,PMO处理可以显著细化纯铝凝固组织,且在形核阶段和晶核长大的前半段处理细化效果最佳。李博等[5]、尹振兴等[6]研究了脉冲电流峰值、脉冲频率、浇注温度等对PMO细化效果的影响。梁冬等[7]通过对PMO作用下纯铝凝固再辉过程的观测,发现PMO处理增加了形核过冷度,减小了熔体内部温度梯度。Edry等[8-10]研究了PMO对纯铝凝固组织及再辉温度的影响。前期大多采用试验方法研究了PMO对较小尺寸铸锭凝固过程及组织的影响。然而大型铸锭的凝固过程与小尺寸铸锭存在很大差异,且采用试验方法研究大铸锭的凝固过程存在着成本高、周期长、不便于观察等局限性。铸锭凝固过程热模拟方法能够有效地观测铸锭特征单元的凝固组织[11-12],但不能模拟铸锭整体流场、电磁场分布等。数值模拟技术不仅可以节省研究费用、缩短计算周期,直观地呈现铸锭的凝固过程,还能够为探讨机理和工艺开发提供参考依据,已成为研究铸锭凝固过程的一种重要手段[13-14]。Kolesnichenko等[15]采用数值模拟的方法研究了立式连续铸造过程中,熔体内部电磁力和流场的周期变化规律。Wang等[16]采用试验和数值模拟相结合的方法研究了脉冲磁场作用下镁合金熔体内的电磁场分布及晶粒细化效果。Ma等[17]对脉冲磁场作用金属熔体的电磁场、电磁力、焦耳热等分布进行了数值模拟。本文运用ANSYS软件对PMO作用下钢锭凝固过程的电磁场和流场分布进行了数值模拟,研究了脉冲参数对钢液内部磁感应强度、焦耳热和钢液流速的影响。
1 数学模型的建立
1.1 几何模型
几何模型以某钢厂18 t铸锭为原型,模拟钢锭材料为P91钢,其物性参数随温度变化的曲线如图1所示。铸型材料为铸铁。为节省计算时间和空间,将三维铸锭简化为二维模型,考虑到图形的对称性,计算选取1/2模型,建立的几何模型如图2(a)所示。整个计算区域包含钢液、铸型、线圈、硅钢片和空气5个部分。为进一步比较脉冲参数对熔体内部电磁场和流场强度的影响,取某些特定位置进行计算,取点位置如图2(b)所示。其中:①、②、③、④为液面上的点,⑤、⑥、⑦、⑧为冒口与锭身相接处的点,⑨、⑩、⑪、⑫为铸锭 1/2高度处的点。图3为①~④4个点的降温曲线。输入电流波形如图2(c)所示,其中Tw为脉冲宽度,Tr为放电周期,I0为电流峰值。
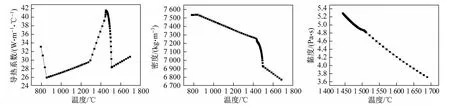
图1 P91钢的物性参数Fig.1 Thermalphysical properties of P91 steel
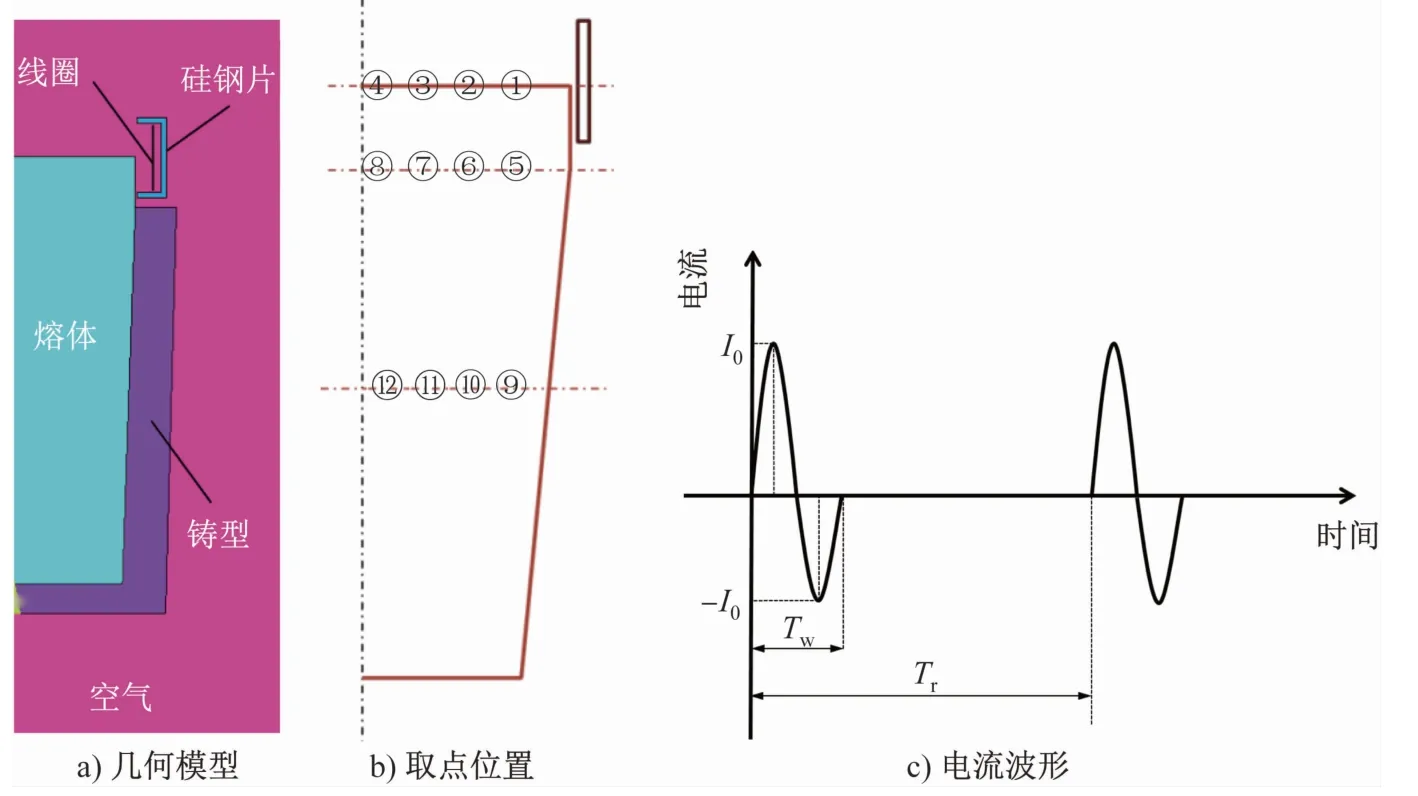
图2 几何模型及电流波形Fig.2 Geometrymodel and variation of pulsed electricity in a coil
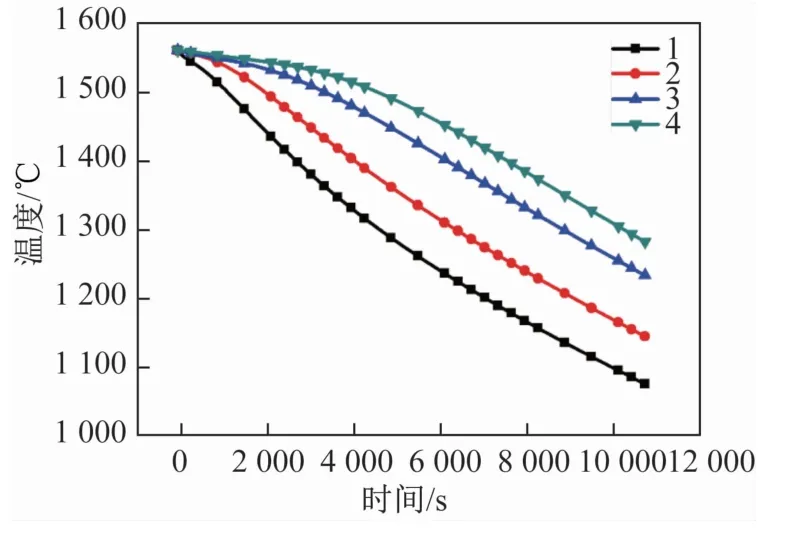
图3 液面上4个点的降温曲线Fig.3 Cooling curves of four points on the liquid level
1.2 控制方程
Maxwell方程组是研究宏观电磁问题的基础,它定量描述了电磁的相互作用和运动规律。本文模拟以Maxwell方程组作为电磁场有限元分析的依据和出发点,其微分方程如式(1)所示。脉冲电流由RLC振荡回路产生,电流随时间的变化关系如式(2)所示。
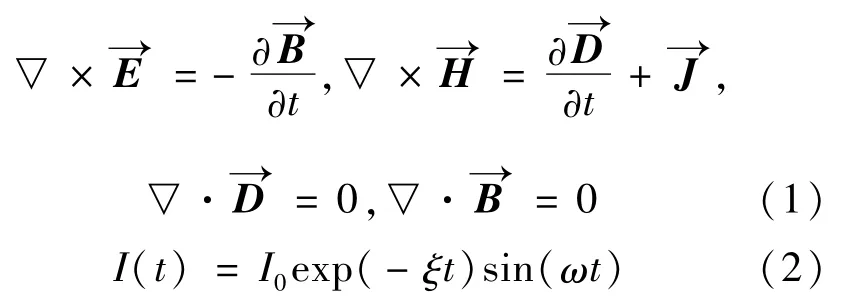
式中:E为电场强度矢量,H为磁场强度矢量,B为磁通密度矢量,D为电位移矢量,J为电流密度矢量,I0为电流峰值,ξ、ω为电流常数。
描述熔体运动的方程为连续性方程和动量方程,可以用式(3)和式(4)进行描述。
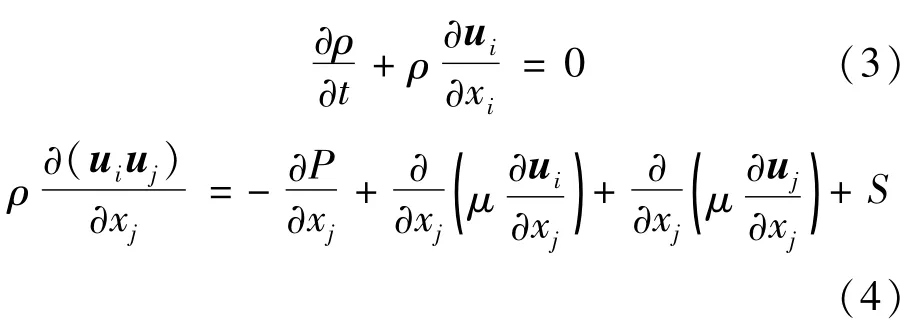
式中:ρ为钢液的密度,ui、uj为沿坐标轴方向的速度矢量,xi、xj为坐标轴的方向,P为压力,S为动量源。将电磁力F以动量源的形式加载到动量方程中进行计算,如式(5)所示:

运用 ANSYS程序中的 ANSYS/Multiphysics模块进行磁场分析,所用计算单元为PLANE13。运用FLOTRAN CFD模块进行流体计算,所用计算单元为FLUID141,其结构特征与PLANE13(电磁场计算单元)类似,从而实现电磁场与流场的耦合计算。
1.3 基本假设
(1)假设钢液为不可压缩导电流体,电导率为各向同性。
(2)只考虑电磁场对钢液流动的影响,忽略钢液流动对电磁场分布的影响。
(3)线圈周围为开放性磁场,建立铸型外侧有限空间空气域并结合无限远边界条件来模拟无限大空间。
(4)假设载流线圈具有均匀的电流密度分布,其大小由电流值、线圈截面积以及匝数来确定。
1.4 初始条件和边界条件
求解域内各个待求量 u(B、H、E、AZ)或对时间的变化率在t=0时刻,满足式(6)和式(7):
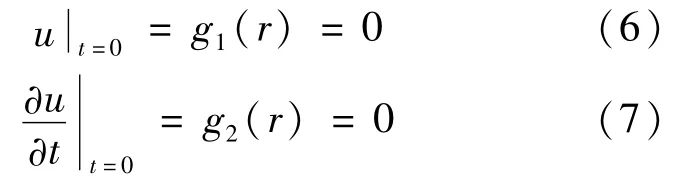
空气域外边界采用无穷远边界条件,即AZ=0。不同介质交界面条件在ANSYS软件计算中默认自动满足。
2 数值模拟结果
2.1 脉冲宽度对钢液内磁场和流场分布的影响
2.1.1 脉冲宽度对电磁场分布的影响
由于电磁场的传播特性,PMO作用下金属熔体内部的电磁场强度随时间和空间不断变化。图4为电流峰值I0=100kiA、脉冲宽度Tw=24kws(ki、kw为试验系数)时一个放电周期内磁感应强度分布情况。可以看出,受趋肤效应的影响,靠近PMO线圈的区域磁感应强度较大,熔体内部磁感应强度较小。根据δ可知,脉冲宽度越大,频率越小的电磁场的穿透深度越大。图5为相同脉冲电流峰值、不同脉冲宽度条件下Tw/4时刻熔体内部的磁感应强度分布情况。可以看出,脉冲宽度对熔体内部磁感应强度的最大值没有影响,但随着脉冲宽度的增大,磁场作用区域不断扩大。
图6为不同脉冲宽度下熔体内部不同位置处的磁感应强度。可以看出,在钢液液面①(靠近线圈型壁附近)处,脉冲宽度对磁感应强度的最大值几乎没有影响,磁感应强度的变化频率与输入电流变化频率相同。越靠近熔体内部,脉冲宽度对磁感应强度峰值大小的影响越大。脉冲宽度越大,磁感应强度越大。比较⑦和⑨点发现,Tw=48kws和 Tw=12kws时磁感应强度的最大值相差1 000倍以上。即在相同脉冲电流峰值下,脉冲宽度越大熔体内部磁场越强,离线圈位置越远,不同脉冲宽度下磁感应强度的最大值差别越大。
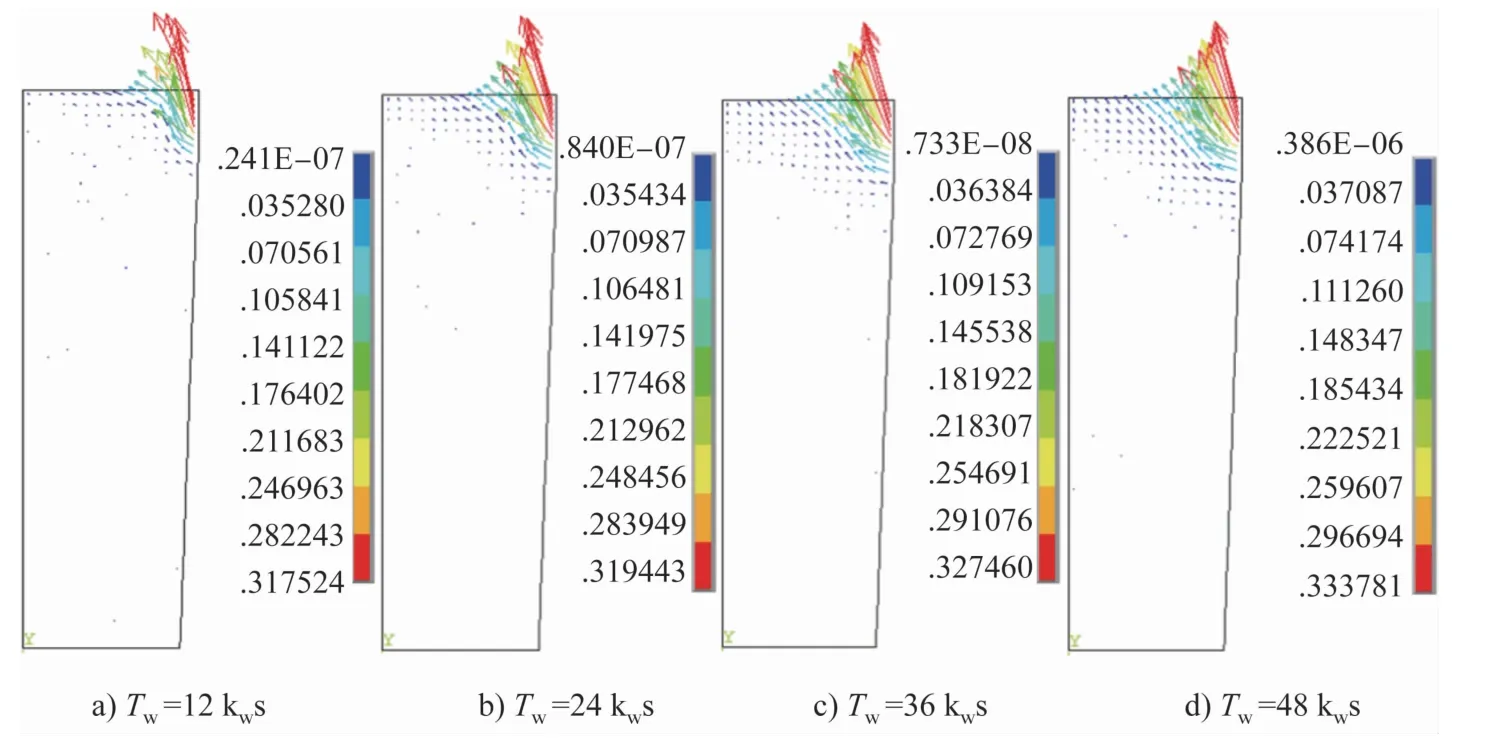
图5 不同脉冲宽度条件下T w/4时刻熔体内部磁感应强度分布(I0=100ki A)Fig.5 Distributions ofmagnetic flux intensity in melt at T w/4 with different pulse widths(I0=100kiA)
2.1.2 脉冲宽度对焦耳热分布的影响
熔体内不同位置的焦耳热随脉冲宽度的变化如图7所示。从图7可以看出,焦耳热的最大值出现在脉冲宽度最小(Tw=12kws)时,在靠近线圈①点,其值达到了7.6×107J;该位置的焦耳热随时间的变化频率与输入电流变化频率相同。在脉冲宽度以外的时间段内,焦耳热的数值接近于零。在相同时间内,脉冲宽度越小,PMO处理提供给熔体的热量越多,铸锭的凝固时间则越长,可为晶粒细化提供更多机会。在⑤、⑦、⑨点,其焦耳热的峰值随脉冲宽度的变化规律与①点有所不同,脉冲宽度越大时,焦耳热的峰值越大。脉冲宽度较小时,趋肤深度小,因此靠近熔体内部焦耳热的数值较小。
2.1.3 脉冲宽度对流场分布的影响
图8为降温100、400、800、1200s内钢液的流动情况。可以看出,降温1 200 s内冒口处钢液一直保持着剧烈的流动。但是随着冷却过程的进行,铸锭下部的流动发生了一定变化,由于铸锭各部分冷速不同导致熔体密度不同,产生了一定的自然对流,在熔体下部出现了一个很弱的回流区,与PMO引起的强制对流相比,其流速很小。
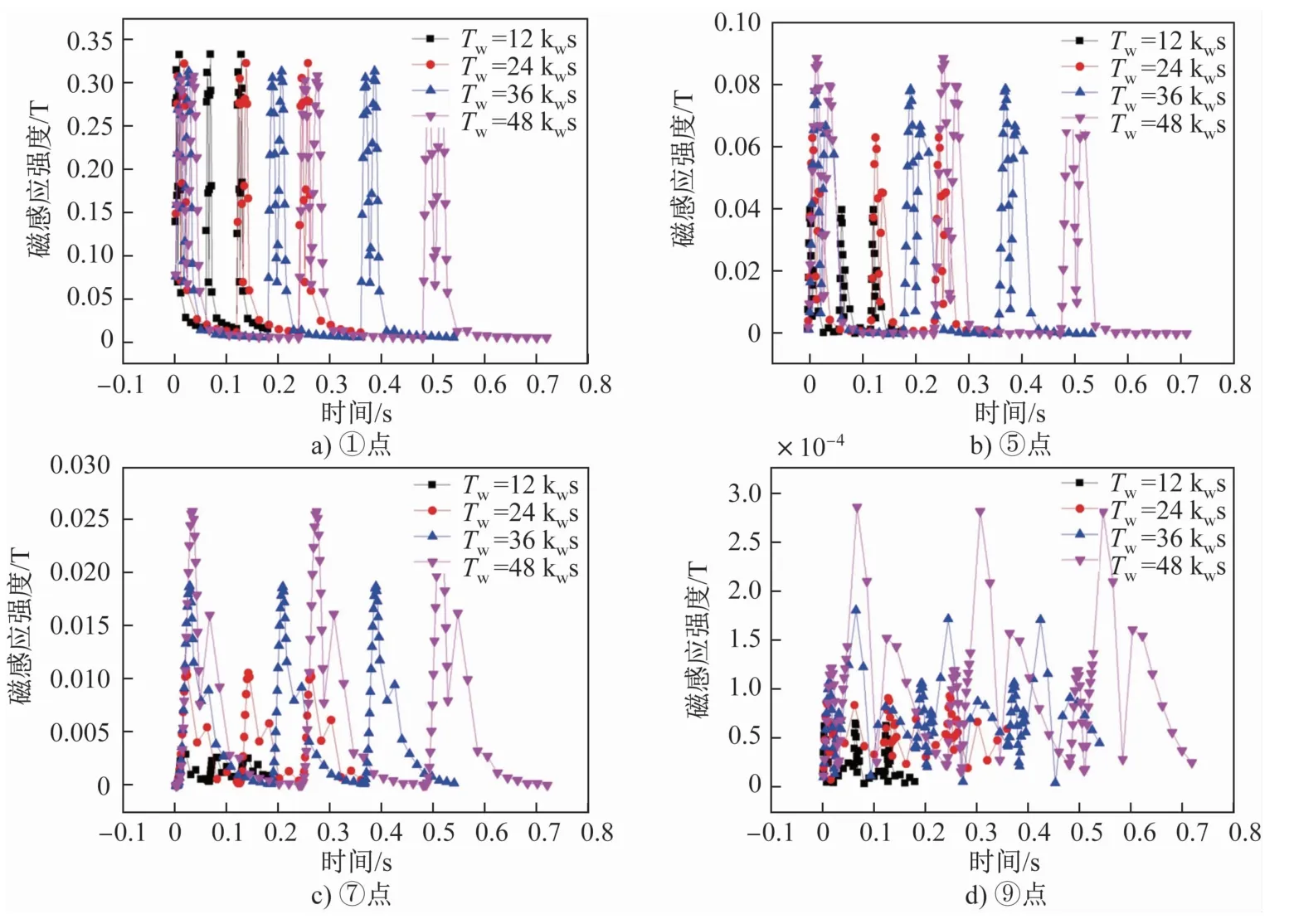
图6 脉冲宽度对熔体内不同位置磁感应强度的影响Fig.6 Effect of pulse width on themagnetic flux intensity at different positions in melt
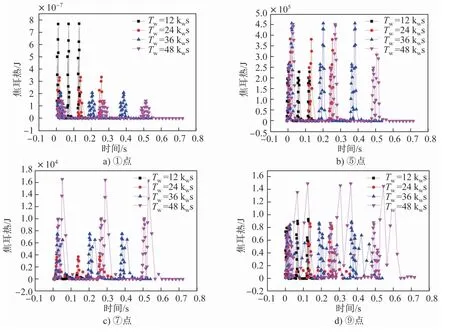
图7 脉冲宽度对熔体内不同位置焦耳热大小的影响Fig.7 Effect of pulse width on the Joule heat at different positions in melt
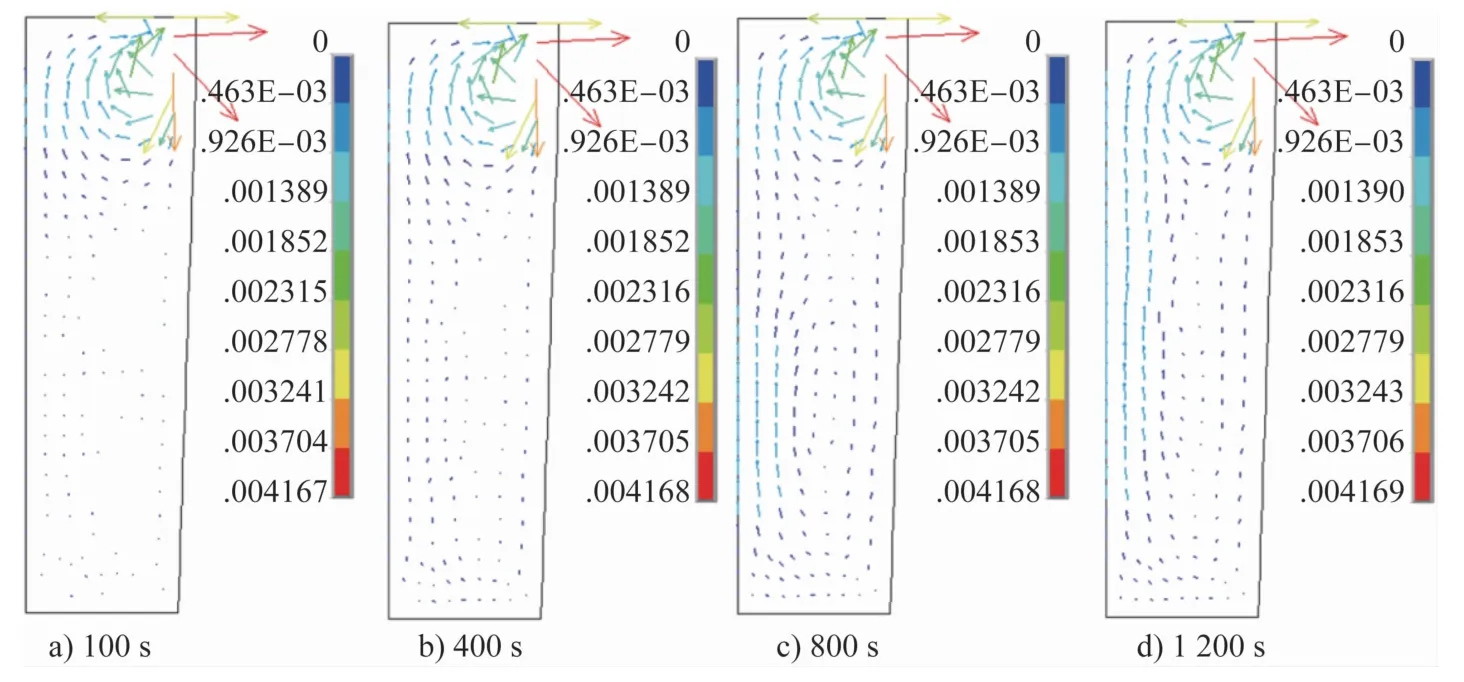
图8 不同时刻钢液流动情况(T w=24kw s)Fig.8 Distributions of fluid flow during solidification at differentmoments(T w=24kw s)
取降温400~400.3 s和800~800.3 s两段时间内①、⑤、⑨3点处的流速大小进行比较,结果如图9所示。可见,靠近线圈①点处的流速最大,铸锭1/2高度⑨点处的流速只有①点的1/200。从脉冲宽度对流速的影响来看,脉冲宽度越大,钢液流速越小,这个规律在①和⑤点比较明显,⑨点则体现不明显。⑨点处降温800 s时的流速大于400 s时的流速,这与图8中的规律一致。PMO产生的强制对流可看作是PMO产生的电磁力对金属熔体的推动作用,当脉冲宽度较大时,电磁力的变化频率较小,振荡的电磁力对金属熔体的流动作用较小,因此熔体流速小。
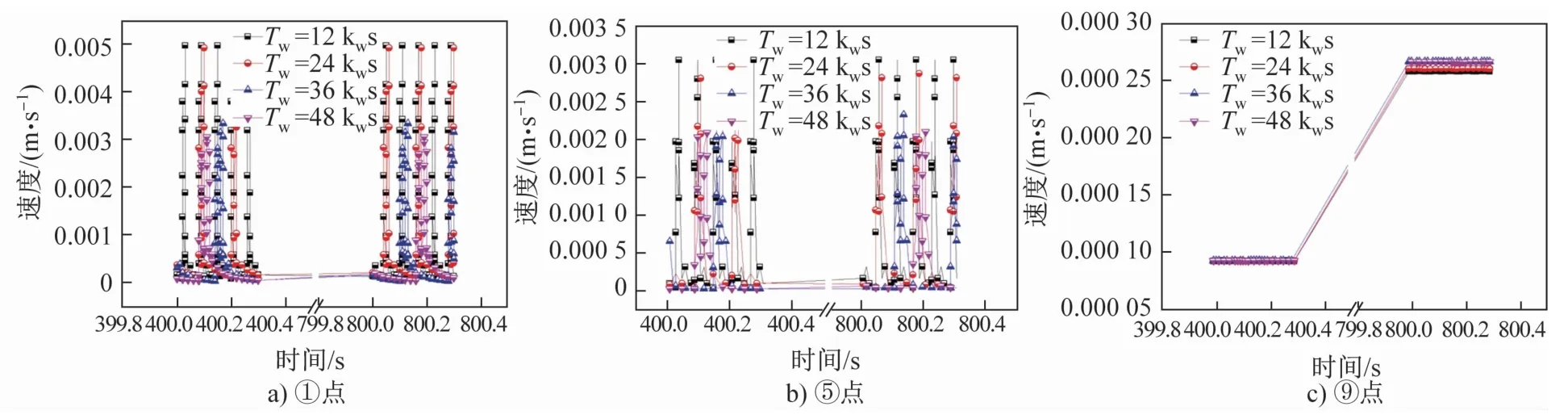
图9 脉冲宽度对钢液流速的影响Fig.9 Effect of pulse width on the flow velocity ofmelt
前期研究结果表明,PMO在金属熔体内部产生的电磁力能够促进型壁及固-液界面处晶核的脱落,脱落的晶核随熔体的流动进入熔体内部,增加了熔体内部的晶核数量,提高了形核率,从而达到了细化凝固组织的目的。在脉冲电流峰值相同的前提下,脉冲宽度的增加对电磁力的影响不大,但电磁力对熔体在单位时间内的扰动次数减少,脱落的晶核减少,因此,从这个角度考虑,应选择较小的脉冲宽度。此外,随着脉冲宽度的增加,电磁场的作用区域随之增加,当达到一定坯壳厚度时,应选择较大的脉冲宽度,增加穿透深度,否则会使固-液界面前沿晶核脱落的动力减弱。因此,综合考虑,Tw=24kw~36kws为较理想的脉冲宽度。
2.2 电流峰值对钢液磁场和流场分布的影响
2.2.1 电流峰值对电磁场分布的影响
图10为脉冲宽度Tw=24kws时,在不同电流峰值条件下t=Tw/4时刻熔体内部磁感应强度的分布情况。模拟结果显示,电流峰值对熔体内部电磁场的分布形态、作用区域的大小没有影响。电流峰值增大,磁场强度增大,磁感应强度的最大值成倍增加。图11为在3个放电周期内,①、⑤、⑦、⑨4个点处磁感应强度的大小随时间的变化。结果显示,磁感应强度的变化周期与电流峰值的大小无关,但距离线圈越远,磁感应强度的变化速度越慢。在距离线圈最近的①点,磁感应强度的变化速度与脉冲电流的变化速度基本相同。在一个放电周期内,当t<Tw时,磁感应强度随脉冲电流的变化而变化;当Tw<t<Tr时,磁感应强度几乎为0。在距离线圈较远的⑨点,磁感应强度变化不明显。此外,远离线圈位置的磁感应强度整体都很小。
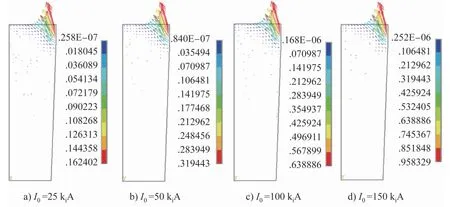
图10 不同电流峰值条件下T w/4时刻熔体内磁感应强度分布(T w=24 kw s)Fig.10 Distributions ofmagnetic flux intensity in melt at T w/4 with different peak current levels(T w=24 kw s)
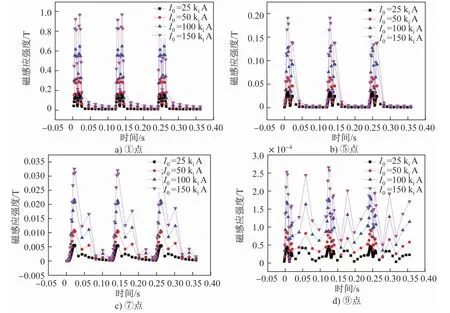
图11 电流峰值对熔体内不同位置磁感应强度大小的影响Fig.11 Effect of peak current level on themagnetic flux intensity at different positions in melt
2.2.2 电流峰值对焦耳热分布的影响
图12为电流峰值对焦耳热大小的影响。焦耳热随电流峰值变化的规律与磁感应强度相同。电流峰值越大,焦耳热的数值越大。在靠近线圈的①点和⑤点,焦耳热的变化频率与输入电流的变化频率基本相同。距离线圈越远,焦耳热的变化频率越慢。单位时间内脉冲电流峰值越大,PMO提供给熔体的热量越多。当I0=150kiA时,靠近线圈的熔体温度提高约80℃,冒口凝固时间延长,但温度过高会影响铸型及PMO装置的选材。因此,从工业应用的角度考虑,不宜选择过大的峰值电流。
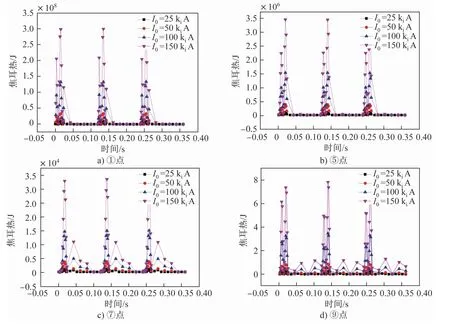
图12 电流峰值对熔体内不同位置焦耳热大小的影响Fig.12 Effect of peak current level on the Joule heat at different positions in melt
2.2.3 电流峰值对流场分布的影响
图13为电流峰值对钢液流速的影响。电流峰值对流速最大值的影响较大,电流峰值越大,流速最大值越大。在距离线圈较近的①和⑤点所受影响比较明显,总体流速较大。在距离线圈较远的⑨点降温至800 s后,出现了相反的规律,电流峰值越大,流速越小,但差别不大,推测其为与自然对流的方向相反相抵消的结果。
从凝固组织细化的角度考虑,大的电流峰值能够促使更多的晶核脱落,增加熔体内部的晶粒核心数量,从而达到细化凝固组织的目的。但是电流峰值的增加会产生大量的焦耳热,从而增加晶核重熔的可能性,促进晶核长大,对组织细化起到了相反作用。因此,综合考虑,I0=50ki~100kiA为较理想的电流峰值。
3 结论
(1)改变脉冲宽度对靠近线圈位置熔体的磁场强度影响不大,距离线圈越远,影响越大。脉冲宽度越大,熔体内部磁场越强。脉冲宽度对熔体流动的影响不大。
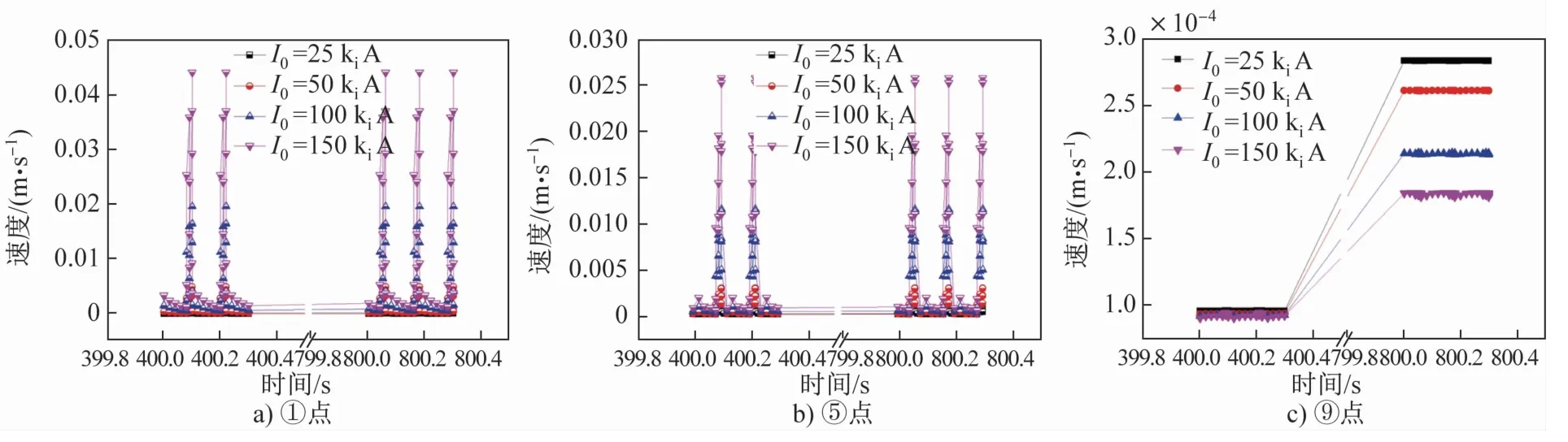
图13 电流峰值对熔体内不同位置流速的影响Fig.13 Effect of peak current level on the fluid flow at different positions in melt
(2)改变电流峰值对熔体内部磁场强度的影响较大,磁场强度和熔体的流速随着电流峰值的增加而增大。当电流峰值在25ki~150kiA范围内时,熔体内部磁感应强度的最大值在0.16~0.95 T内变化,靠近型壁处流速的最大值在0.1×10-2~4.5×10-2m/s内变化。
(3)当 Tw=24kw~36 kws,I0=50ki~100kiA时,磁感应强度、焦耳热和钢液流速均达到了一个最佳数值,铸坯可获得较理想的晶粒细化效果。
