基于变分模态分解和共振解调的轴承冲击特征
2020-01-16马建伟钱进毕建鑫
文/马建伟 钱进 毕建鑫
轴承发生早期故障时,会产生冲击振动。冲击信号是非线性,非平稳的,其故障特征常常被大量的随机噪声所淹没,所以需要对冲击信号进行研究,提取信号特征。经验模态分解(EMD)是处理非线性和非平稳信号的有效手段之一,但EMD 处理信号时有模态混叠的问题。在经验模态分解基础上提出了变分模态分解(VMD),它能够根据中心频率确定本征模态分量,从而避免了模态重叠。
小波变换(WT)分辨率比较好,能分辨出信号的时频特性,继承和提升了时频多分辨率的特点,但是小波变换只对低频信号进行分解,对于高频信号则效果不明显。共振解调是指用带通滤波和包络检波的方法将高频振动信号中的故障特征信号提取出来,并进行频谱分析的故障诊断方法。
轴承出现故障时,会产生冲击信号,对冲击信号进行VMD 分解,再进行信号重构,去除干扰信号,由于冲击信号是高频信号,所以包络解调能够将高频信号解调到低频,从而实现对轴承故障的早期诊断。
1 VMD分解
故障轴承旋转时,会产生冲击信号,VMD 的目的是把一个冲击特征信号分解为k个离散数字信号(模式),在频谱上每个模式都有有限的带宽。因此,每个模式k 需要紧凑围绕着一个中心脉动ωk,ωk是用来确定分解的。VMD 算法评估一个一维信号的带宽方法如下:
(1)对于每个模式mk,通过希尔伯特变换获得单方面频谱来计算相关的分析信号;
(2)对于各个模式,通过指数的混合调整各个估计的中心频率来转变模式的频谱基带;
(3)通过高斯方法顺利解调信号来估计带宽;例如,L2-norm 梯度的平方。然后,Dragomiretskiy & Zosso 提供了约束变分方法:
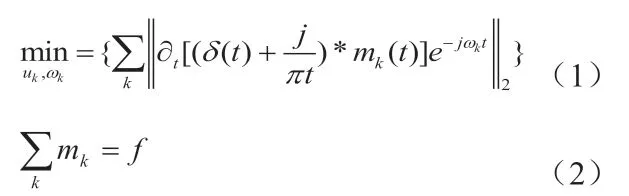
其中,f 是信号,u 是模式,ω 是频率,δ是狄拉克分布,t 是时间,k 是模式的个数,*表示卷积。伴随着高阶k 的模式u 代表低频率成分。
为求解上述约束变分问题,引入二次乘法项和 Lagrange 乘子,增广变分问题见式(3)。

运用基于对偶分解和 Lagrange 法的交替方向乘子方法求解变分问题(3),对mk、wk与β 进行交替迭代寻找最优解,见式(4)。
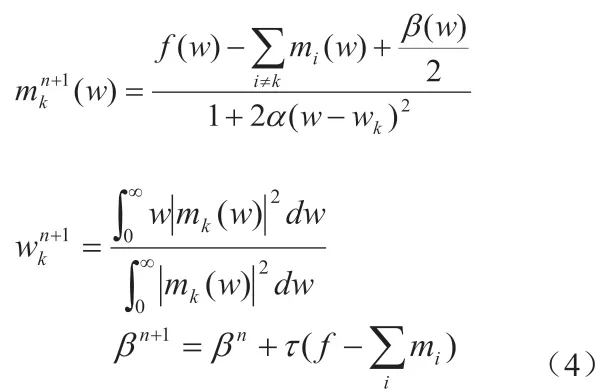
ε 是给定的,当满足下式(5)时停止迭代。最终得到模态函数mk和中心频率wk。

VMD 方法的关键在于确定模态数k,本文的模态数k 通过中心频率判断,α 采用默认值2000,τ 选为0.3,以保证实际信号分解的保真度。
2 仿真论证
深沟球轴承选用6314 型号,在solidworks建立一比一模型,设置保持架故障后导入Adams 中进行动力学仿真,故障仿真模型图如图1所示。
在Adams 中施加约束,设置转速为1800r/min,生成仿真振动数据如图2所示,对原始信号进行VMD 分解和共振解调,并进行FFT 变换,得到轴承频谱图,如图3所示。
图2是保持架出现故障情况下轴承时域图,图3是保持架出现故障情况下共振解调后的轴承频域图,轴承的主要频率是12Hz 左右,和保持架的故障特征频率一致。

图1:故障仿真模型图

图2:时域图

图3:频域图
3 实验验证
滚动轴承故障实测信号来自轴承试验台,选择有内圈故障的6314 深沟球轴承,在转速1800RPM 时轴承故障频率如表1所示,轴承试验台如图4所示,测量原始信号频谱图如图5 所示。

图4:轴承试验台
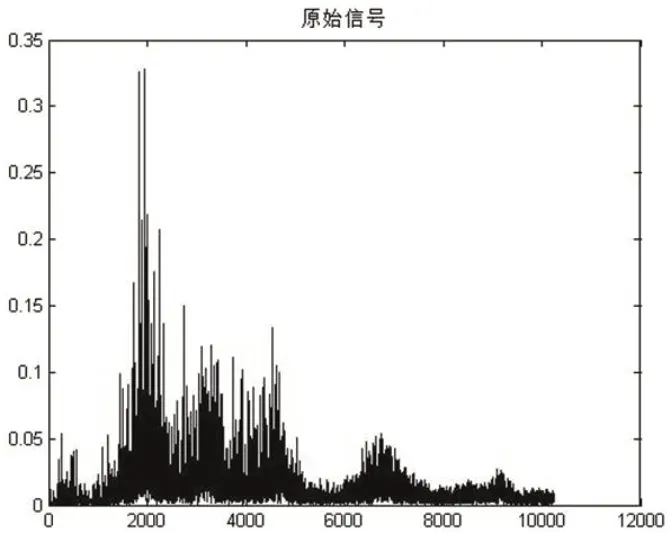
图5:轴承原信号频谱图

图6:重构信号频谱
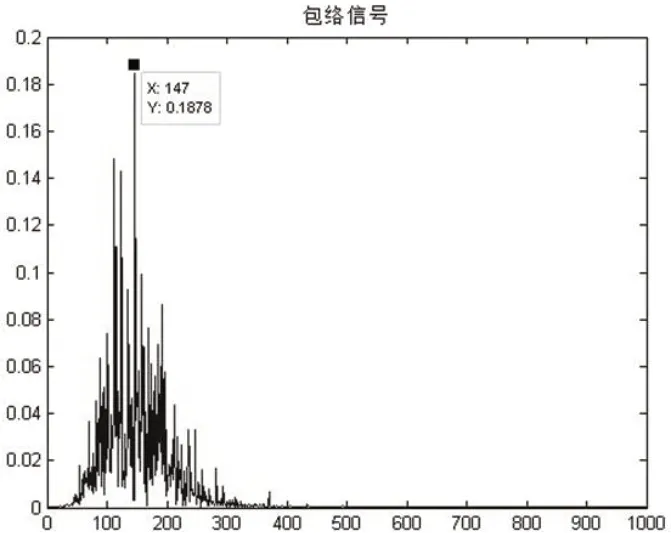
图7:包络信号解调普
对数据进行分析,设定初始本征模态函数分量层数,当K=n(n=2,3,…),对原始信号进行变分模态分解,计算出每层本征模态分量的均方差值;若出现最小均方差值,确定原始信号的分解层数为n。如果K 过大,造成计算效率低,计算负担重;若果K过小,易引入噪声,本文将K 的取值范围设为[2,16]。

表1:轴承特征频率(Hz)

表2:相关性阈值
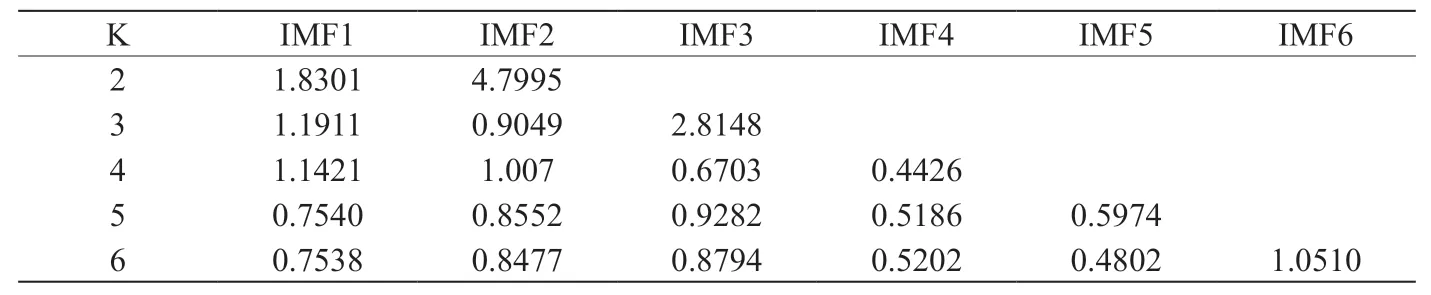
表3:VMD 分解均方差值

表4:IMF 相关系数
根据公式(9)和(10)计算原始信号和每层本征模态函数分量的相关系数ρ,

其中:X 是原始信号,Y 是重构信号。
通过相关系数ρ 进行相关本征模态函数分量的选取,如表2所示,选取相关系数ρ>0.3的本征模态函数分量进行信号重构。
对原始信号进行变分模态分解(VMD 分解),并计算出每层本征模态函数分量(IMF)的均方差值,均方差值数据如表3所示。
由表3可知,当K=4 时,IMF4 的均方差值最小,确定最优模态层数为4。选取与原始信号相关的本征模态函数分量,并进行信号重构,如表4所示。表中IMF1 和IMF2 的相关系数ρ 大于0.3,所以根据IMF1 和IMF2 对信号进行重构,重构信号频谱如图6所示。
对重构信号进行包络解调,并获得解调谱,如图7所示,提取到的特征频率为147Hz,和轴承内圈故障频率接近,说明基于变分模态分解和共振解调技术相结合的方法分析能有效的对轴承故障进行诊断。
4 结论
本文通过Adams 仿真和实验论证对轴承冲击信号的研究,可得到如下结论:
(1)Adams 仿真信号和实验信号证明了基于变分模态分解和共振解调技术相结合的方法能够识别出信号的冲击特征。
(2)基于变分模态分解和共振解调技术相结合的方法能够识别出轴承的早期故障,对保障工业生产安全起到一定的作用。
