钢筋混凝土箱梁桥弯曲抗力概率模型的确立
2020-01-16尹智昆
尹智昆
钢筋混凝土箱梁桥弯曲抗力概率模型的确立
尹智昆
(中南林业科技大学,湖南 长沙 410004)
在可靠性评估中,抗力概率模型的确立至关重要。针对钢筋混凝土箱梁桥弯曲抗力概率模型的确立,对计算模式、材料性能以及构件几何参数的不确定性进行了确立。考虑了混凝土强度的时变规律、钢筋锈蚀引起的力学性能的变化以及混凝土与钢筋粘结性能的退化,采用基于纤维模型的计算模式不确定系数,通过某钢筋混凝土箱梁桥进行了实际算例的演算,为类似的抗力概率模型的确立提供了依据。
抗力概率模型;钢筋混凝土箱梁桥;计算模式;材料性能
根据规范[1]定义:结构的可靠性是指结构在规定的时间内,在规定的条件下,完成预定功能的能力,它包括安全性、适用性和耐久性。
根据概率模型计算分析得出的结构可靠指标,则可以量化结构的可靠性大小,明确结构的安全性、适用性和耐久性程度,将其从定性转变到定量。在计算结构可靠指标的过程中,如果可以给出确定的结构抗力概率模型以及荷载概率模型,便能通过结构的功能函数计算出结构的可靠指标,以此来评估其可靠性。而本文所研究的内容即为钢筋混凝土箱梁桥的抗力概率模型的确立。
结构构件抗力是指结构构件能承受各种外加作用的能力。结构构件抗力[2]指结构构件材料的物理力学性能和其几何关系的函数。由于材料的物理性能和几何特征具有随机性,计算抗力时所采用的计算模式也具有随机性。因此,在确立结构构件的抗力概率模型之前,首先必须确立其材料性能、几何参数、计算模式的不确定性,国内外许多学者对此展开了研究:牛荻涛等人[3]给出了一般大气环境下混凝土随时间变化的时变概率模型;李广慧等人[4]在对在役结构剩余寿命预测方法的研究中给出了钢筋开始锈蚀后锈蚀深度的均值和标准差;牛荻涛[5]给出了钢筋屈服强度隧时间变化的规律;金伟良等人[6]给出了锈蚀钢筋与混凝土协同工作系数的计算模型;彭建新等人[7]在研究锈蚀RC桥梁抗力时变概率模型给出了钢筋与混凝土粘结性能衰减的计算模型;王晓明等人[8]给出了基于纤维模型的计算模式不定性的统计参数;张俊娟等人[9]给出了在役钢筋混凝土桥梁基本受力构件的抗力衰减模型。这些研究都为抗力概率模型的建立打下了基础。
本文在总结了混凝土强度、钢筋强度以及钢筋截面积损失基础上,引用了王晓明等人提出的在役梁桥弯曲抗力计算模式的不定性系数,对构件计算模式、材料性能和几何参数的不确定性进行了分析,提出了钢筋混凝土箱梁桥的弯曲抗力概率模型的确立。
1 计算模式的不确定性
结构构件计算模式的不确定性[2],指计算结构构件抗力的过程中所采用的基本假设以及计算公式的精确度不足等造成的差异性。王晓明等人给出了钢筋混凝土箱梁桥基于纤维模型的计算模式的统计参数。
规范方法和基于纤维模型的两种方法的计算模式的统计参数如表1所示。
表1 计算模式不确定性的统计参数
平均值μ/Ω标准差σ/Ω变异系数δ/Ω 规范方法1.0980.0780.071 纤维模型1.1290.0030.003
2 材料性能的不确定性
结构构件材料性能[2]指结构构件中材料的强度、弹性模量、收缩、徐变等各种物理力学性能。钢筋混凝土箱梁桥的主要材料是钢筋与混凝土。随着时间的推移,混凝土会产生碳化,钢筋会发生锈蚀,两者之间的粘结性能也会逐渐衰减,进而影响两者的共同受力。
2.1 混凝土强度的时变概率模型
一般来说,混凝土强度在初期会先随时间的变化呈上升趋势,而后会随时间慢慢下降。张建仁等人[10]对湖南省、广东省等十余座旧桥进行了混凝土强度检测,牛荻涛等人统计分析了国内外暴露试验和实测结果得出的一般大气环境下混凝土强度平均值和标准差的时变概率模型进行了修正,得到如下概率模型:
fcu()=fco×() (1)
fcu()=fco×() (2)

()=0.034 7+0.977 2 (4)
式(1)(2)中:fco,fco为混凝土28 d强度的平均值和标准差。
2.2 钢筋锈蚀
混凝土的碳化,氯离子的侵蚀均会引起钢筋锈蚀,进而导致钢筋截面积、屈服强度等多项力学性能的退化。
李广慧等人给出了钢筋开始锈蚀后钢筋锈蚀深度的平均值和标准差:

γ()=γ(0)[1+0.025(0)] (6)
式(5)(6)中:δ(0),γ(0)为0时实测到的钢筋锈蚀深度的平均值和标准差。
2.3 钢筋截面面积损失率
钢筋的锈蚀会导致钢筋截面面积的减小,由误差传递公式可以获得钢筋截面面积锈损率的平均值和标准差:

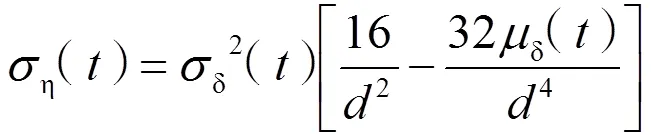
式(7)(8)中:为钢筋直径,mm。
2.4 钢筋屈服强度
钢筋锈蚀同样也会影响到钢筋的屈服强度,牛荻涛等人通过统计分析实验资料数据,给出了锈蚀钢筋屈服强度的平均值和标准差:
fs()=[1-1.077η()]fs(9)
2fs()=[1-1.077η()]2fs2+1.0772fsη2()(10)
式(9)(10)中:fs,fs分别为未腐蚀钢筋屈服强度的平均值和标准差,MPa,其值可查阅规范[11]获得。
3 几何参数的不确定性
结构构件几何参数[2]指结构构件的截面几何尺寸特征,如构件高度、宽度、截面面积等。对于已建结构,可以通过仪器直接实测出构件的几何尺寸。
4 抗力模型
对于钢筋混凝土箱梁桥,按惯性矩相等和面积相等的原则,将箱型截面转化为等效的工字形截面,判断该截面属于第几类截面,再根据等效的工字形截面建立其弯曲抗力概率模型。在计算过程中,因为结构构件抗力的计算模式,大部分为=1·2·3…或=1·2·3+4·5·6+…+n-2·n-1·n,因此在实际计算时,不论i(=1,2)怎样分布,都可以假定结构抗力遵循对数正态分布。通过此方式不仅简单易操作,并且可以达到较高的精度要求。
5 实例计算
某大跨径钢筋混凝土箱梁桥,全长976.62 m,主桥设计桥型为(65+120+65) m的连续箱梁桥,混凝土标号为C55,钢筋采用HRB335,纵向主筋采用φ16,钢筋截面积=6 033.4 mm2,箱梁横截面尺寸如图1所示。此桥已投入使用10年,经检测测得的混凝土抗压强度平均值为57.2 MPa,标准差为0.432。钢筋的平均锈蚀深度为0.02 mm,标准差为0.05。

图1 箱梁横截面
把fco=57.2,fco=0.432,=10代入式(1)~(4)可得fcu()=82.4 MPa,fcu()=0.666,再换算成轴心抗压强度,fc()=55.2 MPa,fc()=0.446。
把δ(0)=0.02 mm,δ(0)=0.02,0=10,=10,代入式(5)(6)得δ()=0.02 mm,δ()=0.02。再由式(7)(8)得到钢筋截面面积的损失率η()=0.005 0,η()= 0.000 025。
由规范查得fs=380.20 MPa,fs=21.7,将其代入式(9)(10)得fs()=378.15 MPa,fs()=21.58。
由于箱梁截面尺寸已给出,因此这里计算抗力时不考虑几何参数的不确定性。将箱型截面转化为等效的工字形截面,如图2所示,再来进行相关抗力模型的计算。
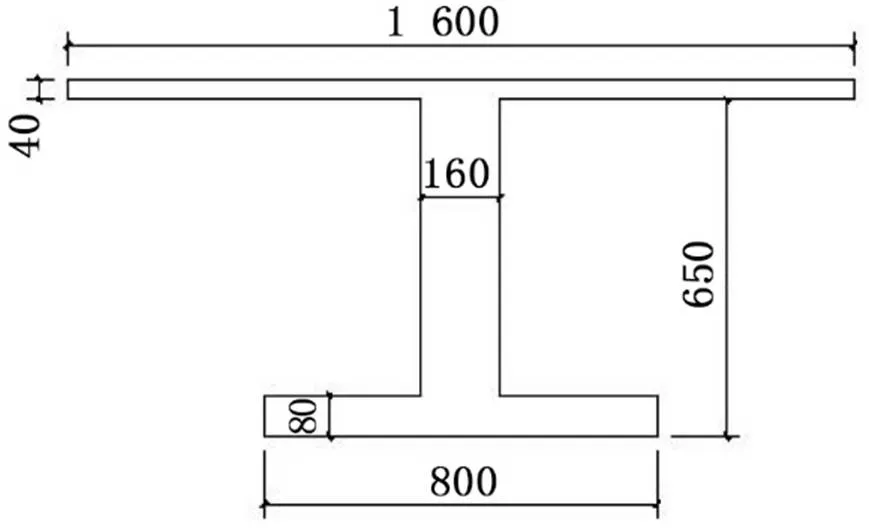
图2 工字型截面
经验算,此梁属于第一类T形截面。第一类T形截面梁抗弯承载力的抗力统计参数为:


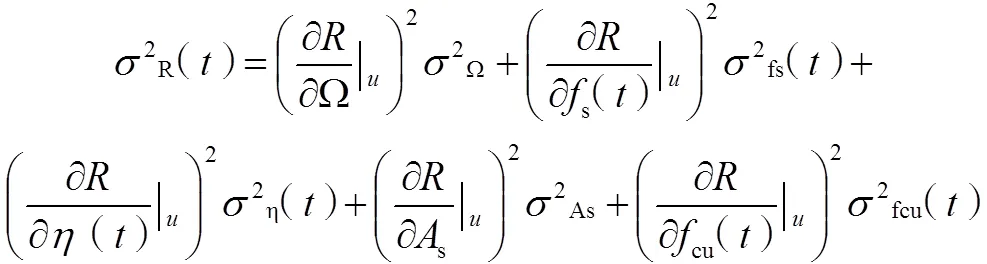
由规范[11]可知As=1.0 As,As=0.035 As,将相关数据代入式(11)(12),可以求得弯曲抗力的统计参数R()= 1 686.880 kN·m,R()=234.887。如果能确定荷载概率模型的统计参数,便可以通过可靠度计算方法计算出结构的可靠指标,进而判断出该箱梁桥在该时刻的可靠性,这也是确立抗力概率模型的目的。
6 结论
抗力模型的确立对于桥梁可靠度的评估至关重要。本文通过对钢筋混凝土箱梁桥计算模式、材料性能和几何参数不确定性的确立,将箱型截面转化为工字型截面,从而确立了连续箱梁桥的弯曲抗力概率模型,为钢筋混凝土连续箱梁桥的可靠性评估、剩余寿命的预测打下了基础。
[1]中华人民共和国建设部.GB 50068—2001 建筑结构可靠度设计统一标准[S].北京:中国建筑工业出版社,2001.
[2]张建仁,刘扬,许福友,等.结构可靠度理论及其在桥梁工程中的应用[M].北京:人民交通出版社,2003.
[3]牛荻涛,王庆霖.一般大气环境下混凝土强度经时变化模型[J].工业建筑,1995,25(6):36-38.
[4]李广慧,杜朝,蒋晓东.在役建筑结构的剩余寿命预测[J].郑州大学学报(工学版),1999,20(3):6-9.
[5]牛荻涛.混凝土结构耐久性与寿命预测[M].北京:科学出版社,2003.
[6]金伟良,赵羽习.锈蚀钢筋混凝土梁抗弯强度的试验研究[J].工业建筑,2001,31(5):9-11.
[7]彭建新,张建仁,张克波,等.锈蚀RC桥梁弯曲抗力时变概率模型与试验研究[J].工程力学,2012,29(6):125-131.
[8]王晓明,石雪飞,阮欣.在役梁桥弯曲抗力概率模型的确定方法[J].结构工程师,2013,29(4):51-55.
[9]张俊娟,穆卓辉.钢筋混凝土桥梁抗力模型的建立及应用[J].水资源与水工程学报,2015,26(5):186-191.
[10]张建仁,刘扬.混凝土桥梁构件服役期的抗力概率模型[J].长沙理工大学学报(自然科学版),2004(1):27-33.
[11]中华人民共和国交通运输部.GB/T 05283—1999 公路工程结构可靠度设计统一标准[S].北京:中国计划出版社,1999.
U441
A
10.15913/j.cnki.kjycx.2020.01.018
2095-6835(2020)01-0059-03
尹智昆(1993—),男,湖南洞口人,硕士研究生,主要研究方向为桥梁工程。
〔编辑:严丽琴〕
