PBX模拟材料压剪应力状态下的幂函数M-C强度准则与失效特性

贾 东，高 洋，陈勇梅，周燕良，郝志明，黄西成

（中国工程物理研究院总体工程研究所，四川 绵阳 621999）

1 引言

高聚物粘结炸药（PBX）是以炸药晶体颗粒为主体加上高聚物粘结剂、钝感剂等经一定工艺合成的颗粒复合材料。在武器系统中，PBX 炸药部件既是物理功能件也是力学结构件，其结构强度问题是武器工程中一个亟待解决的关键问题，所以，建立PBX 炸药材料的强度准则对于武器结构的设计和分析有着重要意义。

研究表明，PBX 在力学性能上具有明显的拉压不对称性，其失效破坏模式与其所处的应力状态息息相关，在拉伸应力状态下主要呈现出张裂破坏，在剪切、压缩以及围压状态下则主要呈现出剪切破坏［1-3］。目前，国内外关于PBX 拉伸破坏行为的研究已经很多［4-8］，但对于剪切破坏的研究还相对较少，D.A.Wiegand［9-11］等人较早开展了PBX 在单轴压缩和围压状态下的剪切破坏强度分析，并认为在低围压应力状态下Coulomb 准则是适用的；美国Los Alamos 国家实验室的Stevens［12］针对PBX 9501 的单轴拉伸和压缩实验结果，采用线性M-C 准则拟合得到了其强度包罗线。李俊玲等［13］对PBX 开展了动态压缩实验研究，发现M-C 准则对PBX 剪切破坏行为的描述与实验结果较为吻合；唐维等［14-15］采用端部约束下的圆柱压溃实验，分析了某TATB 基PBX 的失效破坏强度，认为在三向压缩状态下M-C 准则的描述精度更高，针对PBX 模拟材料开展了不同围压下的三轴压缩实验，获得了轴向压缩强度的变化规律。从已有的研究情况来看，M-C 准则是最适用于材料剪切破坏行为描述的，它能体现出剪切破坏时的压力相关性，但受限于PBX 剪切强度实验研究的匮乏，对其强度特性的认识还不够深入，且目前研究中大多采用线性M-C 准则，对材料压力相关性的描述能力有限，所以有必要开展更多的实验和理论研究。

本研究通过变角剪切加载方法，针对PBX 模拟材料开展压剪实验研究，获得其在压剪应力状态下的强度变化规律，建立PBX 模拟材料的幂函数M-C 强度准则，分析其压剪破坏的细观损伤失效特性。

2 实验设计

2.1 实验试样

本实验试样为20 mm×20 mm×20 mm 正方体试样，试样材料为PBX 模拟材料，主要采用三聚氰胺（C3N6H6）和硝酸钡（Ba（NO3）2）颗粒替代高能炸药颗粒，再配以聚合物粘结剂进行等静压成型，其材料密度约为1.8 g·cm-3。

2.2 实验装置

压剪实验是获取材料剪切破坏参数的重要方法，在岩石、混凝土等材料强度研究中已广泛应用［16-17］。为获得PBX 模拟材料剪切强度的压力相关性，设计的变角剪切加载装置将开展0°，15°，30°，45°，60°，75°以及90°共计7 种加载角度（试样剪切面与轴向载荷的夹角θ）的压剪复合加载，其中0°和90°分别代表简单剪切和单轴压缩应力状态，如图1 所示。

图1 变角剪切加载装置Fig.1 The shear loading device with variable angle

变角剪切加载装置上下压头采用反对称设计，通过压头上的角度调节孔实现不同角度的压剪复合加载；装置底部的水平滑轨可使试样在安装时与加载模块自适应接触，同时消除加载过程中对试样附加的水平方向载荷。

2.3 实验数据处理

压剪实验是通过单轴压缩载荷在试样压剪面（图1 中红色虚线）上产生压缩和剪切的复合作用，并使试样最终沿该平面发生破坏，利用矢量叠加原理可以得到正应力和剪应力的计算公式：

式中，σ为正应力，MPa；τ为剪应力，MPa；P为轴向压缩载荷，N；a为试样边长，mm。

3 幂函数M-C 准则

在剪切破坏的强度准则研究中，Coulomb［18］最早提出了破坏面上剪切强度与正应力呈线性关系的Coulomb 准则，其表达式为

式中，c为材料的粘聚力，MPa；φ为材料的内摩擦角，（°）。随后Mohr 基于应力圆的切线包罗线提出了用于描述材料失效破坏的Mohr 准则，而当包罗线为直线时，该准则与Coulomb 准则一致，即为线性Mohr-Coulomb 准则［19］，在σ-τ平面上，Mohr 圆和破坏包罗线之间的关系如图2 所示。

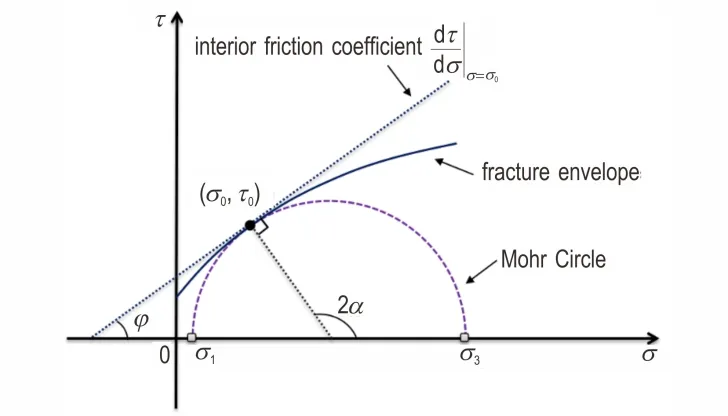
图2 正应力-剪应力平面上的破坏包络线Fig.2 The fracture envelope on σ-τ plane

在实际应用中，研究者提出了不同形式的非线性M-C 准则，主要有抛物线M-C 准则和双曲线M-C 准则［20］。由于这些准则中的拟合指数均为固定值，对拟合数据的适应性有限，所以本研究将采用一种更为普适的非线性M-C 准则—幂函数M-C 准则对PBX 模拟材料的剪切强度特性进行分析，其具体表达式为：

式中，a和b均为模型参数，MPa；m为该准则的幂指数。当m=1 时，该准则即可退化为线性M-C 准则，当m=2 时，该准则即为抛物线M-C 准则。根据图2 中破坏包罗线与主应力（以压为正）之间的关系，正应力σ和剪应力τ可以表示为：

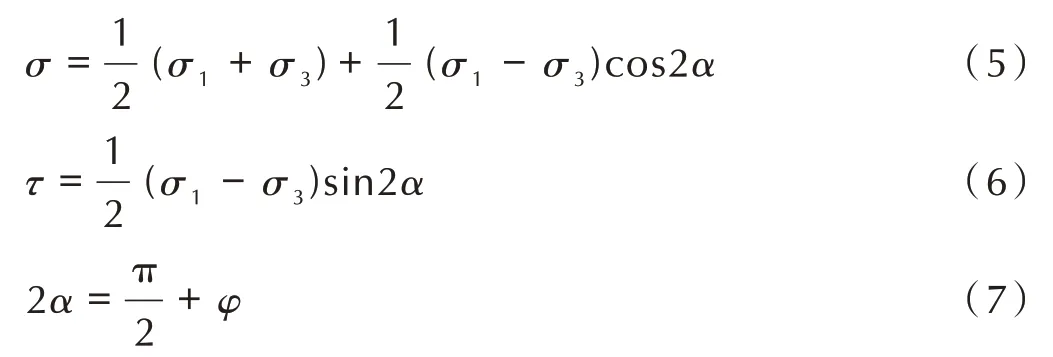
式中，σ1为第一主应力，MPa；σ3为第三主应力，MPa；α为第一主应力与剪切面的夹角，（°）。根据公式（4），幂函数M-C 准则在任一正应力σ0下的内摩擦系数k（σ0）可以描述为：

结合公式（5）～（8），可以得到σ-τ平面上任一点（σ0，τ0）对应的主应力σ1和σ3，其表达式为

式（8）～式（10）说明，当幂函数M-C 准则的参数（a、b和m）确定后，即可获得材料发生失效破坏时的第一主应力σ1和第三主应力σ3。

4 结果与讨论

4.1 压剪实验结果

按照上述实验方法，得到了PBX 模拟材料压剪试样在不同加载角度下的宏观破坏模式，如图3 所示。

图3 不同加载角度下的宏观破坏模式Fig.3 Macroscopic fracture patterns under different loading angles

从图3 可以看出，当θ为0°，15°，30°，45°时，压剪试样均沿既定剪切面发生剪切破坏，剪切断面明显；当θ为60°，75°，90°时，试样无法沿既定剪切面发生贯穿破坏，除存在剪切破坏的特征外，在与剪切面垂直的方向上还出现了局部的拉伸破坏面，整个试样呈现出剪切和张裂的混合破坏模式。根据压剪实验的宏观破坏模式可以看出，在压剪角度θ为0°，15°，30°，45°条件下获得的实验数据是有效的，可以用于描述PBX 模拟材料的剪切破坏强度，相关实验及结果如表1 所示。

从表1 的结果可以看出，不同压剪角度下的破坏载荷值分散性较小，其相对标准差CV（标准差和均值的比值）均小于10%，符合GJB 772A 对实验精密度的要求，这说明实验数据的分散性是可接受的。当θ为0°，15°，30°，45°时，随着加载角度的增加，剪切破坏面上的压应力和剪应力均逐渐增大，符合M-C 准则的变化趋势；而当θ为60°，75°，90°时，试样的破坏模式并不单一，无法计算获得其发生破坏时的真实应力状态。

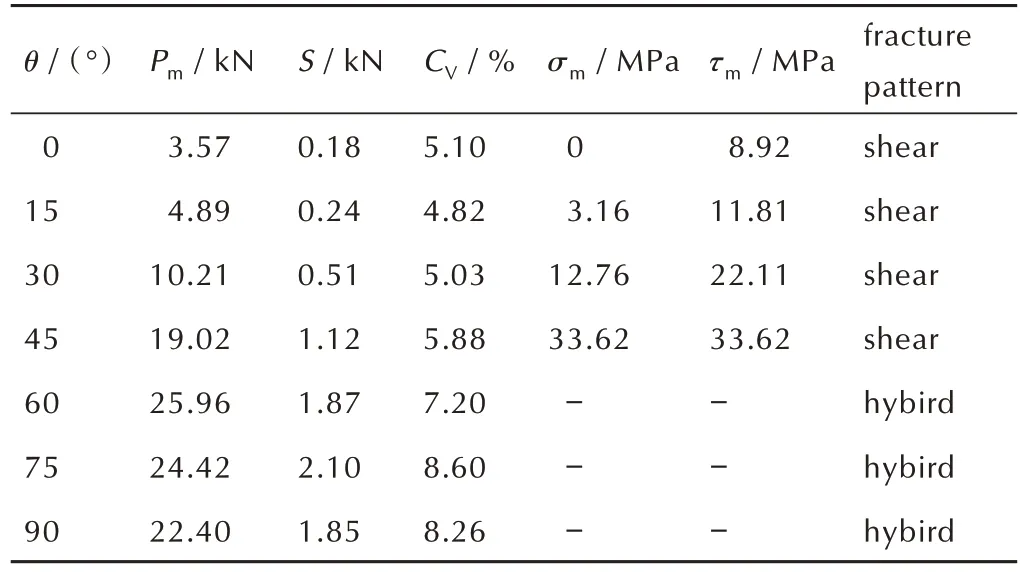
表1 压剪实验结果Table 1 Results of compression-shear test

4.2 强度准则建立与围压预测

根据压剪实验的结果，为考察幂函数M-C 准则在PBX 模拟材料剪切强度实验数据拟合方面的适用性，分别利用线性M-C 准则和幂函数M-C 准则对加载角度θ为0°，15°，30°，45°的压剪实验数据进行拟合，其拟合曲线如图4 所示。

图4 不同M-C 准则的拟合曲线Fig.4 The fitted curves of different M-C criterions

从拟合曲线可以看出，针对θ为0°，15°，30°，45°的压剪实验数据，幂函数M-C 准则的拟合相关性明显优于线性M-C 准则，更加符合PBX 模拟材料剪切强度的非线性变化趋势，具体拟合参数及相关指数如表2所示。

表2 不同M-C 准则拟合参数Table 2 Fitted parameters of different M-C criterions

为了进一步验证本研究中强度准则的适用性，利用理论计算公式（8）～（10）对PBX 模拟材料的三轴压缩强度进行预测，并与文献［15］中相同PBX 模拟材料的实验数据进行比较，具体结果如图5 所示。

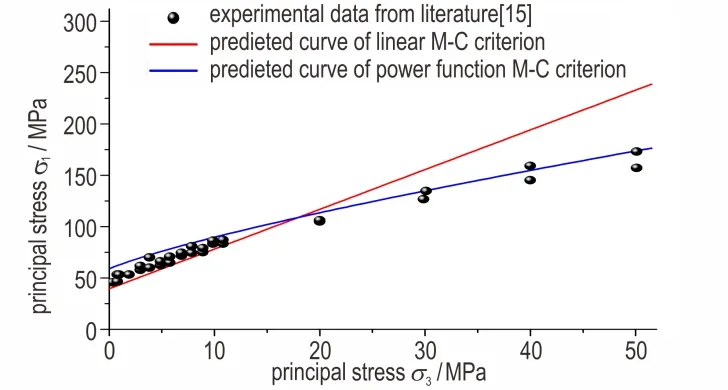
图5 三轴压缩理论预测与实验数据的比较Fig.5 Comparison of theoretical prediction and experimental data for triaxial compression

从图5 的预测结果来看，幂函数M-C 准则的预测曲线整体趋势与三轴压缩实验数据的变化趋势更为接近，特别是在高围压阶段。为了更准确地比较两种强度准则对三轴压缩实验的预测效果，这里给出了不同围压下预测结果与实验结果（根据实验数据插值）的相对偏差值，如表3 所示。

根据现有数据（图5 和表3）的分析可以看出，在围压σ3为1 MPa 和5 MPa 时，线性M-C 准则、幂函数M-C 准则的预测结果与三轴压缩实验数据的相对偏差绝对值接近，最大相对偏差均在18%左右，其中线性M-C 准则的预测结果较为偏小，接近围压实验数据的下限，而幂函数M-C 准则的预测结果较为偏大，接近围压实验数据的上限；在围压σ3为10，20，30，40 MPa 和50 MPa 时，线性M-C 准则的预测偏差高于幂函数M-C 准则，且随着围压的增加偏差越来越大，最大相对偏差达到41.16%，而幂函数M-C 准则能较好地预测实验结果，最大相对偏差仅为7.42%。所以，总体而言，幂函数M-C 准则的理论预测结果与三轴压缩实验数据更为吻合，更适用于描述PBX 模拟材料的剪切破坏强度变化趋势。

4.3 细观失效特性

PBX 模拟材料是一种典型的非均质颗粒复合材料，在压制成型过程中会形成一些初始损伤和缺陷，造成较强的应力集中，当进行机械加载时，这些应力集中区容易出现颗粒脱粘（颗粒与粘结剂界面分离）、粘结剂开裂以及颗粒破碎等现象，并进一步发展形成沿晶断裂和穿晶断裂。这些微细观变形损伤特性与其对应的应力状态密不可分，所以本研究利用SEM 对PBX 模拟材料试样在不同压剪应力状态下的断口细观形貌进行了观察与分析，其结果如图6 所示。

从图6 可以看出，在压剪复合作用下，试样的剪切破坏面主要存在颗粒整体剪断、颗粒破碎、断面磨蚀以及细观裂纹等损伤失效特征，压应力对于PBX 模拟材料失效破坏的细观特性有着明显的影响：当加载角度θ为0°时，试样处于简单剪切状态，破坏以颗粒整体剪断为主，在局部位置有极少数的颗粒脱粘现象；当加载角度θ为15°时，试样开始受到压缩和剪切的耦合作用，此时尽管颗粒仍以剪切断裂为主，但部分颗粒已在压应力作用下出现破碎开裂，同时剪切断面上开始出现磨蚀；当加载角度θ为30°时，压剪耦合作用中压应力的作用进一步增加，导致大量颗粒出现破碎，且在压剪耦合作用下破碎颗粒区汇聚连接形成少量的次生张拉裂纹，剪切断面磨蚀程度加重；当加载角度θ为45°时，压应力的作用更加明显，压剪面上的这种次生张拉裂纹大量出现，且不同裂纹之间开始出现连接和贯通。随着压应力的逐渐增大，细观张拉裂纹在试样失效破坏上的作用逐渐增强，以致在加载角度θ为60°，75°，90°时，这种细观裂纹的连接和贯通已经导致试样出现宏观上的张拉裂纹，进而无法再以单一破坏面的形式发生失效。不难看出，在压剪作用下的剪切破坏中，颗粒脱粘和粘结剂开裂等细观损伤行为会受到抑制，颗粒剪断和破碎成为主导并造成试样发生穿晶断裂。

表3 预测结果与实验结果的比较Table 3 Comparison of predicted results and experimental results

图6 PBX 模拟材料剪切破坏面的细观形貌Fig.6 Mesoscopic morphology of shear fracture surfaces for PBX simulant

在压剪复合加载下，剪切破坏面上的细观损伤主要是由内摩擦作用造成的，随着压剪角度增大，压剪面上压应力的作用愈加明显，细观损伤行为呈现出渐进发展的特征，这说明压应力的增加会使材料的内摩擦作用增强，所以PBX 模拟材料的宏观抗剪强度会表现出随压应力增加而逐渐增大的变化趋势。同时，细观上的颗粒破碎和次生裂纹发展在一定程度上改变了压剪面上的内摩擦特性，造成PBX 模拟材料抵抗颗粒之间滑动摩擦和咬合摩擦的性能“劣化”，这在M-C 准则中体现为内摩擦系数的降低，从而使PBX 模拟材料剪切破坏强度变化规律不符合线性M-C 准则而更趋近于非线性的幂函数M-C 准则。

5 结论

（1）PBX 模拟材料在压剪实验中主要表现出剪切和张裂两种宏观破坏模式，当加载角度θ为0°，15°，30°，45°时主要表现为沿压剪面剪切的破坏模式，当加载角度θ为60°，75°，90°时表现为剪切和张裂的混合破坏模式。

（2）建立了用于描述PBX 模拟材料剪切破坏的幂函数M-C 准则，对于压剪实验，幂函数M-C 准则的拟合相关度明显优于线性M-C 准则，拟合相关指数达到0.996；对于三轴压缩实验，幂函数M-C 准则的预测效果同样优于线性M-C 准则，预测结果与实验数据基本吻合。

（3）随着压剪角度的增大，压应力作用增强，PBX模拟材料压剪面上会依次出现颗粒整体剪断、颗粒破碎与表面磨蚀、次生裂纹以及裂纹之间的连接贯通等损伤失效特征；在压剪作用下，压应力增加会导致材料内摩擦阻力的增大，同时颗粒破碎和次生裂纹发展会引起内摩擦系数的降低，两者综合作用是导致PBX 模拟材料剪切破坏强度随压应力增加而非线性增加的重要原因。