土壤表面电场对黄土母质发育土壤水分入渗特性的影响及模拟*

杨志花 胡斐南 刘婧芳 许晨阳 马任甜 王子龙 赵世伟†

（1 中国科学院水利部水土保持研究所，黄土高原土壤侵蚀与旱地农业国家重点实验室，陕西杨凌 712100）

（2 西北农林科技大学资源环境学院，陕西杨凌 712100）

（3 中国科学院大学，北京 100049）

土壤水分入渗是地表水转化为土壤水的一个重要过程，它不仅决定着地表径流量的产生进而影响土壤侵蚀状况，而且也决定着灌溉水的利用效率进而影响作物产量[1-2]。因此，研究土壤水分入渗变化规律及机制，对合理利用和调节土壤水库功能，增强土壤水分保蓄能力，减少土壤侵蚀，提高作物产量具有重要的科学价值和实践意义[3]。

土壤水分入渗主要受土壤有机质含量、容重、质地、结构稳定性、土壤温度及水质等因素的影响。其中结构稳定性对土壤水分入渗的影响至关重要。团聚体作为一种良好的土壤结构体，其破碎后会释放大量细颗粒物质，堵塞土壤孔隙，降低土壤入渗能力[4]。土壤孔隙是水分入渗过程的主要通道，孔隙的大小和分布决定着水分入渗的快慢。对于某一特定土壤，水分入渗过程中土壤孔隙状况受土壤结构稳定性的强烈影响。因此，良好的土壤结构稳定性对土壤水分保蓄具有重要意义。新近的研究发现：介观尺度土壤内力作用（静电斥力，水合斥力和范德华力）所产生的压强可高达数百个大气压，是团聚体破碎的主要推动力[5-7]，进而对土壤水分入渗过程带来影响。土壤内力作用受到土壤溶液电解质浓度和类型的影响。吴忠东和王全九[8]通过研究入渗水矿化度对土壤入渗特征的影响，发现在一定浓度范围内，随Na+溶液浓度的升高，土壤的渗透性增强。郭太龙等[9]研究发现随着入渗水的矿化度的增加，土壤的入渗能力增加。通过定量调控土壤表面电场强度，Yu 等[10]研究发现，随着本体溶液电解质浓度的降低，紫色土土壤表面电场的增强，土壤水分入渗速率减小。可见，土壤表面电场将会深刻地影响水分入渗过程。

黄土高原是全世界水土流失最为严重的地区之一，降雨较少且集中。提高该区有限水的利用效率对维系区域生态环境安全和绿色农业高效发展具有重要的意义。降雨或灌溉水进入土壤后，首先使得土壤本体溶液电解质浓度降低，土壤表面电场增强，团聚体稳定性降低，并最终影响水分入渗过程。尽 管有关黄土区水分入渗、有效性及其影响因素的研究较多[11-12]，但是关于该区土壤水分入渗过程中土壤界面性质（土壤颗粒表面电场、电位）变化及其对入渗特性的影响尚不清楚，同时考虑土壤表面电场作用后经典水分入渗模型的适用性还有待进一步验证。

因此，本研究以两种典型的黄土母质发育土壤—塿土和褐土为研究对象，通过理论计算与试验验证相结合的方法，旨在探究土壤表面电场对水分入渗的影响，并采用经典水分入渗模型进行拟合。研究结果可为黄土高原土壤水分入渗的内部调控新技术提供理论参考。

1 材料与方法

1.1 供试材料

以塿土和褐土为供试土壤，分别采自陕西杨凌和周至的农田表层土壤（0～20 cm），去杂风干后过1 mm 筛装袋备用。供试土壤的基本性质列于表1，其中土壤有机质采用重铬酸钾外加热容量法测定，pH 采用电极法（土水比：1∶2.5）测定，阳离子交换量（CEC）和比表面积（SSA）采用物质表面性质联合测定法测定[13-14]，土壤颗粒组成采用MS2000激光颗粒分析仪（马尔文公司，英国）测定。

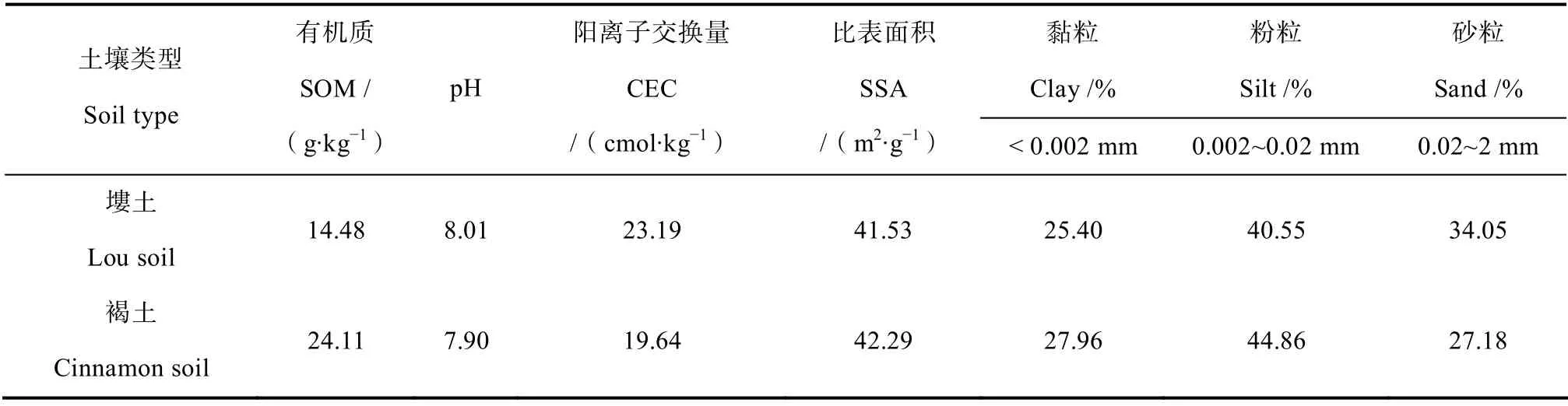
表1 供试土壤基本理化性质 Table1 Basic physical and chemical properties of the soils tested

1.2 样品制备

为定量表征土壤电场对土壤水分入渗特性的影响，首先需要对土壤样品进行表面处理，制备成单一离子饱和样品，以排除其他杂质离子的干扰[5]。由于Na+在土壤颗粒表面较弱的极化能力，本研究中使用Na+饱和样品[10,15]。Na+饱和样品的制备过程如下[6,16]：首先，称取1.5 kg 风干土壤样品，置于5 000 mL 大烧杯中，加入0.5 mol·L-1NaCl 溶液定容至5 000 mL，搅拌12 h 后离心（4 500 r·min-1，5 min），弃去上清液，重复上述操作3 次；之后，将NaCl 溶液换为去离子水，重复上述步骤，洗去溶液中多余盐分。最后将饱和样品在65°C 下烘干，研磨过1 mm 筛备用。

1.3 试验装置与方法

本试验装置为一组自制的有机玻璃柱[10]，由底座、长方体装土槽和加液槽3 部分构成。底座为长20 cm、宽15 cm、厚3 cm 的长方体有机玻璃板。长方体装土槽内腔长、宽、高分别为3 cm、1 cm 和20 cm，底端以带有2 mm 的小孔隔板隔开，以保证装置内土壤的通气性。上部加液槽高5 cm，用于加入入渗溶液。长方体装土槽和加液槽之间以带有直径2 mm 小孔的隔板隔开，隔板上方放置数颗小玻璃珠，以减少液体注入时对表面土壤的冲击。

本研究采用一维定水头垂直积水入渗法测定入渗特性。参照实际土壤容重和入渗装置的体积，将试验土壤容重设置为1.25 g·cm-3，装样时每2 cm 分层填装[10,17-18]，层间打毛。土柱底部铺垫铁丝网和滤纸，防止土粒漏失。填装好后，用带有刻度的有机玻璃盖板盖好，侧方涂抹凡士林密封。入渗过程中采用先密后疏原则依次记录湿润锋运移位置变化及对应入渗时间。入渗试验结束后，快速取下盖板，每隔0.5 cm 取出各段土体，分别称量烘干前后的土体质量，计算土壤含水率、土壤累积入渗量及水分入渗速率[17,19-21]。

本研究中，土壤表面电场通过本体溶液电解质浓度来定量调控。根据经典双电层理论，采用一系列不同浓度的NaCl 溶液作为入渗溶液来调节土壤电场。为了对比分析土壤电场作用对水分入渗的影响，使土壤电场在一个较宽的范围内变化，试验中将NaCl 溶液浓度梯度设置为1、0.1、0.01、0.001和0.0001 mol·L-1。

1.4 数据计算与分析

根据双电层理论，在1∶1 型电解质溶液中，土壤表面电位可由下式来计算[22]：

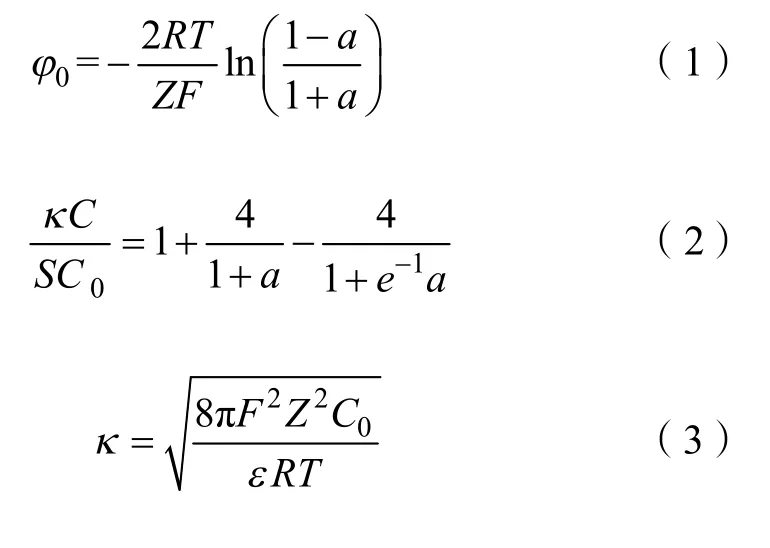
式中，φ0表示土壤表面电位，V；Z表示电解质阳离子的化合价；R表示气体常数，8.31 J·mol-1·K-1；T表示绝对温度，298 K；F表示法拉第常数，96 485.34 c·mol-1；a表示方程中间变量；κ表示德拜-休克尔系数，1·dm-1；C表示阳离子交换量，cmol·kg-1；C0表示本体溶液中阳离子的平衡浓度，mol·L-1；S表示比表面积，m2·g-1；ε表示介电常数，8.9×10-10C2·J-1·dm-1。

距离土壤颗粒表面x处的电位和场强计算公式如下：

式中，φ（x）表示距离颗粒表面x处的电位，V；x表示双电层中距离颗粒表面的距离，nm；b表示中间变量；E（x）表示距离表面x处的电场强度，V·m-1。

对于匀质土壤适用的入渗模型有Kostiakov 模型[23]和Philip 模型[24]，其公式分别如式（7）、式（8）所示：

式中，t为入渗时间，min；I为累积入渗量，cm（本研究以g 来表示）；A，K皆为拟合得到的经验常数，A反映土壤入渗能力的衰减速度[25]，K为入渗开始后某种意义上的第一个单位时段末的累积入渗量，在数值上等于第一单位时段末的入渗速度；S为吸渗率，cm·min-0.5，指土壤依靠毛管力吸收和释放液体的能力，反映土壤前期入渗能力[26-27]。

本研究采用Excel 2003 进行数据处理，Origin 9.1 进行软件作图和土壤入渗模型拟合，SPSS 21.0软件进行统计分析。

2 结果与讨论

2.1 表面电化学性质

根据双电层理论，本体溶液电解质浓度的变化将影响土壤表面电位和颗粒周围的电场。根据测定的比表面积和阳离子交换量，不同电解质浓度下土壤表面电位可通过式（1）～式（3）定量计算，结果如表2所示。由表2可知，在两种土壤中，随着本体溶液电解质浓度的降低，土壤表面电位绝对值增大。例如，在高电解质浓度 1 mol·L-1时，塿土和褐土的表面电位分别为-121.00 mV 和-112.25 mV；当电解质浓度降低至0.0001 mol·L-1时，塿土和褐土的表面电位高达-349.99 mV 和-340.56 mV。电解质浓度从1 mol·L-1降低至0.0001 mol·L-1，两种土壤的表面电位绝对值增长了1.89 倍、2.03 倍。

依次将一系列的表面电位数值代入式（4）～式（6）中，得到不同电解质浓度下的土壤颗粒周围电场分布曲线，如图1所示。从图中可以看出，随着距离的增大，电场强度不同程度的减小。各电解质浓度下，土壤颗粒表面处的电场强度皆高达108V·m-1。在两种土壤中，随着电解质溶液浓度的增加，土壤颗粒周围相同距离处的电场强度减小，表面电场的作用距离急剧缩短。例如，当电解质浓度为0.001 mol·L-1时，电场作用距离达140 nm 以上；但当电解质浓度为1 mol·L-1时，电场作用距离压缩至15 nm 以下。这表明，通过改变本体溶液电解质浓度即可调控土壤颗粒周围电场强度与分布。

表2 不同电解质浓度下的土壤表面电位 Table2 Soil surface potential relative to electrolyte concentration

图1 不同电解质浓度下土粒周围电场强度分布 Fig.1 Distribution of soil electric field strength around soil particles relative to concentration of electrolyte

2.2 土壤电场对黄土水分入渗特性的影响

2.2.1 湿润锋运移位置的变化 湿润锋是指水分下渗过程中湿润层下缘明显的干湿交界锋面，其运移速度的大小可反应土壤的输水能力[28]。湿润锋位置的变化可直观地反映土壤水的垂向运动特征。图2给出了不同电解质浓度条件下湿润锋运移位置的变化情况。从图中可以看出，电解质浓度对湿润锋的运移速度具有重要影响。随着电解质浓度增大，湿润锋运移速度加快。例如，当测定时间为300 min，电解质浓度为0.000 1 mol·L-1时，塿土和褐土的湿润锋运移位置分别为2.05 cm 和2.15 cm；但当对应的浓度为0.1 mol·L-1时，运移位置分别为8.51 cm和6.08 cm。此外，当电解质浓度低于0.01 mol·L-1后，不同浓度条件下湿润锋运移速度较为缓慢且接近。例如，以塿土为例，当测定时间为300 min 时，土壤本体溶液电解质浓度为0.01 mol·L-1时，塿土中湿润锋的运移位置为2.84 cm；而当对应的电解质浓度分别为0.001 mol·L-1、0.000 1 mol·L-1时，湿润锋的运移位置分别为2.08 cm、2.05 cm。同时，当溶液浓度小于0.01 mol·L-1后，湿润锋运移位置几乎不再随入渗历时的变化而发生改变。这表明0.01 mol·L-1是土壤水分入渗过程的临界浓度。该条件下湿润锋运移速度非常缓慢，说明此时的土壤水分运动受到土壤电场的极大限制。

图2 不同电解质浓度下湿润锋位置的动态变化 Fig.2 Dynamics of wetting front position relative to concentration of electrolyte

2.2.2 累积入渗量的变化 土壤水分累积入渗量是指单位面积流入土壤的水分量，是土壤水分运动的主要特征之一。图3给出了各电解质浓度下累积入渗量随着测定时间的变化情况。从图中可以看出，电解质浓度对水分累积入渗量具有重要影响。当浓度较高时，累积入渗量随着入渗时间的延长而增加，曲线斜率由陡逐渐变缓；而当浓度较低时（＜ 0.01 mol·L-1），累积入渗量变化曲线较为接近。例如，当测定时间为300 min，电解质浓度为0.001 mol·L-1时，塿土和褐土的累积入渗量分别为2.04 g 和1.62 g；但当电解质浓度升高至0.01 mol·L-1和0.1 mol·L-1时，塿土两浓度下的累积入渗量分别为3.59 g 和10.69 g，与0.001 mol·L-1时的累积入渗量相比，增加幅度分别为75.98%和424.02%；褐土两浓度下的累积入渗量分别为2.22 g、7.54 g，增加幅度分别为37.04%、365.43%。这表明土壤电场对累积入渗量的影响十分明显。电解质浓度0.01 mol·L-1是影响累积入渗量的临界点。对比图2，累积入渗量和湿润锋随时间变化的趋势基本一致。

2.2.3 入渗速率的变化 入渗速率是指单位时间通过地表单位面积入渗至土壤中的水量[29]。图4为塿土和褐土在不同电解质浓度下入渗速率随时间的变化情况。由图4可知，不同电解质浓度条件下的入渗速率随时间的变化趋势相同：在入渗初始阶段（30 min 内），各浓度下入渗速率皆急剧减小；在入渗稳定前阶段（30～250 min），随电解质浓度的降低，电场的增强，入渗速率皆缓慢减小；在入渗稳定阶段（250～400 min），入渗速率逐渐趋于稳定，该稳定值即土壤的稳定入渗速率。在塿土中，30 min 时，1 mol·L-1和0.000 1 mol·L-1下的入渗速率分别为0.060 cm·min-1和0.014 cm·min-1，稳定入渗速率分别为0.010 cm·min-1和0.002 cm·min-1。而在褐土中，30 min 的入渗速率分别为0.057 cm·min-1和0.009 cm·min-1，最后稳定在0.017 cm·min-1和0.003 cm·min-1。这表明水分入渗速率强烈地受到土壤表面电场的影响。

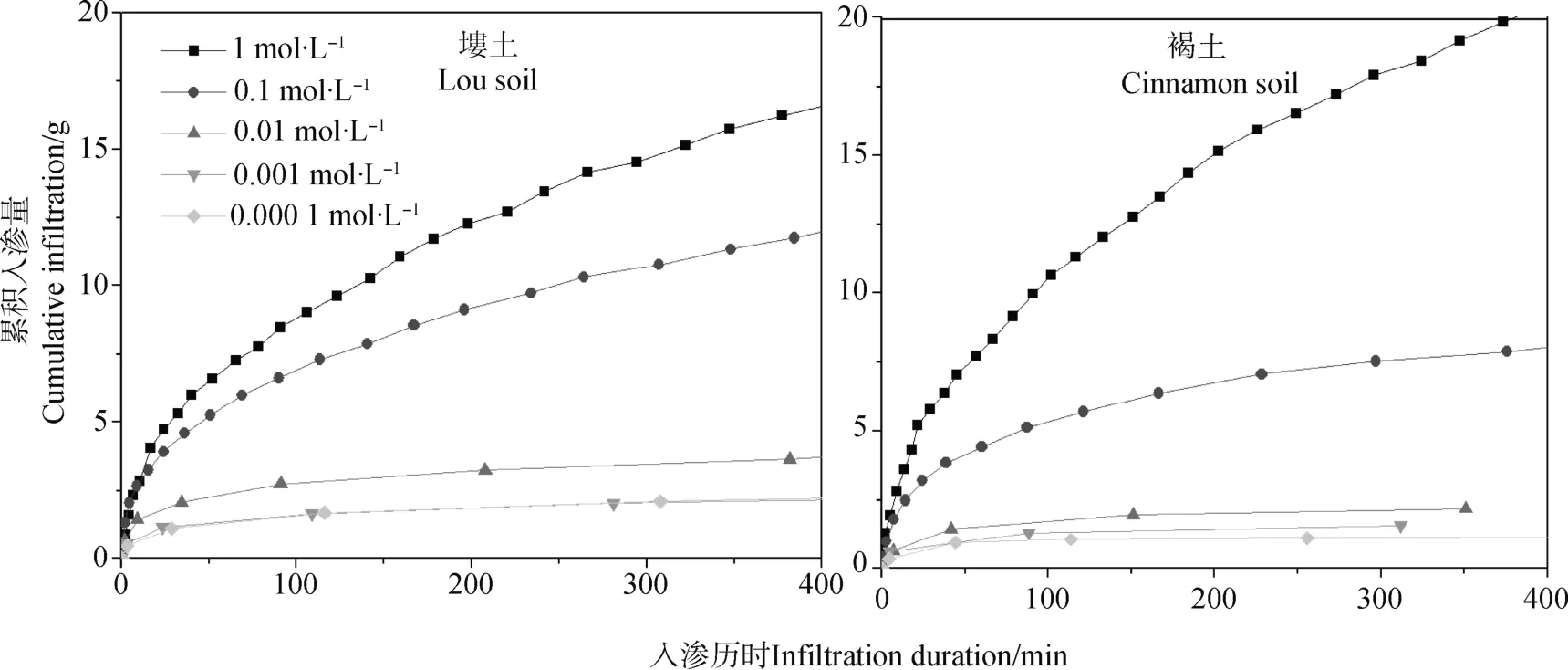
图3 不同电解质浓度下累积入渗量的动态变化 Fig.3 Dynamics of cumulative infiltration relative to concentration of electrolyte

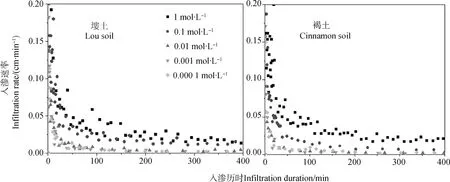
图4 不同电解质浓度下入渗速率的动态变化 Fig.4 Dynamics of infiltration rate relative to concentration of electrolyte

2.3 黄土水分入渗过程的模拟

为定量分析不同电解质浓度对黄土入渗性能的影响，采用Kostiakov 模型和Philip 模型试验数据进行拟合。对两种土壤的累积入渗量结果分别进行两种模型的拟合，拟合结果如表3所示，为便于表述，表中Kostiakov模型和Philip 模型分别简称为K 模型和P 模型。

由表3可以看出，两种土壤各电解质浓度下，两模型的决定系数R2均较大，Kostiakov 模型决定系数最大值为0.999，最小值为0.778；P 模型最大值为0.997，最小值为0.785，即Kostiakov 模型和Philip 模型均可对两种土壤累积入渗量随测定时间的变化情况做出较好的拟合，但比较决定系数R2可知，Kostiakov 模型拟合结果更好。随着电解质浓度的降低，Kostiakov 模型参数A略有减小，即入渗速率的衰减速度减缓，说明随着土壤表面电场的增强，入渗速率变化减小；参数K减小，第一单位时段末的累积入渗量或者第一单位时段末的入渗速率在持续减小；Philip 模型中，随着电解质浓度的降低，参数S减小，即吸湿率持续减小，前期入渗力减弱。

为进一步分析两种模型的适用性，对两种模型的预测值与实测值进行线性回归分析。本研究中，通过分析拟合统计特征值（R2、残差平方和均方根误差RMSE 值），比较模型的拟合精度[30]，分析模型适用性。分析结果如表4所示。表中R2越大，残差平方和越小，RMSE 值越小，说明模型的拟合效果越好。如表4所示，综合上述多个统计值发现，在两种土壤中，各个浓度下的累积入渗量随测定时间的变化，Kostiakov 模型的拟合结果更优。

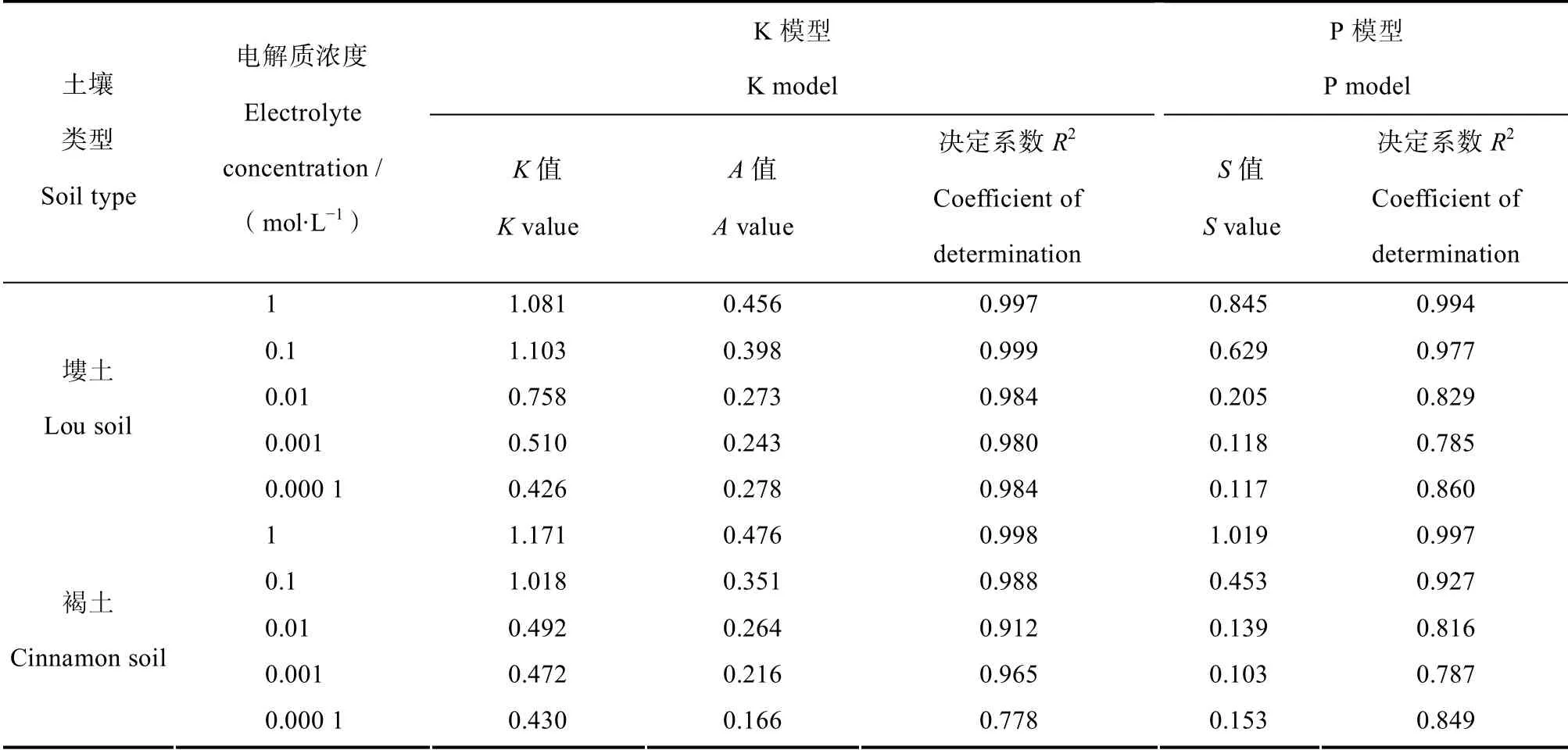
表3 累积入渗量随测定时间变化情况两种模型拟合结果 Table3 Comparison of two models fitting temporal variation of cumulative infiltration

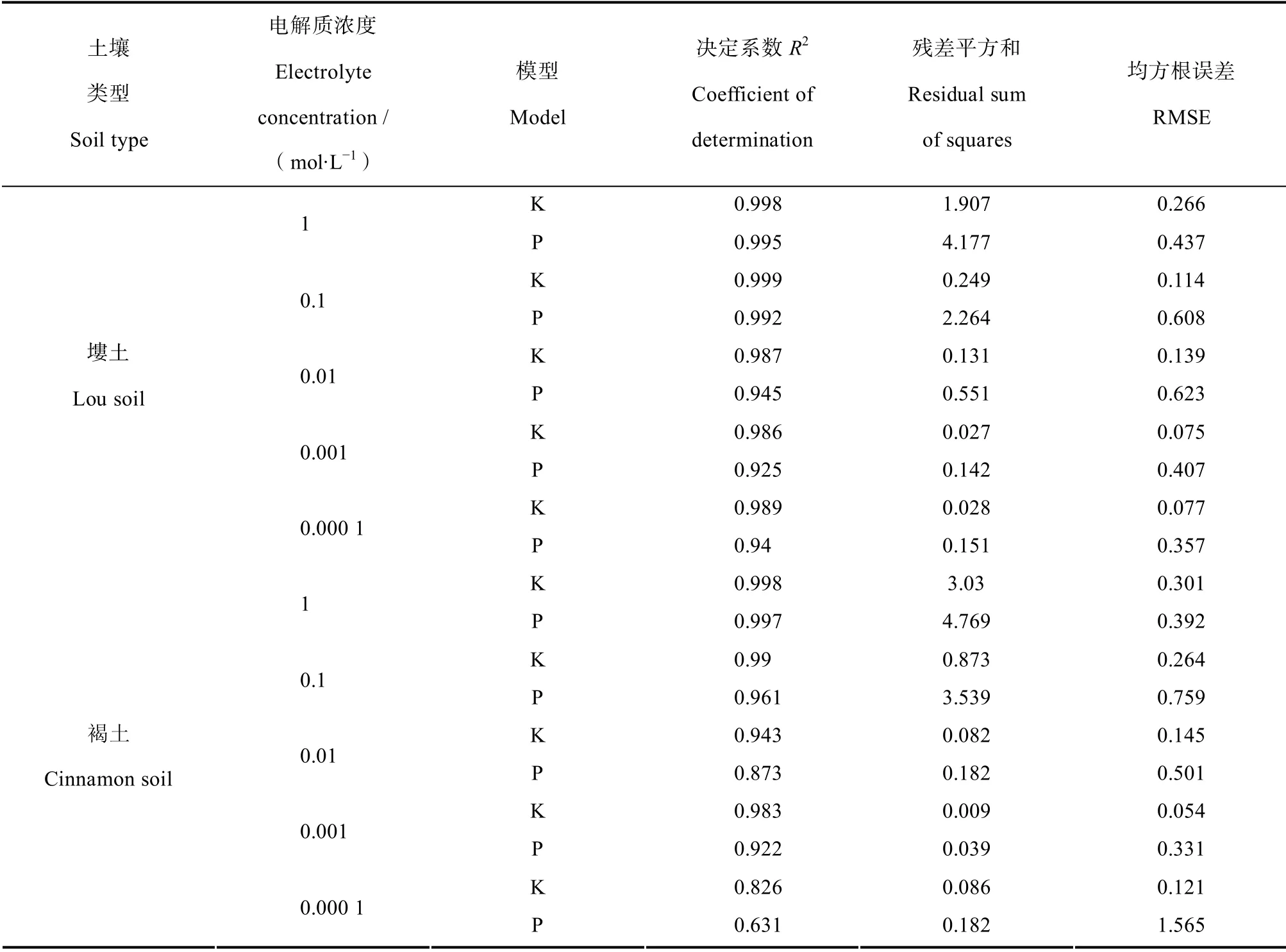
表4 两种模型下累积入渗量实测值与预测值回归分析统计值 Table4 Regression statistics of measured and predicted cumulative infiltrations relative to model

2.4 土壤电场对水分入渗特性的影响

土壤表面电场对土壤水分入渗特性具有重要影响[10]。本研究发现，随着本体溶液电解质浓度降低，土壤表面电位升高，颗粒周围电场增强（图1）。不同电解质浓度条件下，土壤水分入渗特性不尽相同，表现为：随本体溶液电解质浓度的减小，湿润锋运移速度、水分入渗速率和累积入渗量均减小（图2～图4）。这表明，随着本体溶液电解质浓度的降低，土壤电场的增强，土壤水分运动受到极大地限制，这与Yu 等[10]的研究结果一致。也有研究表明微咸水中的盐分可以促进土壤水分的入渗[31]。入渗时间相同的情况下，微咸水入渗的累积入渗量以及湿润锋运移深度均大于淡水入渗[32]。以上结果主要定性地归因于本体溶液电解质浓度对土壤颗粒双电层结构的影响，进而影响水分入渗[10]。随着本体溶液电解质浓度的增加，土壤颗粒扩散双电层受到反号离子较大程度地压缩，进而降低土壤颗粒周围电场强度和分布[33]。本研究中，根据经典双电层理论，定量计算了不同电解质浓度条件下颗粒表面电位和土壤颗粒周围电场强度的大小及分布。随着本体溶液电解质浓度的降低，土壤电场增强，颗粒间的强电场作用将会深刻地影响团聚体的稳定性，继而影响土壤孔隙状况，并最终影响土壤水分运动[10]。电解质浓度变化所引起的较小的颗粒表面电场的变化使得宏观上的入渗特性产生了较大的变化。

随入渗时间延长，入渗速率减小，湿润锋运移速度减慢，累积入渗量增加幅度变缓（图2～图4）。这主要是因为当入渗液体进入土体后，上层湿土的毛管吸力作用强于下层，对主要依靠重力的下渗过程产生抑制作用，加上表层团聚体破碎后造成的结皮阻碍了土层气体排出，使得入渗能力随入渗过程的进行有一定程度的减弱[34]。此外，从图2～图4也可以看出，随着电解质浓度的降低，相同时间间隔下各入渗特性参数变化量均减小。这主要是因为低浓度条件下土壤电场较强，入渗溶液对土壤团聚体结构破坏力较大[6]，土壤孔隙变小，入渗能力的衰减速度相比高浓度、大孔隙下的衰减速度较慢[26]，故Kostiakov 模型参数A随电解质浓度降低略有减小，即随电解质浓度降低，土壤表面电场的增强，入渗速率的衰减速度减缓。随着电解质浓度的降低，Philip 模型参数S减小，即吸渗率持续减小，Kostiakov 模型参数K减小，即前期入渗能力减弱，可解释为表层土壤随着被入渗溶液浸湿，土壤电场急剧增大，团聚体结构破碎而释放大量小颗粒，阻塞土壤孔隙，致使土壤水力传导度降低[6]。

3 结 论

土壤表面电场强烈地影响上述两种黄土母质发育土壤的水分入渗特性。随着电解质浓度的降低，土壤颗粒的表面电位（绝对值）和电场的急剧增大，导致土壤湿润锋运移速度、入渗速率和累积入渗量减小。电解质浓度0.01 mol·L-1是影响土壤入渗过程中各特征参数的临界点。当电解质浓度 ＜ 0.01 mol·L-1，塿土和褐土的表面电位绝对值大于 233 mV 和223 mV 时，土壤水分入渗特性参数随时间的变化曲线较为接近。通过对累积入渗量随测定时间的变化情况进行拟合分析，发现Kostiakov 模型和Philip模型均可对这一变化情况做出较好的拟合。综合各统计值比较分析后发现，在两种土壤中Kostiakov模型拟合效果更优。