多系统组合精密单点定位性能分析
2020-01-14王璐桂占飞
王璐,桂占飞
(西安市勘察测绘院,陕西 西安 710000)
1 引 言
近年来,全球导航卫星系统发展迅速,美国的GPS导航系统目前最为成熟,已有24颗在轨卫星实现全球覆盖。中国自主研发的北斗卫星导航系统截至2018年底,完成19颗卫星发射组网,北斗三号系统基本已经建成,向全球提供服务;计划2020年前后,完成30颗卫星发射组网,全面建成北斗三号系统。欧盟研制和建立的伽利略卫星导航系统在轨卫星达到18颗,于2016年12月15日投入使用,计划到2020年,伽利略卫星导航系统在轨卫星将达到30颗[1]。精密单点定位方法不受地面基准站以及作业距离的约束,可直接获取国际地球参考框架下的高精度地面绝对坐标,在地壳形变监测、低轨卫星定位、气象研究等领域得到广泛应用[2]。但当观测受地形限制,卫星信号遮挡严重时,可见卫星数量较少,单系统单点定位性能很差,并且单系统的浮点解收敛速度较慢,影像解算精度。多系统组合可以增加可见卫星数,增强空间几何强度,加快模糊度固定时间,在连续性、可靠性和定位精度方面较单系统都大大提高[3]。随着各国导航系统的逐步完善,多系统组合导航定位已成为必然趋势。目前,国内外许多学者对多系统组合定位方法都进行了研究[4,5],研究表明,GPS/BDS、GPS/GLONASS、GPS/GALILEO组合系统覆盖性能较GPS、GLONASS、GALILEO、BDS单系统优势明显,但对于三种系统融合单点定位方法研究还尚未完善,本文在GPS精密单点定位方法的基础之上,对BDS,GPS,GALILEO多系统组合单点定位算法和定位精度等方面进行了分析研究,并与单系统和双系统定位精度进行了对比。
2 BDS/GPS/GALILEO时间与空间基准的统一
由于各系统有独自稳定的时间与坐标系统,要实现各系统之间的组合,首先要解决时间与空间基准的统一问题[6]。由于世界协调时(UTC)与各导航系统的时间系统存在一定的联系,因此可以基于UTC作为桥梁,实现各系统时间基准的统一。GPS时(GPST)以原子秒长作为时间尺度基准,起算时刻与1980年1月6日协调时零时刻一致,同UTC存在整秒偏差和几个ns的基准钟系统偏差,GPST与UTC之间关系如下:
GPST=UTC+ns-19s
(1)
式中,ns为UTC相对于国际原子时(TAI)的跳秒。伽利略系统时(GST)起始历元为1999年8月22日UT零时,与UTC之间存在 13 s的偏差,GST与UTC之间关系如下:
GST=UTC-19s+ns
(2)
ns为跳秒值。北斗卫星导航系统采用的时间基准为北斗时(BDS),起算时刻与2006年1月1日UTC零时一致,GPST和BDT与国际UTC相差整数跳秒值,但由于起始历元不同,存在 14 s的偏差:
BDT=GPST-14s
(3)
GPS、GALILEO、BDS分别采用WGS-84、GTRF、CGCS2000作为参考坐标系,WGS-84、GTRF、CGCS2000都与不同历元下ITRF框架联系,因此通过对不同ITRF框架的转换实现各系统之间空间基准的统一。
3 BDS/GPS/GALILEO组合单点定位的数学模型
在单系统单点定位中,通常采用无电离层线性组合观测值消除一阶电离层延迟,对于一颗卫星s和一个测站r,其观测方程表示为[7]:
(4)
(5)

(6)
(7)
(8)
(9)
(10)
(11)
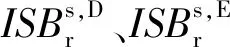
4 数据处理策略
BDS,GPS,GALILEO多系统组合精密单点定位,观测方程中待估参数包括:测站三维坐标、接收机钟差、对流层延迟误差、系统间偏差等。数据处理中,参数估计采用扩展卡尔曼(Kalman)滤波[8],其中,接收机静态坐标、系统偏差和模糊度都作为常量估计,接收机动态坐标和接收机钟差当作白噪声处理,对流层延迟通过随机游走过程模拟,通过在全球多系统定位服务实验网(MGEX)获取多系统精密星历和精密钟差文件消除轨道和卫星钟差等影响[9]。具体的处理策略如表1所示:

数据处理策略 表1
5 实验与结果分析
本文实验选取40个MGEX跟踪站2017年7月19日~2017年7月21日三天的观测数据对BDS/GPS/GALILEO组合单点定位分别进行静态和动态实验分析,40个测站分布如图1所示。观测数据采样间隔为 30 s,截止高度角设为10°,通过以单系统BDS、双系统GPS+BDS和多系统GPS+BDS+GALILEO为例,通过计算分析,对这几种方案在静态和动态定位模式下的卫星可见数量、收敛速度和定位精度进行比较。

图1 40个测站分布图
在实验观测时长内,以BDS卫星数较多的JFNG测站为例,JFNG站可见卫星数量在BDS、GPS+BDS、GPS+BDS+GALILEO三种系统方案下变化情况如图2所示。其中,单系统BDS中,可见卫星数平均值为7.86,;双系统GPS+BDS中,可见卫星平均值为16.83;三系统GPS+BDS+GALILEO中可见卫星数平均值为23.77。显而易见,GPS+BDS+GALILEO系统组合模式下可见卫星数明显优于双系统和单系统的可见卫星数。图3给出了JFNG测站位置精度衰减因子(PDOP)值变化情况。由图中结果可知,GPS+BDS+GALILEO系统组合下的PDOP值较单系统BDS和双系统GPS+BDS明显降低,说明GPS+BDS+GALILEO组合系统的卫星结构强度强于单系统和双系统的卫星结构。

图2 可见卫星数
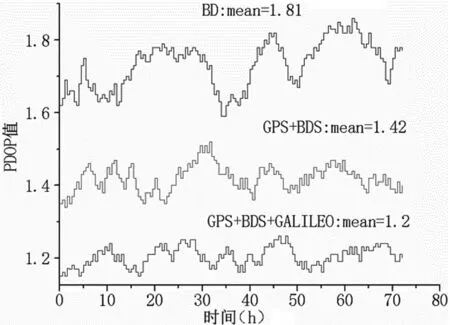
图3 PDOP值
以JFNG、GMSD两个测站为例,图4给出了两个测站在BDS、GPS+BDS、GPS+BDS+GALILEO三种模式下静态定位结果,由图可见,BDS的收敛速度最慢,需要约 45 min左右收敛到 0.05 m,GPS+BDS+GALILEO组合系统下,可见卫星数量多,空间几何强度高,收敛速度快,收敛时间明显减少,20 min左右在东、北、垂直方向均能收敛到 0.05 m。

图4 JFNG和GMSD测站多系统模式下静态定位性能
将测站JFNG的观测数据,每半小时作为一个时段,以IGS获取的坐标作为真值,分别计算每个时段定位误差在东、北、垂直三个方向的均方根(RMS)。图5为测站JFNG分别在BDS、GPS+BDS、GPS+BDS+GALILEO系统下4小时内定位精度RMS值的变化柱状图。由图可见,半小时内,在三系统GPS+BDS+GALILEO下,东、北、垂直三个方向的RMS分别为 0.09 m,0.1 m,0.07 m,很快达到 0.1 m之内,较单系统和双系统都有显著提升。4小时后,BDS系统下,测站在东、北、垂直方向的RMS分别为 0.10 m,0.06 m,0.13 m;GPS+BDS系统下,测站在东、北、垂直方向的RMS分别为 0.07 m,0.06 m,0.05 m;在GPS+BDS+GALILEO系统下,测站在东、北、垂直方向的RMS分别为 0.04 m,0.03 m,0.03 m。可见在单系统、双系统、三系统组合定位下,北方向的定位精度较高,RMS值均可达到 0.07 m以内,但在东方向和垂直方向,单系统BDS定位RMS值明显偏大,超过 0.1 m。通过三种模式的比较可以看出,在GPS+BDS+GALILEO组合定位下,4小时后,东、北、垂直三个方向的定位精度明显提高,RMS均在 0.05 m以内,较单系统BDS分别提升了64%,32%,71%,其中垂直方向的改善最为明显。

图5 多系统静态单点定位在不同方向的RMS值
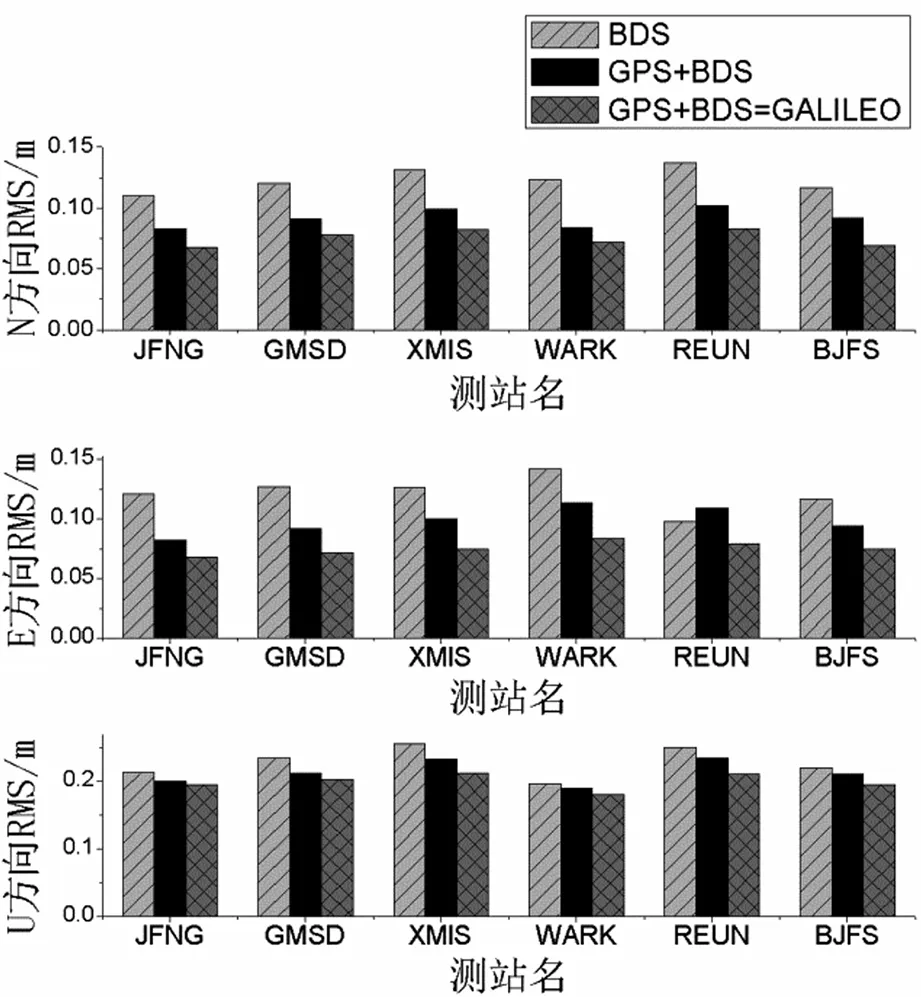
图6 多系统动态单点定位在不同方向的RMS值
为了分析多系统组合方案下,动态单点定位的性能,对JFNG、GMSD、XMIS、WARK、REUN、BJFS六个测站2017年7月19日24小时的观测数据采用BDS、GPS+BDS、GPS+BDS+GALILEO系统三种模式分别进行动态定位,通过上节的数据处理策略进行计算,分别得到测站在这三种系统模式下东、北、垂直三个方向的RMS值。图6分别给出了6个测站在不同系统下东、北、垂直三个方向收敛后的RMS值结果。通过图的对比分析可见,三种模式下,测站在东、北方向的RMS均可达到 0.15 m以内,在垂直方向RMS达到 0.3 m以内,同单系统和双系统模式相比,GPS+BDS+GALILEO组合系统在东、北方向的RMS基本在 0.1 m以内,达到厘米级,有明显的优势。GPS+BDS+GALILEO组合模式同BDS单系统模式相比,在东、北、垂直三个方向的RMS值分别平均提高了35%、41%、14%。
为了评估多系统组合精密单点定位在全球范围内的性能,表2给出了40个站的平均结果(截止高度角为10°)。由表可知,三系统组合单点定位在静态模式下定位精度优于 2.4 cm,在动态模式下定位精度优于 6.1 cm,和单系统BDS、双系统GPS+BDS单点定位相比,定位精度明显提高。

40个站平均定位精度与收敛时间 表2
6 结 论
本文对BDS/GPS/GALILEO多系统组合的数学模型进行分析,提出了针对三种系统多种观测数据的处理策略,通过实验分析得出:相比较单系统BDS、双系统GPS+BDS,GPS+BDS+GALILEO三系统组合模式在同一观测段的可见卫星数量增多,卫星几何结构得到改善,定位收敛速度提升明显,无论是在静态定位模式下,还是在动态模式下,GPS+BDS+GALILEO三系统组合精密单点定位精度和收敛时间均有明显改善,改善率为25%~49%。
