基于遗传算法柔性机械臂系统建模和控制优化设计

2020-01-14张哲鞠剑平唐剑隐

中国设备工程 2019年24期

张哲，鞠剑平，唐剑隐

（湖北商贸学院机电与信息工程学院智能制造教研室，湖北武汉 430079）

柔性机械臂系统是基于传统刚性机械臂应用而产生的一种机械控制系统，其虽然具有设备质量轻、作业耗能低和荷载/自重比较高的特点，然低频率、大幅度的弹性振动使得其定位精度和操作效率受到较大影响。

1 遗传算法的基本内涵

遗传算法以适应度值进行优化计算的对象，在选择、交叉和变异操作下，实现了最优个体和最优解的有效搜寻。与传统算法方式相比，遗传算法无须函数导数等信息的辅助支撑，在解空间最大个体的搜索和适应度控制的同时，实现了一代又一代的进化，具有较高的全局优化能力和隐含并行能力。

2 基于遗传算法的柔性机械臂系统建模

2.1 系统总体模型设计思路

柔性机械臂的动力系统极为复杂，故而其在总体模型建立中具有一定的非线性和强耦合性（见图1）。本文柔性机械臂的动力系统控制优化设计以遗传算法为基础，进行Euler-Bernouli 梁模型、柔性机械臂近似模型、动力系统模型的构建，并在ISE 准则或ISTE 准则的应用下，进行控制优化和性能指标选取，确保其系统结构控制指标的最优化。

图1 柔性机械臂应用

2.2 Euler-Bernouli 梁模型

以单连杆柔性机械臂为研究对象（如图2），在应用过程中，直流电机和减速器是其驱动的主要支撑。在其运动平面内，机械臂会围绕中心点O 进行水平运动；此时与横截面相比，梁长具有较大的尺度规格，故可将其作为Euler-Bernouli 梁，并对其进行模型处理。

Euler-Bernouli 梁模型构建可先对电机与梁体的连接方式进行改变，使其保持在刚性连接状态，并确保其截面为均匀矩形；然后再在梁体形状优化的基础上，实现负载实际的有效计算。该模型体系下，梁体的长度和高度分别用L和H 表示，并将矩形几截面宽设置为B，梁体端部质量负载为Mp；此时，在考虑梁体刚性转角θ 和弹性变形μ的基础上，可将柔性机械臂的水平转动y 视为大范围刚性转动和小范围梁的弹性变形的叠加。即：

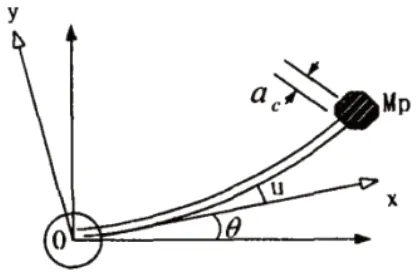
图2 单连杆柔性机械臂模型

此时，Euler-Bemouli 梁的振动方程为：

式中，E 和I 分别代表了了Euler-Bemouli 梁的体弹模量和转动惯性；而梁体抗弯刚度以EI 表示。另外，ρ 和S分别表示梁体单位长度的质量密度和梁截面面积。

2.3 柔性机械臂近似模型

柔性机械臂有限段差分近似模型构建中，依据有限差分方法，则柔性机械臂的振动方程可进一步微分，实现柔性机械臂梁沿长度方向的均匀分段。若将微分后的每段柔性机械臂△x以L/n 进行代替，且在重新定义xi、yi、Si和βi的基础上，可实现柔性机械臂振动方程和边界条件的微分简化（图3）。

图3 机械臂的柔性臂杆结构模型图

2.4 动力系统模型

直流电机、减速器是其动力系统的重要组成。若柔性机械臂系统处于工作状态，则电机转子转动惯量Jm、减速器侧的转动惯量JL、阻尼系数Bm、电机桩距系数Kt、电动势常数Ke、电枢电阻R 和减速比r 等都会对直流电机及减速器的运作形成影响。此时，直流电机及减速器的动态方程可表示为：

2.5 系统状态方程模型

末端位置输出是柔性机械臂系统输出的基本方式。若通过 nyZ = 进行其输出矩阵表达，同时，定义q0=[θy1，y2…yn]′，状态变量，则通过差商进行微分的代替，在边界条件下，联立

式（1）（2）可知：

由此实现了系统状态方程模型的有效结算，避免了矩阵求逆的应用。式中，Jm 和Jl 分别表示电机转子组涵洞惯量和减速器侧的转动惯量。Bm 表示阻尼系数，R 和r 分别为电枢电阻和减速比，kt 表示了电机转矩系数，而Ke 为电动势常数。

3 基于遗传算法的柔性机械臂系统控制优化

3.1 控制策略选择

抑制振动是柔性机械臂控制的主要目的。本控制系统优化设计过程中，工作人员以直流电机加减速器为驱动基础，进行了其机械臂线性方程的构建，确保了柔性机械臂算法控制和状态优化的灵活处理。

3.2 实现设计变量控制

设计变量控制和指标选取是柔性机械臂控制优化的两个关键环节。最优个体适应度函数值寻找中，可将种群代数作为控制因子，然后在差商微分的基础上，进行代数优化，则其对应反馈矩阵的精度也会有所增益（见图4）。由图可知，随着种群的不断变化，最优个体适应度函数值不断变小，经过10 代左右计算，得到最优个体。

图4 遗传算法优化曲线

3.3 注重约束条件处理

本次遗传算法应用过程中，柔性机械臂系统的控制优化包含以下方面：其一，进行机械臂结构的刚度优化，在预先校核、上下限约束的条件下，实现其刚度保证。其二，实现机械臂系统稳定性的约束，确保其整体应用的安全性。其三，进行优化后梁体结构的优化，使得去具有合理的长度和宽度，具有较高的工也适用性。

3.4 进行优化结果分析

本次仿真验证中，设计人员进行了机械臂系统数值的仿真，然后在直流电机驱动下，进行单连杆系统的柔性机械臂转动，并将遗传算法所确定的手臂长度、梁截面高度、梁体宽度、弹性模量等数据应用于新设备应用。若对柔性机械臂末端变形过程进行优化，则其端部转角的阶跃响应得以有效控制。具体而言，优化后，弹性振动的时间更快，即端部转角跟踪响应的时间也有所加快（见图5）。