大尺寸混凝土构件硬化期水化热温度场

薛素铎，康广博，李雄彦，耿 岩，李金光，宋延杰

(1.北京工业大学建筑工程学院，北京 100124； 2.中国寰球工程公司，北京 100012)

由于现代建筑的体积越来越庞大，结构形式也越来越复杂，因此在很多大型工程中都可以见到大尺寸混凝土构件，其结构断面最小尺寸不小于1 m，或预计会因混凝土中胶凝材料水化引起的温度变化和收缩而导致有害裂缝产生[1]，例如混凝土箱梁、超高层建筑承重柱以及液化天然气混凝土外罐墙体等. 混凝土是一种多相多孔的非均质材料, 随着尺寸的增大其非均质性增强, 破坏的随机性增大[2],且混凝土浇筑后硬化期间，内部水泥材料水化产生大量热量，使得混凝土内部温度迅速升高，内外温差较大，导致产生温度变形，而其变形受到内外约束，从而产生较高的热应力，使结构产生开裂的风险.

Abdallah等[3]研究碾压式混凝土重力坝的热- 结构模型和温度控制方法，采用热- 结构耦合分析方法模拟位于约旦一座60 m高的碾压式混凝土重力坝的施工过程，并且比较坝体内部的实测温度分布结果和有限元模拟结果，两者吻合较好. 刘海峰等[4]依托某特大桥直径38 m、厚8 m的圆形承台大体积混凝土的施工,利用有限元软件模拟水化热生成过程,对温度、应力提出控制措施,指导实际施工. Zhou等[5]对地铁国贸站15.0 m×13.2 m×1.2 m承台浇筑期间的水化热温度场进行测量，并对试验结果与有限元计算结果进行对比分析，验证有限元温度场模拟准确性,另外分析环境温度和混凝土板的厚度变化对混凝土温度场的影响. 然而国内外研究主要集中在大坝、承台类等大型混凝土结构的水化热温度场，而这些结构常常在配合比中掺入大量的粉煤灰降低水化热，并采取内部预埋管道通水冷却等相应降温措施降低热裂风险[6]. 而涉及建筑工程中的大尺寸混凝土构件，考虑到构件强度要求，配合比中未掺加粉煤灰且未预埋管道通水降温，其温度场较大坝、承台类等大型混凝土结构在峰值温度和降温阶段降温速率方面呈现较大差异，对于大尺寸混凝土构件的水化热温度场的控制还需要进一步研究.

本文基于水泥水化反应特征，提出S型水化热模型，同时对有限元软件ABAQUS进行二次开发. 为了更加精确地模拟构件温度场，对早龄期混凝土随龄期变化的绝热温升、比热容和导热系数进行试验，将试验测得具有时变性的混凝土比热容和导热系数写入子程序中，建立试件三维实体有限元模型，对构件的温度场进行模拟. 为验证数值模拟的准确性，对2个1.5 m×1.2 m×4.0 m的大尺寸混凝土构件进行硬化期水化热温度场测试，并与数值模拟结果进行对比分析. 同时，为进一步研究拆模时间对大尺寸混凝土构件降温阶段的降温速率的影响，采用本文模型选取了拆模时间在混凝土浇筑后72、96、120、144 h进行了有限元参数分析.

1 水化热温度场理论

混凝土水化过程中，内部水泥材料发生化学反应产生大量热量，混凝土结构中的混凝土假设是均匀、各向同性的，则混凝土内部各点随时间变化的温度可以通过三维瞬态热传导方程计算[7]

(1)

式中：ρ是混凝土的密度，kg/m3；c是混凝土的比热容，J/(kg·℃)；T为温度，℃；t是混凝土浇注后的时间变量，s；x、y、z是相应点处的坐标，m；λ是混凝土导热系数，W/(m·℃)；Q(t)是单位体积混凝土水化反应累积产生的热量，J/g.

国内外提出多种形式的水泥水化热模型. 朱伯芳[8]提出一种同时考虑混凝土龄期、温度和水化度影响且计算简便的水泥水化反应放热模型，并给出根据实验资料决定计算参数的方法，以及根据工程实测温度进行反分析以求出计算参数的方法. 许朴等[9]从水泥水化放热反应本质出发，考虑龄期、温度和温度历史影响，提出一种基于水泥水化度的水泥水化反应放热模型. 凌道盛等[10]基于化学反应动力学原理,提出一种物理意义明确,考虑温度和化学反应物浓度对化学反应速率影响的水泥水化反应放热模型. Ilc等[11]通过绝热温升试验曲线和人工神经网络方法提出一个新的数值模型来预测早龄期混凝土结构的温度发展. 然而，现有水化热模型研究较少考虑前期水泥水化反应缓慢的诱导期，导致在前期对绝热温升数据的拟合误差较大.

水泥水化可以概括为水泥中各个矿物相的溶解与水化产物的沉淀过程，即溶解- 沉淀过程. 典型的水化放热曲线可以分为诱导前期(Ⅰ)、诱导期(Ⅱ)、加速期(Ⅲ)与衰退期 (Ⅳ)[12]. 在诱导前期(Ⅰ)，水泥与水拌合后的几十分钟内，水泥水化放热速率高. 这部分热量主要是由于各个水泥矿物相的快速溶解所贡献. 在诱导期(Ⅱ)，缓慢溶解理论认为，水泥矿物溶解后液相离子浓度提高，降低了水泥熟料矿物的欠饱和度，溶解速率降低[13]. 所以在短暂的高放热速率后，水泥水化放热速率显著降低，进入长达几个小时的诱导期. 在加速期(Ⅲ)，水化放热曲线显著升高；在衰退期 (Ⅳ)，由于水泥矿物表面被水化产物完全覆盖，限制了水泥矿物的溶解，故水化反应减慢. 由此可知，水泥水化过程大致经历水化速率由慢到快再变慢最终稳定的过程，其水化速率变化情况符合S形公式表达的水化放热模型. 该水化热模型便于数学运算，且在前期绝热温升的拟合中误差较小，适用于所有的大尺寸混凝土构件公式为

Q(t)=Q∞me-n/t

(2)

式中：Q∞是水泥最终水化放热量，W/m；m、n是通过试验数据由最小二乘法拟合得到的参数.

为求解热传导方程,除了确定水泥水化热模型外，还需要确定边界条件和初始条件. 所有到达边界表面的热量都通过符合第三类边界条件的对流来散热，计算公式为[14]

(3)

式中：Te是环境温度，℃；Tc是混凝土表面温度，℃；h是表面对流换热系数，W/(m2·K). 表面对流换热热系数h与结构周边流体的物理性质和流速、接触表面的形状和面积等密切相关.

混凝土浇筑时，表面附有模板，拆模后，表面经常采用保温层辅助养护. 对此2种情况，仍视为第三类边界条件，并通过等效对流换热系数来考虑模板或保温层对混凝土温度的影响，等效对流换热系数值代算公式为[15]

(4)

式中：h0是无覆盖层对流换热系数，W/(m2·℃)；δ为覆盖层厚度，m；λp为覆盖层导热系数，W/(m·℃).

由于式(1)～(4)中的所有参数都已经确定，运用Fortran语言进行ABAQUS有限元软件子程序的二次开发[16]，通过定义用户定义的材料属性(子程序UMATHT)和边界条件(子程序FILM)来完成.

2 数值模拟

2.1 模型建立

本文中2个混凝土构件A和B，尺寸为1.5 m×1.2 m×4.0 m，浇筑在预先浇筑完成的尺寸为11.0 m×10.8 m×1.0 m的混凝土承台上. 在建模工程中建立2种混凝土材料属性，一种属性赋予混凝土构件A和B，通过子程序UMATHT自定义生热、导热系数和比热容等变化参数，另一种属性赋予承台，通过ABAQUS定义混凝土硬化后的常数参数. 在有限元模型中，混凝土采用DC3D8固体传热单元，钢筋采用DC1D2单元. 在有限元分析软件ABAQUS中，环境温度Te和对流换热系数h是模拟混凝土温度场的2个重要因素. 该模型一共有4种表面，即顶面、四周表面、承台表面和承台底面. 试件的有限元模型和表面名称如图1所示.

需要说明的是，养护期和非养护期构件顶面以及脱模前后四周表面的对流换热系数是变化的，这是影响构件降温的重要因素，同时对于承台底面，仍视为第三类边界条件，将土壤视作保温层，并通过等效对流换热系数来考虑其对混凝土温度的影响，各边界对流换热系数列于表1.

表1 有限元模型边界条件

2.2 模型建立

为了更加精确地模拟构件的温度场，本文对混凝土的绝热温升和早龄期热学性能: 比热容c和导热系数λ进行试验[17]，并将实测数据用于构件的温度场模拟中.

2.2.1 绝热温升试验

绝热温升试验采用中国建筑科学研究院研制的混凝土绝热温升仪(型号BY- ATC/JR)进行测试，精度为0.02 ℃，在试件初始温度为26.01 ℃的条件下，110 h内绝热温升为47.85 ℃. 测试曲线如图2所示，对绝热温升试验数据进行拟合可得到水化热模型中的参数m和n的值分别为1.2和5.

2.2.2 导热系数λ和比热容c

为研究混凝土的早龄期热学性能随龄期的变化，对混凝土在龄期分别为1、2、3、5、7、10、14、20、28、45、60、90、120 d的c和λ进行试验，试验结果分别如图3、4所示.

试验表明c和λ在前7 d随龄期变化较大，这是因为混凝土在这期间迅速水化而导致混凝土内部各组成成分的比例差异显著. 因此将这7 d的c和λ试验数据写进ABAQUS二次开发的子程序中. 混凝土龄期在7 d之后，λ相近，在子程序中取为常数1.54 W/(m·℃)，而c随着龄期接近线性增加至60 d，最后达到0.974 kJ/(kg·℃).

3 温度场实测试验

3.1 构件设计

试验用水泥为普通硅酸盐水泥(型号P.O 42.5)；石子为碎石灰石，粒径5～20 mm；砂子为天然中砂；水为普通自来水；减水剂为聚羧酸高性能减水剂(型号EPS)，矿粉为三和天龙产的矿粉(型号S95). 按GB/T50081(2002)进行混凝土抗压强度试验[18]，28 d抗压强度为62.1 MPa. 水胶比为0.31.

为了研究构件的温度场，预先浇筑1个尺寸为11.0 m×10.8 m×1.0 m混凝土承台，以提供与实际情况类似的固定约束和温度边界。在混凝土承台上采用表2中混凝土配合比浇筑2个混凝土构件A和B，尺寸皆为1.5 m×1.2 m×4.0 m，见图5. 使用λ为0.16 W/(m·℃)的18 mm厚胶合板作为模板. 构件表面采用棉毡覆盖并蓄水养护，在混凝土浇筑120 h后拆模，停止养护.

表2 混凝土配合比

3.2 测点布置

构件内部分别布置3个测点，编号从A1～A3和B1～B3，分别布在构件中心、中间层的边缘以及底层的中心. 温度传感器采用PT100，分别用铁丝绑扎在钢筋上,见图6. 底层和边缘的测点均距构件表面50 mm. 同时，将1个PT100温度传感器(编号为0)置于环境温度下采集环境温度数据，数据用于有限元分析中，使有限元模型边界条件更加符合实际情况.

3.3 数据采集

浇筑构件时混凝土的入模平均温度为30 ℃. 浇筑后即开始采集混凝土构件内部温度数据，数据采集仪采用扬州晶明静态电阻应变仪，采集间隔周期为1 h，持续384 h.

4 数值模拟与试验结果对比分析

4.1 试验结果分析

构件A、B内部测点的温度随时间的变化曲线见图7. 在混凝土浇筑完成后，构件A和构件B所有测点的温度变化曲线均表现出明显的共同趋势，混凝土内部温度的发展大致可以分为3个阶段. 第1阶段为升温阶段，大约持续22 h，温度快速上升，试件A、B的最高温度分别为84.24、85.32 ℃，最大温升为55.32 ℃. 第2阶段为降温阶段，大致持续170 h. 在此阶段，水泥水化放热已进入减速阶段并渐渐趋于平稳，由于表面与环境对流换热，温度开始下降，最大降温速度为1.57 ℃/h. 第3阶段为稳定阶段，发生在混凝土浇筑完成的192 h以后，内外温度趋于一致，表面测点温度随环境温度变化产生波动.

4.2 数值模拟与试验数据对比分析

取构件A中的3个典型测点进行分析，即中心点A1、中间层边缘的点A2、底层的中心点A3的试验与有限元计算的温度历程曲线对比分别如图8(a)(b)(c)所示. A1、A2、A3三个测点的试验数据和有限元计算结果之间具有相同的温度历程趋势，吻合良好.

各测点温度峰值以及最终温度的有限元计算结果和试验结果对比见表3. 根据表3可知有限元计算结果和试验结果的差异在误差允许范围之内，所提出的S形水化热模型可以较好地预测大尺寸混凝土构件硬化期水化热温度场.

5 参数分析

拆模时间是大尺寸混凝土构件施工中的一个重要因素，拆除模板时间早不但可以节省时间和成本而且还可以加快施工进度. 然而，不适当的拆模时间会使得大尺寸混凝土构件更容易受到温度、湿度、气流等环境因素的影响，而这些是影响混凝土内温度梯度和裂缝演化的关键因素.

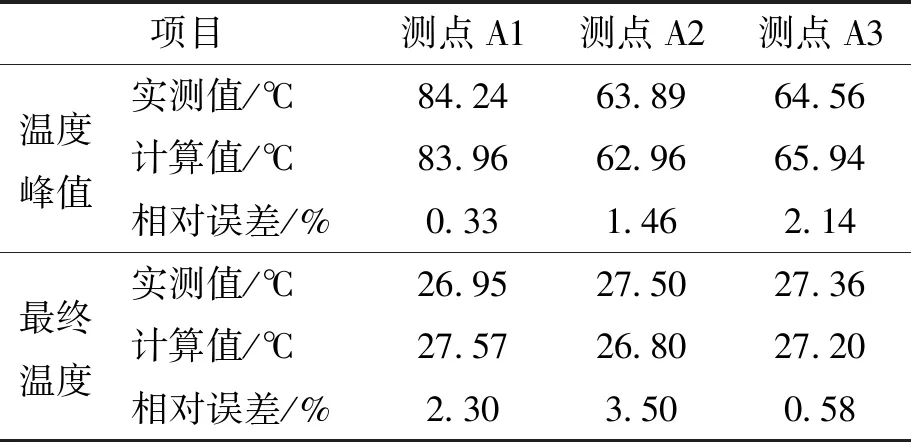
表3 温度场计算值与实测值的比较

为进一步研究拆模时间对大尺寸混凝土构件降温阶段的降温速率的影响，采用本文模型选取拆模时间在混凝土浇筑后72、96、120、144 h进行有限元分析. 测点A1在不同拆模时间的温度历程曲线见图9(a)，4种不同拆模时间的拆模后最大降温速率分别为11.993、8.53、7.36、6.05 ℃/d，见图9(b). 由图9(b)可知，拆模后最大降温速率随着拆模时间的加长而减小，适当延长拆模时间降低了大尺寸混凝土构件温度裂缝出现的风险.

6 结论

1) 基于水泥水化反应特征，提出S形水化热模型，并通过绝热温升试验数据拟合得到参数m=1.2，n=5.

2) 数值模拟结果与试验数据对比分析表明，计算结果与试验数据吻合较好. S形水化热模型形式简单，便于编制计算程序，利于简化大尺寸混凝土构件温度场的有限元仿真模拟.

3) 本文建立的模型能较精确地预测硬化期大尺寸混凝土构件的水化热温度场，为大尺寸混凝土构件考虑水化热温度影响的收缩徐变分析提供了依据.

4) 拆模后最大降温速率随着拆模时间的加长而减小，适当延长拆模时间可以降低大尺寸混凝土构件温度裂缝出现的风险.