基于乘波前体的2元TBCC变几何进气道一体化设计
2020-01-14俞宗汉谢业平黄国平蒲永彬王瑞琳
俞宗汉,谢业平,黄国平,蒲永彬,李 乾,王瑞琳
(1.南京航空航天大学能源与动力学院,南京210016;2.中国航发沈阳发动机研究所,沈阳110015)
0 引言
随着世界航天领域的军事竞争日益激烈,对飞行器装备的要求也不断提高。结合各类发动机在不同飞行条件下具有的优势,组合式动力推进系统(如TBCC、RBCC)的概念被提出,该动力系统能够使飞行器实现从地面起飞到高速巡航的动力衔接[1]。其中,基于TBCC组合动力系统具有单位比冲大、经济性好、可循环使用等特点,成为航空领域重点发展方向[2-6]。
变几何进气道的设计方法是实现TBCC宽马赫数飞行的关键技术之一[7]。通过对进气道前体的波系和通道内分流板角度的调整,实现飞行包线内各状态下的最优气动性能。与3维内转式进气道相比,2元进气道的内部构型和调节机理简单,其通道密封性更易保证,是实现变几何进气道设计的可靠途径,受到国内外学者的重视。文献[8-11]针对ATREX 2元进气道,通过调节压缩楔板来实现进气流量和波系的调整,具有流动特征简单、变几何调节难度低的特点,但该进气道第2级斜板的调节会对喉道面积产生明显影响,从而限制了变几何调节裕度;文献[12-13]针对X-43B进气道,通过增加调节自由度来提升其内流性能,使飞行器在马赫数为4.0~7.0下具有较好的性能;文献[14-15]针对内并联式TBCC动力方案,通过调节TBCC内部的分流板改变在不同工作状态下各通道的流量,完成在2.0~5.0倍声速飞行条件下的模态转换;文献[16]提出1种2元内并联式TBCC进气道结构,在大部分工况下总体性能较好,并且流场质量和出口参数也表现良好;文献[17]提出1种内并联式TBCC方案,分析了变几何泄流腔及其设计参数对进气道内部流场特性的影响。综合以上2元TBCC变几何进气道的研究可知,其内外流场以及内并联TBCC的2个流道的流场具有高度耦合的特性,是TBCC飞发一体化设计需解决的主要问题之一。总偏转角和进气道外唇口角度是2元混压式进气道的2个关键参数。总偏转角影响进气道内外压缩段的压缩效率,从而影响进气道的低马赫数起动性能;而唇口角影响飞行器的整体力矩平衡和所受外部阻力。
本文基于1种推进系统综合推阻性能分析方法,设计了1种2元混压式TBCC进气道,并对马赫数为2.0~4.0的单通道性能进行计算分析;并对过渡模态下的双通道模型进行气动计算,分析了不同开度下的进气道性能变化。
1 2元进气道及其变几何方案设计
1.1 进气道气动构型
2元混压式TBCC进气道外压缩段由按等波强原理配置的3级斜激波组成。设计飞行高度为24 km,设计马赫数为 4,其他马赫数(Ma=3.5、3.0、2.5、2.0)的飞行条件根据等动载原则得到。结合基于多级锥导乘波体设计的前体型面,利用高速巡航飞行器综合推阻分析方法(如图1所示)[18],得到最佳的2元进气道几何参数(总偏转角为23°,唇口角度为10°),设计了2元混压式进气道的气动构型,如图2所示。
1.2 进气道数值模拟
本文对设计的前体/进气道气动造型进行结构化网格划分与边界条件设置,如图3所示。近壁面的y+=30,第1层网格约为0.1 mm,网格总数约为300万。
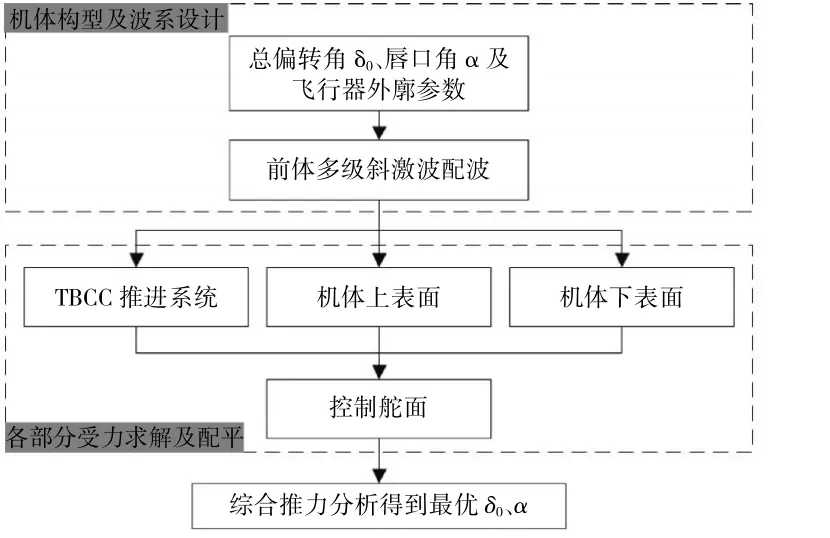
图1 推进系统综合推阻分析方法
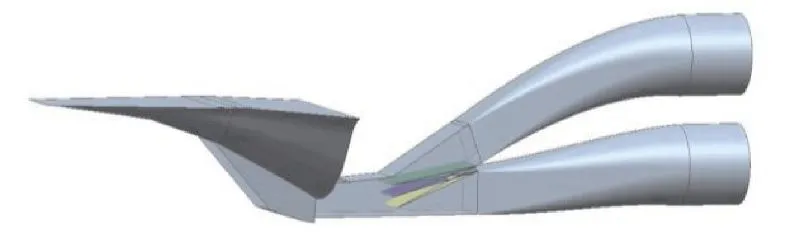
图2 一体化2元TBCC变几何进气道完整造型
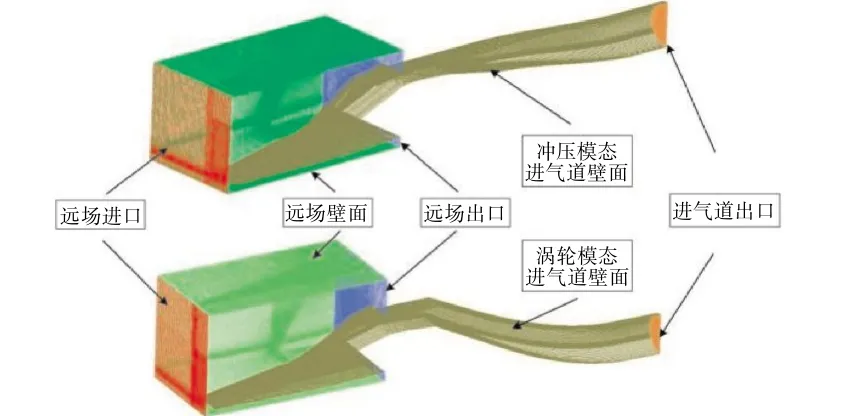
图3 带前体的2元TBCC进气道网格拓扑结构
采用商业软件CFX进行数值模拟。采用标准ke湍流模型、标准壁面函数,其校验应用与文献[19]中相同的造型。沿程压力结果分析如图4所示。从图中可见,数值仿真结果与试验结果吻合度较高,所以标准k-e湍流模型可以用于本文2元TBCC进气道的模拟验证。
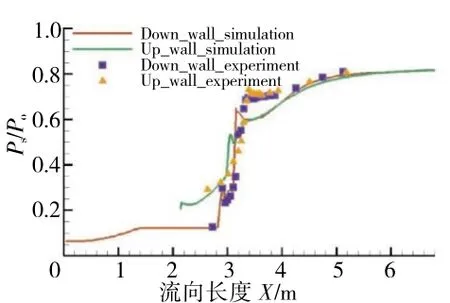
图4 沿程压力分布CFD结果与试验结果的对比
2 进气道模态转换变几何调节规律

图5 基于进气道喉道高度h与马赫数Ma的变几何结构调节规律
进气道喉道高度h随飞行速度变化的调节规律如图5所示。当飞行马赫数低于转级马赫数时,TBCC处于涡喷工作模态,所有流量都流入涡轮通道;当飞行马赫数高于转级马赫数时,TBCC处于过渡态模态,气流分别流向涡轮流路和冲压流路,通过调节分流板来改变2路的流量比,从而实现模态转换。本文选择的转级马赫数为2.5,即在马赫数为0~2.5时,进气道为涡轮工作模态;在马赫数为2.5~4.0时,进气道为冲压工作模态;在马赫数为2.5时,完成模态转换。对应的变几何机构包括转动压缩板、转动伸缩板、弧形转动板、圆弧滑动板和喉道水平板。当飞行状态变化时,通过调节可调机构改变喉道面积,从而满足飞行状态的改变,确保进气道具有最好的性能。
3 单通道性能分析
马赫数为2.0~4.0时进气道典型飞行状态数值仿真结果如图6所示。从图中可见,在设计状态马赫数为4.0时,3道入射激波与设计相符,贴口状态均较好,仅有少量溢流,流量捕获性能较高。马赫数为3.5、3.0时,来流速度减小,激波脱离唇口向外侧移动,可见唇口的溢流随马赫数的降低而逐渐增加。当来流速度处于转级马赫数2.5时,2个通道同时工作,虽然溢流量比马赫数为3.0时的增大,但是由于双通道以及喉道的放大保证了进气道的通流能力,所以溢流的增加比例小于冲压工作模态时马赫数减小的溢流变化比例。当马赫数为2.0左右时,TBCC进入涡轮工作模态,流量捕获能力相对降低,由于进气道激波强度的减小,进气道的总压损失也相应减小。

图6 各来流马赫数下对称面的速度及总压恢复系数
进气道的各项气动性能随马赫数的分布如图7所示。从图中可见,在冲压工作模态下,随着飞行马赫数的提高,进气道入射激波的强度增加,进气道唇口溢流量减小,所以流量系数增大,压比增大,出口马赫数降低,总压损失增大。当进气道来流马赫数达到4.0时,其对应流量系数为0.92,此时冲压通道出口马赫数达到0.27时,可以满足该通路的来流气体进口速度要求,且在进气道出口的平均总压恢复系数为0.47。当马赫数高于2.5时,进气道为涡轮工作模态,最大流量系数可达0.65;由于进气道入射激波的强度降低,所以相对于冲压工作模态,涡轮通道出口截面的平均总压恢复系数大于0.75。总之,数值模拟结果表明:在工作马赫数为2.0~4.0时,变几何进气道均能成功起动,流量系数在0.60以上,进气道总压恢复系数为0.47~0.85,气动性能良好。
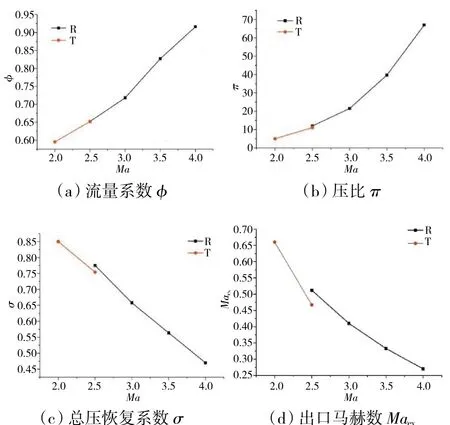
图7 进气道各性能随马赫数的分布
4 双通道性能分析
对于过渡模态下的气动分析,选择3个不同的分流板位置,形成3个定几何构型,并对双通道模型进行结构性网格划分(如图8所示),对壁面网格加密,边界层高度为0.1 mm,以保证y+≈30,网格总量为350万。选用标准k-e湍流模型和标准壁面函数进行计算。
3个不同开度下通流状态的流场结构如图9所示。在开度为1时,涡轮通道流量约为冲压通道流量的30%,分流段前气流的最大速度为马赫数1.6,经过分流段后,冲压通道内气流最大速度为马赫数2.6,涡轮通道内气流最大速度为马赫数3.4;由于分流板的开度不会影响到分流段前的气流流场分布,因此在开度2和开度3下,分流段前的气流最大马赫数约为1.6。此外,在开度2下,冲压通道与涡轮通道的流量相当,2个通道扩张程度基本一致,因此2个通道内最高马赫数约为2.7;在开度3下,冲压通道流量仅为涡轮通道的35%,经过分流段加速后,冲压通道内最大速度为马赫数3.3,涡轮通道内最大速度为马赫数2.3。
若分别在冲压通道与涡轮通道出口处施加一定的反压,使得2个通道内的结尾激波运动至分流板前缘位置处(如图10所示),此时分流段前的气流仍为超声速,2个通道之间互不干涉,进气道性能最佳。

图9 来流Ma=2.5时不同开度下通流状态流场结构
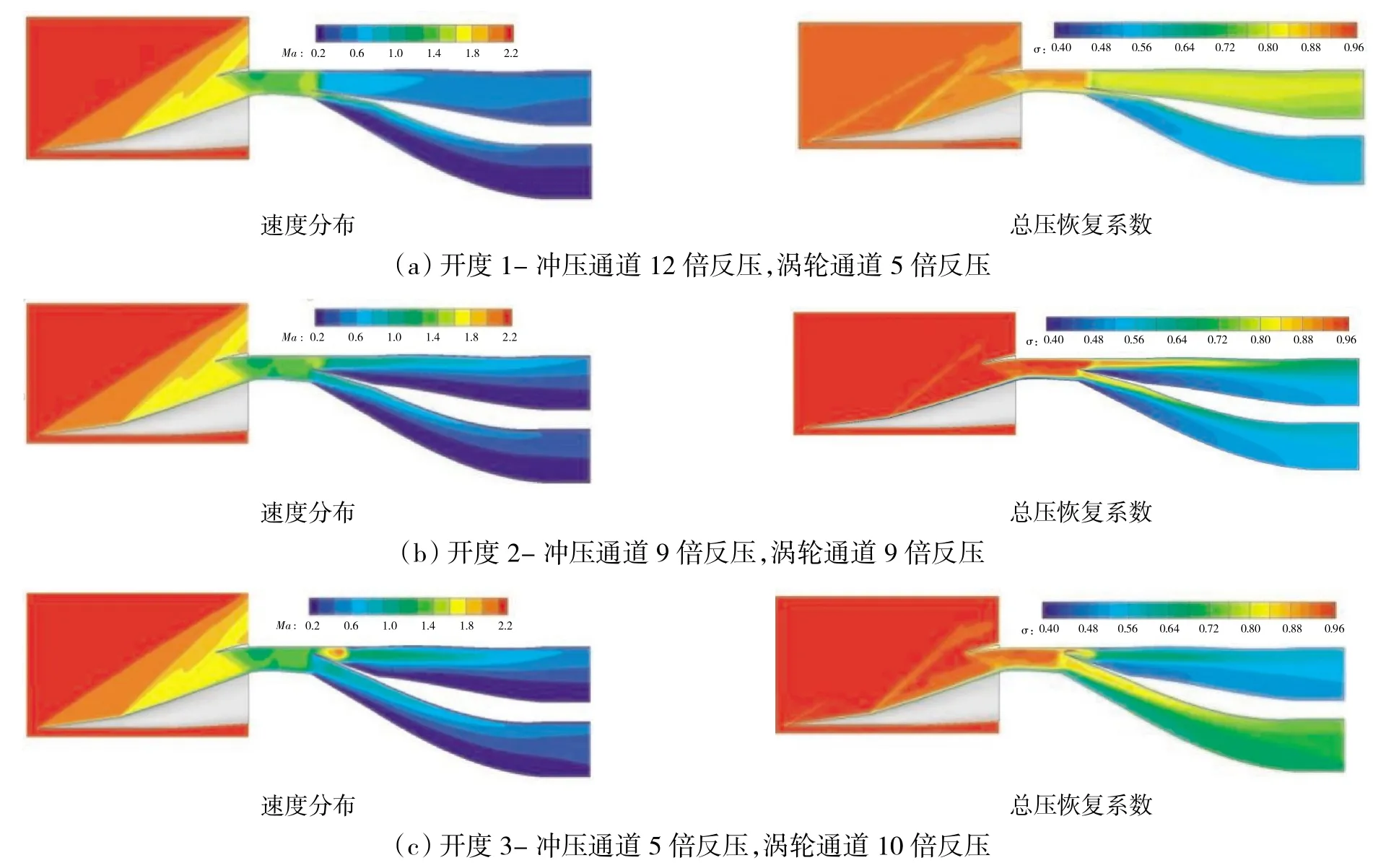
图10 来流速度为Ma=2.5时不同开度下冲压和涡轮通道的反压特性
从图中可见,在开度1下,当冲压通道出口反压为来流压力的12倍,涡轮通道出口反压为来流压力的5倍时,2个通道内的结尾激波运动至分流板前缘,此时冲压通道出口平均马赫数为0.333,涡轮通道出口平均马赫数为0.287;在开度2下,当双通道出口压力为来流压力的9倍时达到此状态,冲压通道出口平均马赫数为0.370,涡轮通道出口平均马赫数为0.270;在开度3下,在冲压通道出口施加5倍反压,涡轮通道出口施加10倍反压,结尾激波位于各自通道内,未进入扩张段,此时冲压通道出口平均马赫数为0.364,涡轮通道出口平均马赫数为0.362。流量大的通道往往具有承受更大出口反压的能力。
不同的分流板开度对应着不同的通道流量分配,将冲压通道流量与涡轮通道流量的比值定义为流量比,得到了不同流量比下2个通道的流量系数与总压恢复系数的变化规律,如图11所示。一般情况下,流量较大的通道出口气动性能参数优越,性能更好。总体上随着冲压通道流量的增加,从流量系数和总压恢复系数来看,冲压通道的气动性能逐渐转好,而涡轮通道的气动性能逐渐变差。此外,当冲压通道流量小于涡轮通道流量时,相较于流量比大于1的情况,冲压通道的气动性能对流量变化更为敏感。
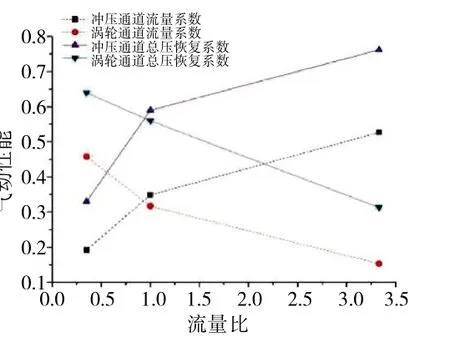
图11 过渡模态(Ma=2.5)气动性能随流量比的变化规律
5 结论
本文设计了1种基于乘波前体的2元TBCC变几何进气道,并进行了相关工作状态的数值模拟与分析计算,得到的主要结论如下:
(1)通过对飞行器受力及总压损失的综合推阻分析,得到在最小总压损失前提下净推力最大的2元进气道关键参数:总偏转角δ0=23°及唇口角度α=10°,设计了2元TBCC变几何进气道;
(2)对2元TBCC进气道的数值模拟结果表明,在工作马赫数为2.0~4.0时,变几何进气道均能成功起动,流量系数为0.60以上,进气道的总压恢复系数为0.47~0.85,气动性能良好;
(3)在过渡模态下,针对不同的冲压通道和涡轮通道的流量分配方案,对双通道模型进行了计算,总结得到不同的流量分配对2元变几何进气道的气动性能影响规律。
上述结论可有效地为TBCC变几何方案应用于工程实际提供可靠的参考和依据。
