基于统计能量法的组合式金刚石圆锯片声压级研究*

2020-01-13赵佳琦张进生鞠军伟韩亚群

金刚石与磨料磨具工程 2019年6期

关键词：锯片声压级金刚石

赵佳琦, 黄波, 张进生,4, 鞠军伟, 韩亚群

(1. 山东大学机械工程学院，济南250061)

(2. 山东省石材工程技术研究中心，济南250061)

(3. 山东大学，高效洁净机械制造教育部重点实验室，济南250061)

(4. 山东大学海恩锯业研究院，山东日照 276800)

金刚石圆锯片锯切石材等硬脆材料时其高频段噪声可达110 dB以上[1]，严重影响人体健康，因此锯片噪声辐射水平预估与噪声有效治理一直是国内外相关领域重点研究并亟待解决的问题。

近年来，专家学者已对单片圆锯片的噪声结构声学进行研究并取得了一定成果。鞠军伟[2]用有限元和间接边界元法联合仿真计算金刚石圆锯片的辐射声场，仿真研究开降噪孔对金刚石圆锯声辐射特性的影响。POHL等[3]基于阻尼效应以负电容并联压电换能器应用于锯片核心，提出一种新的圆锯片减振降噪概念。KOPECKY等[4]通过直接测量噪音和圆锯片主体振动时间响应确定振动的主要频率，分析了Pilana 400-72 TFZL圆锯片的振动特性及其噪声水平。姚涛[5]采用MATLAB分析了槽参数对锯片振动特性的影响。田永军等[6]基于显式中心差分算法和边界元-有限元分析建模法，对锯片切割系统的声辐射特性进行了研究。

以上分析都是基于单个金刚石圆锯片的，对组合式圆锯片的声学研究甚少，且对圆锯片结构的声学计算都是基于单元的确定性方法，即有限元分析和边界元分析法[2-6]。但在高频段应用有限元分析法，细化的网格需要控制频率增大时的各类误差，否则高频求解时的误差较大[7]，因而确定性方法的局限性十分明显。而统计能量分析(statistical energy analysis，SEA)方法从统计的观点抽取被研究对象[8]，以能量为独立的动力学变量，使用能量—功率流平衡方程描述圆锯片子结构间的相互作用关系[9]，统一处理圆锯片基体结构和声场的耦合动力学问题[10]，从而表现锯片机械振动与其对应的声场特性的联系[11]，适用于高频声振系统噪声的统计。

本研究中，将SEA方法引入石材切割系统噪声辐射水平数值分析过程中，建立一种组合式金刚石圆锯片的SEA模型，综合考虑系统实际工程中的模态密度、内损耗因子、耦合损耗因子、约束、激励及辐射区等条件，对组合圆锯片噪声辐射水平进行频域历程的定量估计和分析。通过数值预估值与现场实测结果比较，确定所建立的统计能量分析模型对锯片高频噪声计算的可信性。

1 组合式金刚石圆锯片SEA参数确定

组合式金刚石圆锯片是指多片2种以上规格的锯片装配在同一主轴上锯切板材的一种工具，其在控制锯片振动、减小锯缝宽度上有较大优势，在花岗石或大理石板材的切割中应用广泛，因此对组合式金刚石圆锯片的噪声进行分析具有重要的现实意义。组合式金刚石圆锯片锯切图如图1所示，其侧面示意图如图2所示。

在进行SEA方法分析时，一些“能量存储”和“能量转移”参数的设置极为重要，包括模态密度、内损耗因子和耦合损耗因子等。这些都是要研究的金刚石圆锯片子系统的几何、材料和介质特性参数[12]。因此，是基于金刚石圆锯片的结构特性来进行分析的[13]。

图1 组合式金刚石圆锯片锯切图

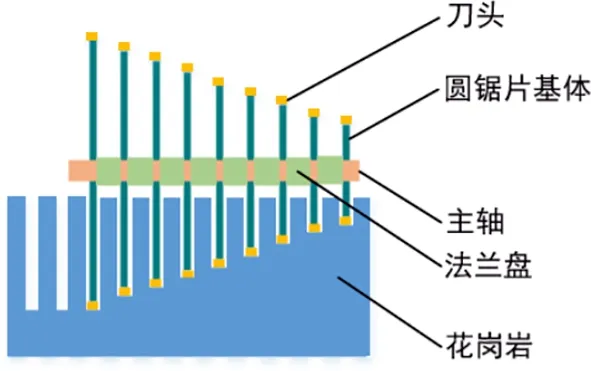
图2 组合式金刚石圆锯片侧面示意图

模态密度用来衡量金刚石圆锯片振动系统储存能量的能力[14]，组合式金刚石圆锯片模态密度的大小决定其是否适用于SEA方法。

系统的频率方程为[14]：

(1)

式中：m1，m2为正整数；KB为波数；R为平板截面回转半径；Cl为波速。

用赫兹频率f表示二维平板的模态密度[14]：

(2)

式中：n(f)为模态密度，Ap为平板表面积。

由式(2)可知：平板表面积越大，模态密度越大。

用来研究的组合式金刚石圆锯片直径D=200～3 582 mm，厚度h=1.6～11.0 mm，属于径厚比较大的磨具。在噪声的高频段分析中，将此结构划分为耦合的子系统，以单一的能量来描述不同动力学子系统的状态，从而预测各个子系统的相应声压级[6]，较之随频率增大各类误差不断增大的有限元分析法更可靠且效率更高。因此，锯片结构适合用统计能量分析方法来进行分析。

内损耗因子表示子系统对流入该子系统的能量的局部耗散能力[14]，子系统结构的内损耗因子(DLF)η通常表示为：

η=ηs+ηr+ηb

(3)

式中：ηs、ηr和ηb分别为锯片结构阻尼损耗因子、锯片振动声辐射损耗因子和锯片边界连接阻尼损耗因子。由经验数据库得到钢的结构阻尼损耗因子取3×10-4[15]。

在实际加工的高频阶段，当子系统间为刚性连接时，ηb远小于ηs，ηb可以忽略，则η可表示为下式：

η=ηs+ηr

(4)

在高频区域中，η的影响因素以ηs为主，故金刚石圆锯片振动中η由ηs决定，取η=3×10-4[15]。

耦合损耗因子(CLF)表示子系统间耦合作用的大小[14]。线连接板结构耦合的CLF可表示为：

(5)

式中：l为连接线长度；Cg为弯曲波群速度；A1为板1面积；ω为频率；τ12为连接处传递系数，其经验公式为：

(6)

式中：D1、D2分别为2个连接板的刚度，其经验公式为：

(7)

式中：ρs为板的面密度。

因此，由式(5)～(7)可确定金刚石圆锯片子系统的耦合损耗因子。

2 组合式金刚石圆锯片声压级仿真及试验

2.1 组合式金刚石圆锯片SEA模型建立

实际生产中，锯切花岗石常用的组合式金刚石圆锯片的标准参数如表1所示。

表1 组合式圆锯片结构参数

以表1为依据，建立组合式金刚石圆锯片SEA模型，根据统计能量分析的基本假设及统计能量分析建模的简化原则[15]，不考虑主轴系统对金刚石圆锯片统计能量分析的影响，在金刚石圆锯片的中心孔施加固定约束来模拟主轴对锯片的约束。金刚石圆锯片的基体材料为75Cr1，其材料性能参数[16]如表2所示。

根据统计能量法中用于描述各种结构和声学组件响应的不同SEA子系统库，将锯片的基体结构进行子系统划分，基于表1中9片不同直径锯片划分出9个SEA子系统；板块子系统包含与弯曲、拉伸和剪切波相关的3个波场。SEA子系统中的每个波场作为振动声能的独立储存器，旨在捕捉声学子系统的动态行为，自动计算每个子系统不同波场的属性。

表2 圆锯片基体材料参数

建立的SEA声腔用来描述三维声学成分中的波传播，由节点闭合环或其他子系统表面确定。为了使声腔和与其相邻的子系统具有良好的辐射连接，通过板边界来建立该系统的声腔；同时，为模拟试验中距离组合锯2 m处测试的声压情况，建立2 m×2 m×2 m的外声腔[17]，以保证外声腔与锯片子系统间的耦合。

建立SEA半无限流体，计算一定数量的板辐射的声压级，估计声学体内的SPL。每个半无限流体由声学流体和单个三维声学节点确定，来评估辐射的声压级。

定义DLF和CLF后，将该属性赋予9个金刚石圆锯片子系统，并向模型施加载荷模拟实际工况中锯片受到的激励。轴向载荷是金刚石圆锯片噪声产生的主要原因，向SEA模型施加的轴向载荷模型为[18]：

Fx=(Fτ/r0)(∂x/∂θ)

(8)

式中：Fτ为锯切切向分力；r0为锯切力作用的半径；x为锯切力作用点处的横向振动位移；θ为锯切力作用点的位置角。

由于SEA方法只适用于高频分析，在低频处的计算误差较大，所以取1 000～8 000 Hz的高频区作为求解范围，以得到更为准确的求解结果。且计算时，锯片原结构状态周围无任何吸声或隔声材料。

2.2 组合式金刚石圆锯片的噪声仿真和试验验证

根据实际工况，对上述组合式锯片切割石材时的噪声进行检测，锯切石材噪声检测方案示意图如图3所示。

单臂式组合锯外形尺寸为5 400 mm×7 000 mm×6 900 mm，电机转速1 470 r/min，进给速度1～2 mm/min，横向进给20～30 mm/min。在测量开始前，先确定好测量位置，测量位置为距离锯片2 m处；锯片开始锯切石材后，采用SVAN971声级计测量2 min时石材锯切产生的噪声。为减小测量误差，测量10次锯切过程中的最大A声级，若10次测量结果绝对误差彼此不大于2 dB(A)，则认为测量结果有效。测量结束后，对测量结果进行算数平均，取最终平均结果为有效值。试验采用的组合式圆锯片基体规格如表1所示，基体外径460 ～1 584 mm、厚度4.0 mm的9片组合式金刚石圆锯片噪声计算结果和试验结果对比如图4所示。

图3 锯切石材噪声检测方案示意图

图4 组合式金刚石圆锯片SPL

从图4可以看出：SEA模型的计算结果与试验结果较为吻合，在频率1 000～4 000 Hz区间，噪声声压级快速上升直达峰值102.3 dB；在频率4 000～8 000 Hz区间，噪声声压级随频率增加平缓下降。从整个高频范围来看，图4中试验和仿真结果的最大误差在2 000 Hz处为1.7 dB，小于2 dB，满足工程精度要求，证明了所建立的统计能量分析模型对锯片高频噪声计算的可信性。

在锯切过程中锯片和石材发生摩擦接触并产生摩擦噪声，摩擦的界面特征是影响摩擦噪声的关键因素。由图4的试验数据可以看出：组合式金刚石圆锯片在高频区的声压级范围为88.3～102.3 dB，且随频率增大呈先上升到一定峰值后再平缓下降的趋势，在频率为4 000 Hz处达到峰值102.3 dB。

锯切系统的振动和锯切物料的摩擦噪声是锯切过程中的主要噪声源。组合锯在锯切过程中产生大量锯屑，这些锯屑在摩擦界面无法及时排出并不断被碾压、碎化，会形成锯屑堆积的磨屑层，磨屑层不断堆积和剥落造成切削表面的凸起和深坑；同时，锯屑在锯缝中的不断堆积，产生了较高的摩擦系数。锯切接触表面不平、锯屑堆积的磨屑层的不均匀分布以及锯切作用，使锯切相对速度发生变化，导致锯切过程中的界面摩擦力剧烈波动，发生大小突变，在频率4 000Hz附近形成摩擦力高频成分；在冲击力作用下，锯切系统多模态同时被激励，振动强度各不相同，破坏了其状态变量的连续性，其响应组合引起锯切系统强烈的自激振动并产生高声压级噪声。

3 组合式金刚石圆锯片声压级的影响因素

3.1 不同锯片组合方式的影响

为观察不同锯片数组合的组合锯仿真分析的噪声声压级影响规律，取表1中规格分别为460、600、740、880和1 020mm的圆锯片组合成表3所示的1～5片组合锯，其噪声声压级对比如图5所示。

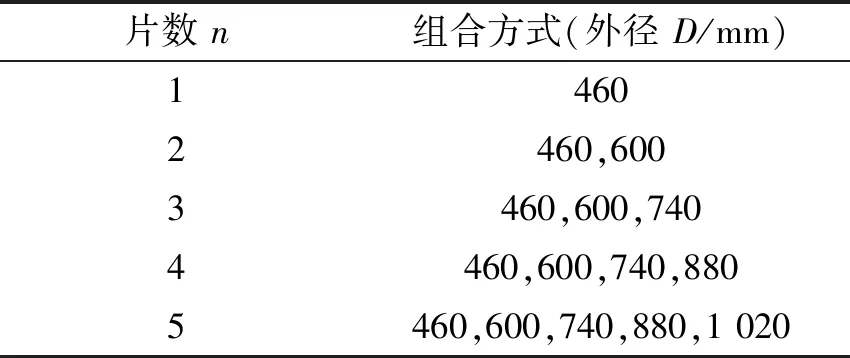
表3 不同片组合式圆锯片规格

图5 不同片数组合式金刚石圆锯片SPL对比图

由图5可以看出：不同片数组合式金刚石圆锯片的SPL变化趋势基本相同，其高频区声压级范围为79.5～99.2 dB；在频率1 000～4 000 Hz，噪声声压级快速上升直达峰值，在频率4 000～8 000 Hz，噪声声压级随频率增加平缓下降；且随片数增加，噪声声压级也呈整体递增趋势，但递增幅度随片数增加而减小。

由噪声叠加原理知：多片锯片锯切石材产生的噪声作用于某一点时产生噪声叠加，其声能量可以代数相加，但声压不可以直接叠加。总声压级可表示为[19]：

(9)

式中：LP为总声压级，LPi为不同锯片的声压级，n为组合的锯片片数。

作用于同一处的锯片声源为独立声源时，相位相同处叠加则振幅和辐射能量可直接叠加，合成的总声压级增加；如果在相位相反处叠加，理论上因为干涉原理振幅减小，声压级就会减小。组合式金刚石圆锯片在切割过程中圆锯片片数增加，刀刃到圆片的振动相对于原来的振动减弱，声波能量减小，因此其整体递增的幅度随片数增加减小。

3.2 不同基体厚度的影响

取表1中规格从460～1 584 mm 的9片组合式金刚石圆锯片为一组，其基体厚度分别为3.5、4.0、4.5和5.5 mm，不同厚度下的噪声声压级对比如图6所示。

图6 不同厚度组合式金刚石圆锯片SPL对比图

由图6可以看出：不同基体厚度的组合式金刚石圆锯片声压级变化趋势基本相同，其在高频区的声压级范围为86.1～104.7 dB；在频率1 000～4 000 Hz，噪声声压级快速上升至峰值；在频率4 000～8 000 Hz，噪声声压级随频率增加平缓下降。且随基体厚度增加，噪声声压级呈现整体递增趋势，在峰值处尤为明显。

基体厚度增加，锯屑产生速度与产生量增加，在锯缝中以更快的速度产生更厚的磨屑层，使锯切相对速度发生变化，摩擦力大小发生更强烈的突变，导致锯切系统产生更密集的振动模态变化，引起的噪声声压级进一步增大。