行人二次过街交叉口信号相序多目标优化方法
2020-01-13王艳丽卢建涛
王艳丽, 卢建涛, 吴 兵
(同济大学 道路与交通工程教育部重点实验室,上海 201804)
0 引 言
对于大型平面交叉口,行人过街长度较大,部分行人在一个绿灯信号内不能一次性过街,存在红灯时强行穿越与机动车相互干扰的隐患,不仅降低了交叉口的通行能力,也增加了交通事故风险。此类交叉口,在人行横道中央设置安全岛的同时,还需要设置行人二次过街信号,使行人可以分2个相位完成过街,减少行人过街等待时间,提高行人过街安全和交叉口的交通效率。
当前信号交叉口,对于行人过街相位的设置,往往以机动车延误最小为目标进行配时,行人相位通常与同方向的直行机动车相位一致。也有学者对行人相位的优化研究,如行人清空信号的设置[1]、行人专用相位的设置[2],以及行人相位配时方法[3]等。具体到行人二次过街,不少学者对二次过街的适用性和相位的设计进行了研究[4-6],结果显示二次过街可以有效减少机动车和行人延误。但这些研究虽然给出了相位的设计方法(主要是基于相位叠加组合),却未涉及行人相序的选择。合理的信号相序不仅能够避免和减少交织与冲突,保证信号交叉口的安全性,而且能够支持跨相位的变化,能够较少损失时间,充分利用交叉口的时空资源。目前,已有的相序优化研究大多集中于设置和调整机动车相序[7-8],以机动车的延误最小为目标,也有考虑交叉口的混合交通流特征以相位损失时间最小为目标的相位相序优化模型[9]。但信号相序的优化应综合考虑相序对机动车和行人的影响下的综合效益。
本文以行人二次过街的定时信号控制交叉口为研究对象,考虑不同信号相序方案对交通信号控制参数的影响,权衡多个交通流运行指标,建立行人二次过街单点交叉口相序多目标优化模型,并给出了计算方法。最后,将模型运用到一个实际的四相位行人二次过街交叉口,对模型和算法进行了验证,得到行人二次过街单点交叉口多目标优化下的最优相序。
1 行人二次过街相位设计
二次过街就是通过设置安全岛将道路分成两段,使行人分两个阶段穿越道路[10]。二次过街方式能够缩短行人一次过街距离,并可相应缩短行人清空时间,配合采用二次过街信号控制增加同一周期内行人放行的时间或次数,使交通控制更加灵活、可靠,从而提高整个交叉口的通行效率和行人交通流的可控性。对于不同的机动车信号相位及配时方案,行人二次过街信号的设置有所不同。以四相位信号控制交叉口为例,设置行人二次过街组织方案有两种形式:专左相位二次过街组织方法和直左相位二次过街组织方法。
1.1 专左相位二次过街组织方法
专左信号相位通常包括南北直行、南北左转、东西直行、东西左转4个相位。如图1所示,在设置专用左转相位的交叉口,行人可以利用左转信号相位的时空资源,增加行人过街可以利用的机动车相位,从而增加行人的过街时间。如果将4条人行横道以各自的安全岛分隔为8段,则每个相位都有4段人行横道可以被行人利用。
通常专左信号相位中并未考虑右转车辆,在行人过街相位中存在行人与右转车辆相互交织。对于过街行人流量和右转车流量较大的交叉口,容易出现行人与右转车辆冲突,严重影响右转车辆的通行效率和行人过街安全。在此类交叉口,利用右转专用道,同时利用信号相位控制右转车辆,消除行人与右转车辆冲突,保障行人过街安全,提高行人过街效率。如图2所示,令右转车辆与左转车辆受同一信号相位控制,同样每个相位有4段人行横道可以被行人利用。
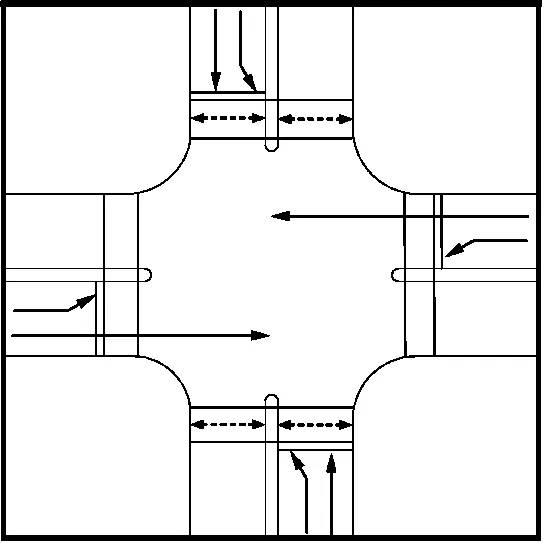


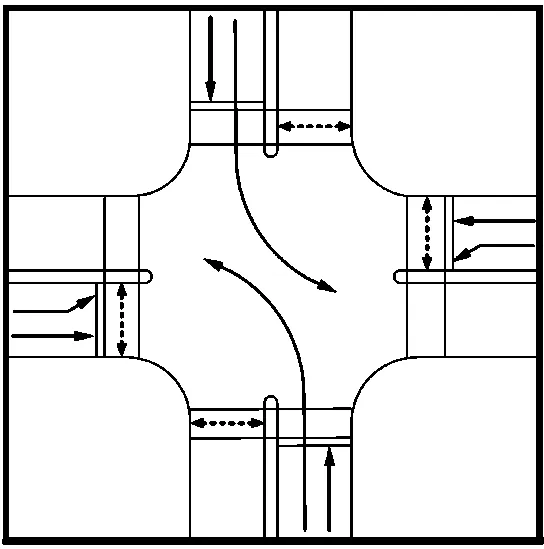
图1 专左相位二次过街
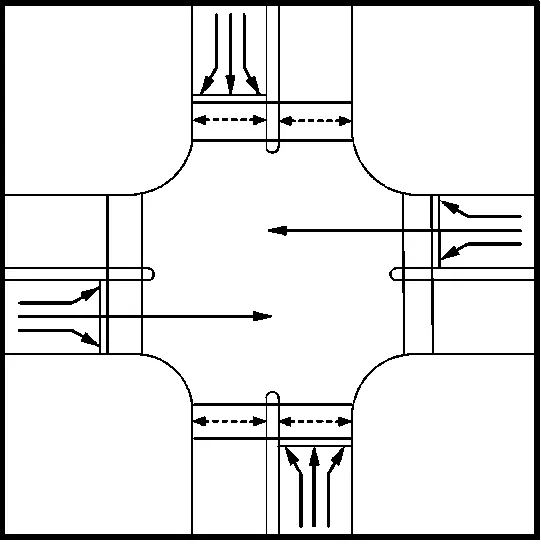



图2 专左右相位二次过街
1.2 直左相位二次过街组织方法
直左信号相位包括东进口直行左转右转、西进口直行左转右转、南进口直行左转右转、北进口直行左转右转四个相位。如图3所示,在设置直左相位的交叉口,行人可以利用各直左相位的时空资源,在机动车不穿越的人行横道过街,每个相位行人可以利用4段人行横道过街。


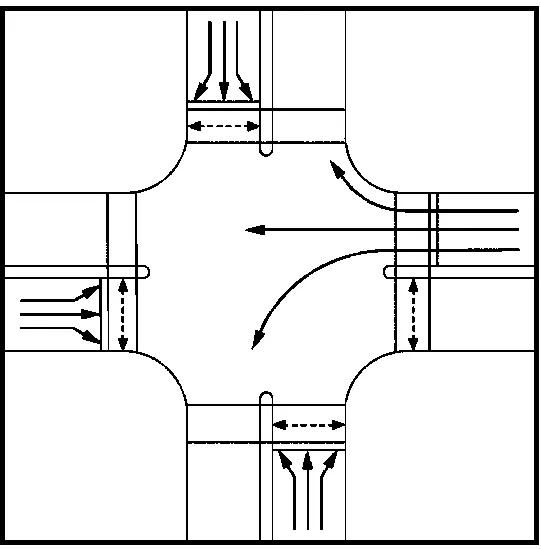
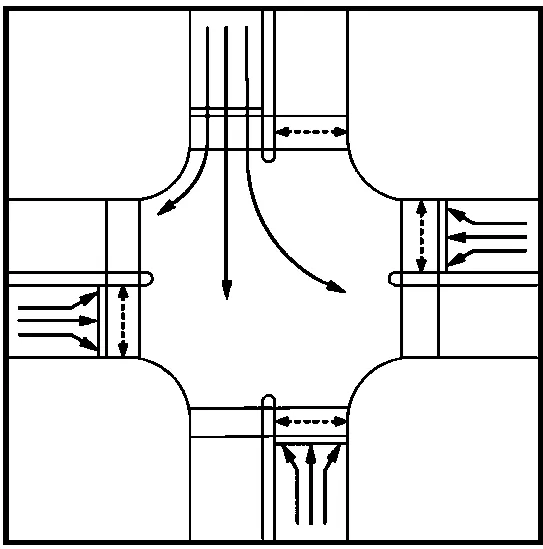
图3 直左相位二次过街
2 相序优化目标选取与计算
2.1 优化目标选取
在信号交叉口,信号相序的选择与安排对交叉口的通行效率具有重要影响。通过优化相序可提高交叉口的运行效率,进一步改善交叉口时空资源利用率。随着信号相序的改变,不同冲突交通流进入交叉口的顺序也随之改变,相应的信号控制交叉口配时参数也需要进行适当调整。
根据调查分析,信号控制交叉口配时参数将会影响到以下交通效益指标:机动车延误、非机动车延误、行人延误、机动车排队长度、机动车通行能力、机动车停车率、燃油消耗、污染物排放、噪声污染等[11]。考虑到信号相序方案对配时参数的影响,以及配时参数对交通效益的影响,选取整个交叉口信号总损失时间、机动车平均信控延误、非机动车平均信控延误和行人平均信控延误4个指标最小作为信号相序的优化目标,并给出各目标的计算方法。其中,非机动车平均信控延误的计算方法,假定非机动车与行人在交叉口受同一组信号灯控制,采用二次过街方式,所以将非机动车换算成行人,换算系数为2.0人/非机动车[12],并运用行人二次过街信号控制延误模型进行计算。
2.2 信号总损失时间
信号损失时间由启动损失时间、黄灯时长和绿灯间隔时间决定。信号总损失时间为一个信号周期内相位转换造成信号损失时间的总和[13],计算公式如下:
式中:L为信号总损失时间,s;Ls为起动损失时间,s;I为绿灯时间间隔,s;tY为黄灯时长,s;k为一个周期内的绿灯间隔数;tAR为全红时间,s,
(3)
sr为清空距离,m;l为车辆长度,m;vr为清空速度,m/s;se为进入距离,m;ve为进入速度,m/s。
2.3 机动车平均信号控制延误
由于是选择相序重新计算信号交叉口配时,无初始排队附加延误,故只考虑均匀延误、随机附加延误[13],具体公式如下:
(7)
(8)
式中:dI为交叉口车均信控延误,s·pcu-1;dA为进口道A的车均信控延误,s·pcu-1;qA为进口道A的高峰15 min的交通量,pcu·15 min-1;di为进口道A的第i车道车均信控延误,s·pcu-1;qi为进口道A的第i车道高峰15 min的交通量,pcu·15 min-1;d1为均匀延误,s·pcu-1;d2为随机附加延误,s·pcu-1;C为周期时长,s;λ为进口道A的第i车道的绿信比;T为分析时段的持续时长,h;x为进口道A的第i车道的饱和度;e为校正系数;CAP为进口道A的第i车道的通行能力,pcu·h-1。
2.4 行人二次过街信号控制延误
对于任一进口道,行人二次过街信号控制延误由第1段行人过街延误和第2段行人过街延误组成[14]。在计算时假设:①在交叉口行人均匀到达;②排队等候过街的行人一旦获得绿灯信号,即同时开始过街,无先后次序;③假设行人延误不受右转车辆影响。这里,以应用广泛的专左相位二次过街(见图1)为例给出延误计算模型。
2.4.1 第1段行人过街延误
在一个信号周期中,有2个相位是第1段行人绿灯相位,行人随机到达等待第1段行人绿灯,第1段行人过街延误可以按照一次过街延误计算[15]。根据第1段行人绿灯相位出现顺序,有2种组合情况,具体过街延误计算公式如下:
(9)
式中,dpf为第一段行人过街延误,s·per-1;rpf,1为第1段第1个行人红灯相位时长,s;rpf,2为第1段第2个行人红灯相位时长,s;t1为第1段2个行人绿灯相位开始时间的差值,s;gpf,1为第1段第1个行人绿灯相位时长,s;gpf,2为第1段第2个行人绿灯相位时长,s。
2.4.2 第2段行人过街延误
与第1段行人绿灯相位相同,在一个信号周期中,同样有两个相位是第2段行人绿灯相位。即使假设行人在第1段均匀到达,由于第1段行人信号的存在,第2段行人有2种不同的到达形式,即行人在第1段红灯或绿灯相位到达。而根据第2段行人绿灯相位顺序各有3种不同的组合情况。
(1) 行人在第1段红灯相位到达。在第1段红灯相位到达的行人需要等待下一行人绿灯相位,在下一行人绿灯相位形成1个小组通过第1段过街到达中央安全岛。这部分延误可以认为第1阶段和第2阶段相邻行人绿灯相位开始时间的差值减去行人第一段过街时间,计算公式如下:
若t1=gpf,1,
dps,r=0
(10)
若t1=gpf,1+rpf,1,
(11)
若t1=C-gpf,2,
dps,r=gpf,2-tc,1
(12)
式中:dps,r为行人在第1段红灯相位到达的第2段行人过街延误,s·per-1;tc,1第1阶段行人过街时间,s;t2为第2段两个行人绿灯相位开始时间的差值,s;gps,1为第2段第1个行人绿灯相位时长,s;gps,2为第2段第2个行人绿灯相位时长,s。
(2) 行人在第1段绿灯相位到达。在第1段绿灯相位到达的行人,因为行人并没有形成一个小组通过第1阶段过街,行人到达就开始第1阶段过街。这部分延误的计算需要根据第1阶段和第2阶段行人相位的组合,计算公式如下:
若t1=gpf,1,
(13)
若t1=gpf,1+rpf,1,
(14)
若t1=C-gpf,2,
(15)
式中:dps,g为行人在第1段绿灯相位到达的第2段行人过街延误,s·per-1。
第2段行人过街延误是两种第2段行人过街延误的加权值,计算公式如下:
(16)
式中,dps为第2段行人过街延误,s·per-1。
行人2次过街信号控制延误模型,计算公式如下:
dp=dpf+dps
(17)
式中,dp为行人二次过街信号控制延误,s·per-1。
3 相序多目标优化模型与算法
3.1 相序多目标优化模型
以混合交通流为控制对象,选取信号损失时间最小、机动车延误最小、非机动车延误最小和行人延误最小为优化目标,以最小绿灯时间为约束条件,建立行人2次过街单点交叉口相序多目标优化模型。
minf=[minL,mindv,mindp]
s.tCλj≥gmin,j
式中,gmin,j为第j相位最小绿灯时间。
3.2 优化模型的计算方法
行人二次过街单点交叉口相序多目标优化模型的计算步骤如下:①确定交叉口几何参数和信号相位方法;②选择相序方案,计算信号总损失时间;③计算该相序方案下的信号周期和各机动车相位绿灯时长;④计算该相序方案下行人信号配时方案;⑤若各显示绿灯时间满足最短绿灯时间,则转向步骤⑥,否则转向步骤③;⑥计算该相序方案下的机动车延误、非机动车延误和行人延误;⑦若全部相位枚举完全,则转向步骤⑧,否则转向步骤②;⑧利用多属性决策方法选择合适的相序方案。
3.3 多属性决策方法
由于各个方案在不同属性上的表现好坏不一,很少有某一个方案会是绝对的最优选择,因而必须确定一个决策者对属性的偏好结构,并对所有方案在各个属性上的表现进行综合评估。多属性决策方法是利用已有的决策信息通过一定的方式对一组(有限个)备选方案进行排序并择优。考虑到优化模型中多目标的特征属性,采用属性权重完全未知且属性值为实数的多属性决策方法[16],具体步骤如下:
(1) 对于某一多属性决策问题,设X={x1,x2,…,xn}为方案集,U={u1,u2,…,un}为属性集,属性权重信息完全未知。对于方案xi,按属性uj进行测度,得到xi关于uj的属性值aij,从而构成决策矩阵A=(aij)n×m(aij>0)。
(2) 属性类型主要有效益型和成本型。为了消除不同物理量纲对决策结果的影响,决策时需要对决策矩阵A进行规范化处理。
(18)
(19)
式中:I1和I2分别为效益型和成本型属性的下标集合。决策矩阵A经过规范化处理后,得到规范化矩阵R=(rij)n×m。
(3) 利用有序加权几何平均算子g对各方案xi(i∈N)属性值进行集结,求得其综合属性值zi(i∈N)。
(20)
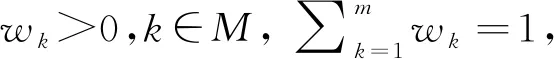
(21)
(22)
(23)
式中,i=2,…,n-1,λ,μ∈[0,1],且λ+μ≤1。
(4) 按zi(i∈N)的大小对方案进行排序并择优。
4 应用案例分析
选取上海市曹安公路-嘉松北路交叉口(见图4)进行实例验证。该交叉口为专左相位行人2次过街信号控制交叉口,右转车辆不受信号控制,该交叉口各方向的高峰小时交通流量数据见表1。现有信号方案以及可选相序方案如表2所示,利用相序多目标优化模型和算法求解最优相序。
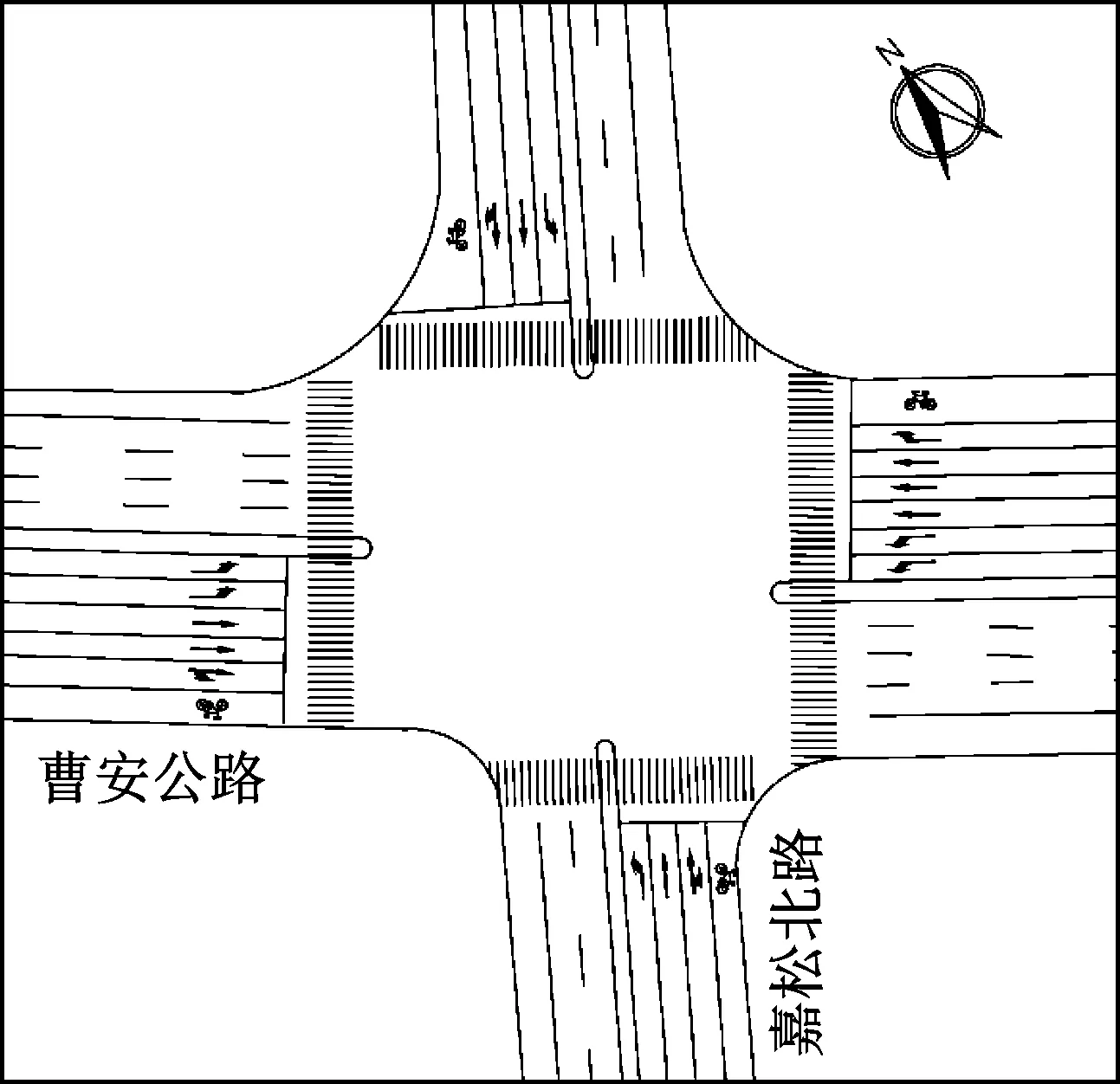
图4 交叉口布局
运用多目标优化模型进行计算,求得各相序方案的损失时间、机动车延误和行人延误,构成决策矩阵A如表3所示。对A进行规范化处理,损失时间、机动车延误和行人延误为成本性属性,得到规范化矩阵计算与有序加权几何平均算子g相关的指数加权向量,结果如下:λ=0.2,μ=0.3,w1=0.156 3,w2=0.166 7,w3=0.166 7,w4=0.151 5。利用g对各相序方案的属性值进行集结,求得其综合属性值,如表4所示。根据各相序方案的综合属性值进行排序,相序方案5为该交叉口最优相序方案。
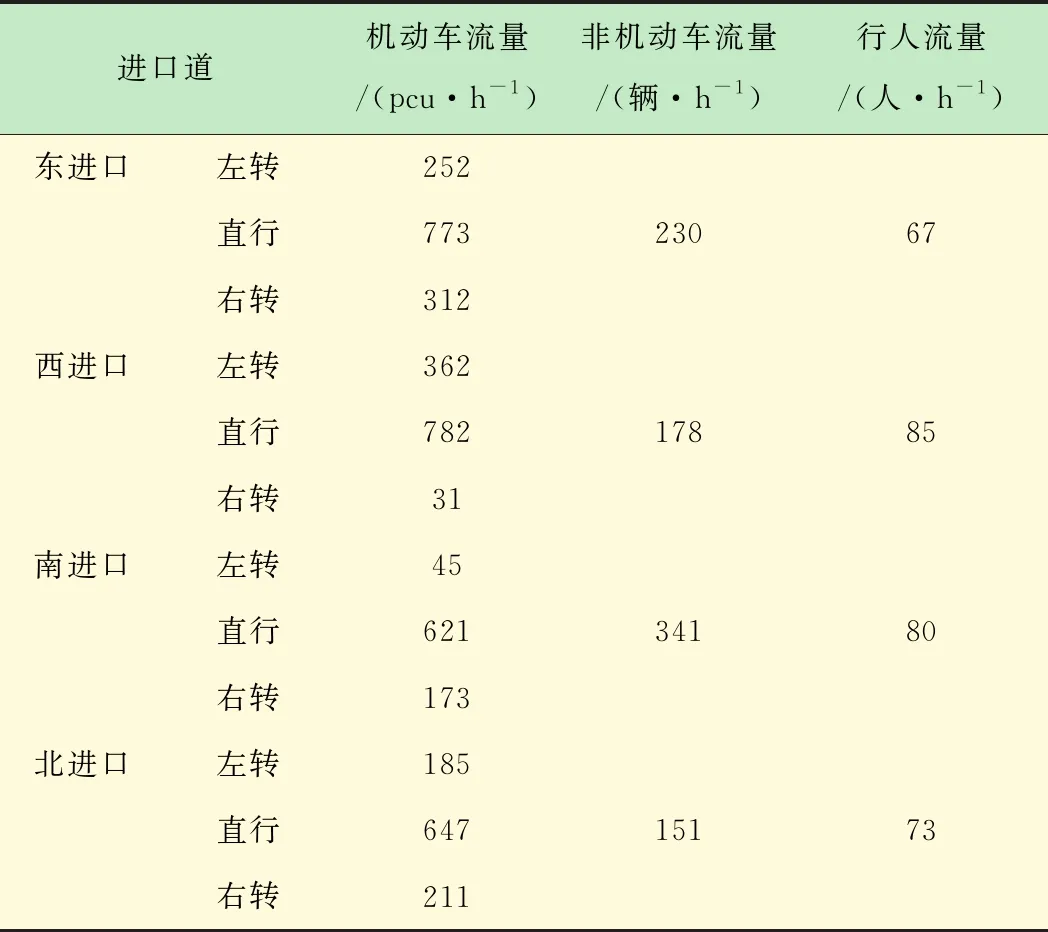
表1 曹安公路-嘉松北路交叉口高峰小时流量

表2 所有相序方案

表3 决策矩阵A计算结果

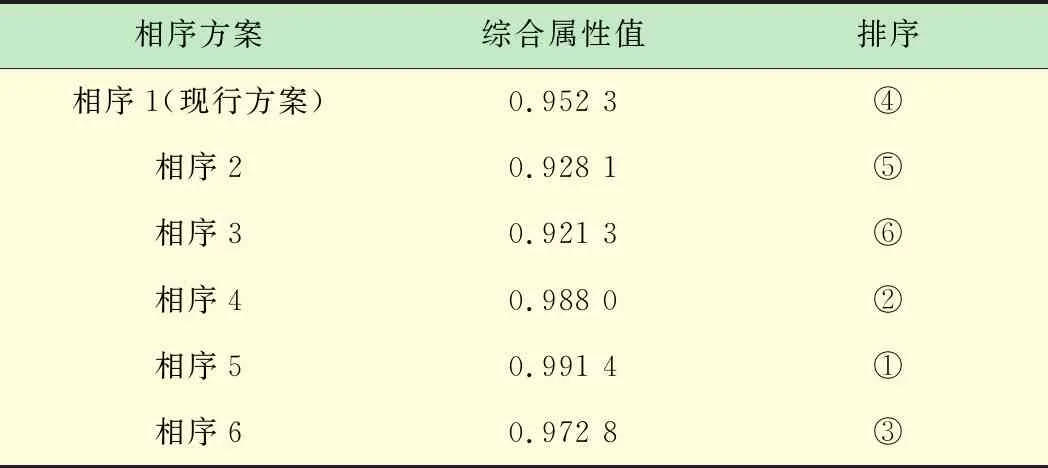
表4 综合属性值
通过计算,交叉口最优相序方案与现行交叉口相序方案相比,各交通效益指标均有一定程度的改善,损失时间减少1.86%,机动车延误减少1.43%,非机动车延误减少10.37%,行人延误减少10.43%。与交通效益最差的相序方案(相序3)相比,损失时间减少11.83%,机动车延误减少9.11%,非机动车延误减少10.74%,行人延误减少11.67%(见表5)。
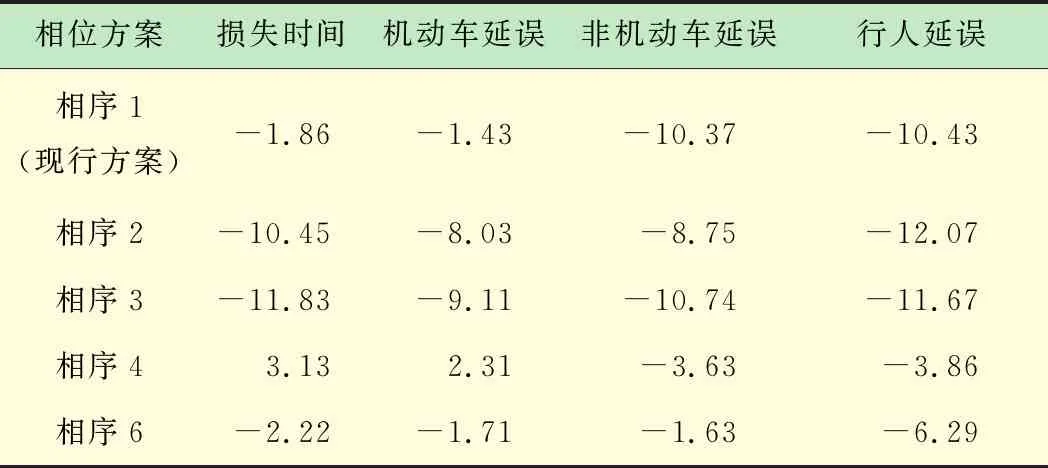
表5 最优相序(相序5)与其他相序效益值对比 %
5 结 语
针对具有混合交通流特征的行人二次过街交叉口,考虑信号相序对交叉口交通参与者的影响,选取信号总损失时间、机动车平均信控延误、非机动车平均信控延误和行人平均信控延误最小作为信号相序的优化目标,建立行人二次过街单点交叉口相序多目标优化模型。并以应用广泛的专左相位二次过街为例,建立行人二次过街平均信控延误计算方法。通过一个专左相位行人二次过街交叉口实例分析证明,相序多目标优化模型能够有效平衡多个交通流运行指标,得到综合效益最优的相序方案。行人二次过街单点交叉口相序多目标优化模型可以弥补单目标优化方法的不足,能有效权衡多个控制目标,获得更优的综合效益。考虑损失时间对信号控制交叉口配时参数的影响,后续研究中可将相序方案和信号配时同时进行优化。
