考虑尾矿材料参数空间变异性的尾矿坝稳定可靠度分析*

2020-01-13蒋水华朱明明黄劲松

中国安全生产科学技术 2019年12期

蒋水华，朱明明，黄劲松

(南昌大学建筑工程学院，江西南昌 330031)

0 引言

随着国民经济和工程技术的快速发展，我国尾矿库数量越来越多，规模越来越大。目前我国尾矿库超过了12 000座，其中95%的尾矿库采用上游法筑坝，尾矿库同时也是矿业风险的主要来源之一[1]。近年来，地震、洪水等各种原因导致我国尾矿库溃坝事故频繁发生，危害极其严重。另外，尾矿材料是性质极其复杂的地质介质，在施工过程中人为与非人为因素的作用下，其物质组成和内部结构会发生一定的变化，尾矿材料性质在空间上相差较大，即呈现一定的空间变异性。尾矿材料参数空间变异性的客观存在给尾矿坝稳定性分析带来了一定的困难，常用的确定性分析方法因不能反映这种空间变异性的影响，会导致评价结果存在一定的偏差。

目前针对尾矿坝稳定可靠度问题开展了大量有益的研究工作，如胡平安等[1]采用JC法探究了不同尾矿材料力学参数的变异性对湖北省渔潭尾矿坝可靠度的影响；刘迪等[2]利用贝叶斯网络模型建立尾矿坝稳定性因果关联分析模型，分析了各因素变化对尾矿坝稳定的影响；曹志松等[3]采用二次多项式构建响应面模型，计算了黏聚力、内摩擦角和重度服从正态分布情况下的尾矿坝稳定可靠度；张扬等[4]采用蒙特卡罗模拟(MCS)方法探讨了尾矿材料黏聚力、内摩擦角、密度等和孔隙水压力的不确定性对独木垅尾矿坝抗滑稳定的影响。虽然这些研究工作推动了可靠度理论在尾矿库安全性评价中的应用，但是大多采用随机变量模型模拟尾矿材料参数的不确定性，不能有效考虑空间不同点局部和整体尾矿材料物理力学性质的差异，无法客观地评价尾矿材料参数空间变异性对尾矿坝稳定可靠度的影响。相比之下，随机场理论将土层不同位置上的土壤参数模拟为一个服从某一概率分布的随机变量，并与相邻位置上的随机变量相关，非常适合表征尾矿材料的空间变异性，目前在边坡工程中得到了广泛应用[5-7]，但是较少应用到尾矿材料参数空间变异性表征中。此外，对于需考虑尾矿材料参数空间变异性的复杂尾矿坝稳定问题，MCS等传统可靠度分析方法的计算精度和效率欠佳，因此需要发展一种高效的考虑参数空间变异性的尾矿坝稳定可靠度分析方法。

本文结合随机场理论、代理模型和结构可靠度理论，采用考虑尾矿材料参数空间变异性尾矿坝可靠度分析的非侵入式随机有限元法，通过Karhunen-Loève(K-L)展开方法模拟尾矿材料物理力学参数空间变异性，借助Hermite随机多项式展开建立尾矿坝安全系数代理模型，在此基础上计算尾矿坝边坡稳定可靠度，并以实际尾矿坝工程为例验证了提出方法的有效性[5-7]。

1 尾矿材料参数空间变异性模拟

采用随机场模拟尾矿材料参数空间变异性时，重要的一步是进行随机场离散，本文选用计算精度和效率较高的K-L级数展开方法离散尾矿材料参数随机场。

以离散尾矿渗透系数ks与内摩擦角φ各向异性对数正态参数随机场为例，简要介绍基于K-L级数展开方法的尾矿材料参数空间变异性模拟过程。K-L展开方法离散随机场是以谱分解有界，对称且正定的相关函数为基础，将土体参数随机场的离散转化为求解Fredholm积分方程的特征值问题[6]，即

(1)

式中：(x1,y1)和(x2,y2)表示计算区域Ω中的任意2个坐标点；ρ[(x1,y1),(x2,y2)]为任意2点(x1,y1)，(x2,y2)处随机场特性值之间的自相关系数；fi(.)和λi分别为自相关函数对应的特征函数和特征值。

采用描述参数空间自相关性的高斯型自相关函数所模拟的参数随机场分布平滑度和连续性较好[8]，故本文选取高斯型自相关函数，表达式为：

(2)

式中：lh和lv分别表示水平和垂直方向上的相关距离，用于表征参数空间变异性的自相关程度，相关距离越大对应的尾矿材料参数的空间自相关性越强。

根据式(2)可计算得到原始空间不同点处的随机场特性值之间的自相关系数。一般水平相关距离是垂直相关距离的10倍左右，水平相关距离在10～40 m范围内，垂直相关距离变化范围为1～3 m[9]。

当采用式(2)高斯型自相关函数时，式(1)没有解析解，为此本文采用wavelet-Galerkin技术[10]进行数值求解。基于自相关函数的特征解可将随机场H(x,y)展开为：

(3)

式中：(x,y)为随机场区域中的任意坐标点，(x,y)∈Ω；ξXi,j为参数随机场离散的独立标准正态随机变量；μlnXi和σlnXi分别为相应参数随机场lnXi的均值和标准差；n为截断项数，与随机场离散的随机变量数目对应。截断项数n取决于精度要求和自相关函数的形式，文献[11]～[12]建议采用随机场期望能比率因子ε≥95%作为确定截断项数n取值的依据。

2 尾矿坝可靠度非侵入式随机分析方法

通过K-L展开方法得到参数随机场特性值后,需要进行含大量随机变量的尾矿坝边坡可靠度分析。尾矿坝渗流分析和边坡稳定一般借助有限元软件实现，因此尾矿坝安全系数与尾矿材料参数之间是非线性隐式函数关系。传统的MCS、一次二阶矩等可靠度方法不能有效求解含大量随机变量的极限状态函数是隐式的尾矿坝可靠度问题。为此，本文将近几年发展起来的非侵入式随机有限元法[8]拓展到尾矿库工程领域，采用Hermite随机多项式展开(Hermite Polynomial Chaos Expansion，PCE)代替尾矿坝边坡安全系数FS与尾矿材料参数ξ之间的非线性隐式函数关系：

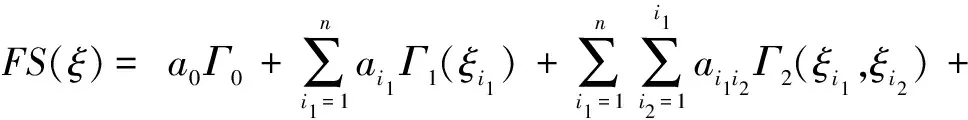
(4)

式中：n为随机变量的数目；ξ=(ξ1,ξ2,…,ξn)T为独立标准随机向量，与式(1)参数随机场离散的随机变量一一对应；Γp(.)表示为p阶Hermite随机多项式展开；a0,ai1,ai1i2,ai1i2i3,…为待定系数，其数目为(n+p)!/(n!p!)。

接着，采用拉丁超立方抽样技术(Latin Hypercube Sampling，LHS)[13]产生输入参数随机样本点，代入有限元程序或岩土商业软件计算安全系数，再根据式(4)建立线性代数方程组求解多项式展开系数。一旦确定了尾矿坝安全系数和输入参数ξ的显式函数关系，即安全系数代理模型，便可建立新的显式函数表达的尾矿坝稳定可靠度分析极限状态函数：

G(ξ)=FS(ξ)-1.0

(5)

基于采用Hermite随机多项式展开建立的代理模型，利用100 000次MCS方法计算尾矿坝失稳破坏概率。显然，该方法不仅实现了可靠度分析和确定性有限元分析的不耦合，而且直接使用代理模型计算安全系数FS，无需进行大量的有限元计算，提高了计算效率。

3 工程应用

以西木尾矿库工程[14]为例，探讨尾矿坝材料渗透系数和内摩擦角空间变异性对尾矿坝稳定可靠度的影响。西木矿区位于加拿大魁北克省鲁恩-诺兰达以东约40 km的鲍斯凯镇，于2004年被发现。西木尾矿坝坝高15 m，大坝在建设结束时的几何形状，初始模型中各层材料分布、层厚和层宽如图1所示。各个土层的物理力学参数见表1。土层下限是基岩和过密的冰碛层，在大坝建设之后保持平衡，被认为是稳定地层。

图1 尾矿坝材料剖面及有限元网格Fig.1 Material profile and finite element mesh of the tailing dam

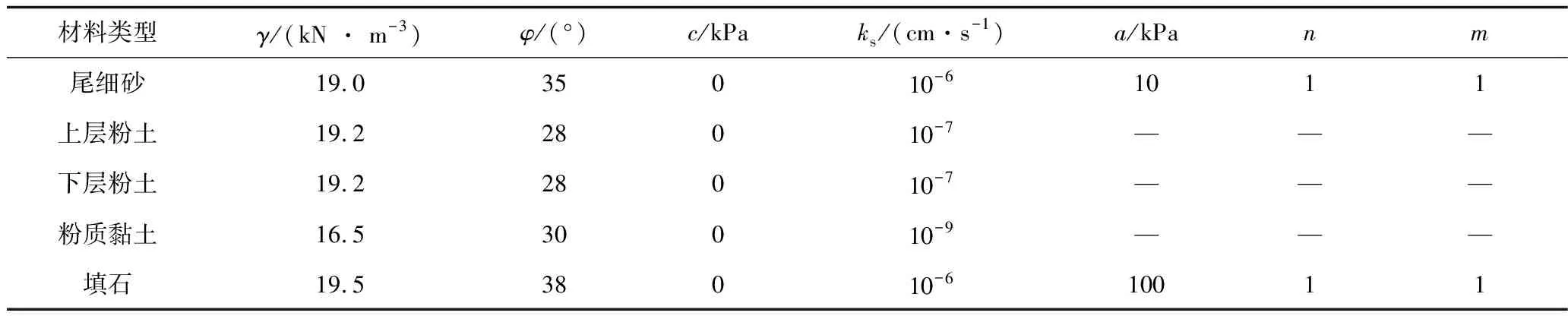
表1 尾矿材料物理力学参数Table 1 Physical and mechanical parameters of tailings materials

注：γ，φ，c和ks分别为尾矿材料的重度、内摩擦角、黏聚力和渗透系数；a,n和m为土水特征曲线拟合参数。

3.1 有限元模型及计算参数

西木尾矿坝有限元模型如图1所示，一共划分为10 685个节点和10 407个网格大小为0.5 m的四边形和三角形混合单元。边界条件为：上游水位(左侧)13 m，下游水位(右侧)8 m，并在下游边坡(右侧)设置了潜在渗流面。基于SEEP/W模块对西木尾矿坝进行饱和渗流分析，再将得到浸润线和孔隙水压分布等渗流结果导入到SLOPE/W模块，采用摩根斯坦-普莱斯法计算的安全系数FS=1.931，最危险滑动面如图2所示。所计算的安全系数和临界滑移面与Coulibaly等[14]计算的安全系数1.967和临界滑移面基本一致，说明了该确定性有限元分析的有效性。

因受基质吸力、含水量、渗透率等因素的影响，因此对西木尾矿坝进行饱和-非饱和渗流分析十分必要。本文将填石和尾细砂视作非饱和材料，采用目前应用广泛的Fredlund-Xing[15]模型表征的土水特征曲线(SWCC)模拟体积含水量与基质吸力之间的函数关系。模型拟合参数a为进气值相关的土性参数；n为与SWCC斜率相关的土性参数；m为与残余含水率相关的土性参数[16]，参数取值见表1。图3(a)和3(b)分别给出了尾细砂土水特征曲线与渗透系数函数。将饱和-非饱和渗流分析结果导入到SLOPE/W模块，采用摩根斯坦-普莱斯法计算得到西木尾矿坝安全系数FS=1.944，大于在所有尾矿材料为饱和状态下计算的安全系数。

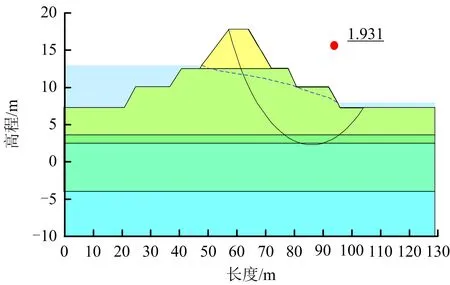
图2 尾矿坝稳定性分析结果Fig.2 Stability analysis results of the tailings dam

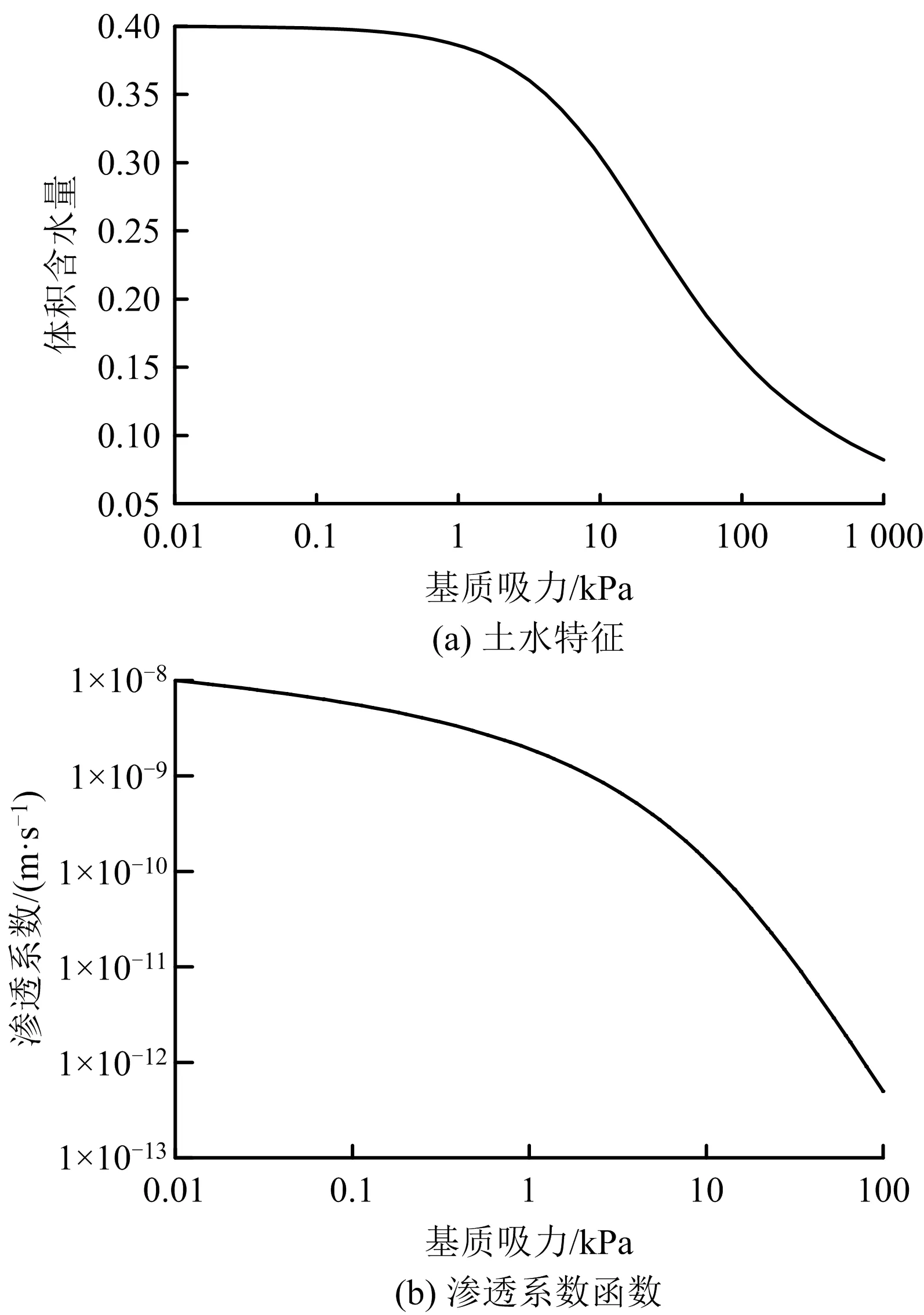
图3 尾细砂土水特征与渗透系数函数曲线Fig.3 Soil-water characteristic curve and permeability coefficient function curve of tailings fine sand

另外，尾矿坝上的局部坍塌和滑移大多是由于地震导致尾部或地基土液化引起的[14]。为此，本文考虑Ⅶ级地震作用，进一步对该尾矿坝进行稳定可靠度分析。根据建设部颁布的《关于统一抗震设计规范地面运动加速度设计取值的通知》规定，Ⅶ级地震设计基本地震加速度取0.1 g，竖向地震影响系数的最大值取水平地震影响系数最大值的65%[17]。采用拟静力法模拟Ⅶ级地震作用，同样通过非饱和渗流稳定分析得到安全系数FS=1.418，图4给出了最危险滑面位置。根据尾矿设施设计规范[18]可知，该尾矿坝在Ⅶ级地震作用下仍处于稳定状态。

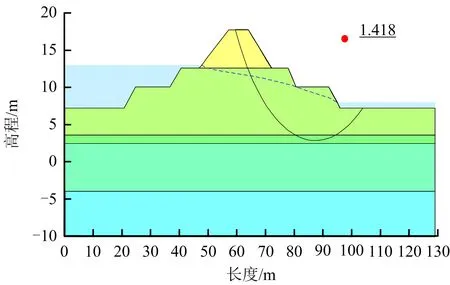
图4 地震作用下尾矿坝稳定性分析结果Fig.4 Stability analysis results of tailings dam under effect of earthquake

3.2 尾矿坝稳定可靠度分析

如前所述，受到尾矿坝长期多循环水力充填以及固结沉降的作用，尾矿材料强度参数存在较大的离散性和空间变异性，与尾矿材料抗剪强度参数空间变异性相比，尾矿材料重度空间变异性较小，一般小于10%，可视作常量。故本例仅考虑尾矿材料渗透系数ks和内摩擦角φ的空间变异性，并假设尾细砂、粉土、粉质黏土和填石的ks，φ均服从对数正态分布，尾矿坝材料参数统计特征见表2。

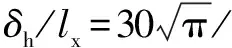
表2 尾矿材料参数统计特征Table 2 Statistical characteristics of tailings materials parameters

图5 尾细砂渗透系数随机场的典型实现Fig.5 Typical realization of random field for permeability coefficient of tailings fine sand

在此基础上，利用LHS法对输入的变量进行抽样，根据参数统计特征生成随机变量和随机场数据，分别赋到尾矿坝模型，然后通过渗流有限元和稳定分析得到FS，再采用Hermite展开多项式建立FS代理模型(即FS与随机变量和随机场离散的随机变量之间的显式函数关系)。图6比较了由不同方法计算的极限状态函数累积分布函数(CDF)曲线。由图6可见，分别进行2 000，4 000和10 000次渗流有限元及稳定性分析构建FS代理模型，对应的二阶PCE+MCS方法计算的极限状态函数的CDF曲线非常吻合，并且与10 000次直接LHS方法的计算结果仅仅在低概率区域存在微小差别。其原因是10 000次直接LHS方法对于低失稳破坏概率(<10-3)水平尾矿坝可靠度问题，计算精度不够。

图6 极限状态函数累积分布曲线的比较Fig.6 Comparison on cumulative distribution curves of limit state functions

由图6极限状态函数的CDF曲线可以直接计算尾矿坝失稳破坏概率。表3比较了不同方法计算的尾矿坝失稳破坏概率。从表3可以看出，西木尾矿坝失稳破坏概率水平很低，二阶PCE+MCS方法(Np=2 000)，二阶PCE+MCS方法(Np=4 000)和二阶PCE+MCS(Np=10 000)方法计算的破坏概率分别为8.6×10-4,8.1×10-4，7.6×10-4，可见3种方法计算的破坏概率非常吻合，和10 000次直接LHS方法计算的9.9×10-4也基本一致，说明了本文非侵入式随机有限元法的有效性。此外，与10 000次直接LHS方法相比，二阶PCE+MCS方法只需要进行2 000次尾矿坝渗流有限元和稳定性分析就可以满足计算精度要求，计算量是直接LHS方法的1/4，可见本文提出的方法具有较高的计算效率，为解决考虑多个尾矿材料参数空间变异性的低概率水平尾矿坝稳定可靠度问题提供了一条有效路径。