基于PCA-MDBN模型的开都河年径流预测

(新疆塔里木河流域管理局，新疆 库尔勒 841000)

河川径流预测对于水库合理调度、农业防汛抗旱、区域水资源合理开发与优化利用、区域社会经济规划的制定具有重要意义。目前，国内外学者常采用投影寻踪回归[1]、灰色理论[2]、神经网络[3]、支持向量机、最小二乘支持向量机[4-5]等单项预测方法对降水、废水治理、地下水等领域的参数进行预测。由于河川径流变化影响因子众多，且各因子之间相互关联并呈现非线性变化，采用数学方法及传统神经网络很难精准预测，且在进行数据训练时存在局部收敛和计算效率差的问题。

近年来，随着数据量的增加及计算机性能的提高，基于深度信念网络(deep belief network，DBN)通过构建非线性深层次的网络结构，可提取数据高层特征并能准确拟合复杂函数，并且具有较强的数据预测能力和数据分类及识别能力。本文在前人研究的基础上，基于粒子群算法(particle swarm optimization，PSO)优化的多变量深度信念网络(multi-variable deep belief network，MDBN)构建河川径流预测模型，为其高精度预测奠定了良好基础。

1 模型计算方法

1.1 深度信念网络

1.1.1 深度信念网络结构

深度信念网络(deep belief network，DBN)是深度研究中应用较为广泛的一种网络结构，于2006年由Geoffery Hinton首次提出[6]。随着数据量的增加和计算机性能的提高，DBN方法被广泛应用于人工智能领域。一个典型的DBN结构相当于一个高度复杂的有向无环图，可分解为多个受限玻尔兹曼机(restricted boltzmann machine，RBM)。RBM作为DBN的基本组成单元，主要由两层神经元组成(其网络结构见图1)。其中，用于训练数据输入的可视层和特征提取的隐含层单元彼此之间互相连接，但同层内的神经元节点无连接，并且同层节点之间条件独立，连接权重用矩阵W表示。当隐含层结点数量达到一定值时，可用此网络模型表示任意离散分布。

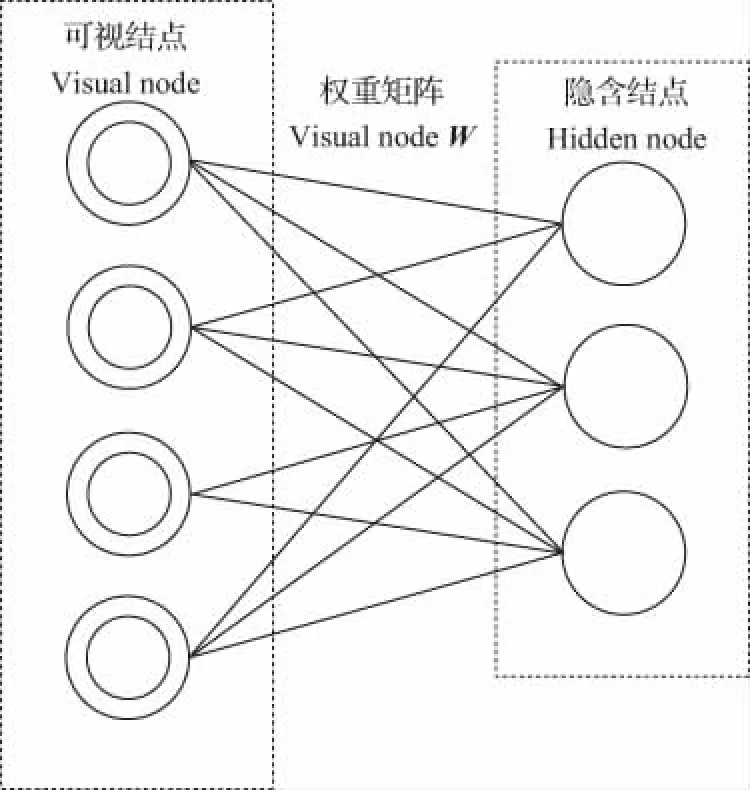
图1 RBM模型基本结构

1.1.2 深度信念网络训练与生成

DBN作为一种深度网络结构，训练过程主要包括无监督的预训练和有监督的反向传播网络的微调两个步骤。在无监督预训练阶段，分别单独训练每层RBM网络，为提取重要特征信息，以重构误差函数为目标函数，使单元特征向量映射于不同特征空间，进而得到预训练网络初始权重。然后，在微调阶段，利用反向传播对整个网络进行优化。

1.2 粒子群算法

粒子群算法(particle swarm optimization，PSO)的基本思想源于对鸟类群体觅食行为研究，而提出的一种全局随机搜索算法，目前，已经广泛应用在约束优化和多目标优化等领域。在经典PSO算法中，每个优化问题的解被类比为搜索空间中的一只鸟，将其称之为“粒子”。每个粒子代表解空间中的一个候选解，有一个初始化速度和位置，由适应度函数计算粒子适应值。每个粒子的速度决定它们在解空间中搜索的方向和位置，且每个粒子都具有记忆功能，能够记住搜索到的最佳位置。算法在每次迭代过程中，粒子会根据两个极值：粒子本身当前找到的最优解和目前整个粒子群找到的全局最优解，来更新自己的速度和位置进行搜索，直至找到最优解。

PSO优化算法通过迭代搜索每个粒子的当前最优解，并利用适应度值评价解的优劣程度，从而确定全局最优解。作为一种随机搜索、并行优化的算法，PSO算法具有简单易行、鲁棒性好、收敛速度快等优点，能以较大概率找到全局最优解。

2 河川径流预测模型构建

预测模型构建步骤如下：

a.收集与年径流变化相关的气象信息，包括年降水量、年蒸发量、年均气温、年日照时数与年均风速等原始数据集，并对数据进行归一化处理。

b.利用PCA(principal component analysis)方法分析年径流量与气象变量之间的相互作用关系，根据各个变量的贡献率筛选年径流量预测的主影响因子。

c.利用小波阈值降噪方法通过正交试验确定各个变量的最佳小波降噪方案，对选取的主因子变量进行降噪，得到最终的辅助变量数据样本，并划分为训练样本集及测试样本集。

d.构建MDBN模型，采用试验方法对MDBN模型进行初始化设置，选择最优设置结果，包括隐含层节点以及隐含层层数等。

e.利用PSO优化算法对构建好的MDBN网络参数设定进行优化，得到最优迭代次数和学习率组合。

f.将最优网络参数设置组合带入MDBN预测模型，得到最终的年径流量预测模型，将测试样本输入优化后的预测模型，计算径流量预测结果。

2.1 关键影响因子筛选

评价一个变量因子是否为关键影响因子的标准是其提供信息的能力，PCA方法可以确定每个变量的贡献率，进而对各个变量的作用关系进行评价，在保留原始数据主要特征前提下，对问题进行定量分析，减少输入数据维度。因此，本文采用PCA方法计算相关系数矩阵，分析数据间的线性关系从而对数据进行筛选和压缩，实现关键变量因子的选取。

2.2 数据降噪处理

由于径流影响因素复杂，获取的数据存在大量噪声。消除数据噪声是模型构建的重要基础。传统降噪方法，例如傅里叶变换等，只能描述信号在频率域中的变化，无法分辨出信号在时间轴上的瞬时变化。而小波降噪法对信号具有自适应性，可以在去除噪声的同时保留原始信号信息，具有优越的局部化性能。

小波降噪法大致分为3类：小波阈值降噪方法、模极大值重构法、空域相关滤波法，其中小波阈值降噪方法实现简单、计算量小、降噪效果良好，因此本文采用小波阈值降噪方法，实现模型输入关键影响因子噪声的去除，为预测模型构建提供良好的数据基础。

2.3 MDBN模型构建

本文采用MDBN模型预测年径流量，经过主成分分析筛选所得关键影响因子作为训练样本送入MDBN的可视层。当对径流量进行预测时，MDBN网络结构的隐藏层从高维复杂输入数据提取相关特征，逐层激活强相关影响因子，将无关冗余信息弱化并抑制，使用非监督贪婪逐层方法预训练模型获得初始权重，最后采用对比散度(contrastive divergence，CD)算法逐层训练各个RBM。

3 研究区概况

开都河发源于新疆天山山脉中部的依连哈比尔尕山南坡，河源高山区终年积雪，有现代冰川840条。开都河流经和静县、焉耆回族自治县和博湖县后注入全国最大的内陆淡水湖——博斯腾湖，河流全长560km，多年平均径流量为35.18亿m3。

开都河流域深居欧亚大陆腹地，远离海洋，呈现明显的干旱大陆性气候特征，流域多年平均降水量为47.3～75.0mm，集中于6—8月，多年平均蒸发量(20cm蒸发皿)1887～2777mm，夏季炎热，冬季寒冷少雪，多年平均气温8.2℃，日照时数3105h。

本文以新疆开都河大山口水文站1956—2015年60年的实测资料为例，利用前述方法对河川年径流量进行预测研究。

4 结果与分析

4.1 数据预处理

本文使用收集到的开都河大山口水文站1956—2015年60年径流数据及相关气象数据(包括年降水量、年蒸发量、年均气温、年日照时数与年均风速5个因素)，首先对其进行标准化和归一化预处理，并利用PCA方法对5个气象变量进行相关性分析，计算得到特征值与累计贡献率(见表1)。

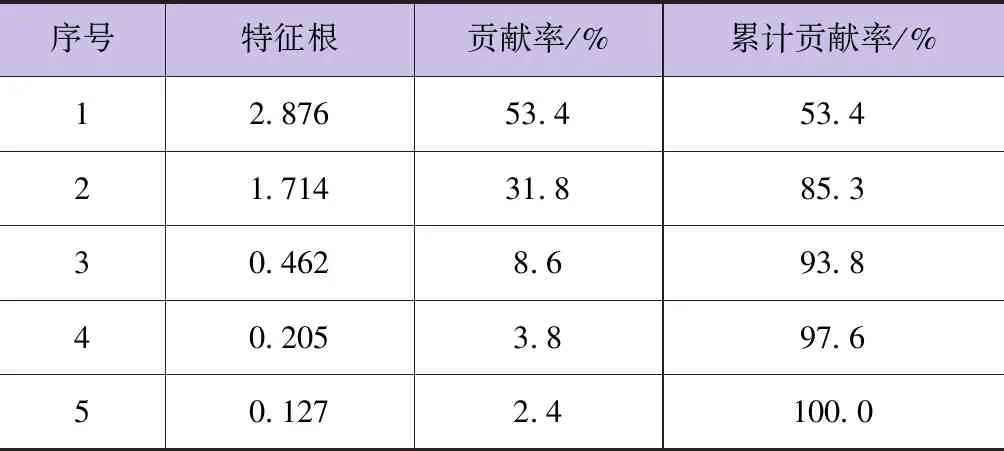
表1 年径流量相关气象变量特征值与累计贡献率

由表1可知，前3个主成分的累积贡献率达到93.8%(其对应的载荷矩阵见表2)。从载荷矩阵可以得出，年降水量对第1主成分贡献大，年蒸发量对第2主成分贡献大，年均气温对第3主成分贡献大，年均风速对第4主成分贡献大，年日照时数对第5主成分贡献大。因此，最终选择年降水量、年蒸发量、年均气温3个因子为年径流量主要影响因子。

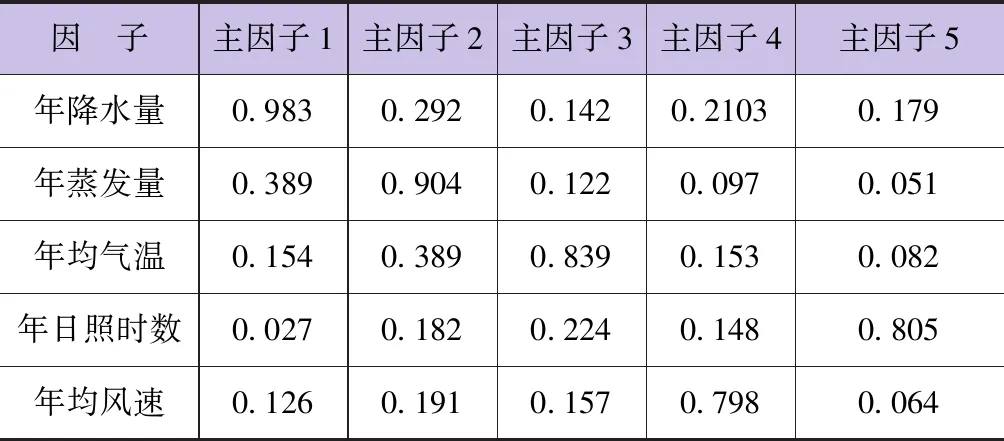
表2 年径流量相关气象变量载荷矩阵

完成关键影响因子筛选后，利用小波阈值降噪方法对经过标准化和归一化处理后的3个气象变量以及年径流量数据进行降噪处理。由于小波基、阈值选取方法以及阈值量化函数的选取都对小波阈值降噪效果有明显影响，但迄今没有具体的最优参数选择方法。因此，本文采用正交试验方法，选取最优小波降噪方案对数据进行降噪(结果见表3)。

将1956—2015年的开都河径流及气象数据分为训练集和测试集，其中1956—2005年数据用于训练(共计50组)，2006—2015年数据用于模型性能测试(共计10组)。

表3 各变量最优小波降噪方案及结果

由于MDBN网络参数(隐含层节点数及隐含层层数)直接影响算法性能，当隐含层层数设置为4、8、12，隐含层节点个数设为100、250、500、1000时，均方根误差RMSE达到极小值。然后，通过多次训练效果验证，得到训练及微调时的最佳网络参数：学习率为0.1，迭代次数为100。为了探索网络结构参数对模型学习性能的影响，对隐含层层数与隐含层节点数进行两两组合，选取RMSE值最小的MDBN网络结构设置。由表4可知，当隐含层层数为12，隐含层节点数为500时，网络在测试集上的RMSE误差达到最小，其值为0.01526。因此，得到MDBN最佳的网络参数设置：输入层节点数为3，输出层的神经元数为1(年径流量)，隐含层数为12，隐含层节点数为500，初始化学习率为0.1，初始化迭代次数为100。

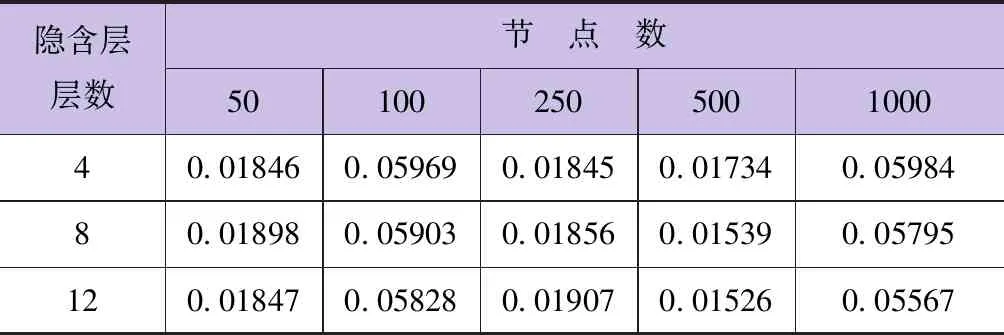
表4 MDBN不同网络参数下的RMSE值

为有效减少计算复杂性和提高预测性能，利用PSO优化算法简单易行、收敛速度快、设置参数少的优点，将粒子群在MDBN的解空间追随最优粒子进行全局搜索，进而实现对MDBN网络的优化；并设定 PSO优化算法初始种群规模为30，进化代数为20，最小训练停止误差为10-4，加速因子c1和c2均设置为1.5，学习率粒子的取值区间为[0，1]，迭代次数粒子的取值区间为[10，2000]。

4.2 结果分析

本文将PSO-MDBN与BP神经网络(back propagation neural network, BPNN)预测方法进行了对比，误差评价体系采用均方根误差(root mean square error，RMSE)、平均相对百分比误差(mean absolute percentage error，MAPE)与平均绝对误差(mean absolute error，MAE)。

将训练样本集输入已构建的PSO-MDBN网络进行训练，然后将测试样本在已预训练的网络中进行比较分析，并与BPNN、DBN方法进行对比(PSO-MDBN、传统DBN、BPNN方法在预测样本的具体误差值见表5)。

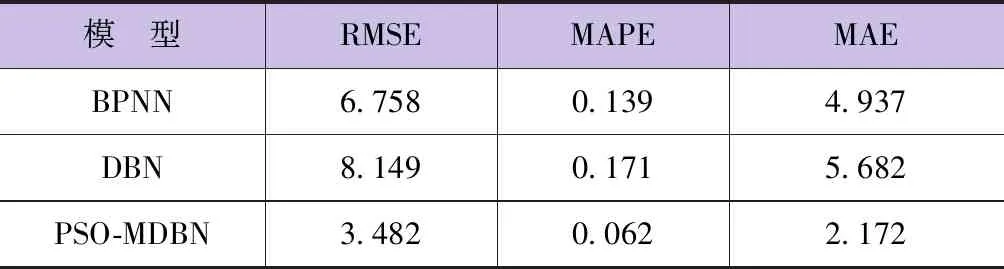
表5 不同模型对年径流量的预测性能对比

从表5可知，BPNN对年径流量预测的MAPE值为13.9%，未经PSO算法优化的MDBN模型的 MAPE值为17.1%。然而，本文提出模型的MAPE值为6.2%，与2种传统方法相比，其MAPE值分别降低了7.7%、10.9%。同时，PSO-MDBN方法的RMSE和MAE值也明显小于其他2种方法的误差值。

计算结果表明，本文的构建模型预测精度明显优于其他2种传统方法，经过粒子群算法优化的MDBN模型，其不仅提高了网络收敛速度，同时也提高了模型预测精度。

5 结 论

针对因河川径流复杂多变，导致传统方法难以准确预测的问题，为提高预测精度，本文提出了一种基于PSO-MDBN的预测模型。为避免变量冗余导致计算效率下降的问题，利用 PCA和小波降噪方法进行数据相关性分析并选取关键因子参数作为模型输入。基于DBN网络构建多变量预测模型，并利用PSO算法寻找最优网络参数，进而提高模型预测精度及计算效率。研究结果表明，该模型实现了平均百分比误差为6.2%的预测精度，与传统BPNN、DBN方法进行比较，其MAPE值分别降低了7.7%、10.9%。良好的预测效果充分证明了基于PSO-MDBN的径流预测模型的有效性和实用性，及解决复杂、非线性问题的预测能力。