基于非线性规划的渣土边坡坡形优化
2020-01-09曾江波姚文敏肖林超
曾江波,杨 龙,姚文敏,肖林超 ,鲁 健
(1.深圳市勘察测绘院(集团)有限公司,广东 深圳 518028;2.中国地质大学(武汉)工程学院,湖北 武汉 430074)
0 引言
随着我国经济的快速发展,城市建设过程中产生的渣土日益增多,据资料统计和推算,我国建筑施工产生的渣土年均超过亿吨,且有快速上升的趋势,其中约79.3%经受纳场填埋处理[1]。如何在有限的受纳场内处理尽可能多的渣土,是渣土边坡设计时所面临的问题。与此同时,经填筑形成的渣土边坡,在外部因素的作用下,易引发边坡失稳[2-3]。因此,在当前城市化快速推进的背景下,会面临更多渣土边坡问题,其稳定性研究与优化设计已成为岩土工程中关注的热点。
渣土边坡由于物源广泛,坡体物质组分复杂,物理力学参数具有较大空间变异性,使得稳定性评价结果不可靠[4]。渣土边坡设计与评价不合理,可能引发滑坡地质灾害。例如,2015年12月,深圳市光明新区红坳渣土场边坡滑坡,因超高填筑以及未有效排水致使土体软化,导致77人死亡[5-7]。关于坡形优化设计,国内学者对矿山、路堑等人工边坡的坡形优化开展了一些研究,如祝玉学等[8]考虑采矿效益利用系统分析与仿真技术提出露天矿边坡优化设计方法。邱恩喜等[9]以红层软岩边坡为对象,提出基于岩体质量评价的坡度优化计算公式。边世斌等[10]基于期望造价提出黄土路堑边坡优化设计的方法。叶万军等[11]基于坡面稳定性,建立了黄土高边坡优化模型。渣土边坡优化设计与上述边坡有所不同。在坡形设计上,堆填的过程人为可控,设计方案对边坡的长期稳定性起着关键作用;在物质组成上,渣土的来源较广泛,坡体物质组成较为复杂,物理力学性质差异大;在优化目标上,由于受纳场处理渣土,缓解了城市处理建筑垃圾的压力,产生一定的经济效益。最优的设计方案,在满足足够稳定性前提下,堆填尽可能多的渣土,从而获得最大的效益,而目前相关理论的深入研究工作较少。
本文基于非线性规划的理论方法,提出了既能考虑渣土边坡填筑的经济性与稳定性,又能结合渣土自身强度特性的渣土边坡坡形优化设计方法。首先以简化的二级渣土边坡为例进行了坡形优化,然后将该方法运用于实际的渣土边坡工程案例中,最后讨论分析了三级边坡的优化设计,说明该理论方法也同样适用于多级渣土边坡的坡形优化,可为实际渣土边坡施工设计提供具有针对性的指导意见。
1 渣土边坡优化设计方法
1.1 渣土边坡模型建立
根据当前广东省出台的余泥渣土受纳场施工技术规范,渣土边坡施工通常采用分层碾压,逐级堆填,设计成多级台阶状的边坡,其坡角、台阶高度、台阶宽度等需按照规范进行设计施工[12](图1),渣土受纳场通常利用山体天然的围堰作用,选择三面环山的洼地作为填筑库区。根据渣土边坡的几何形态特征,将堆填要素划分为:边坡的坡角θ,台阶宽度d,台阶高度h,台阶数n,堆填区坡底允许的填筑范围L。
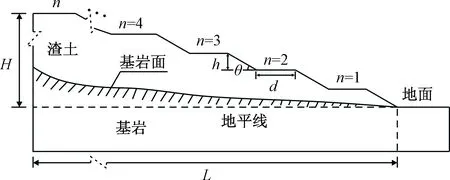
图1 多级渣土边坡示意图Fig.1 Multi-stage slope sketch of construction solid waste
1.2 优化设计模型
通常优化设计包括三个基本要素:决策变量(优化变量)、约束条件和目标函数[13],因此,开展渣土边坡的优化设计,需要明确优化目标,优化变量与约束因素。渣土受纳场通过收纳渣土获取一定的经济效益,且随着填筑渣土量增大而增大,因此,渣土填筑量可作为边坡优化设计的目标函数,坡形参数作为优化变量。根据如图1所示的多级渣土边坡模型,假定各级台阶设计的高度、宽度、坡角均相等,则根据坡形要素确定渣土的堆填面积S,表达式为:

(1)
式中:S——填筑面积/m3;
h——台阶高度/m;
d——台阶宽度/m;
L——堆填区长度/m;
θ——坡角;
n——台阶数;
C——基岩出露面与地表水平线所围面积/m2。
受纳场填筑形成的边坡要求保持足够的稳定性,而边坡稳定性的影响因素众多,不仅与边坡的几何坡形因素相关,也与渣土自身物理力学强度特性有关,需要明确关键影响因素,结合渣土的强度特性开展具有针对性的优化。笔者采用正交设计,确定影响边坡稳定性的关键因素,并建立与稳定性系数之间的定量关系,同时考虑渣土边坡施工技术规范对边坡稳定性的要求,得到安全约束条件,此外,边坡的几何边界作为几何约束条件。因此,本文根据确定的主要因素,建立相应的组合关系,来满足优化目标,利用三者来构建边坡优化设计模型,其表示形式如下:
maxS(x)

(2)
式中:S(x)——填筑面积;
Gn(x)——几何约束;
Fm(x)——安全约束;
N与M——相应的约束条件个数。
渣土填筑面积与坡形参数存在非线性的定量关系,因此,渣土边坡优化模型转化为一个寻求最优坡形参数设计值的非线性规划问题。
2 渣土边坡坡形优化
渣土边坡台阶数n与受纳场填筑的范围L有关,当填筑范围L较大,则可采用逐级放坡的方法进行填筑,形成多台阶边坡。由图1知,不规则起伏的基岩地面与水平线所围面积为C,当在某特定地形的受纳场填筑时,C为确定的常量,如果基岩地面起伏较缓,则C对目标函数S的最大值求解没有影响,因此,可合理地简化目标函数,假定地面水平,此时C为零。简化的二级渣土边坡模型如图2所示,其中堆填范围L长度为120 m,以下开展对此边坡模型的优化设计。

图2 二级渣土边坡模型Fig.2 Model of two-storied slope of construction solid waste其中:L—坡底范围长度;d—台阶宽度;θ—坡角;h—台阶高度。
2.1 正交试验方案设计
基于正交试验,可分析出边坡稳定性的控制因素,笔者考虑了渣土的容重(R1)、黏聚力(R2)、内摩擦角(R3)、台阶高度(R4)、台阶宽度(R5)、坡角(R6)等六个因素。为了保证试验结果可靠性,每个因素选择五个水平(表1)。其中渣土的容重14~22 kN·m-3,黏聚力8~32 kPa,内摩擦角10°~30°;坡形参数参考规范取值[12],台阶高度5~13 m,台阶宽度4~8 m,坡角15°~35°,将稳定性系数作为结果的评价指标。不考虑因素之间的交互作用,根据影响因素和水平,选择L25(56)规范化的正交表格,正交试验的因素水平如表1所示。
设计方案按照L25(56)正交表,各因素不同水平进行组合(表2),共计25组试验。稳定性的计算采用加拿大岩土专业软件GEO-STUDIO中SLOPE/W模块内置的刚体极限平衡Morgenstern-Price原理来计算边坡的稳定性系数,计算结果见表2最后一列。
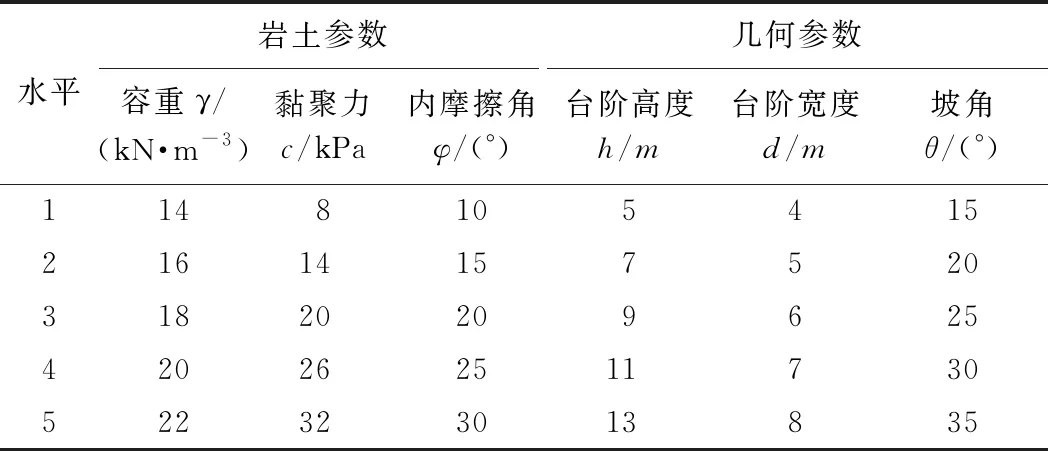
表1 因素水平表
2.2 结果分析
边坡稳定性系数的波动水平可用于分析各因素对其影响的规律。正交设计中极差分析用于评价边坡稳定性的敏感因素,结果如表3所示。根据表3最后一行,对各因素下的极差大小进行排序,即R3>R6>R4>R2>R5>R1,可得到边坡稳定性敏感因素的主次顺次,依此为内摩擦角、坡角、台阶高度、黏聚力、台阶宽度、容重。分析结果可以看出,渣土的强度指标内摩擦角φ和黏聚力c以及坡形指标中的坡角θ与台阶高度h对边坡稳定性较大,而台阶宽度d与容重γ的影响并不显著。
为了更加直观分析各因素对稳定性的影响规律,做出各因素对稳定性系数影响的趋势分布图(图3)。当稳定性对某一因素较为敏感时,即在此因素的不同水平下,稳定性系数波动幅度较大。依此原则,从图3可以看出,内摩擦角对稳定性的影响最大,边坡坡角与台阶高度对稳定性也有着显著影响,由此说明,坡角与台阶高度过大均不利于边坡稳定,而渣土的容重与台阶宽度对边坡稳定性影响并不显著。综合以上分析,渣土边坡稳定性的关键影响因素为内摩擦角、黏聚力、坡角和台阶高度。
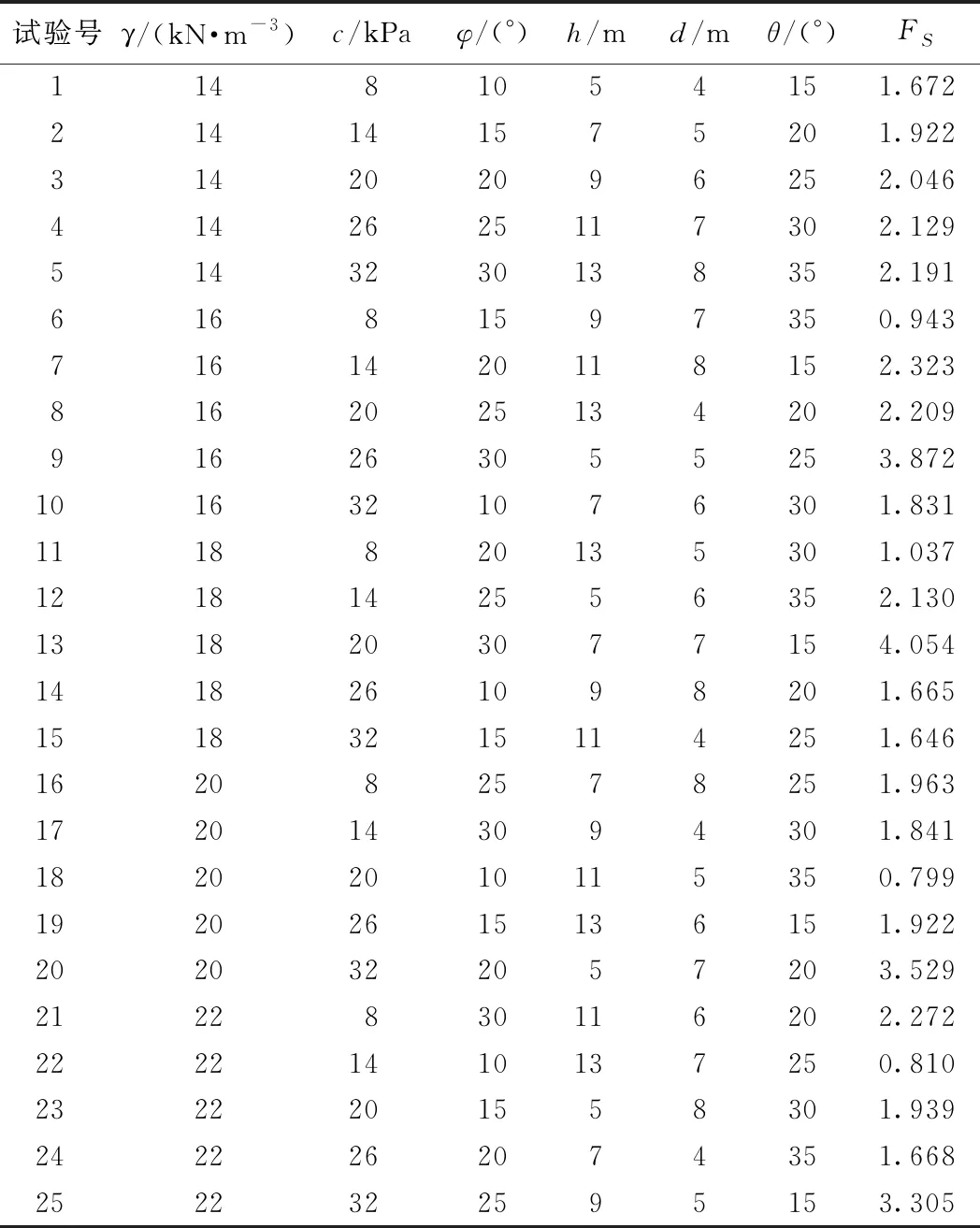
表2 正交设计试验与计算结果
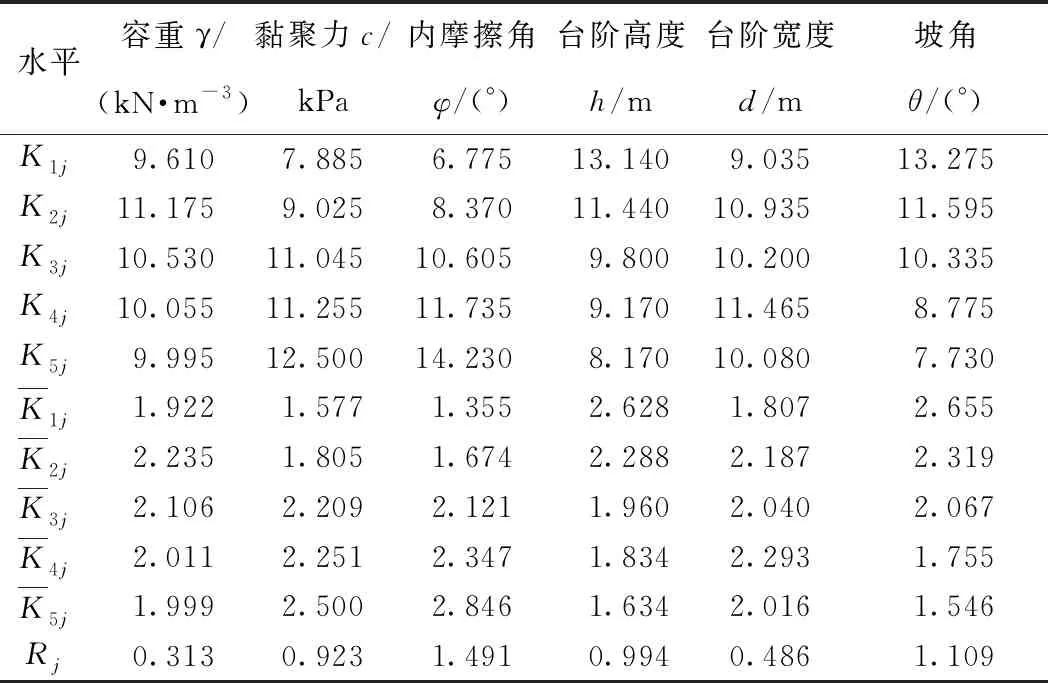
表3 各因素的极差分析
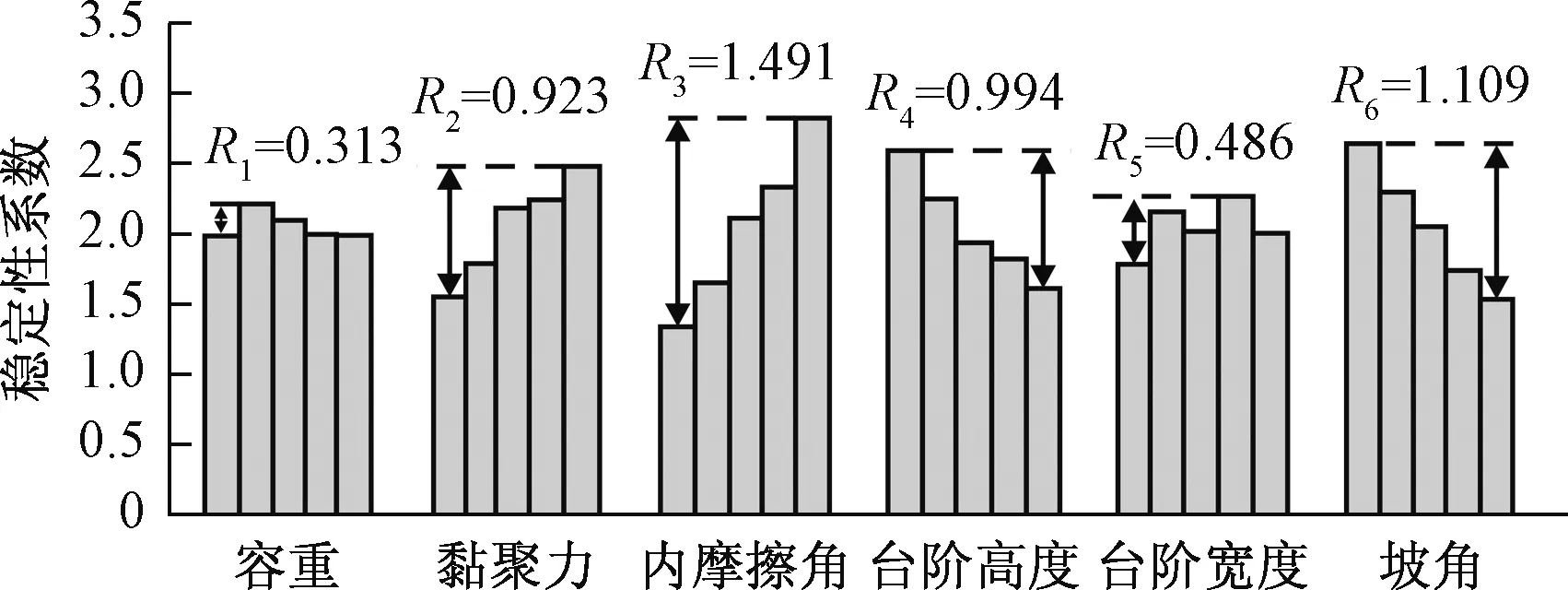
图3 各因素不同水平下的稳定性系数趋势图Fig.3 Trend chart of safety factor under different levels of the factors
2.3 坡形优化设计
上述分析表明,渣土边坡稳定性与渣土自身物理力学性质有关,开展坡形优化,可结合渣土力学特性,并要考虑渣土的经济性,即分析渣土受纳场的最大堆填库容量问题。渣土填筑方量与边坡的坡面形态(坡角、台阶高度、台阶宽度等)密切相关。因此,本文基于非线性规划理论,建立了以填筑方量为目标函数,以边坡稳定性与几何边界为约束条件下的渣土边坡优化设计模型。
2.3.1目标函数
受纳场渣土的填筑量可作为该受纳场产生经济效益的有效评价指标。如图2所示的二级边坡模型,厚度取1 m,则渣土填筑量可用面积S表示。由公式(1)可推导出此边坡面积S的表达式:

(3)
式中:S——填筑面积;
h——台阶宽度;
θ——填筑坡角;
L——坡底长度;
d——台阶宽度。
由公式(3)看出,求解目标函数的最优值,即为分析一个非线性规划问题。本文主要依据边坡的稳定性满足设计要求与几何边界有界性,分别建立安全约束条件与几何约束条件。
2.3.2约束条件
2.3.2.1安全约束条件
安全约束条件主要考虑设计边坡的稳定性满足相关规范要求。前面分析表明,土的内摩擦角、黏聚力、坡角、坡高是控制边坡稳定的关键因素,而其它因素的影响作用不显著,因此,可以将以上四个因素作为优化变量。采用多元回归分析进一步确定稳定性系数与上述四者之间的定量关系。考虑各因素之间无交互作用,回归模型设为:
yFOS=a+b1c+b2tanφ+b3h+b4tanθ
(4)
式中:yFOS——稳定性系数;
c,φ,h,θ——黏聚力、内摩擦角、台阶高度、坡角;
a,b1,b2,b3,b4——多元回归方程的偏回归系数。
采用最小二乘法,利用公式(4)对正交设计的25组实验数据进行多元回归分析,得到方程(5):
yFOS=2.271+0.038c+3.653tanφ-0.122h-
2.567tanθ
(5)
回归模型应用之前需进行显著性检验以及拟合优度标准的评价,其中显著性检验包括对回归方程与回归系数的检验[14]。回归方程采用F统计量进行显著性检验,查F分布表得临界值F0.01(4,25)=4.18[15],计算得F=65.269,则有F>F0.01(4,20),说明稳定性系数与上述四个因素线性关系十分显著。回归系数的显著性检验需要对每个偏回归系数进行检,采用t检验,给定显著水平α=0.01,则以t0.005(20)为标准进行比较,查表知t0.005(20)=2.845 3,而四个因素的|ti(20)|值分别为6.519、10.402、6.950、7.880,均大于临界值t0.005(20),说明此四个因素对边坡稳定性影响十分显著,和此前结论一致。在多元回归分析中,复相关系数R作为拟合程度的评价指标,经计算R2=0.929,说明拟合的效果较好,回归结果较为显著。
从拟合结果看出,在工程参数取值范围内,稳定性系数与上述四个因素存在近线性的定量关系。此处考虑渣土的经济性与对城市居民与经济体的潜在威胁,且未考虑降雨、地震等外部诱发因素,安全系数取1.4。从回归方程(5)也可以看出,前二者为岩土自身的物理力学指标,后两者为边坡的坡形指标,因此,可针对不同强度特性的渣土坡形进行优化设计。本文主要考虑了黏土、粉土、砂土等三种强度特性的渣土,参数取值参考了《工程地质手册》[16],并将参数取值与安全系数带入回归方程(5)式,则可得到相应的安全约束条件(表4)。

表4 不同类型土的强度参数与约束方程
2.3.2.2几何约束条件
几何约束主要考虑边坡几何边界有界与计算结果不受边界影响等条件。对于底部边界,边坡底面与基岩接触,其长度L取场地允许填筑范围的最大值,此处L=120 m;对于左侧边界,边坡的左侧与基岩接触,高度2h作为优化变量;对于右侧边界,此边界为自由边界,并且取决于坡形的设计参数,即台阶宽度d,台阶高度h,以及坡角θ,并且后二者作为优化变量。其中本文θ范围取5°~45°,h范围取3~20 m,台阶宽度由于对边坡稳定性影响不显著,大小取10 m;对于上部边界,此边界为自由边界,同样取决于边坡设计的坡形参数;但同时需要满足:利用刚体极限平衡法搜索的滑面不受上部边界的影响[17],要求坡顶与左侧边界的距离不得低于2.5倍的坡高,才能保证计算结果较为精确。综合上述几何边界的约束条件,可得到以下约束方程:
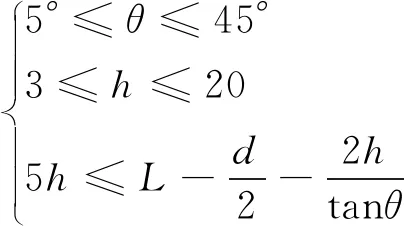
(6)
2.3.3结果计算与分析
满足安全与几何约束条件,则可以求解该边坡优化设计的非线性规划模型最优解。依据前面安全与几何约束条件以及目标函数堆填面积(3)式,利用MATLAB编写的程序进行非线性优化求解。计算表明,存在全局最优解,参数取整后的优化结果见表5。同时对比建筑渣土规范的坡形参数取值[12],本文砂土规范取值是在规范建议的范围内取其上限值,黏土取其下限值,粉土则介于二者之间。优化结果表明,对于黏性土得到最优坡角为20°,最优台阶高度为10 m,最大填筑面积为1 751 m2;对于砂土得到最优坡角为31°,最优台阶高度为13 m,最大填筑面积为2 427 m2;对于粉土,最优值介于二者之间。计算结果表明本文提出的优化设计方法在满足安全性的要求下,填筑方量可以提高30%以上,而目前建筑渣土规范设计是偏安全的,因此对于实际渣土填筑工程,可根据所填筑渣土的力学强度特点,设计更加合理的坡形参数值。

表5 优化结果
如图4所示,作出目标函数与约束条件的图像,更加直观地反映该非线性规划模型,从图4中可以看出,存在全局最优解。根据渣土类型,可以划分为三个安全约束区间,黏性土、粉土、砂土的约束区间依次扩大,堆填面积也随着坡高与坡角的增大而增大,但限制在安全约束条件内,交点处为最优值,对于其它强度特性渣土边坡,如淤泥质土、碎石土等同样可求解对应的最优坡形参数。因此,渣土强度特性制约着边坡坡形设计,考虑对不同强度的类型渣土进行坡形优化是必要的。

图4 基于目标函数与约束条件最优值点确定Fig.4 The optimal points based on the objection function and constraints
3 工程案例分析
3.1 工程概况
深圳某渣土受纳场的原始地貌为丘陵和冲沟,但由于场地大规模渣土堆填,地形发生较大改变,场地中间较为平缓,呈自西南向东北倾伏,在东侧、西侧及北侧边缘顺接原来冲沟的位置形成了边坡,剖面示意图见图5,为二级边坡,经工程地质测绘,边坡角度为21°,总体坡高约为19 m,台阶宽度为8.5 m,坡顶宽度为58 m。根据区域地质资料,未见活动性断层穿越,场地总体上较为稳定。结合现场的钻探资料,自上而下的地层分别为:①人工填土,以黏粒和砂土为主,夹杂少量的碎石、砖头等建筑垃圾,渣土压实不充分,尚未完全固结。②强风化的中粒花岗岩,矿物颗粒为除石英外,其它矿物风化成砂土状,质量等级为V级。③中风化的中粒花岗岩,岩芯呈块状,有裂隙发育,质量等级为IV级。根据现场勘察与室内实验,统计得到岩土的力学参数(表6)。

图5 渣土边坡示意图Fig.5 The ketch of construction solid waste slope
3.2 坡形优化
根据此渣土边坡示意图,不规则多边形ABCD-EA为渣土的填筑部分,边坡模型可简化为规则边坡ABCDEFA,填筑面积为多边形ABCDEFA减去曲边三角形AEF,曲边三角形AEF可通过量测得到面积C,此常数项对非线性规划最优值求解无影响,因此,可利用前面二级边坡优化方法对该实际边坡进行坡形的优化设计,由于平台宽度对坡体稳定性影响不显著,取实际设计值8.5 m,安全系数取1.4,根据坡形参数可以确定目标函数与几何约束,根据坡体物理参数取值可以确定安全约束。其中坡角θ取5°~45°,坡高不大于后缘出露基岩高度21.6 m,允许的堆填范围L为116.5 m,安全系数不低于1.4。因此,可建立如下渣土边坡优化设计模型。

表6 岩土力学参数

(7)
利用MATLAB编写的程序求解该非线性规划最优值,坡形参数的优化结果见表7,结果也表明实际的坡形参数设计值偏向于保守,通过采用优化设计方法,设计参数可适当增大,优化后的坡形如图5所示,此时堆填区域为AB’C’D’E’A,堆填面积可提高9%左右,能进一步发挥受纳场的填筑量。

表7 优化结果
4 讨论
采用该理论方法对二级渣土边坡坡形进行了优化设计,得到了最优的坡形参数,为了验证本文提出非线性渣土边坡优化设计方法对多级台阶渣土的适用性与准确性,对三级边坡也进行了优化设计。如图6所示,为简化的渣土边坡模型。边坡模型堆填范围纵长L为180 m,相应台阶数n取3,同样地面假定为平直基岩面。同样采用L25(56) 正交表进行正交设计,岩土强度参数与坡形取值同二级边坡。
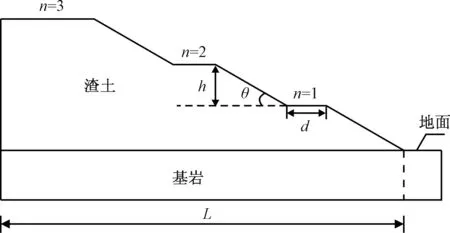
图6 三级渣土边坡模型Fig.6 Model of three-storied slope of construction solid waste
三级边坡正交设计的结果表明,边坡稳定性的敏感因素为渣土的内摩擦角、黏聚力、台阶高度、坡角等四个因素,且与四者之间存在近线性的关系,拟合优度R2为0.918,与二级边坡的结论基本一致,坡形的优化结果见表8,证明该方法可拓展应用到多级渣土边坡的坡形优化中。
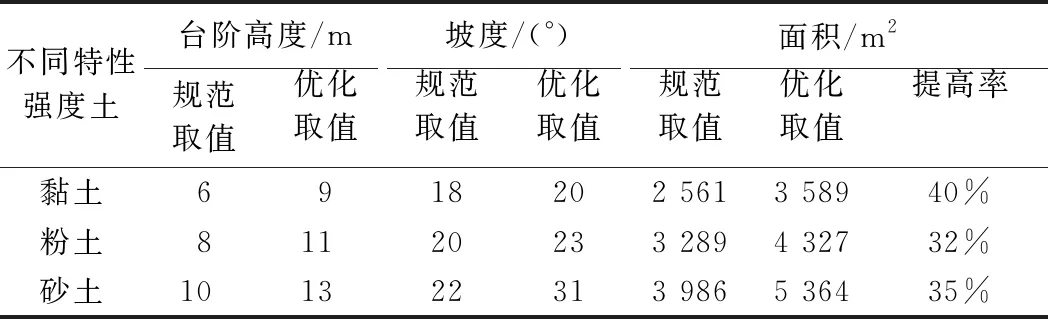
表8 优化结果
采用本文的优化设计方法所得到的最优坡形参数,说明目前的规范坡形参数取值偏向于安全,相对于规范设计值,最大填筑量提高了30%以上,因此对于实际的渣土工程设计施工,可根据渣土自身力学强度特性,选择更加合理的坡形参数,可实现经济效益的最大化。同时对比二级边坡优化设计的结果,三级边坡优化得到的坡形参数略有降低,说明随着边坡填筑的总高度增大,最优坡形参数也会随之降低。
5 结论与讨论
(1)正交设计结果表明,在渣土边坡的稳定性影响因素中,渣土的内摩擦角、坡角、台阶高度、黏聚力等四个因素是控制边坡稳定性的关键因素,并通过多元回归分析,确定了与稳定性系数之间的定量关系,而台阶宽度与容重影响不显著。
(2)建立了渣土边坡的优化设计模型,通过对渣土边坡模型的分析,确定了不同强度特性渣土边坡的最优台阶高度与坡角,并将该方法运用于实际的工程案例中,相比于实际设计值填筑量提高了约9%,因此,在渣土边坡坡形设计中,可根据渣土强度特点,选择合理的坡形参数可进一步发挥受纳场的填筑容量,实现经济效益最大化。
(3)基于两个二级与三级边坡优化的结果,表明本文提出的优化设计方法对于多级渣土边坡坡形设计同样适用,且可推广到在起伏不平的渣土受纳场的地形环境进行多级渣土坡形优化设计,对实际的渣土边坡填筑工程具有一定的指导意义。
(4)本文的渣土边坡优化设计方法,未考虑暴雨以及地震等外部诱发因素对边坡稳定性的影响,后续将进一步深入研究。
