基于Massflow模型的西藏仁布杰仲沟泥石流运动特征分析
2020-01-09段学良马凤山孙琪皓
段学良,马凤山,郭 捷,孙琪皓
(1.中国科学院地质与地球物理研究所中国科学院页岩气与地质工程重点实验室,北京 100029;2.中国科学院地球科学研究院,北京 100029;3.中国科学院大学,北京 100049)
0 前言
泥石流是山区发育的一种自然地质现象,泥石流具有突然性以及流速快,流量大,物质容量大和破坏力强等特点[1-3]。发生泥石流常常会冲毁公路铁路等交通设施甚至村镇等,造成巨大损失。2018年7月15日,在距离研究区20 km的G318国道西藏日喀则市仁布段4 739 km+200 m处发生泥石流灾害,导致交通中断,并造成经济损失。所以,对泥石流灾害进行模拟分析,并预测泥石流的流动距离和泛滥范围,从而提出防治措施,对于研究区内的国道通行以及人员安全有着重要的意义。
一般研究泥石流的方法是基于水源、物源、流通条件区域调查数据的统计评价和动力分析方法,这种方式结果可信度高,但耗费大、操作繁琐,经过参数校正的数值模拟也可以提供合理的分析,且成本低廉,是一种重要的研究方式[4]。因此,通过数值分析方法建立泥石流的数值模型,对泥石流的启动过程、流动过程和堆积过程进行模拟,得到的结果借助数据、图形等方式将泥石流的运动过程呈现出来,能够为泥石流灾害防治规划和设计作为参考[5-7]。胡明鉴等[8]利用二维颗粒流程序(PFC2D)分析了降雨作用下松散碎屑物质启动形成泥石流的过程。王纯祥等[9]采用基于GIS的深度积分的二维数值模型,模拟了泥石流的运动规律。HUNGR等[10]使用基于半经验方法和等效流体的DAN3D模型模拟了泥石流的运动过程。Peng等、Chang等、杨涛等使用基于有限差分原理的FLO-2D 模型对泥石流进行模拟,并进行了危险性评价[11-13]。
SAVAGE等[14]提出了基于深度积分的连续介质力学模型,并利用该模型成功模拟了干性沙土的流动过程。该模型的优势是简化了Navier-Stokes模型,大大降低了方程的求解难度,有效地提高了计算效率[15]。OUYANG等提出了基于深度积分的Massflow 数值分析方法,并利用Massflow 软件对滑坡、泥石流等地质灾害进行了数值模拟,不仅很好吻合理论解和实验结果,而且还原了真实灾害的发生过程[16-18]。
以往研究,虽然在整个流域范围内对泥石流进行了分析或评价,但选取的DEM精度都较低,因此不能精细的刻画泥石流的运动规律。为探明研究区流域上游的潜在物源在极端条件下发生泥石流灾害,对沟口建筑及公路的影响,本研究利用无人机技术获取研究区的高精度DEM数据。并采用基于泥石流运动深度积分的Massflow数值分析方法模拟了杰仲沟泥石流的运动过程。
1 研究区地质特征
研究区杰仲沟位于西藏自治区日喀则市仁布县西北方向16 km处(图1),G318国道从沟口穿过,地理位置为东经89°41′10″~89°43′30″,北纬29°16′00″~29°19′27″,属于深切构造高中山地形,流域总体呈树叶状,呈南北向展布,表现为南高北低形态。杰仲沟流域长约6 km,平均宽约0.3 km,汇水面积约27 km2。杰仲沟流域最高点海拔5 394 m,沟口海拔3 794 m,相对高差1 600 m,流域平均纵坡306‰,流域地貌深切,呈“U”型宽谷,沟谷两侧斜坡坡度多在30°左右,物源区坡度约30°。雅鲁藏布江由西向东从堆积区上切过。
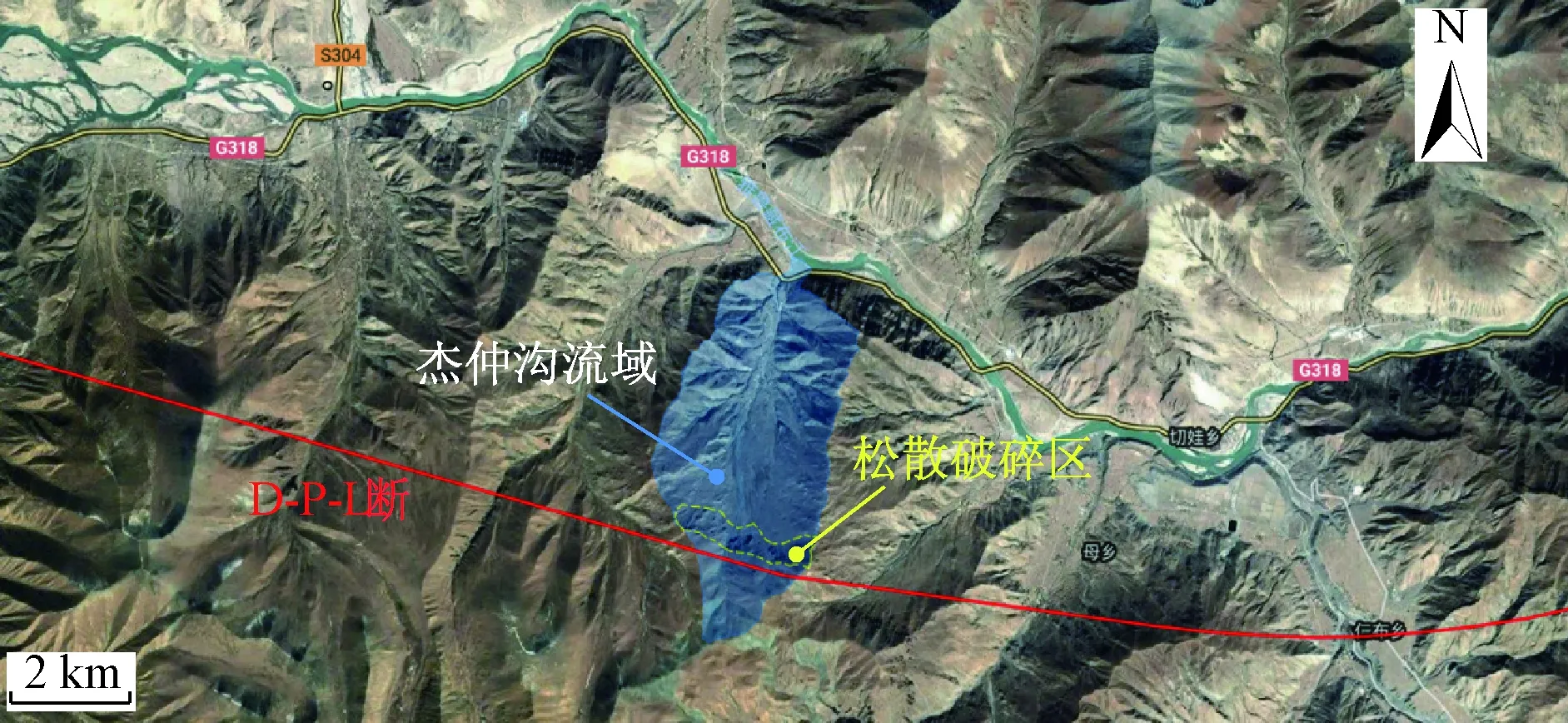
图1 研究区及断裂位置分布Fig.1 The location of the study area and the distribution of the fault
泥石流流域内主要分布紫红、灰色砾岩、砂岩、页岩夹凝灰岩。区域内活动构造发育,主要受第四系活动断裂达机翁-彭错林-朗县断裂影响较大。仁布县属于地震强烈活动区,杰仲沟的地震峰值加速度为0.2g,对应的地震基本烈度为Ⅷ度。仁布县属于温带半干旱高原季风气候,年平均降水量450 mm,雨季集中在7、8月份,降水量占全年的95%。在雨季尤其是暴雨时期,研究区内会增加大量的崩塌、滑坡现象,为泥石流提供了松散固体物源。
2 泥石流形成条件
2.1 地形地貌条件
杰仲沟泥石流流域属于深切构造高中山地貌,相对高差1 600 m。上游形成区地形三面环山,出口为漏斗状,地形比较开阔,周围山高坡陡、植被生长不良,这样的地形有利于降雨的汇集。流通区狭长,沟谷纵坡降大,为松散固体物质参与泥石流活动提供了有利条件。下游堆积区的地形为开阔平坦的河谷。较大的高差和汇水面积使得雨水快速而大量汇集,并侵蚀地表和带动松散固体物质的运动,从而极易引发泥石流的形成。
2.2 物源条件
研究区地质构造复杂,区内地震烈度较高,且发育有新构造断裂,如图1所示的达机翁-彭错林-朗县断裂从研究区穿过(在图1中简称为D-P-L断裂)。流通区沟道两侧的坡体上未发现有大量的破碎松散体,流域内主要松散体物源位于上游的构造断裂附近(图2),在强烈的构造作用下, 岩石裂隙发育, 岩体破碎,同时研究区地处高寒山区,冬季长,气温差异较大,尤其是在春融季节早晚温差更大,加之植被稀少,使基岩的物理以及化学风化作用强烈。长期积累的松散固体物质储量大, 分布集中, 有利于泥石流的补给。

图2 杰仲沟流域全貌Fig.2 The panoramic of Jiezhonggou watershed
2.3 水源条件
研究区年平均降雨量450 mm,7、8月份降雨最为集中,降水量占年降水量的95%, 大雨、暴雨出现频率较高, 加之气温升高, 上游的冰雪消融, 泥石流活动频率, 规模随之增大, 9月降水逐渐减少, 泥石流活动进入低潮期。总的来说,冬春季节降水量少,夏季降水多,丰富的降雨为泥石流的形成提供了水源和动力条件。
3 Massflow 模型
3.1 模型控制方程
对流体动力学三维Navier-Stokes方程进行深度积分,推导出质量和动量控制方程。深度积分是指将控制方程中的各种变量沿深度方向进行积分,这里将对质量守恒方程和动量守恒方程进行深度积分,再运用莱布尼兹法则和动力学边界条件对方程化简,最终得到控制方程如下,公式(1)为质量守恒方程,公式(2)、(3)为动量守恒方程。
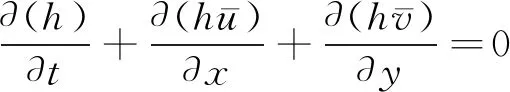
(1)
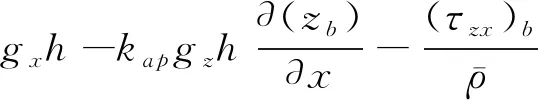
(2)
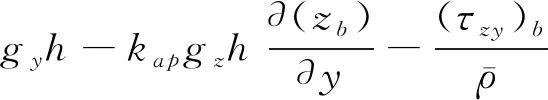
(3)
式中:ρ——流体密度/(kg·m-3);
t——时间;
u,v——x方向和y方向上的流体速度(m/s);
gx,gy,gz——各坐标轴上的重力分量;
Zb——河床标高(m);
h——泥石流体的泥深(m);
τb——底部的剪应力(Pa);
kap——土压力系数。
Massflow 在控制方程的求解方面采用MacCormack-TVD 有限差分法。有限差分法在离散点上直接用差分代替微分,相比于有限元法以及有限体积法的优点是更加简单成熟及可以构造高精度格式,其数值方法具体介绍见文献[16]。
3.2 模型参数选取
3.2.1地形条件
以实地无人机拍摄的照片数据为基础(拍摄区域如图2中的红色阴影所示),建立数字高程模型(DEM),进而生成研究区的地形信息。首先,利用摄影三维建模软件PhotoScan,把研究区的无人机航拍照片进行分析处理,并生成研究区的DEM数据(分辨率为1 m)。然后,运用GlobalMapper、Surfer软件,对DEM数据文件进行裁剪、生成矢量格式等操作,得到流域和物源坐标及高程信息的栅格数据。最后,利用ArcGIS将得到的流域和物源的栅格数据投影,并转换为Massflow软件能识别的ASCⅡ文件格式。
3.2.2物源条件
在流域的上游存在松散破碎区,如图2中黄色虚线所圈的区域。由前文分析可知,该破碎区是一个潜在的泥石流物源,在极端条件下如暴雨、地震等,发生泥石流的概率较高。通过在地图上测量,得到潜在物源区的面积约为6×105m2。
3.2.3泥石流的运动条件
根据现场实地调查,并参考相关研究[19],本模拟选取泥石流容重为1 800 kg/m3。考虑到本模拟中,流体的初始运动位置不是实际的起点位置。因此,通过在低精度DEM(30 m分辨率)的条件下进行模拟,估算出流体的初始速度为10 m/s,所以在进行高精度DEM模拟时,给流体赋一个沿主沟方向的大小为10 m/s的初速度。
分别选用Manning模型和Voellmy摩擦模型,进行初步模拟计算,以选取适用于该研究区的摩擦模型和相应的运动参数。
(1)Voellmy模型
对于Voellmy模型在库伦摩擦模型的基础上增加了湍流项,认为运动的流体受到的抗剪应力为流体所受摩擦力和湍流流动产生的额外阻力之和,因此该模型由摩擦项和湍流项两部分组成,需确定摩擦系数和湍流系数,其表达式如下:
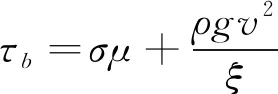
(4)
式中:τb——底部的剪应力/Pa;
σ——正应力/Pa;
μ——摩擦系数;
ρ——泥石流容重/(kg·m-3);
ξ湍流系数/(m·s-2)。
根据相关研究[20]并结合现场调查情况,将摩擦系数μ设定为0.1~0.3,湍流系数ξ设定为150~250 m/ s2。
(2)Manning模型
对于Manning模型,需要确定的计算参数是基底糙率即曼宁系数。本研究根据王裕宜等[21]提出的不同阻力介质状态下统一的阻力糙率系数表征公式计算,公式如下:
nc=0.033Rns-0.51exp(0.34Rns0.17)lnh
(5)
式中:nc——曼宁系数;
Rns——泥砂比;
h——泥深/m。
根据现场调查情况,取Rns=0.75,h为2~10 m,代入公式(4)得到杰仲沟的曼宁系数取值范围0.04~0.12。
为了选取适于杰仲沟泥石流数值模拟的摩擦模型和相应运动参数,对两种摩擦模型Voellmy和Manning模型分别设定不同的运动参数,得到了不同的泥石流泥深、流动强度以及堆积范围,对比已发生的泥石流,选择与实际情况最匹配的模型及运动参数。对于Voellmy模型将摩擦系数μ设定在0.1~0.3,湍流系数ξ设定为150~250 m/ s2。对于Manning模型,将曼宁系数设定在0.04~0.12。泥石流容重取1 800 kg/m3,流体体积取6×104m3。对比不同运动参数的模拟结果,最终选取μ=0.1,ξ=200 m/s2,nc=0.08。如图3和图4分别是Voellmy模型和Manning模型的模拟结果。
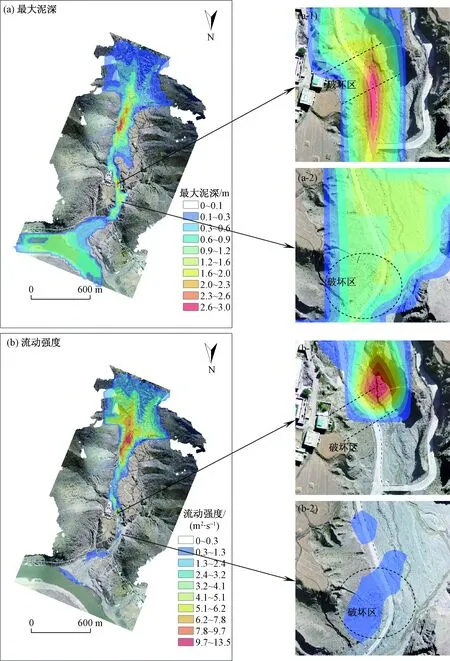
图3 泥石流最大泥深和流动强度分布, Voellmy模型Fig.3 Maximum depth and flow intensity distribution of the debris flow, Voellmy model
图3(a)和图4(a)分别是两种模型整个运动过程中最大泥深的分布,图3(b)和图4(b)是最大泥深与泥石流运动速度的乘积,代表了泥石流的流动强度。从泥深分布图中可以看出,两种模型的泥石流的堆积范围模拟结果与实际已发生的泥石流几乎相同,但是Manning模型的模拟结果更接近实际情况,而Voellmy模型模拟的泥石流运动范围误差相对较大,尤其在流通区内。同样在流动强度分布图中也可看出,Manning模型比Voellmy模型的模拟结果更精确。虽然两种模型在精度上有一定差距,但是总的规律是相同的。图3和图4的(a-1)和(a-2)是实际被泥石流冲毁的两处公路石墩护栏。图3、图4的(a-1)中的两条黑色虚线之间的公路西侧的石墩护栏被冲毁,(a-2)中被黑色虚线圈起的公路西侧的石墩护栏也被冲毁。两种模型的模拟结果都与实际情况相匹配,尤其是Manning模型,从这两个图中可以看出,泥深在这两处都达到了4 m左右,这说明模拟结果与实际匹配的较好。此外,在图4(b)泥石流流动强度分布图中可以看出,泥石流初始运动阶段流动强度迅速增大,随后逐渐减小,但是在上述两处石墩护栏冲毁处,流动强度表现为增大。因此,也与实际情况匹配良好,这说明所选取的运动参数能够较真实的描述研究区内泥石流的运动状态。综合比较上述两种摩擦模型,最终选取Manning模型对该泥石流沟做进一步的模拟研究。

图4 泥石流最大泥深和流动强度分布,Manning模型Fig.4 Maximum depth and flow intensity distribution of the debris flow, Manning model
4 模拟结果
根据估算的流域上游存在1.0×105~6.0×105m3的固体物源,考虑到运动过程中流体的损失量,本次模拟选取流体体积为3.0×105m3。利用已选模型和相应参数对此体积的泥石流运动进行模拟,并分析其影响范围和危险性。
此次模拟共进行了600 s。如图5和图6分别是不同时刻的泥深分布图和整个泥石流运动过程中最大泥深及流动强度的分布图。可以看出泥石流刚开始运动30 s最大泥深就达到了6 m,90 s时达到了8 m,且流动速度快,已达到甘丹桑阿曲林寺前,此后流动速度变慢,并出现堆积。这是因为甘丹桑阿曲林寺南侧的沟道较为平直,而在寺前以及其北侧,沟道出现了两次较大的弯曲,从而使流体速度减慢并发生堆积。模拟计算进行到180 s时,泥石流体穿过了沟口处的G318国道,并开始扩散流入堆积区。进行到270 s时,泥石流体开始流入雅江,并在寺北侧第二个弯道处发生堆积回流,流入西侧的支沟中。450 s时,大部分流体流进雅江,最大泥深减小到4 m,600 s时泥石流运动基本结束。此次模拟,整个泥石流运动过程中出现的最大泥深高达9.6 m。
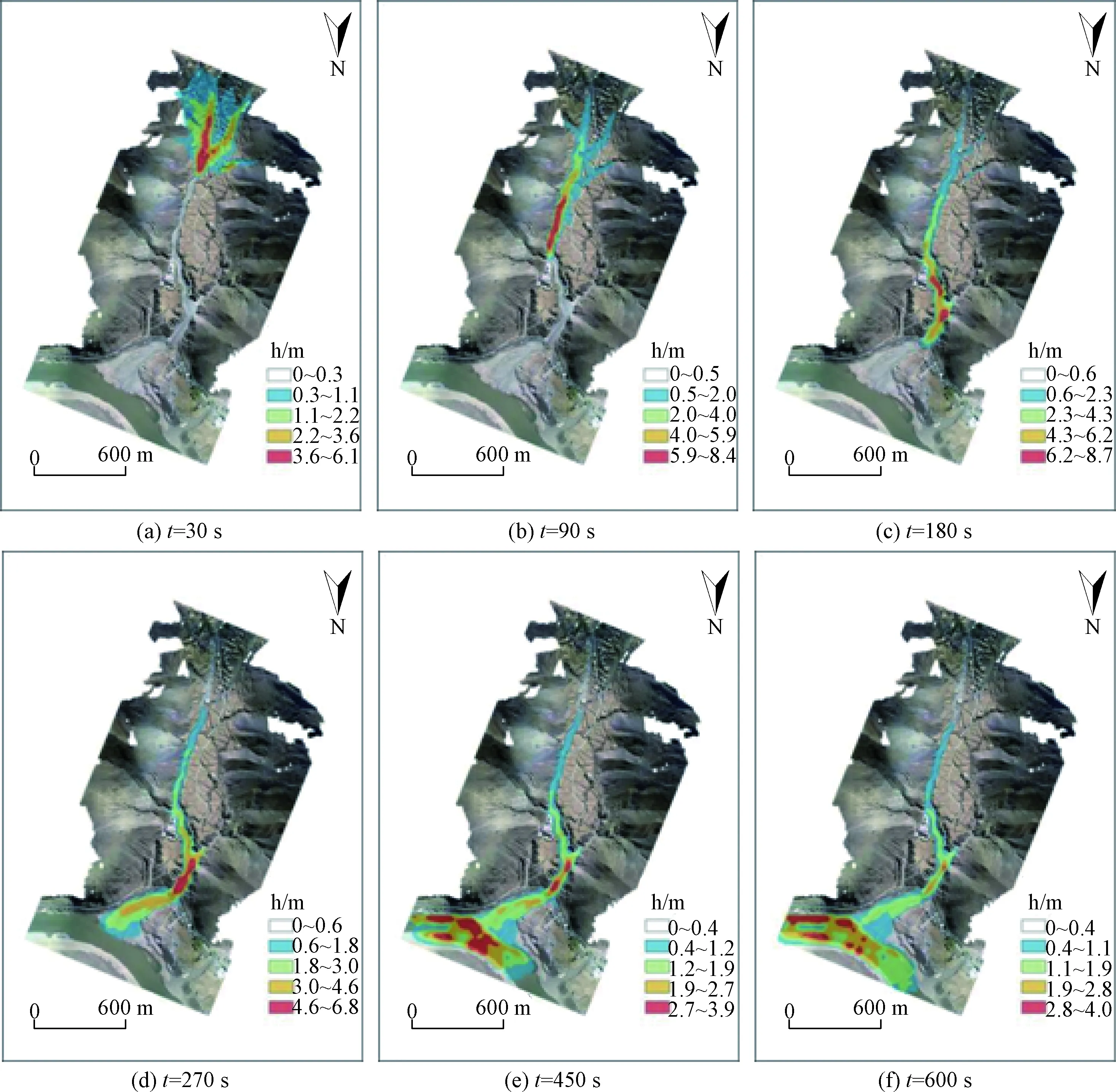
图5 不同时刻的泥深分布Fig.5 Mud depth distribution of debris flow at different times
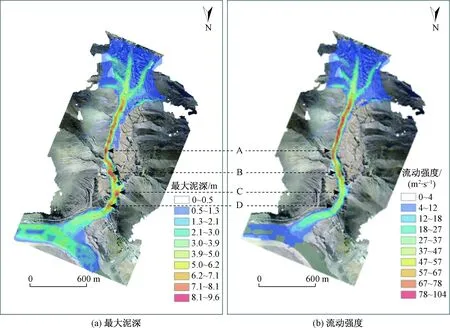
图6 泥石流最大泥深和流动强度分布Fig.6 Maximum depth and flow intensity distribution of the debris flow
综合最大泥深和流动强度分布图,定义了研究区内四处危险区,分别在图6中标为A、B、C、D,图7是其放大图。最大泥深出现在图6(a)中的A和B处,A处在沟道第一个弯道前,流体进入弯道后流速减小,发生堆积;B处是石墩护栏被冲毁的地点,此处位于两个弯道之间,所以泥石流也易在此堆积;另一个护栏被冲毁的地点C处位于第二个弯道处,最大泥深达到了8.7 m。G318国道南侧沟道D处的最大泥深为7.8 m,国道上的最大泥深达到了5 m。此次模拟中,流动强度的最大值为104 m2/s,流动强度大的区域集中在第一个弯道南侧,即A处以南,这部分区域中沟道较为平直,泥石流流速快,冲击力强,但A处之后流动强度有所减小,但在B处,流动强度再次出现一个较大值,达到了75 m2/s,在B处危险区边缘有一通向上游村庄的公路,从泥石流沟上架桥而过。G318国道处,达到36 m2/s,泥石流穿过国道后流入堆积区,流动强度逐渐减小。
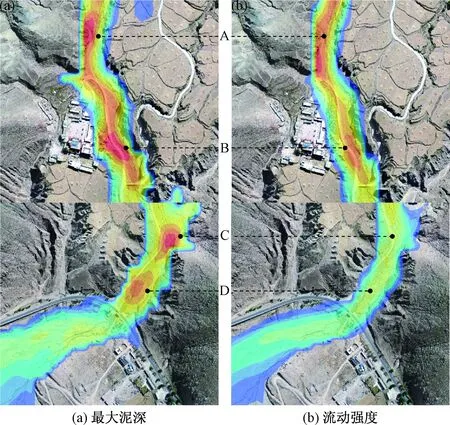
图7 危险区放大图Fig.7 Enlarged map of risk zones
5 结论
对实际已发生的泥石流进行了数值模拟,模拟结果与实际情况匹配良好,从而确定了适合研究区杰仲沟泥石流模拟的摩擦模型和运动参数。
在选取了摩擦模型和相应运动参数的基础上,又对可能发生的更大体积的泥石流灾害进行了模拟,对泥石流从发生到休止,整个动态过程进行了分析。主要描述了不同时刻的泥深分布情况,以及对整个运动过程中的最大泥深分布和流动强度分布进行了分析,并划定了研究区内的四处危险区,从而得出以下结论。
(1)泥深和泥石流流动强度较大的区域,主要分布危险区A及以南的区域,即沟道第一个弯道南部,但处于这一范围的大部分区域人类活动较少,仅在弯道处有一条通向寺庙的公路。
(2)危险区B在泥石流沟的第一个弯道与第二个弯道之间,危险区C在第二个弯道处,并且这两处的模拟结果与实际情况较为符合,公路旁的石墩护栏被泥石流冲毁,并且危险区B内有一通向上游村庄的公路,从泥石流沟上架桥而过。因此,在地震(地震烈度为Ⅷ度)和极端气候条件如暴雨的情况下,这两个区域的危险性相对较高,需对其加强防护。
(3)G318国道在沟口穿过,危险区D位于国道南侧附近,虽然流动强度相对其他危险区不大,但是流体在这个区域容易发生堆积,最大泥深达到了7.8 m。因此,大量堆积的泥砂、石块等容易造成对国道的冲埋,严重影响交通通行。所以,应提高此处公路下涵洞的排导能力,预防灾害的发生。
