基于AHP法的景观亭综合评价指标体系研究★

陈文彬 陈丽晖

(肇庆学院生命科学学院，广东 肇庆 526061)

景观亭是风景园林中常见的一种小型建筑形式，具有观赏性、文化性及实用性，对景区景观营造质量具有重要意义。但是，目前国内对景观亭的评价仍然处于定性描述阶段，尚未有一套科学合理的综合评价系统。层次分析法(Analytic Hierarchy Process,AHP)是对定性问题进行定量分析的一种简便、灵活而又实用的多准则决策方法[1]。其特点是对复杂问题的本质、影响因素及其内在关系等进行深入分析，利用较少的定量信息使形成决策的过程数学化，为多目标、多准则或无结构特性的难于完全定量的复杂问题提供简便的决策方法。本研究拟借鉴国内外的相关成果[2-4]，采用AHP法构建出一套科学可靠的景观亭综合评价指标体系，以期为景观亭以及其他景观建筑的综合评价及开发利用提供借鉴与参考。

1 研究方法

1.1 评价指标体系的建立与指标选取

评价指标选取的合理性对评价结果的准确性与科学性有最直接的影响。景观亭具有观赏价值、文化价值与实用价值等三方面的价值。为达到客观合理地对景观亭进行评价的目的，通过查阅专业文献及专家咨询法建立评价体系并确立相关指标。即参考国内外相关景观评价体系研究的专业文献[5-15]以及各种大型园林景观评价指标，构建出景观亭综合评价指标体系并初拟55条具体的指标向风景园林专家组成员进行多轮征询和反馈，筛选出39个最具有代表性的指标。

景观亭评价指标体系具体如下：第1层为目标层，即景观亭评价指标体系；第2层为项目层，包含景观亭的观赏价值、文化价值与实用价值3个层次功能；第3层为评价因素层，即每一个评价准则具体由哪些因素决定，共15个因素；第4层为指标层。其中观赏价值包括造型美、远景美、近观美、赏景美、配色美、植物配置美、细部装饰美、感官体验美；文化价值包括历史人文价值、楹联牌匾点景、诗画意境；实用价值包括环境协调性、选址合理性、亭内空间合理性、结构合理性。共3个项目层，15个因素层及39个指标层，从多因素多角度对景观亭进行综合评价。

1.2 指标权重的确定

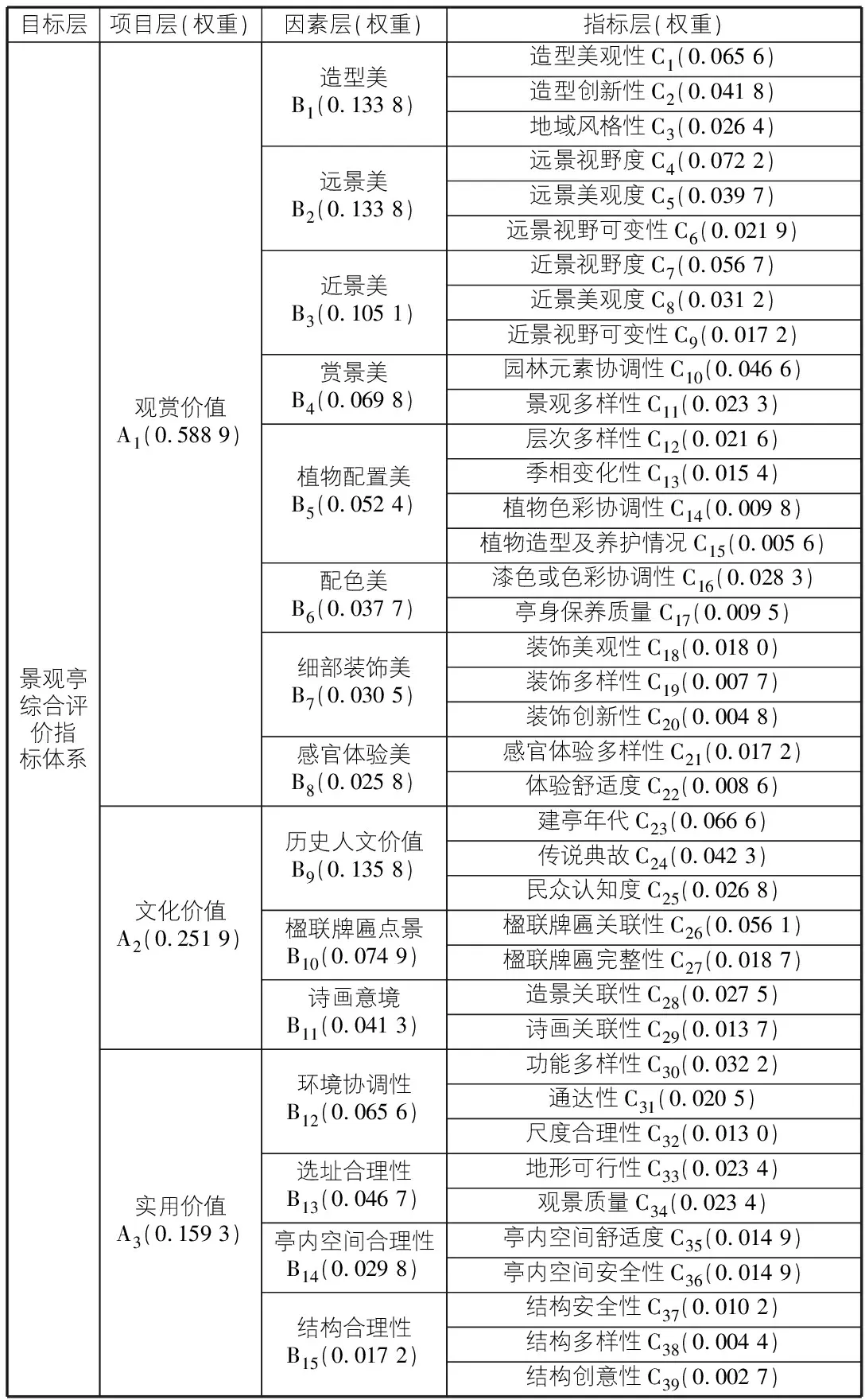
表1 景观亭综合评价体系

通过专家咨询法，对上述确立的评价指标体系中的项目层、因素层、指标层各要素的重要性初步进行排序。趋向一个比较可靠、一致的结论。同时通过对七星岩景区游客的问卷，了解游客对景观亭项目层、因素层重要性的认知与排序，并与专家的初步排序进行对照比较，分析专家与普通游客认知度的差异。如差异不大，说明既定评价指标体系较合理、科学，不需要改动；如差异较大，则向专家反馈意见，供最终确定指标体系与权重作参考(最终指标体系构成与权重参见表1)。

1.3 游客问卷设计

对七星岩景区的游客发放关于景观亭评价重要性认知的问卷，由于指标层相对细化且专业性较高，所以问卷中只调查项目层与因素层重要性认知。共发放300份，收回有效问卷266份，其中男女比例分别为47.37%和52.63%。主要调查内容包括：1)是否同意景观亭的价值包括观赏价值、文化价值、实用价值3个方面以及三者重要性的排序；2)是否同意观赏价值由造型美、近景美、远景美、赏景美、细部装饰美、配色美、感官体验美、植物配置美等8个指标构成以及指标间重要性的排序；3)是否同意文化价值方面包含以建亭年限、诗画意境表达、楹联牌匾点景等3个指标以及指标间重要性的排序；4)是否同意实用价值方面包含环境空间规划协调性、选址合理性、亭内空间合理性、结构合理性等4个指标以及指标间重要性的排序。

1.4 问卷结果

提取答卷中赞同人数最多的观点，其结果与专家组观点相同。权重排序中赞同项目层重要性：A1>A2>A3的人数占比97.37%，赞同因素层1重要性排序为B1>B2>B3>B4>B5>B6>B7>B8的占比98.87%，赞同因素层2重要性排序为B9>B10>B11的占比98.87%，赞同因素层3重要性排序为B12>B13>B14>B15占比98.12%。

2 计算方法与过程

2.1 建立判断矩阵

基于专家评定与问卷结果的初步权重排序，进行各指标对比矩阵的建立。

2.2 最大特征值和特征向量计算

通过METLAB软件求解判断矩阵的最大特征值为λmax，其对应的特征向量为ω，将列向量归一化后得到该层元素相对于上层次某一因素的相对权重值，即层次单排序。将元素单层排序权重乘以其对应的上一层元素的单排序权重即得该指标的总排序权重值[15]。B层对A层的权重WBi(i=1,2,3)；C层对B层的权重值WCi(i=1,2,3,…,15)；D层对C层的权重值WDi(i=1,2,3,…,39)；D层对A层的权重值tDi=WBi·WCi·WDi(i=1,2,3,…,39)。

一致性检验:

为确保结论的可靠性与合理性，对各判断矩阵进行一致性检验[15]，如式(1),式(2)。检验该系统成对比较矩阵B或Ci一致性的步骤如下：

计算衡量各个成对比较矩阵B或Ci(n>1阶方阵)不一致程度的指标CI：

CI=(λmax-n)/(n-1)

(1)

因为一致性的偏差可能是由于随机因数导致的，因此在检验判断矩阵是否具有满意的一致性时，还需将CI和随机一致性指标RI进行比较，得出检验系数CR，公式如下：

CR=CI/RI

(2)

如果CR<0.1，则认为该判断矩阵通过一致性检验，否则就不具有满意一致性[15]。

2.3 计算结果分析

2.3.1一致性检验结果

通过一致性的计算结果，得出各判断矩阵的不一致程度的指标CI均小于0.1(包括15个指标层判断矩阵)，证明其具有满意一致性，说明层次分析法所计算的景观亭多维评分系统的各指标的权重值是科学可靠的，计算的相应评分可作为该指标的最终分数(参见表2)。

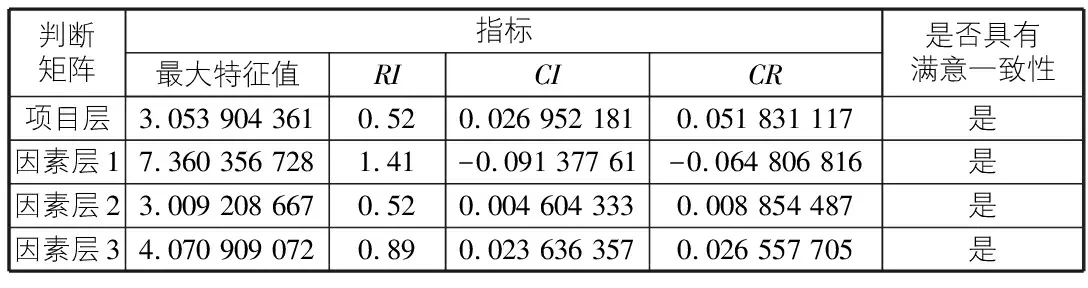
表2 判断矩阵一致性检验结果

2.3.2权重计算结果

权重分配见图1，图2。

3 景观亭综合评价与应用测试

3.1 景观亭综合评分及等级确定

依据39个指标对所要评价的景观亭进行打分，采用五段评分法。即：优异(0.8～1)，良好(0.6～0.8)，一般(0.4～0.6)，较差(0.2～0.4)，差(0～0.2)，得到各指标的评价分并依据各指标所占权重，计算出各指标的加权分。各因素层的加权分为其相应指标层加权分之和，评价分则通过加权分除以其相应权重换算。同理，获得各项目层加权分及评价分。3个项目层加权分之和即为该景观亭的综合评分，对照分级标准确定该景观亭的综合评价等级。综合评价等级标准：优异(0.8～1)、良好(0.6～0.8)、一般(0.4～0.6)、较差(0.2～0.4)、差(0～0.2)。

3.2 评价体系应用检测

项目组依据上述建立的景观亭综合评价体系对七星岩濯缨亭的各项指标进行评价。项目层的评价结果是：观赏价值(0.654 3)>实用价值(0.593 8)>文化价值(0.583 9)，观赏价值的评价分最高，达到良好等级，实用价值与文化价值亦接近良好，综合分为0.627 1，综合评价等级为良好。结合实际分析，濯缨亭为一桥亭，于1978年建于七星岩景区红莲湖曲桥最低处，湖面宽淼，亭身古朴，伫立水中，曲桥如玉带，与远处群山岸树相映，无论远景近景构图都很美，远视尤佳。濯缨亭亭身低于桥高，水面涨起时水稍稍浸过亭基，取屈原诗“沧浪之水清兮,可以灌吾缨,沧浪之水浊兮,可以灌吾足”，意指水清可洗衣帽，水浊唯可清足，隐喻天下安定可大展才华，天下动乱便韬光养晦、独善其身，故名“濯缨亭”。该亭选址适宜，构图优美，功能独特，且引用了历史典故丰富了景观亭的内涵，提高了游客的游玩体验，成为七星岩景区一处较为知名和游客喜爱的景观亭。经由本综合评价指标体系的评测结果与游客体验基本一致，说明该评价体系具有一定的科学性与应用价值(见图3，表3)。

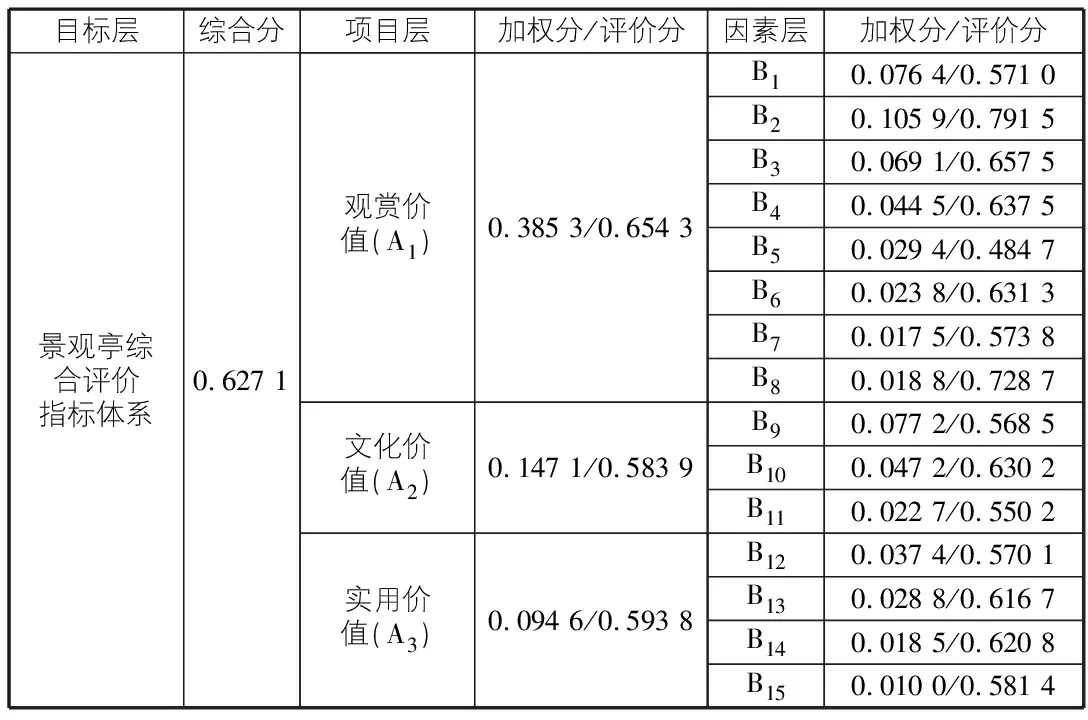
表3 濯缨亭评价结果

4 讨论

本项目组基于AHP法结合专家咨询法与问卷调查，从景观亭观赏价值、文化价值、实用价值(项目层)着手，通过深入调查研究分析，确立了15个因素层与其下属的39个指标层的权重，涵盖了直观感受、内在文化内涵以及更深层次的精神感受等多方面内容，构建出具有一套综合科学实用的景观亭综合评价指标体系。从三大项目层指标的权重排序可知，观赏价值(0.588 9)≫文化价值(0.251 9)>实用价值(0.159 3)，可见在景观亭的评价或建设中，其观赏价值应是主要考虑的因素，景观亭规划设计首先应从观赏性上出发，创设美的、吸引度高的景观亭欣赏境域。而人们的观赏体验又不是单一的，而是包括了造型、装饰、配色、植物配置以及远景、近景及在景观亭内的赏景体验等诸多因素。因此，在景观规划设计中应综合考虑人们对景观建筑的欣赏体验并注重整体感受，对景观建筑的观赏价值评价也应综合全面。此外，文化价值与实用价值也不容忽视。文化价值是美学价值的内在价值表现，文化底蕴的加持能提升景观的韵味和增加意境的内涵。此外，景观亭还具遮阴、避雨、休憩等其他实用功能，是人们放松、赏景、娱乐的良场，在规划设计与评价中，景观亭的实用价值也值得我们重视。应结合以人为本、因地制宜的原则，在景观亭的设计与选址中做到观赏性、文化性与实用性的有机结合。

景观亭综合指标综合评价体系的确立，依据以人为本的原则，从人文、美学、生态等多方面进行客观而综合的评估，使体系更为完善与科学合理，为风景园林景观建筑的评价研究提供了新的思路与方法，亦可为今后景观建筑的规划设计提供一定的参考借鉴。本指标综合评价系统比较适合应用于中式景观亭或文化追求和建筑构造与中国相似的日式景观亭的评价。考虑到中外建筑在制作方法、造型结构与审美文化追求方面的差异，对西式景观亭指标层因素层及指标层的具体指标如楹联牌匾点景等可作相应的修改或删除。其他景观建筑的综合评价系统亦可以本系统作为借鉴参考。另外，本评价系统有39个具体的评价指标，稍嫌过于细化和繁琐，可作进一步简化和完善。

致谢：本项目得到邱晓君、夏蕊梅、莫家杰、杨秀娴、蔡艺、陈熙臻、冼宇杰等同学的大力支持。特此致谢！